Pertemuan 3 BAHASA REGULAR Bahasa Reguler 1 PENDAHULUAN

Pertemuan 3 BAHASA REGULAR Bahasa Reguler 1

PENDAHULUAN n n Sebuah bahasa dinyatakan regular jika terdapat finite state automata (FSA) yang dapat menerimanya. Bahasa-bahasa yang diterima oleh FSA bisa dinyatakan secara sederhana dengan ekspresi regular (regular expression). Ekspresi regular memberikan suatu pola (pattern) atau template untuk untai/string dari suatu bahasa. Banyak masalah pada perangkat lunak yang bisa disederhanakan dengan melakukan pengubahan notasi ekspresi regular ke dalam implementasi komputer dari FSA yang bersangkutan. Bahasa Reguler 2

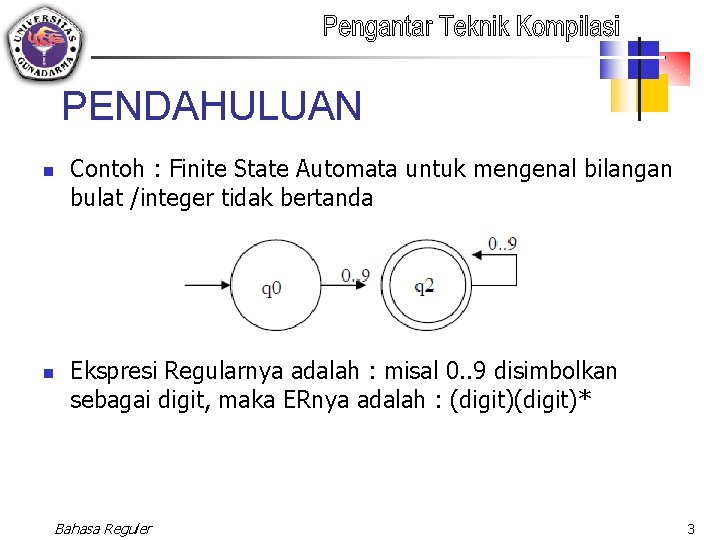
PENDAHULUAN n n Contoh : Finite State Automata untuk mengenal bilangan bulat /integer tidak bertanda Ekspresi Regularnya adalah : misal 0. . 9 disimbolkan sebagai digit, maka ERnya adalah : (digit)* Bahasa Reguler 3

PENDAHULUAN n n Bahasa regular adalah penyusun ekspresi reguler (ER) Ekspresi reguler terdiri dari kombinasi simbol-simbol atomik menggunakan 3 operasi yaitu : – katenasi, – alternasi, dan – repetisi /closure n n Pada kasus scanner, simbol-simbol atomik adalah karakter-karakter di dalam program sumber. Dua buah ekspresi regular adalah ekuivalen jika keduanya menyatakan bahasa yang sama Bahasa Reguler 4

NOTASI EKSPRESI REGULAR n n Supescript * : berarti bisa tidak muncul, bisa juga muncul berhingga kali (0 -n) Superscript + : berarti minimal muncul satu kali (1 -n) + : berarti union atau bisa diganti dengan notasi U. : berarti konkatenasi, biasanya tanpa ditulis titiknya, misal ab sama dengan a. b Bahasa Reguler 5

Operasi Regular - katenasi n Katenasi /konkatenasi atau sequencing disajikan dengan physical adjacency - e. g. ekspresi regular ‘<letter> <digit>’ bentuk penyajian sederhana (diasumsikan sebagai definisi yang jelas dari letter dan digit) komposisi terurut dari letter diikuti dengan digit - “<” dan “>” digunakan untuk mengidentifikasi simbol-simbol yang merepresentasikan simbol spesifik (menggunakan ekspresi regular) - Kita bisa menggunakan “: : =” (ekivalensi) untuk menggabungkan ekspresi regular yang didefinisikan dengan <letter> dan <digit> Bahasa Reguler 6

Operasi Regular - katenasi n Concatenation adalah penyambungan dua buah string. Diberikan dua string : x = abc, dan y = 123 Contoh : concate(xy) = x. y = xy = abc 123 , x. ε = x = abc A = {cat, dog} dan B {house}, maka A. B = {cathouse, doghouse} A. (ε) = (ε). A = A bersifat asosiatif : x(yz) = (xy)z Bahasa Reguler 7

Operasi Regular - alternasi n Alternasi membolehkan pilihan dari beberapa pilihan dan biasanya disajikan dengan operator ‘|’ – E. g. <digit> : : = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 » contoh yang menggunakan juga operator ekivalensi n Bentuk tulisan cepat tertentu juga biasanya digunakan dengan alternasi (khususnya ellips) – E. g. <letter> : : = a | b | … | z | A | B | … | Z » Can use the ellipses (“…”) when a sequence is well defined Bahasa Reguler 8

Operasi Regular - alternasi n Alternation adalah pilihan satu di antara dua buah string. Contoh : alternate(xy) = x | y = abc atau 123 Tiga sifat aljabar alternation : ♦ Operasi alternation bersifat komutatif : x | y = y | x ♦ Operasi alternation bersifat asosiatif : x | (y | z) = (x | y) | z ♦ Elemen identitas operasi alternation adalah dirinya sendiri : x | x = x ♦ Sifat distributif concatenation terhadap alternation : x (y | z) = xy | xz Bahasa Reguler 9

Operasi Regular - repetisi n n Terakhir, repetisi membolehkan ekspresi dari kontruksi yang diulang beberapa kali Terdapat 2 operator yang digunakan yaitu superscript ‘+’ dan superscript ‘*’ – E. g. <word> : : = <letter>+ » ini menyatakan sebuah kata terdiri atas satu atau lebih huruf (* akan menyatakan nol atau lebih huruf-huruf dan sebuah kata harus paling sedikit memiliki satu huruf sehingga kita menggunakan +) Bahasa Reguler 10

Ekivalensi/Kesamaan ER [1] Contoh : Perhatikan bahwa kita tidak bisa membuat ekspresi regular dari bahasa atau , karena keduanya tidak dihasilkan dari grammar regular. Reguler Bahasa n 11

Ekivalensi/kesamaan ER[2] (a b)* a = a (b a)* Bukti : (a b)* a = ( (ab) (abab) …) a = ( a(aba) (ababa) …) = (a|(aba)|(ababa)|…) = a ( (ba) (baba) …) = a (b a)* n Bahasa Reguler 12

AUTOMATA HINGGA (AH) n AH didefinisikan sebagai pasangan 5 tupel : (K, , M, S, Z). K : himpunan hingga stata, : himpunan hingga simbol input (alfabet) M : fungsi transisi, menggambarkan transisi stata AH akibat pembacaan simbol input. Fungsi transisi ini biasanya diberikan dalam bentuk tabel. S ∈ K : stata awal Z ⊂ K : himpunan stata penerima Bahasa Reguler 13

AUTOMATA HINGGA (AH) n Ada dua jenis automata hingga : deterministik (AHD, DFA = deterministic finite automata) dan non deterministik (AHN, NFA = non deterministik finite automata). - AHD : transisi stata AH akibat pembacaan sebuah simbol bersifat tertentu. - AHN : transisi stata AH akibat pembacaan sebuah simbol bersifat tak tentu. Bahasa Reguler 14

AUTOMATA HINGGA DETERMINISTIK(AHD) n n Berikut ini sebuah contoh AHD F(K, , M, S, Z), dimana : M diberikan dalam tabel berikut: Bahasa Reguler 15

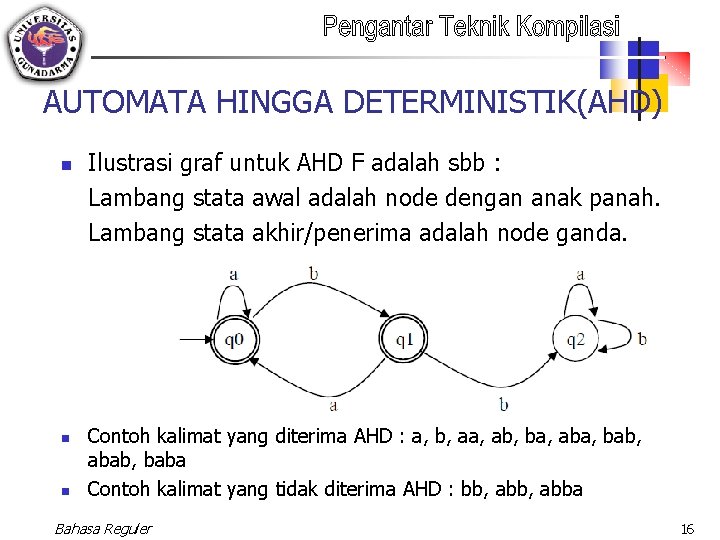
AUTOMATA HINGGA DETERMINISTIK(AHD) n n n Ilustrasi graf untuk AHD F adalah sbb : Lambang stata awal adalah node dengan anak panah. Lambang stata akhir/penerima adalah node ganda. Contoh kalimat yang diterima AHD : a, b, aa, ab, ba, aba, bab, abab, baba Contoh kalimat yang tidak diterima AHD : bb, abba Bahasa Reguler 16

AUTOMATA HINGGA NONDETERMINISTIK(AHN) n n Berikut ini sebuah contoh AHN F(K, , M, S, Z), dimana : M diberikan dalam tabel berikut: Bahasa Reguler 17

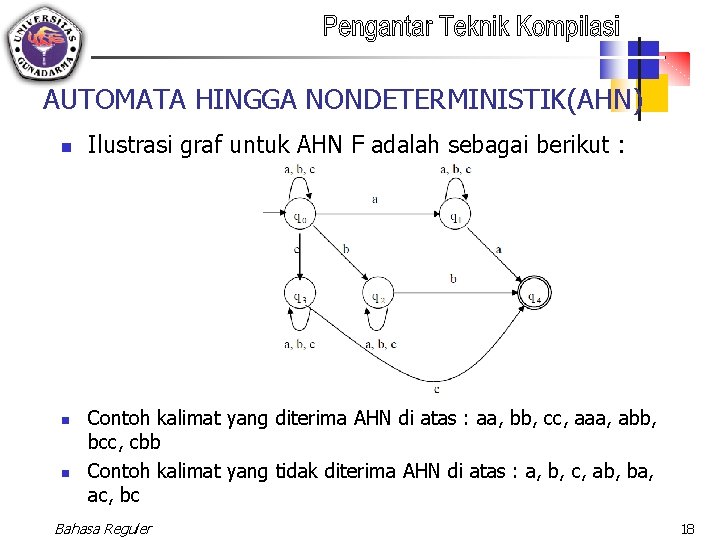
AUTOMATA HINGGA NONDETERMINISTIK(AHN) n n n Ilustrasi graf untuk AHN F adalah sebagai berikut : Contoh kalimat yang diterima AHN di atas : aa, bb, cc, aaa, abb, bcc, cbb Contoh kalimat yang tidak diterima AHN di atas : a, b, c, ab, ba, ac, bc Bahasa Reguler 18

AUTOMATA HINGGA NONDETERMINISTIK(AHN) n n n Sebuah kalimat di terima AHN jika : • salah satu tracing-nya berakhir di stata penerima, atau • himpunan stata setelah membaca string tersebut mengandung stata penerima Contoh : Telusurilah, apakah kalimat-kalimat berikut diterima AHN : ab Himpunan stata tidak mengandung stata penerima ⇒ kalimat ab tidak diterima Bahasa Reguler 19

AHN DENGAN TRANSISI HAMPA n n Perhatikan AHN berikut AHN di atas mengandung ruas dengan bobot ε. AHN demikian dinamakan AHN dengan transisi ε, atau singkatnya AHN-ε di atas menerima bahasa Bahasa Reguler 20

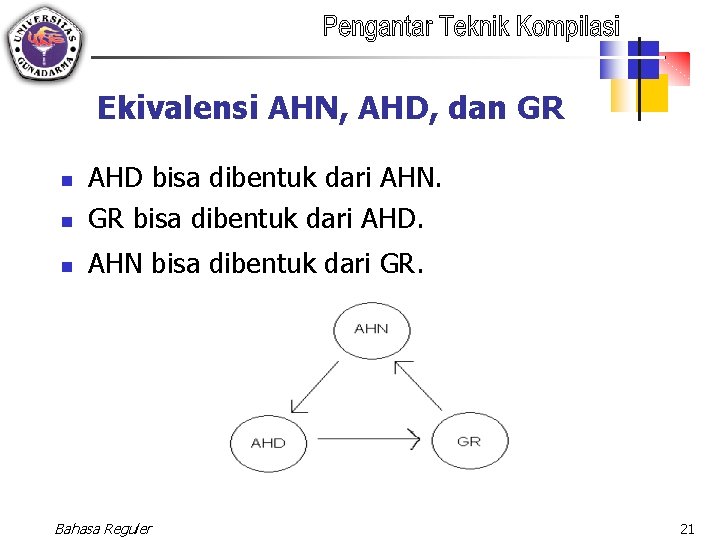
Ekivalensi AHN, AHD, dan GR n AHD bisa dibentuk dari AHN. GR bisa dibentuk dari AHD. n AHN bisa dibentuk dari GR. n Bahasa Reguler 21

Pembentukan AHD dari AHN Diberikan sebuah AHN F = (K, , M, S, Z). Akan dibentuk sebuah AHD F’ = (K’, ’, M’, S’, Z’) dari AHN F tersebut. Algoritma pembentukannya adalah sbb. : 1. Tetapkan : S’ = S dan ’ = 2. Copykan tabel AHN F sebagai tabel AHD F’. Mula-mula K’ = K dan M’ = M 3. Setiap stata q yang merupakan nilai (atau peta) dari fungsi M dan q K, ditetapkan sebagai elemen baru dari K’. Tempatkan q tersebut pada kolom Stata M’, lakukan pemetaan berdasarkan fungsi M 4. Ulangi langkah 3 di atas sampai tidak diperoleh stata baru 5. Elemen Z’ adalah semua stata yang mengandung stata elemen Z. Bahasa Reguler 22

Pembentukan GR dari AHD Diketahui sebuah AHD F = (K, V, M, S, Z). Akan dibentuk GR G = (V’, V, S’, Q). Algoritma pembentukan GR dari AHD adalah sebagai berikut : n Tetapkan V’ = V, S’ = S, V = S n Jika A, A K dan a V, maka : M(A, a) = A ekuivalen dengan produksi : Bahasa Reguler 23

Pembentukan AHN dari GR Diketahui GR G = (V, V, S, Q). Akan dibentuk AHN F = (K, V’, M, S’, Z). Algoritma pembentukan AHN dari GR : n Tetapkan V’ = V, S’ = S, K = V n Produksi A a A ekuivalen dengan M(A, a) = A Produksi A a ekuivalen dengan M(A, a) = X, dimana X V n K = = K {X} n Z = {X} Bahasa Reguler 24

Ekivalensi AHN- Dengan ER (Ekspresi Regular) Bahasa Reguler 25