CSE 3813 Introduction to Formal Languages and Automata

CSE 3813 Introduction to Formal Languages and Automata Chapter 1 Introduction to the Theory of Computation These class notes are based on material from our textbook, An Introduction to Formal Languages and Automata, 4 th ed. , by Peter Linz, published by Jones and Bartlett Publishers, Inc. , Sudbury, MA, 2006. They are intended for classroom use only and are not a substitute for reading the textbook.

Acknowledgement Unless otherwise credited, all class notes on this website are based on the required textbook for this course, Linz, Peter. An Introduction to Formal Languages and Automata, 4 th ed. Sudbury, Mass. : Jones and Bartlett Publishers, 2006. These notes are intended solely for the use of the students in the CS 3813 class at Mississippi State University. Please assume any errors to be mine, and not the author of the textbook.

What does the title of this course mean? • Grammar – A set of rules for generating all and only the strings of a particular language – Example: the grammar (syntax rules) for the C language • Formal language – a subset of the set of all possible strings from a set of symbols – Example: the set of all syntactically correct C programs • Automata – abstract, mathematical model of computer – Examples: finite automata, pushdown automata Turing machine, RAM, PRAM, many others • We will consider each of these in this course

Focus of the course • What are the fundamental capabilities and limitations of computers? • To answer this, we will study abstract mathematical models of computers. • These mathematical models abstract away many of the details of computers to allow us to focus on the essential aspects of computation. • These models also allow us to develop a mathematical theory of computation.

What is computation? • Computation is the execution of an algorithm by a computer. • An algorithm is a sequence of primitive steps that can be specified explicitly. • An algorithm can be performed mechanically, that is, by a machine • It computes a function that transforms input into output.

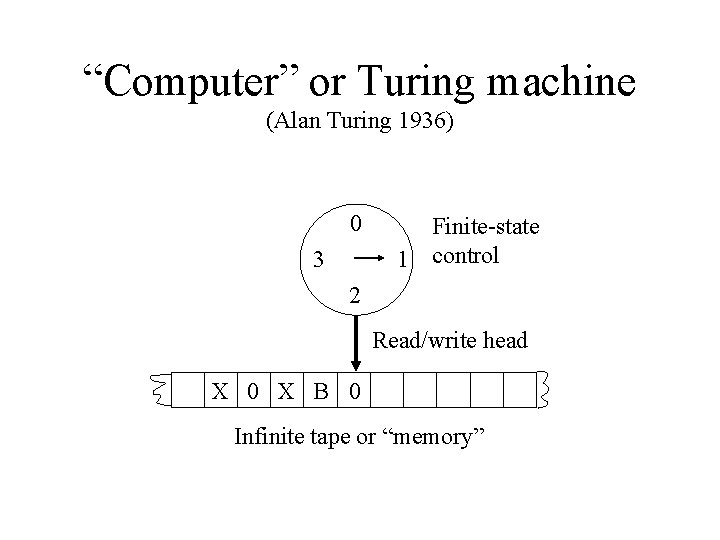
“Computer” or Turing machine (Alan Turing 1936) 0 3 Finite-state 1 control 2 Read/write head X 0 X B 0 Infinite tape or “memory”

Automata • An automaton has: – Input File – Control Unit (with finite states) – Temporary Storage – Output

Finite automata • Developed in 1940’s and 1950’s for neural net models of brain and computer hardware design • Finite memory! • Many applications: – text-editing software: search and replace – many forms of pattern-recognition (including use in WWW search engines) – compilers: recognizing keywords (lexical analysis) – sequential circuit design – software specification and design – communications protocols

Finite automata • For the computer engineers among us, you may think of finite automata as in-line filters. • In an in-line filter, a signal comes in and the filter handles it, depending only upon the signal’s characteristics and the state the filter is in. • The typical in-line filter has no auxiliary memory. • The filter can change its state from one state to another, depending upon the signal it receives. • By being in a different state the next time it receives a given signal, it can handle the same signal in different ways.

Pushdown automata • Noam Chomsky’s work in the 1950’s and 1960’s on grammars for natural languages • infinite memory, organized as a stack • Applications: – compilers: parsing computer programs – programming language design

Turing machine • Devised by Alan Turing • Has infinite memory, organized as a tape, with a read/write head • Most powerful automaton; it can be proven that no computer can be more powerful than a Turing machine

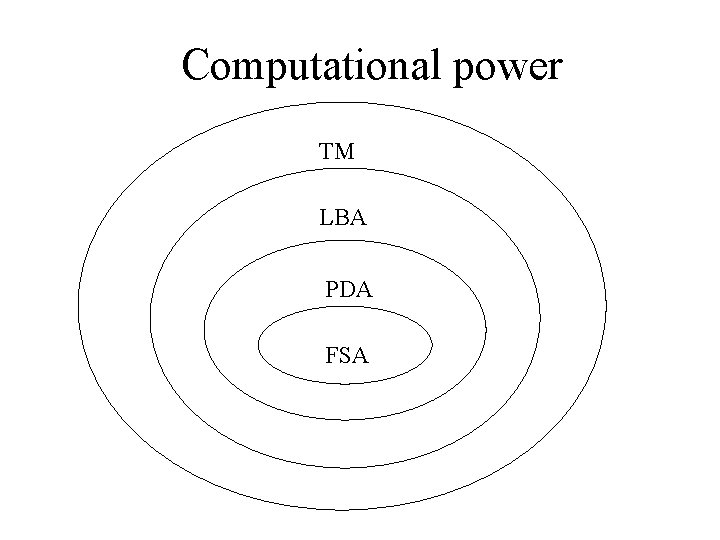
Computational power TM LBA PDA FSA

Review of set theory Can specify a set in two ways: - list of elements: A = {6, 12, 28} - characteristic property: B = {x | x is a positive, even integer} Set membership: 12 A, 9 A Set inclusion: A B (A is a subset of B) A B (A is a proper subset of B) Set operations: union: A {9, 12} = {6, 9, 12, 28} intersection: A {9, 12} = {12} difference: A - {9, 12} = {6, 28}

Set theory (continued) Another set operation, called “taking the complement of a set”, assumes a universal set. Let U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} be the universal set. Let A = {2, 4, 6, 8} Then = U - A = {0, 1, 3, 5, 7, 9} The empty set: = {}

Set theory (continued) The cardinality of a set, represented by |S|, is the number of elements in a set. Let S = {2, 4, 6} Then |S| = 3 The powerset of S, represented by 2 S, is the set of all subsets of S. 2 S = {{}, {2}, {4}, {6}, {2, 4}, {2, 6}, {4, 6}, {2, 4, 6}} The number of elements in a powerset is |2 S| = 2|S|

Formal language Alphabet = finite set of symbols or characters examples: = {a, b}, binary, ASCII String = finite sequence of symbols from an alphabet examples: aab, bbaba, also computer programs A formal language is a set of strings over an alphabet. Examples of formal languages over the alphabet = {a, b}: L 1 = {aa, aba, aababa, aa} L 2 = {all strings containing just two a’s and any number of b’s} A formal language can be finite or infinite.

Formal languages (continued) We often use string variables; u = aab, v = bbaba Operations on strings: length: |u| = 3 reversal: u. R = baa concatenation: uv = aabbbaba The empty string, denoted , has some special properties: | |=0 w=w =w

Formal languages (continued) If w is a string, then wn stands for the string obtained by repeating w n times. w 0 = + = * - { } L 0 = { } L 1 = L

Operations on languages Set operations: L 1 L 2 = {x | x L 1 or x L 2} is union L 1 L 2 = {x | x L 1 and x L 2} is intersection L 1 - L 2 = {x | x L 1 and x L 2} is difference = * - L L 1 L 2 = (L 1 - L 2) (L 2 - L 1) is complement is “symmetric difference”

Operations on languages String operations: LR = {w. R | w L} is “reverse of language” L 1 L 2 = {xy | x L 1, y L 2} is “concatenation of languages” L* = {x = x 1…xk | k 0 and x 1, …, xk L} = L 0 L 1 L 2. . is “Kleene star” or “star closure” L+ = L 1 L 2. . is “positive closure”

Some review questions • What is { , 01, 001} { , 00, 10}? • What is the concatenation of {0, 11, 010} and { , 10, 010}? • What are the 5 shortest strings in the language {0 i 1 i | i 0}? • What is the powerset {a, b, ab}?

Review of proof techniques • Knowing how to construct a formal proof is an important tool for the study of computer theory. • Inductive proof techniques work by: – Showing that if a statement holds true for one value of n (usually in the domain of natural numbers), then it must also hold true for n+1 – Demonstrating that it does hold for a specific value k

Review of proof techniques • Note that proof by induction does not assume what it wants to prove; that is, it does not assume that the statement is true for all n. • What it does do is to prove that if the statement is true for some specific value of n then it must be true for n+1. • But the other part of the proof is to show that the statement is, in fact, true for some specific value, k. Often k is 0 or 1. So we know that it is also true for k+1, k+2, k+3, etc.

Review of proof techniques • Let Sn denote the sum of the first n positive integers. • Using inductive proof, we want to show that for any n 1, Sn = (n (n + 1)) / 2.

Review of proof techniques • What is the basis for this proof? • Every inductive proof has the same pattern: • (a) we establish that some statement S(k) is true for some particular value of k [the basis], and then • (2) we prove that, if S(n) is true for n [the inductive hypothesis], it must be true for n + 1.

Review of proof techniques • When we ask, “What is the basis for this proof? ” we are asking, “what do we already know, or could show by demonstration if asked to do so. ” • Since the proof involves positive integers and the condition is that n 1, we start with n = 1: S 1 = (1 (1 + 1)) / 2 = 2 / 2 = 1 • This is our basis.

Review of proof techniques • What is the inductive hypothesis for this proof? • We know that Sk is true for some k, namely, k = 1. Our inductive hypothesis is that Sk is true for any k < (n + 1); that is: Sn = (n (n + 1)) / 2 • Our job will be to prove that Sn+1 is also true. That is, we must prove that: Sn+1 = ((n + 1)) / 2 • (This is our goal; we got this by substituting n + 1 for n in our inductive hypothesis. )

Review of proof techniques Goal: Prove that Sn+1 = ((n + 1)) / 2 Proof: 1) Sn+1 = 2) = 3) = 4) = 5) = 6) = 7) = 8) = 1+2+3+…+n+n+1 Sn + (n + 1) n (n + 1) / 2 + (n + 1) (n 2 + n) / 2 + (2 n + 2)/2 (n 2 + 3 n + 2) / 2 (n + 1) (n + 2) / 2 ((n + 1)) / 2 definition substitution ind. hyp. + sub. distribution mult. by 2/2 addition factoring 2=1+1

Review of proof techniques You don’t need to do these specific steps in this particular order, and you don’t need to list the justification for each step, but you somehow need to start from something we already know, and derive the goal statement, using the inductive hypothesis somewhere in the proof.

Review of proof techniques • The other main proof technique is proof by contradiction. In a proof by contradiction, we assume the opposite of what we want to prove, then show that this causes a contradictionto occur. This proves that our initial assumption must have been false.

Review of proof techniques Suppose that we want to prove that 2 is irrational. Proof: 1. By definition, if a real number x is rational then there exist two integers m and n such that x = m/n. 2. Assume that 2 is rational. 3. Then there are integers m’ and n’ such that 2 = m’/n’. 4. We divide m’ and n’ by all factors common to both m’ and n’, giving us two integers, m and n, with no common factors, and 2 = m/n.

Review of proof techniques 5. Since m/n = 2, m = n 2 6. Squaring both sides of the equation gives us: m 2 = n 2 2 7. Therefore, m 2 must be even, and consequently m must be even. 8. Since m is an even integer, m = 2 k, where k is also an integer. 9. Substituting, we see that (2 k)2 = 2 n 2. 10. Simplifying and canceling 2 from both sides gives us 2 k 2 = n 2. 11. Therefore, n 2 is even, and so n is even.

Review of proof techniques 12. Since n is an even integer, n = 2 j, where j is also an integer. 13. So we have now shown that m and n are both even, that is, m = 2 k and n = 2 j. 14. But this is a contradiction, since line 4 of our proof showed that the two integers, m and n, had no common factors. 15. Thus, or initial assumption, that 2 is rational, must be false. 16. Hence, 2 is irrational: QED.

Back to Formal Languages An important example of a formal language: • alphabet: ASCII symbols • string: a particular C++ program • formal language: set of all legal C++ programs The study of formal languages deals with: • Languages • Grammars • Automata

Grammars Definition 1. 1: A grammar G is defined as a quadruple: G = (V, T, S, P) where V is a finite set of objects called variables T is a finite set of objects called terminal symbols S V is a special symbol called the Start symbol P is a finite set of productions or "production rules" Sets V and T are nonempty and disjoint

Grammars Production rules have the form: x y where x is an element of (V T)+ and y is in (V T)* Given a string of the form w = uxv and a production rule x y we can apply the rule, replacing x with y, giving z = uyv We can then say that w z Read as "w derives z", or "z is derived from w"

Grammars If u v, v w, w x, x y, and y z, then we say: * u z This says that u derives z in an unspecified number of steps. Along the way, we may generate strings which contain variables as well as terminals. These are called sentential forms.

Grammars What is the relationship between a language and a grammar? Definition 1. 2: Let G = (V, T, S, P) The set * L(G) = {w T* : S w} is the language generated by G.

Grammars Consider the grammar G = (V, T, S, P), where: V = {S} T = {a, b} S = S, P = S a. Sb S

Grammars What are some of the strings in this language? S a. Sb ab S a. Sb aa. Sbb aabb S a. Sb aa. Sbb aaa. Sbbb aaabbb It is easy to see that the language generated by this grammar is: L(G) = {anbn : n 0} (See proof on pp. 22 -23 in Linz)

Grammars Let's go the other way, from a description of a language to a grammar that generates it. Find a grammar that generates: L = {anbn+1 : n 0} So the strings of this language will be: b (0 a's and 1 b) abb (1 a and 2 b's) aabbb (2 a's and 3 b's). . .

Grammars In order to generate a string with no a's and 1 b, you might want to write rules for the grammar that say: S ab a But you can't do this; a is a terminal, and you can't change a terminal, only variables

Grammars So, instead of: S ab a we create another variable, A (we often use capital letters to stand for variables), to use in place of the terminal, a: S Ab A

Grammars Now you might think that we can use another S rule here to generate the other part of the string, the anbn part S a. Sb But you can't, because that will generate ab, aabb, etc, which are not strings in our language. Note, however, that if we use A in place of S, that will solve our problem: A a. Ab

Grammars So, here are our rules: S Ab A a. Ab A The S Ab rule creates a single b terminal on the right, preceded by other strings (including possibly the empty string) on the left. The A rule allows the single b string to be generated. The A a. Ab rule and the A rule allows ab, aabb, aaabbb, etc. to be generated on the left side of the string.

Language-recognition problem • There are many types of computational problems. We will focus on the simplest, called the “languagerecognition problem. ” • Given a string, determine whether it belongs to a language or not. (Practical application for compilers: Is this a valid C++ program? ) • We study simple models of computation called “automata, ” and measure their computational power in terms of the class of languages they can recognize.

Automata, languages, and grammars • In this course, we will study the relationship between automata, languages, and grammars. • Recall that a formal language is a set of strings over a finite alphabet. • Automata are used to recognize languages. • Grammars are used to generate languages. • All of these concepts fit together.

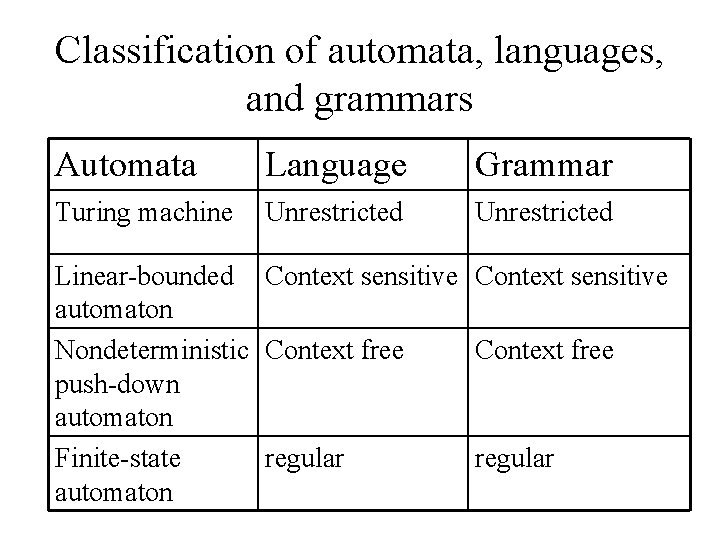
Classification of automata, languages, and grammars Automata Language Grammar Turing machine Unrestricted Linear-bounded Context sensitive automaton Nondeterministic Context free push-down automaton Finite-state regular automaton

Computability Theory Besides developing a theory of classes of languages and automata, we will study the limits of computation. We will consider the following two important questions: – What problems are impossible for a computer to solve? – What problems are too difficult for a computer to solve in practice (although possible to solve in principle)?

Uncomputable (undecidable) problems • Many well-defined (and apparently simple) problems cannot be solved by any computer • Examples: – For any program x, does x have an infinite loop? – For any two programs x and y, do these two programs have the same input/output behavior? – For any program x, does x meet its specification? (i. e. , does it have any bugs? )

Intractable problems • We will learn how to mathematically characterize the difficulty of computational problems. • There is a class of problems that can be solved in a reasonable amount of time and another class that cannot (What good is it for a problem to be solvable, if it cannot be solved in the lifetime of the universe? ) • The field of cryptography, for example, relies on the fact that the computational problem of “breaking a code” is intractable

Why study theory of computing? • This is the core mathematics of CS, and has not changed in over 30 years. • There are many applications, especially in design of compilers and programming languages. • It is important to be able to recognize uncomputable and intractable problems. • We need to know this in order to be a computer scientist, and not simply a computer programmer.