Ausgleichungsrechnung Einleitung Methode der kleinsten Quadrate Ausgleichungsverfahren Stochastisches

Ausgleichungsrechnung • • • Einleitung Methode der kleinsten Quadrate Ausgleichungsverfahren Stochastisches Modell a posteriori Anmerkungen Ausgleichungsrechnung I Gerhard Navratil

Aufgabe der Ausgleichsrechnung (Helmert 1872) Kontrolle durch überschüssige Messungen Vermehrung der Kontrollen führt zu größerer Annäherung an den wahren Wert, wenn nur zufällige Fehler auftreten Ziel: Resultat aus allen Beobachtungen bestimmen, das möglichst frei von zufälligen Fehlern ist Ausgleichungsrechnung I Gerhard Navratil

Bisher Messgrößen haben einen (unbekannten) wahren Wert Unsere Beobachtungen sind mit zufälligen Fehlern behaftet Aus Messgrößen werden oft andere Größen abgeleitet (z. B. Koordinaten aus Strecken und Richtungen) Für die abgeleiteten Größen kann eine Standardabweichung angegeben werden Ausgleichungsrechnung I Gerhard Navratil

Gewünscht Bisherige Erkenntnisse in einem größeren Kontext Ausdehnung auf komplexe Systeme Definition von Standard-Verfahren Ausgleichungsrechnung I Gerhard Navratil

Ziele • Kontrolle: Aufdecken von (groben) Fehlern • Plausibilität: Wahrscheinlichste Schätzwerte für die wahren Werte der Unbekannten bzw. Messwerte • Qualität: Angabe von Standardabweichungen für die Unbekannten und Messwerte Ausgleichungsrechnung I Gerhard Navratil

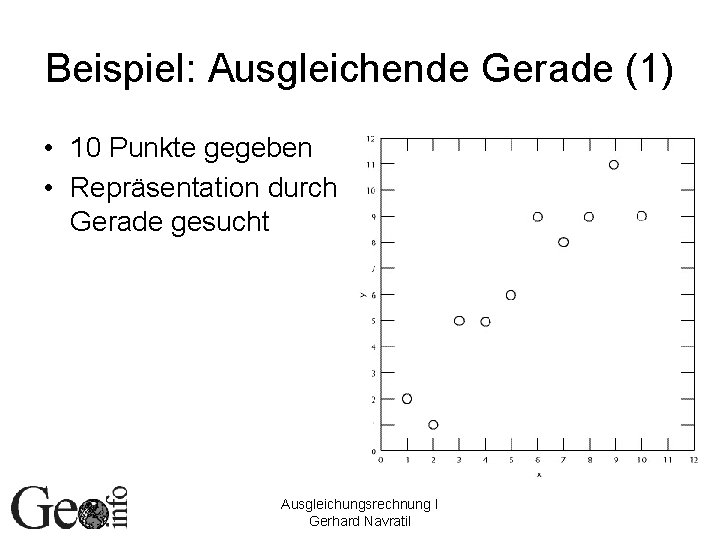
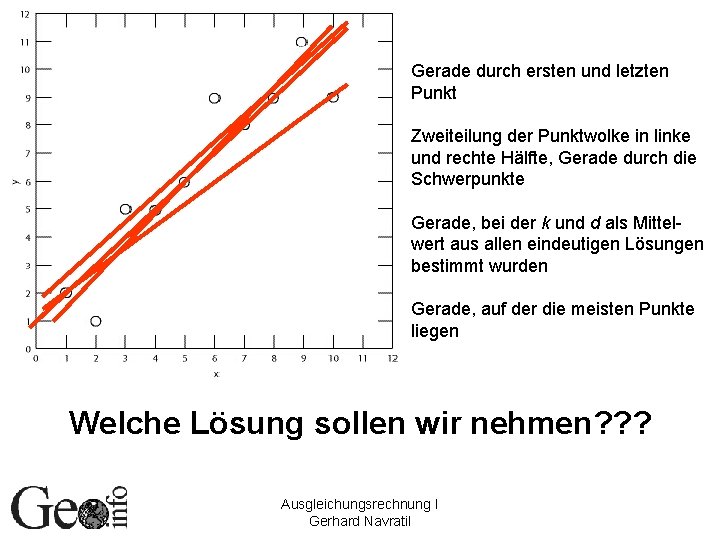
Beispiel: Ausgleichende Gerade (1) • 10 Punkte gegeben • Repräsentation durch Gerade gesucht Ausgleichungsrechnung I Gerhard Navratil

Beispiel: Ausgleichende Gerade (2) Mathematischer Ansatz: Jeder Punkt liefert eine Gleichung bzw. in Matrizenschreibweise Ausgleichungsrechnung I Gerhard Navratil

Beispiel: Ausgleichende Gerade (3) rk(A)=2, rk(A, L)=3 nicht lösbar Jeweils zwei Punkte liefern eine Lösung, die Lösungen passen nicht alle zusammen Gesucht: Möglichkeit, eine eindeutige Lösung zu ermitteln Ausgleichungsrechnung I Gerhard Navratil

Gerade durch ersten und letzten Punkt Zweiteilung der Punktwolke in linke und rechte Hälfte, Gerade durch die Schwerpunkte Gerade, bei der k und d als Mittelwert aus allen eindeutigen Lösungen bestimmt wurden Gerade, auf der die meisten Punkte liegen Welche Lösung sollen wir nehmen? ? ? Ausgleichungsrechnung I Gerhard Navratil

Beispiel: Ausgleichende Gerade (5) Annahme: Nur y-Werte sind Messwerte – x-Werte sind Konstante (varianzfrei) y-Werte bilden Beobachtungsvektor L Plausibelste Werte sind die, welchen nach der Statistik die höchste Wahrscheinlichkeit zukommt Annahme Normalverteilung für Messwerte Annahme mehr Beobachtungen als Unbekannte (Überbestimmung) Messwerte werden verbessert, sodass Ax=l gilt Ausgleichungsrechnung I Gerhard Navratil

Beispiel: Ausgleichende Gerade (6) Ax=l+v v=Ax-l Zusätzliche Bedingung: Ausgleichungsrechnung I Gerhard Navratil

Verteilung zufälliger Messabweichungen (1) • Lambert: Theorie der Zuverlässigkeit der Beobachtungen und Versuche (1765) – zufällige Abweichungen gleicher Größe nach beiden Seiten möglich – geringe Abweichungen häufiger als große – Kurve mit Wahrscheinlichkeit der Abweichungen ist • • symmetrisch Abweichung Null hat höchste Wahrscheinlichkeit Wendepunkt auf beiden Seiten beidseitig asymptotische Annäherung an Null • Gauß: Weitere Untersuchungen Normalverteilung Ausgleichungsrechnung I Gerhard Navratil

Verteilung zufälliger Messabweichungen (2) Folgerung: Messwerte sind normalverteilt zufällige Abweichungen normalverteilt Gilt auch, wenn Abweichungen aus empirischen Verbesserungen vi geschätzt Danach: Übergang von den einzelnen Abweichungen auf die Summe der Abweichungen Ausgleichungsrechnung I Gerhard Navratil

Verteilung zufälliger Messabweichungen (3) Gesamtwahrscheinlichkeitsdichte: Produkt der einzelnen Dichten Gesucht: Maximum, also jene vi, für die W maximal wird K minimal Ausgleichungsrechnung I Gerhard Navratil

Verteilung zufälliger Messabweichungen (4) Bedingung: oder in Matrizenschreibweise Gewichte pi umgekehrt proportional zu den Varianzen Ausgleichungsrechnung I Gerhard Navratil

Stochastisches Modell a priori Die Gewichtsmatrix Beschreibung der stochastischen Zusammenhänge in einem Zufallsvektor: Kovarianzmatrix Für einen Beobachtungsvektor: – Hauptdiagonale: Varianz der Beobachtung – Außerhalb der Hauptdiagonale: Kovarianz oder Null wenn stochastisch unabhängig Bezeichnet mit SLL Ausgleichungsrechnung I Gerhard Navratil

Festlegung von Gewichten (1) Gewichtung der Verbesserungen umgekehrt proportional zu den Varianzen Oft nur relative Genauigkeiten vorhanden Wir wählen Bezugsvarianz: Varianz der Gewichtseinheit a priori oder Varianzfaktor Kofaktormatrix Ausgleichungsrechnung I Gerhard Navratil

Festlegung von Gewichten (2) Elemente der Kofaktormatrix: Kofaktoren oder Gewichtsreziproke Gewichtung ist umgekehrt proportional zu den Varianzen bzw. Kofaktoren, also Inversion der Matrix Festlegung geschieht vor der Messung bzw. Ausgleichung a priori Varianzen Varianz der Gewichtseinheit a priori stochastisches Modell a priori Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell (1) n Beobachtungen L um u Unbekannte X (Parametervektor) zu bestimmen Realisierungen L 1, … Ln sind Näherungen des wahren Wertes Wir geben Schätzwert für den wahren Wert an: Ausgeglichene Beobachtungen Auch Parametervektor hat wahren Wert Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell (2) Oft Parameter näherungsweise bekannt: Genäherter Parametervektor X 0 Differenz ausgeglichener – genäherter Parametervektor: gekürzter Parametervektor x Funktionaler Zusammenhang: r Funktionen j 1, … jr mit den Parametern L und X Ausgleichungsrechnung I Gerhard Navratil

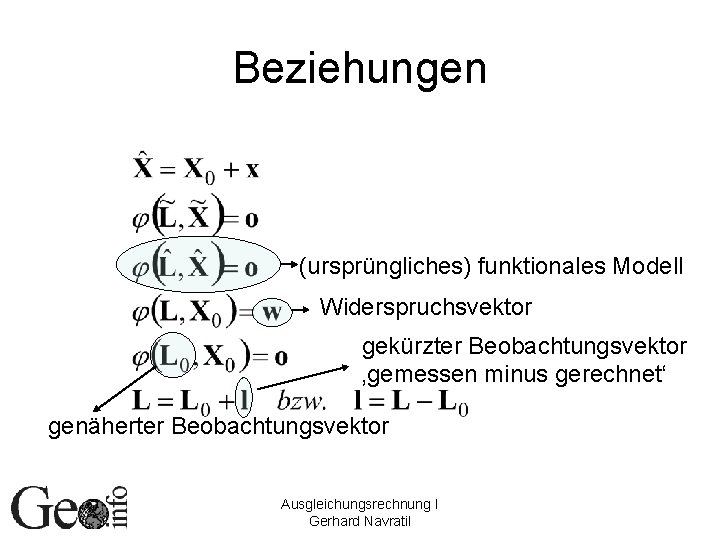
Beziehungen (ursprüngliches) funktionales Modell Widerspruchsvektor gekürzter Beobachtungsvektor ‚gemessen minus gerechnet‘ genäherter Beobachtungsvektor Ausgleichungsrechnung I Gerhard Navratil

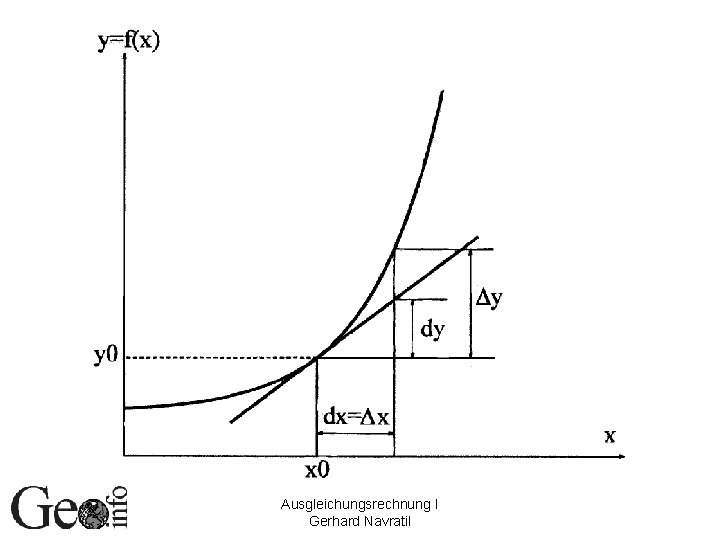
Linearisiertes funktionales Modell Funktionen j 1, … jr von beliebigem Typ Annahme: x und v klein gegenüber X 0 und L Linearisierung über Taylor-Entwicklung Ausgleichungsrechnung I Gerhard Navratil

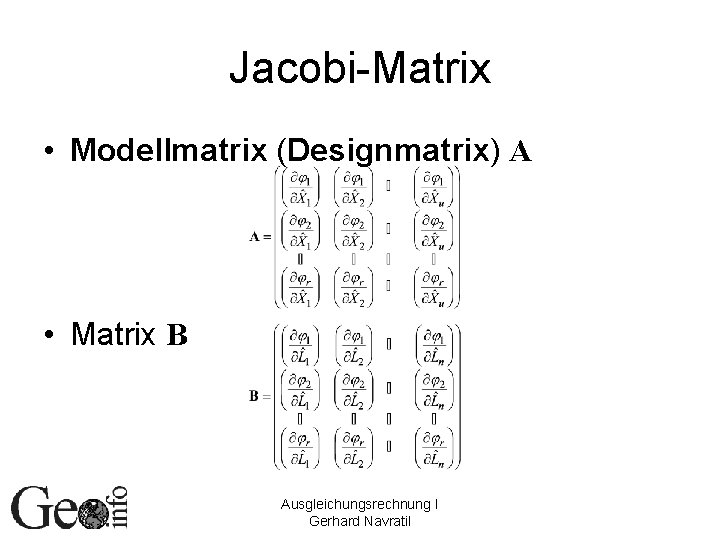
Jacobi-Matrix • Modellmatrix (Designmatrix) A • Matrix B Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell Ausgleichungsrechnung I Gerhard Navratil

Allgemeine Auflösung (1) Extremwertaufgabe mit Nebenbedingungen Lösung mit Lagrange‘schen Vektoren Partielle Ableitungen bilden und gleich Null setzen Ausgleichungsrechnung I Gerhard Navratil

Allgemeine Auflösung (2) Ableitung nach v: Gleich Null setzen: Ausgleichungsrechnung I Gerhard Navratil

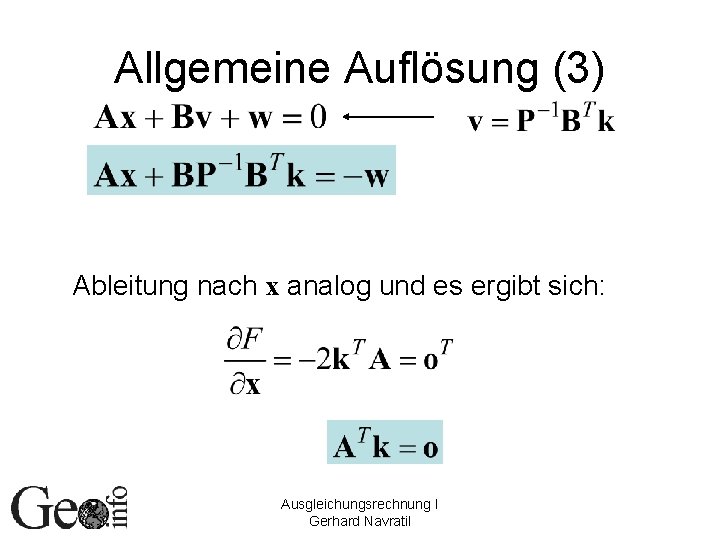
Allgemeine Auflösung (3) Ableitung nach x analog und es ergibt sich: Ausgleichungsrechnung I Gerhard Navratil

Allgemeine Auflösung (4) Gemeinsames Gleichungssystem: Auflösung durch Inversion: Allgemeinfall der Ausgleichungsrechnung Ausgleichung bedingter Beobachtungen mit Verbesserungsgleichungen Ausgleichungsrechnung I Gerhard Navratil

Hauptprobe Annahme war, dass x und v klein gegenüber X 0 und L sind Annahme muss überprüft werden! Einsetzen in ursprüngliches (nicht linearisiertes) Gleichungssystem Wenn nicht genügend genau erfüllt? Iteration – Näherungswerte nicht gut genug Neu aufstellen – Funktionales Modell fehlerhaft Geprüfte Programme verwenden – Rechenfehler Ausgleichungsrechnung I Gerhard Navratil

Ausgleichungsrechnung I Gerhard Navratil

Fehler im funktionalen Modell Hauptprobe zeigt Fehler im funktionalen Modell an Kandidat für Fehler ist die Funktion, bei der die Hauptprobe nicht aufgeht z. B. 3. Gleichung geht nicht auf – möglicherweise 3. Zeile der A-Matrix oder 3. Element des w-Vektors fehlerhaft Ausgleichungsrechnung I Gerhard Navratil

Iterative Ausgleichung Ergebnis der Ausgleichung als Näherung für eine neuerliche Ausgleichung verwendet L, SLL und B bleiben erhalten A und w werden neu berechnet (hier kommen die Näherungswerte der Unbekannten vor) Iteration so lange, bis Hauptprobe aufgeht Iteration muss nicht konvergieren! Ausgleichungsrechnung I Gerhard Navratil

Sonderfälle 1. In jeder Gleichung ji kommt jeweils nur eine Beobachtung vor: Ausgleichung vermittelnder Beobachtungen 2. Es treten keine unbekannten Parameter auf, die Gleichungen ji beschreiben nur den funktionalen Zusammenhang der Beobachtungen: Ausgleichung bedingter Beobachtungen 3. In n Gleichungen tritt jeweils nur eine Beobachtung auf und in den übrigen r-n Gleichungen treten nur Unbekannte auf: Ausgleichung vermittelnder Beobachtungen mit Bedingungsgleichungen Ausgleichungsrechnung I Gerhard Navratil

Ausgleichung vermittelnder Beobachtungen Pro Gleichung nur eine Beobachtung Gleichungen explizit nach Li auflösbar n Messgrößen, r=n Gleichungen, u Unbekannte Überschüssige Beobachtungen: nfu=n-u Anzahl der Freiheitsgrade (Redundanz) Ausgleichungsrechnung I Gerhard Navratil

Art des Problems Unterscheidung über die Redundanz: • Redundanz < 0: unterbestimmt, nicht eindeutig lösbar • Redundanz = 0: Problem eindeutig lösbar • Redundanz > 0: Ausgleichungsaufgabe Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell Taylorentwicklung: B= –I Modellmatrix A wie bisher weiters: bzw. Verbesserungsgleichung Ausgleichungsrechnung I Gerhard Navratil

Gewichtsmatrix Anwendung des Varianzfortpflanzungsgesetzes auf gibt für die Kovarianzmatrix des gekürzten Beobachtungsvektors: Die Kofaktormatrix ergibt sich somit zu Somit erhalten wir dieselbe Gewichtsmatrix P wie bisher. Ausgleichungsrechnung I Gerhard Navratil

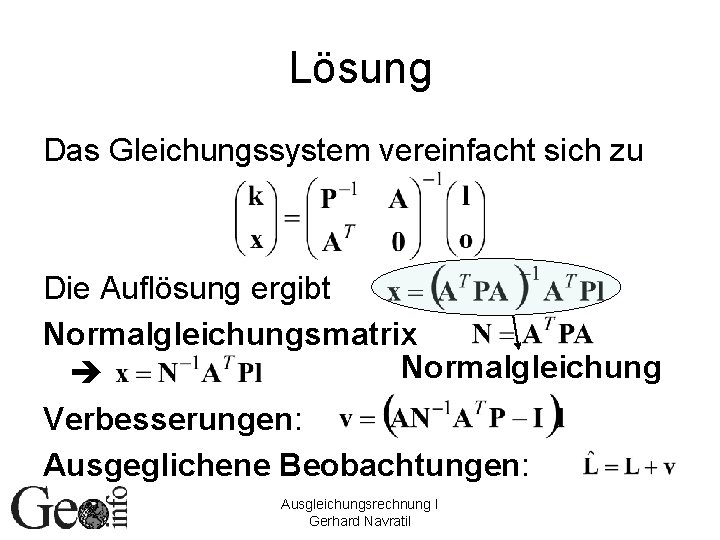
Lösung Das Gleichungssystem vereinfacht sich zu Die Auflösung ergibt Normalgleichungsmatrix Normalgleichung Verbesserungen: Ausgeglichene Beobachtungen: Ausgleichungsrechnung I Gerhard Navratil

Hauptprobe Erfüllen die ausgeglichenen Beobachtungen und ausgeglichenen Parameter das ursprüngliche funktionale Modell? Einsetzen in Ausgleichungsrechnung I Gerhard Navratil

Sonderfall: Lineare Verbesserungsgleichungen z. B. Koordinatendifferenzen (Nivellement) Verbesserungsgleichungen sind linear Keine Linearisierung notwendig Keine Näherungswerte für die Parameter notwendig (oft trotzdem aus numerischen Gründen verwendet – kleine Werte in x und l) Hauptprobe: Nur aufgestelltes Modell und Rechnung können falsch sein Ausgleichungsrechnung I Gerhard Navratil

Sonderfall: Ausgleichung direkter Beobachtungen z. B. Ausgleichung direkt und mehrfach gemessener Größen (Strecke) A-Matrix ist ein 1 -Vektor Auflösung: Gewichtsmatrix Einheitsmatrix: einfaches arithmetisches Mittel Gewichtsmatrix Diagonalmatrix: gewogenes arithmetisches Mittel Sonst: allgemeines arithmetisches Mittel Ausgleichungsrechnung I Gerhard Navratil

Ausgleichung bedingter Beobachtungen Keine unbekannten Parameter n Beobachtungen sollen so verbessert werden, dass sie r Bedingungen (sind aufzustellen) erfüllen r = n – n 0 mit n 0 = Anzahl der notwendigen Beobachtungen für eine eindeutige Lösung nfb=r Anzahl der Freiheitsgrade (Redundanz) Das Problem vereinfacht sich zu Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell Widerspruchsvektor: Ableitungen nach X alle Null, somit A-Matrix eine Nullmatrix, also Korrelaten: Verbesserungen: Normalgleichungsmatrix der bedingten Ausgleichung: Ausgleichungsrechnung I Gerhard Navratil

Hauptprobe Erfüllen die ausgeglichenen Beobachtungen das ursprüngliche funktionale Modell? Einsetzen in Ausgleichungsrechnung I Gerhard Navratil

Ausgleichung vermittelnder Beobachtungen mit Bedingungsgleichungen Pro Gleichung nur eine Beobachtung Zusätzlich Bedingungen zwischen den Unbekannten n Beobachtungen, u Unbekannte, nb Bedingungen nfvb = n – u + nb = r – u Anzahl der Freiheitsgrade (Redundanz) Ausgleichungsrechnung I Gerhard Navratil

Lösungsansätze • Elimination von Unbekannten: r Unbekannte werden mit Hilfe der Bedingungen eliminiert • Strenge Lösung: Extremwertaufgabe mit Nebenbedingungen • Fiktive Beobachtungen: Bedingungen werden als (fiktive) Beobachtungen mit großem Gewicht eingeführt Ausgleichungsrechnung I Gerhard Navratil

Wann Ausgleichungsproblem? nfvb = n – u + r Ausgleichungsproblem, wenn nfvb > 0 Somit: n + r > u Die Summe aus Beobachtungen und Bedingungen muss größer als die Anzahl der Unbekannten sein Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell der vermittelnden Ausgleichung und die Bedingungen Getrennte Betrachtung der beiden Teile: Beobachtungen Bedingungen Keine Bedingungen zwischen den Beobachtungen B ist eine Nullmatrix Ausgleichungsrechnung I Gerhard Navratil

Lösung (1) Methode von Langrange: Differenziert und gleich Null gesetzt: Einsetzen von gibt Ausgleichungsrechnung I Gerhard Navratil

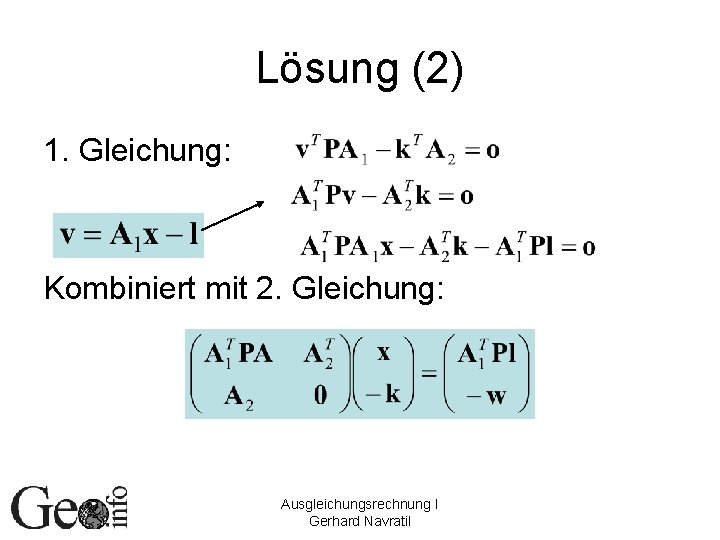
Lösung (2) 1. Gleichung: Kombiniert mit 2. Gleichung: Ausgleichungsrechnung I Gerhard Navratil

Hauptprobe Erfüllen die ausgeglichenen Beobachtungen und ausgeglichenen Parameter das ursprüngliche funktionale Modell? Erfüllen die ausgeglichenen Parameter die Bedingungen? Einsetzen in Ausgleichungsrechnung I Gerhard Navratil

Ausgleichung bedingter Beobachtungen mit Verbesserungsgleichungen Entspricht dem Allgemeinfall der Ausgleichungsrechnung n Beobachtungen, n 0 Beobachtungen zur eindeutigen Lösung notwendig, u Unbekannte Anzahl der aufzustellenden Bedingungen: r = (n – n 0) + u = nfa + u Lösung: siehe Allgemeinfall Ausgleichungsrechnung I Gerhard Navratil

Stochastisches Modell a posteriori: nach der Ausgleichung Beim stochastischen Modell a priori Ausgangspunkt Kovarianzmatrix, aber schließlich verwendet die Kofaktormatrix Kovarianzfortpflanzungsgesetz angewendet auf Gleichungssystem f=Fx gibt Kofaktorfortpflanzungsgesetz Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der vermittelnden Ausgleichung (1) gekürzter Beobachtungsvektor: Ausgeglichene Beobachtungen aus Somit gilt: Nun können wir l, x, von l ausdrücken. und v als Funktion Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der vermittelnden Ausgleichung (2) Das Kofaktorfortpflanzungsgesetz liefert: Gesuchte Kofaktoren in der Hauptdiagonale Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der vermittelnden Ausgleichung (3) Und weiters: Grund: Unterscheiden sich nur durch konstante Faktoren Ausgleichungsrechnung I Gerhard Navratil

Probe Gewichtsreziprokenprobe nach Ansermet Die Summe der Hauptdiagonalglieder Produktmatrix muss gleich der Anzahl der Unbekannten sein Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der bedingten Ausgleichung (1) Ausgangspunkt: (ausgehend von mit anschließender Taylor. Entwicklung für w: Wenn die Näherungswerte genau genug, kann der Restfehler o 2 vernachlässigt werden Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der bedingten Ausgleichung (2) Somit wird zu Und es gilt Nun können wir alle Werte als Funktion von L darstellen Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der bedingten Ausgleichung (3) Das Kovarianzfortpflanzungsgesetz liefert: Gesuchte Kofaktoren in der Hauptdiagonale Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der vermittelnde Ausgleichung mit Bed. Interessante Kofaktormatrizen direkt aus der invertierten Normalgleichungsmatrix: Und weiters: Ausgleichungsrechnung I Gerhard Navratil

Kofaktoren a posteriori bei der bed. Ausgleichung mit Unbekannten Interessante Kofaktormatrizen direkt aus der invertierten Normalgleichungsmatrix: Und weiters: Ausgleichungsrechnung I Gerhard Navratil

Varianz der Gewichtseinheit a posteriori (1) Im stochastischen Modell s 02 herausgehoben und die Kofaktormatrix Q erhalten Somit Übergang auf relative Genauigkeitsangaben (ausreichend für Gewichtung) Ausgleichung liefert Kofaktormatrizen für ausgeglichene Parameter etc. Gesucht: Kovarianzmatrizen Multiplikation mit Varianz der Gewichtseinheit a posteriori Ausgleichungsrechnung I Gerhard Navratil

Varianz der Gewichtseinheit a posteriori (2) Parameter aus den empirischen Beobachtungen bestimmt auch Varianz der Gewichtseinheit a posteriori empirisch bestimmt Definition der Varianz: Quadratsumme der Verbesserungen durch Anzahl der Freiheitsgrade Ausgleichungsrechnung I Gerhard Navratil

Varianzen, Kovarianzen und Standardabweichungen Aus Kofaktormatrizen durch Multiplikation mit der Varianz der Gewichtseinheit a posteriori z. B. Varianz einer Funktion Ausgleichungsrechnung I Gerhard Navratil

Funktionales Modell Ausgleichung vermittelnder Beobachtungen: Designmatrix enthält Ableitungen nach den Unbekannten Formeln für Elemente der Designmatrix für Standardbeobachtungen einfach herzuleiten – Streckenbeobachtung – Richtungsbeobachtung Formeln für andere Beobachtungen analog Ausgleichungsrechnung I Gerhard Navratil

Streckenbeobachtung Ableitungen: Werte der A-Matrix Ausgleichungsrechnung I Gerhard Navratil

Richtungsbeobachtung Ableitungen: Werte der A-Matrix Ausgleichungsrechnung I Gerhard Navratil

Bedingungsgleichungen Probleme bei der bedingten Ausgleichung – Anzahl der Bedingungen festlegen (Redundanz) – Linear unabhängige Bedingungen aufstellen Wann? Anzahl der Unbekannten größer als Redundanz (Matrixgröße) Ausgleichungsrechnung I Gerhard Navratil

Höhennetze Mögliche Bedingungen sind: • Höhendifferenz geschlossener Schleifen ist gleich Null • Höhendifferenz zwischen zwei bekannten Punkten ist gleich der Summe der Höhen der Teilstücke Ausgleichungsrechnung I Gerhard Navratil

Winkelmessung Mögliche Bedingungen sind: • Winkelsumme im ebenen Dreieck ist 200 g a+b+g– 200=0 • Winkelsumme im Vieleck • Winkelsumme einer abgeschlossenen Satzmessung ist 400 g a+b+g– 400=0 • Winkelsumme einer nicht abgeschlossenen Satzmessung ist Ausgleichungsrechnung I Gerhard Navratil

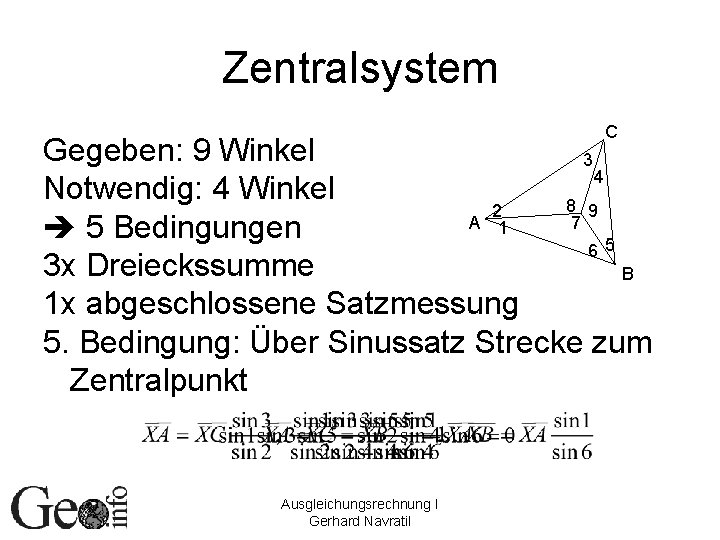
Zentralsystem C Gegeben: 9 Winkel 3 4 Notwendig: 4 Winkel 8 9 2 A 1 7 5 Bedingungen 65 3 x Dreieckssumme B 1 x abgeschlossene Satzmessung 5. Bedingung: Über Sinussatz Strecke zum Zentralpunkt Ausgleichungsrechnung I Gerhard Navratil

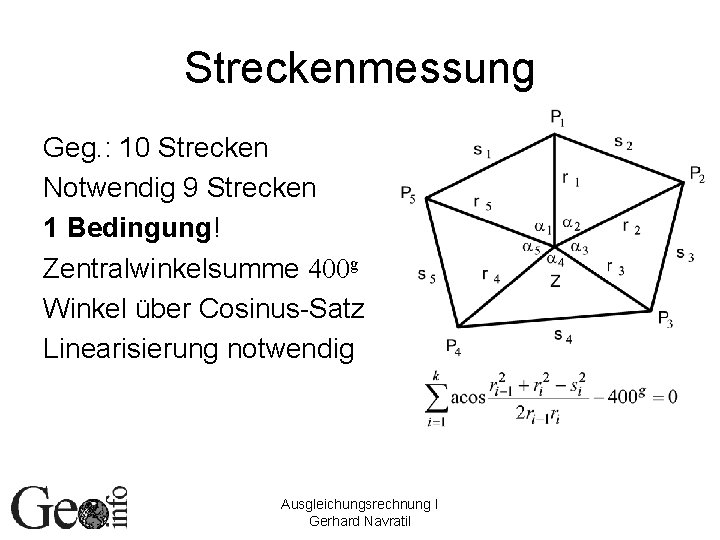
Streckenmessung Geg. : 10 Strecken Notwendig 9 Strecken 1 Bedingung! Zentralwinkelsumme 400 g Winkel über Cosinus-Satz Linearisierung notwendig Ausgleichungsrechnung I Gerhard Navratil

Große Netze Bei großen Netzen auch große Matrizen Inversion großer Matrizen ist auch heute noch ein Problem (Rechenzeit von Tagen) Daher Strategien zur Reduktion der Größe Netze der Landesvermessung: Bedingte Ausgleichung Elimination von Parametern durch Blockzerlegung Ausgleichungsrechnung I Gerhard Navratil

Elimination von Parametern durch Blockzerlegung (1) Allgemeingültiger Ansatz Blockweise Reduktion des funktionalen Modells Zerlegung in Submatrizen und -Vektoren: Verbesserungsgleichungen: Ausgleichungsrechnung I Gerhard Navratil

Elimination von Parametern durch Blockzerlegung Zuschläge auf die Unbekannten: 2. Gleichung: Falls existiert erhalten wir eine Bestimmungsgleichung für x 2 Einsetzen in x 1 Lösung für x 1 Ausgleichungsrechnung I Gerhard Navratil

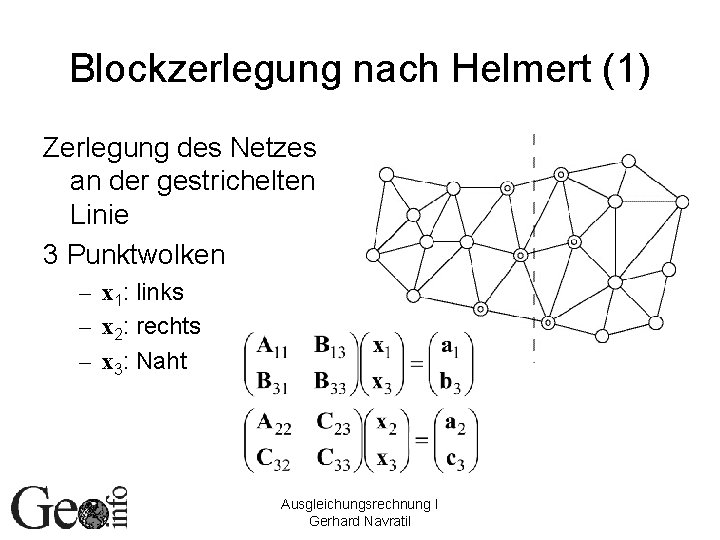
Blockzerlegung nach Helmert (1) Zerlegung des Netzes an der gestrichelten Linie 3 Punktwolken – x 1: links – x 2: rechts – x 3: Naht Ausgleichungsrechnung I Gerhard Navratil

Blockzerlegung nach Helmert (2) Nun werden die Parameter x 1 und x 2 aus den Gleichungssystemen eliminiert: Die partiell reduzierten Anteile werden addiert: Lösung von x 1 und x 2 bestimmen Ausgleichungsrechnung I Gerhard Navratil

Weitere Bezeichnungen • Parameterschätzung nach der L 2 -Norm • Vermittelnde Ausgleichung: Gauß-Markov-Modell • Allgemeinfall der Ausgleichungsrechnung: Gauß-Helmert-Modell • Ausgleichungsen vermittelnder Beobachtungen mit Bedingungsgleichungen: Ausgleichung nach Parametern mit Restriktionen Ausgleichungsrechnung I Gerhard Navratil

Analogien • Statik: Durchbiegung bei Fachwerk- und Stabsystemen – Arbeit minimiert • Elektrizitätslehre: Leitungsnetze – Stromwärme minimiert • Kinetische Gastheorie: bei irreversiblen Prozessen wird die Entropie maximiert • Dynamik: Bewegung eines Massenpunktes – Summe der durch Zwangsbedingungen verlorenen Kräfte minimiert Ausgleichungsrechnung I Gerhard Navratil

Zusammenfassung • Lösung überbestimmter Probleme durch Einführen einer Bedingung: v. Tv min • Extremwertaufgabe mit Nebenbedingung • Sonderfälle bedingte/vermittelnde Ausgleichung – vermitteln: einfach zu automatisieren – bedingt: schwer aufzustellen, einfach zu rechnen • Große Netze: Zerlegung oder bedingte A. Ausgleichungsrechnung I Gerhard Navratil