Shape Analysis via 3 Valued Logic Mooly Sagiv

Shape Analysis via 3 -Valued Logic Mooly Sagiv Tel Aviv University http: //www. cs. tau. ac. il/~msagiv/toplas 02. ps www. cs. tau. ac. il/~tvla

Topics • A new abstract domain for static analysis • Abstract dynamically allocated memory • TVLA: A system for generating abstract interpreters • Applications

Motivation • Dynamically allocated storage and pointers are essential programming tools – Object oriented – Modularity – Data structure • But – Error prone – Inefficient • Static analysis can be very useful here

A Pathological C Program a = malloc(…) ; b = a; free (a); c = malloc (…); if (b == c) printf(“unexpected equality”);

Dereference of NULL pointers typedef struct element { bool search(int value, Elements *c) { int value; Elements *elem; struct element *next; for (elem = c; } Elements c != NULL; elem = elem->next; ) if (elem->val == value) return TRUE; return FALSE

Dereference of NULL pointers typedef struct element { bool search(int value, Elements *c) { int value; Elements *elem; struct element *next; for (elem = c; } Elements c != NULL; potential null de-reference elem = elem->next; ) if (elem->val == value) return TRUE; return FALSE

Memory leakage typedef struct element { int value; struct element *next; } Elements* reverse(Elements *c) { Elements *h, *g; h = NULL; while (c!= NULL) { g = c->next; h = c; c->next = h; c = g; } return h;

Memory leakage typedef struct element { int value; struct element *next; } Elements leakage of address pointed-by h Elements* reverse(Elements *c) { Elements *h, *g; h = NULL; while (c!= NULL) { g = c->next; h = c; c->next = h; c = g; } return h;

Memory leakage typedef struct element { int value; struct element *next; } Elements ✔ No memory leaks Elements* reverse(Elements *c) { Elements *h, *g; h = NULL; while (c!= NULL) { g = c->next; h = c; c->next = h; c = g; } return h;

Example: List Creation typedef struct node { int val; struct node *next; } *List; List create (…) { List x, t; x = NULL; while (…) do { t = malloc(); t next=x; x = t ; } return x; } ✔ No null dereferences ✔ No memory leaks ✔ Returns acyclic list

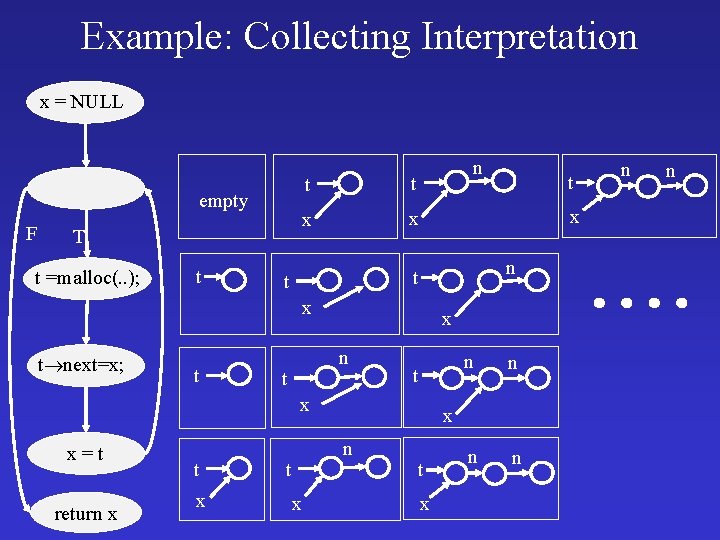
Example: Collecting Interpretation x = NULL empty F T t =malloc(. . ); t n t t x x x n t t x t next=x; t x n t t x x=t return x t x x n n x n t t t x n n

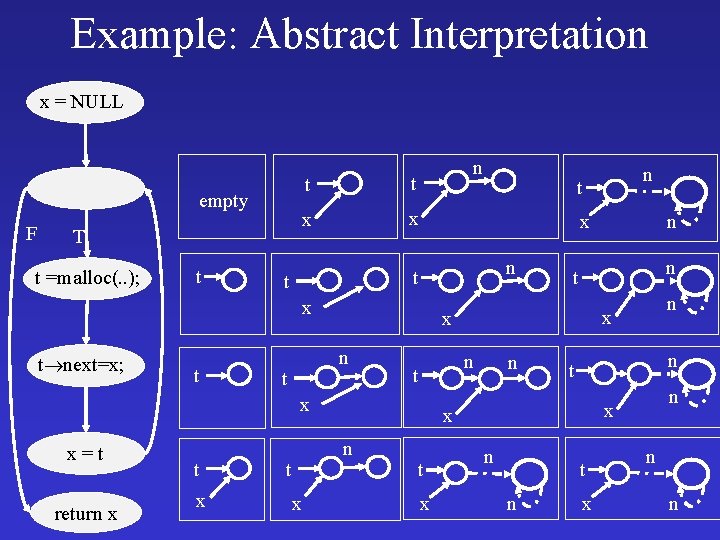
Example: Abstract Interpretation x = NULL empty F T t =malloc(. . ); t n t t x x n x t next=x; t t t return x t x n n t t x n x x n n x x=t n t x n n x t t n t n x n n

Challenge 1 - Memory Allocation • The number of allocated objects/threads is not known • Concrete state space is infinite • How to guarantee termination?

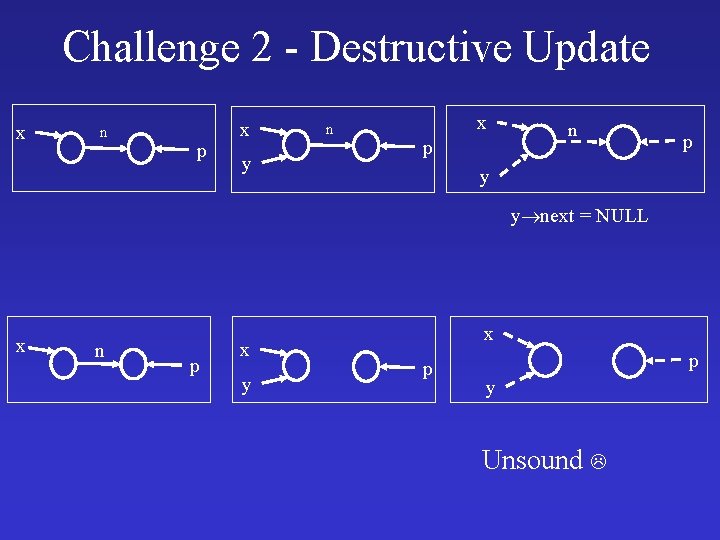
Challenge 2 - Destructive Updates • The program manipulates states using destructive updates – e next = t • Hard to define concrete interpretation • Harder to define abstract interpretation

Challenge 2 - Destructive Update x n p x y n x p n p y y next = NULL x n p x y x p p y Unsound

Challenge 2 - Destructive Update x n p y y next = NULL x n y Imprecise p

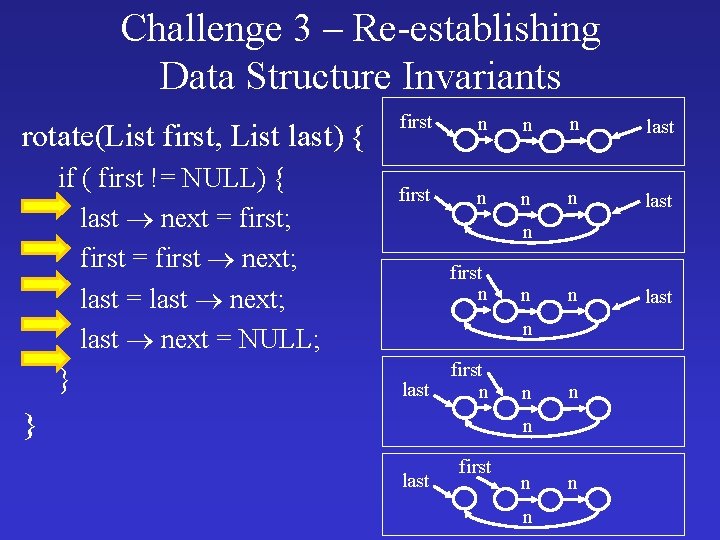
Challenge 3 – Re-establishing Data Structure Invariants • Data-structure invariants typically only hold at the beginning and end of ADT operations • Need to verify that data-structure invariants are re-established

Challenge 3 – Re-establishing Data Structure Invariants rotate(List first, List last) { if ( first != NULL) { last next = first; first = first next; last = last next; last next = NULL; } first n n n last n first n n n last first n } n n n last first n n n

Plan • Concrete interpretation • Canonical abstraction • Abstract interpretation using canonical abstraction • The TVLA system

Traditional Heap Interpretation • States = Two level stores – Env: Var Values – fields: Loc Values – Values=Loc Atoms • Example – Env = [x 30, p 79] – next = [30 40, 40 50, 50 79, 79 90] – val = [30 1, 40 2, 50 3, 79 4, 90 5] x 30 1 40 40 2 50 3 p 90 79 50 79 4 90 5 0

Predicate Logic • Vocabulary – A finite set of predicate symbols P each with a fixed arity • Logical Structures S provide meaning for predicates – A set of individuals (nodes) U – p. S: (US)k {0, 1} • FOTC over TC, express logical structure properties

Representing Stores as Logical Structures • • Locations Individuals Program variables Unary predicates Fields Binary predicates Example – U = {u 1, u 2, u 3, u 4, u 5} – x = {u 1}, p = {u 3} – n = {<u 1, u 2>, <u 2, u 3>, <u 3, u 4>, <u 4, u 5>} x u 1 n u 2 p n u 3 n u 4 n u 5

Formal Semantics of First Order Formulae • • For a structure S=<US, p. S> Formulae with LVar free variables Assignment z: LVar US S(z): {0, 1} 1 S(z)=1 0 S(z)=0 p (v 1, v 2, …, vk) S(z)=p. S (z(v 1), z(v 2), …, z(vk))

Formal Semantics of First Order Formulae • • For a structure S=<US, p. S> Formulae with LVar free variables Assignment z: LVar US S(z): {0, 1} 1 2 S(z)=max ( 1 S(z), 2 S(z)) 1 2 S(z)=min ( 1 S(z), 2 S(z)) 1 S(z)=1 - 1 S(z) v: 1 S(z)=max { 1 S(z[v u]) : u US}

Formal Semantics of Transitive Closure • • For a structure S=<US, p. S> Formulae with LVar free variables Assignment z: LVar US S(z): {0, 1} p*(v 1, v 2) S(z) = max {u 1, . . . , uk U, Z(v 1)=u 1, Z(v 2)=uk} min{1 i < k} p. S(ui, ui+1)

Concrete Interpretation Rules Statement Update formula x =NULL x’(v)= 0 x= malloc() x’(v) = Is. New(v) x=y x’(v)= y(v) x=y next x’(v)= w: y(w) n(w, v) x next=y n’(v, w) = ( x(v) n(v, w)) (x(v) y(w))

Invariants • No memory leaks v: {x PVar} w: x(w) n*(w, v) • Acyclic list(x) v, w: x(v) n*(v, w) n+(w, v) • Reverse (x) v, w, r: x(v) n*(v, w) n(w, r) n’(r, w)

Why use logical structures? • Naturally model pointers and dynamic allocation • No a priori bound on number of locations • Use formulas to express semantics • Indirect store updates using quantifiers • Can model other features – Concurrency – Abstract fields

Why use logical structures? • Behaves well under abstraction • Enables automatic construction of abstract interpreters from concrete interpretation rules (TVLA)

Collecting Interpretation • The set of reachable logical structures in every program point • Statements operate on sets of logical structures • Cannot be directly computed for programs with unbounded store and loops x = NULL; while (…) do { t = malloc(); empty x u 1 t } x t n u 2 t t next=x; x=t u 1 x u 1 n u 2 n … n un

Plan • Concrete interpretation • Canonical abstraction • TVLA

Canonical Abstraction • Convert logical structures of unbounded size into bounded size • Guarantees that number of logical structures in every program is finite • Every first-order formula can be conservatively interpreted

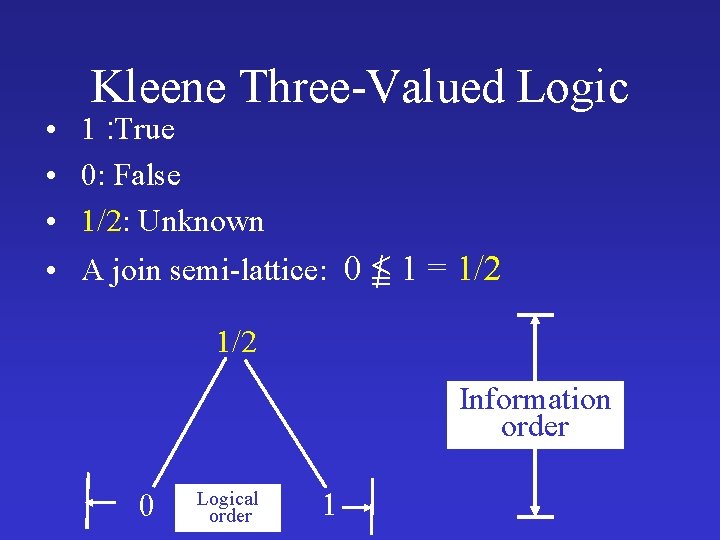
Kleene Three-Valued Logic • 1 : True • 0: False • 1/2: Unknown • A join semi-lattice: 0 1 = 1/2 Information order Logical order

Boolean Connectives [Kleene]

3 -Valued Logical Structures • A set of individuals (nodes) U • Predicate meaning – p. S: (US)k {0, 1, 1/2}

Canonical Abstraction • Partition the individuals into equivalence classes based on the values of their unary predicates – Every individual is mapped into its equivalence class • Collapse predicates via – p. S (u’ 1, . . . , u’k) = {p. B (u 1, . . . , uk) | f(u 1)=u’ 1, . . . , f(u’k)=u’k) } • At most 2 A abstract individuals

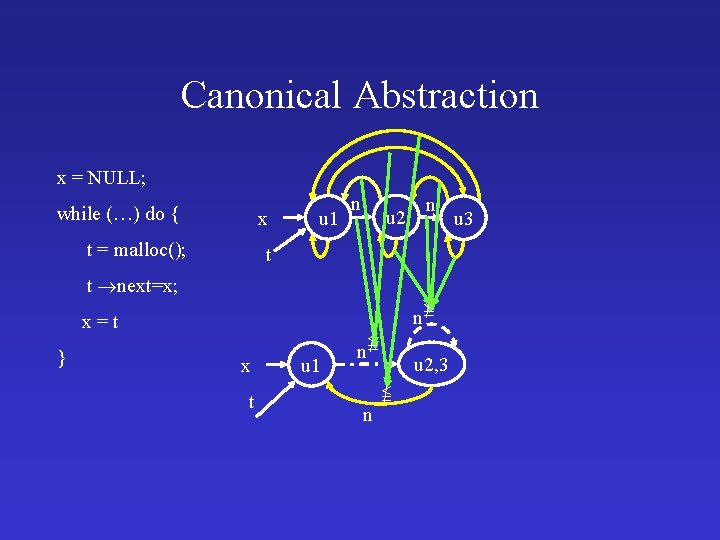
Canonical Abstraction x = NULL; while (…) do { x t = malloc(); u 1 n u 2 n t t next=x; x=t } x t u 1 n u 2, 3 n u 3

Canonical Abstraction x = NULL; while (…) do { x t = malloc(); u 1 n n u 2 t t next=x; n x=t } x t u 1 n u 2, 3 n u 3

Canonical Abstraction and Equality • Summary nodes may represent more than one element • (In)equality need not be preserved under abstraction • Explicitly record equality • Summary nodes are nodes with eq(u, u)=1/2

Canonical Abstraction and Equality eq x = NULL; while (…) do { eq x t = malloc(); u 1 n u 2 t t next=x; eq eq x=t } eq eq x t u 1 eq n n u 3 eq eq u 2, 3 n eq

Canonical Abstraction x = NULL; while (…) do { x t = malloc(); u 1 n u 2 n t t next=x; x=t } x t u 1 n u 2, 3 n u 3

Challenges: Heap & Concurrency [Yahav POPL’ 01] • Concurrency with the heap is evil… • Java threads are just heap allocated objects • Data and control are strongly related – Thread-scheduling info may require understanding of heap structure (e. g. , scheduling queue) – Heap analysis requires information about thread scheduling Thread t 1 = new Thread(); Thread t 2 = new Thread(); … t = t 1; … t. start();

Configurations – Example held_by at[l_1] rval[my. Lock] blocked at[l_1] rval[my. Lock] at[l_C] rval[my. Lock] at[l_0] l_0: while (true) { l_1: synchronized(my. Lock) { l_C: // critical actions l_2: } l_3: }

Concrete Configuration held_by at[l_1] rval[my. Lock] blocked at[l_C] rval[my. Lock] at[l_1] at[l_0] rval[my. Lock] at[l_0]

Abstract Configuration blocked at[l_1] rval[my. Lock] held_by at[l_C] rval[my. Lock] at[l_0]

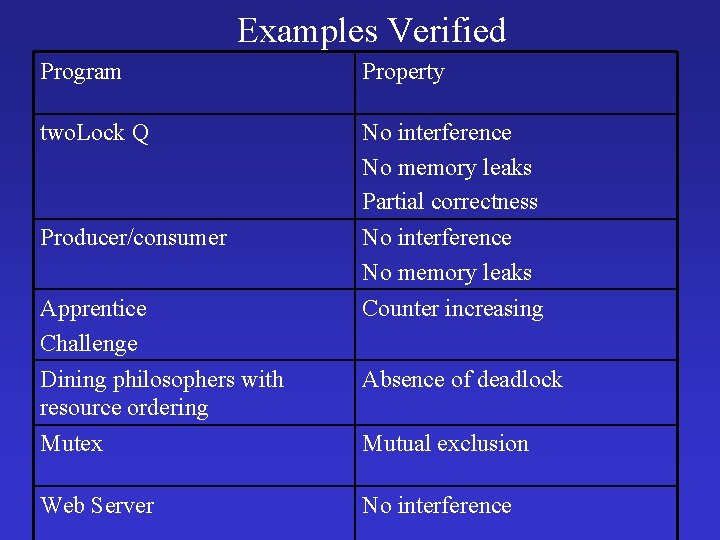
Examples Verified Program Property two. Lock Q No interference No memory leaks Partial correctness Producer/consumer No interference No memory leaks Counter increasing Apprentice Challenge Dining philosophers with resource ordering Mutex Web Server Absence of deadlock Mutual exclusion No interference

Summary • Canonical abstraction guarantees finite number of structures • The concrete location of an object plays no significance • But what is the significance of 3 -valued logic?

Topics • Embedding • Instrumentation • Abstract Interpretation • [Extensions]

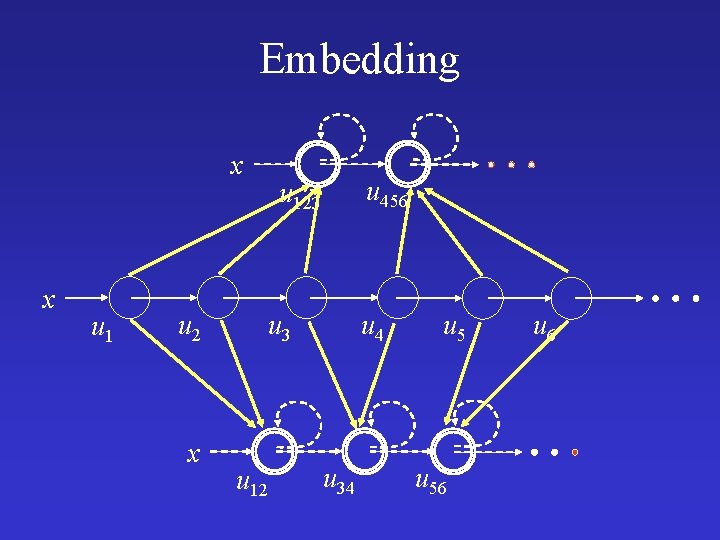
Embedding x x u 1 u 2 x u 456 u 123 u 12 u 4 u 34 u 56 u 6

Embedding • B f S • onto function f • p. B(u 1, . . , uk) p. S (f(u 1), . . . , f(uk)) • S is a tight embedding of B with respect to f if: • p. S(u#1, . . , u#k) = {p. B (u 1. . . , uk) | f(u 1)=u#1, . . . , f(uk)=u#k} • Canonical Abstraction is a tight embedding

Embedding (cont) • S 1 f S 2 every concrete state represented by S 1 is also represented by S 2 • The set of nodes in S 1 and S 2 may be different – No meaning for node names (abstract locations) • (S#)= {S : 2 -valued structure S, S f S#}

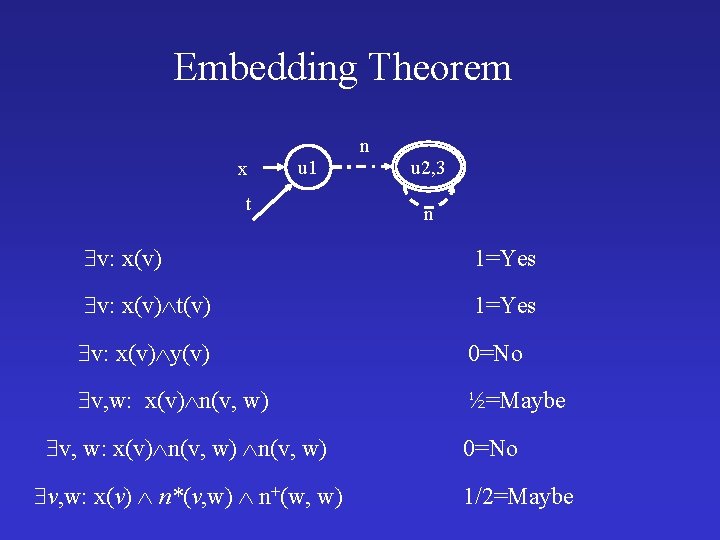
Embedding Theorem • Assume B f S, p. B(u 1, . . , uk) p. S (f(u 1), . . . , f(uk)) • Then every formula is preserved: – If = 1 in S, then = 1 in B – If = 0 in S, then = 0 in B – If = 1/2 in S, then could be 0 or 1 in B

Embedding Theorem • For every formula is preserved: – If = 1 in S, then = 1 for all B (S) – If = 0 in S, then = 0 for all B (S) – If = 1/2 in S, then could be 0 or 1 in (S)

Challenge 2 - Destructive Update x n p y y next = NULL n’(v, w) = y(v) n(v, w) x p y Sound

Challenge 2 - Destructive Update x n p y y next = NULL n’(v, w) = y(v) n(v, w) x p y Sound

Embedding Theorem x u 1 t n u 2, 3 n v: x(v) 1=Yes v: x(v) t(v) 1=Yes v: x(v) y(v) 0=No v, w: x(v) n(v, w) ½=Maybe v, w: x(v) n(v, w) v, w: x(v) n*(v, w) n+(w, w) 0=No 1/2=Maybe

Summary • The embedding theorem eliminates the need for proving near commutavity • Guarantees soundness • Applied to arbitrary logics • But can be imprecise

Limitations • Information on summary nodes is lost • Leads to useless verification

Increasing Precision • User (Programming Language) supplied global invariants – Naturally expressed in FOTC • Record extra information in the concrete interpretation – Tune the abstraction – Refine concretization

Cyclicity predicate c[x]() = v 1, v 2: x(v 1) n*(v 1, v 2) n+(v 2, v 2) c[x]()=0 u 1 x t c[x]()=0 x t n u 2 u 1 n n … n u 2. . n n un

Cyclicity predicate c[x]() = v 1, v 2: x(v 1) n*(v 1, v 2) n+(v 2, v 2) n c[x]()=1 u 1 n x u 2 n t c[x]()=1 x t u 1 n … n u 2. . n n un

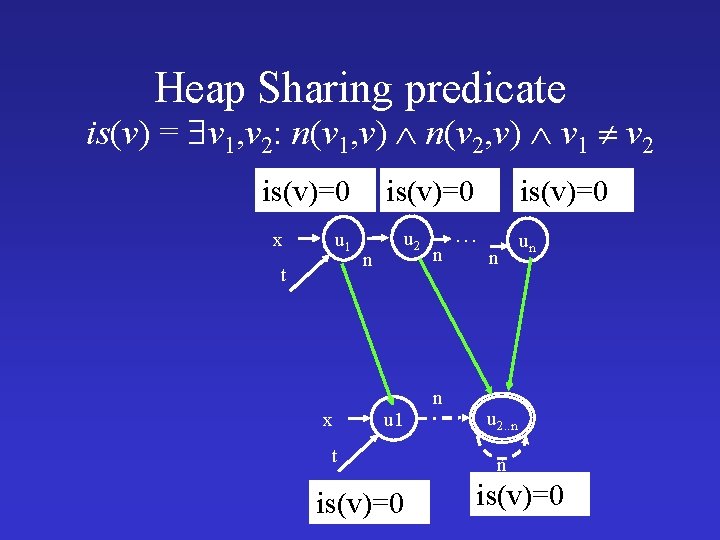
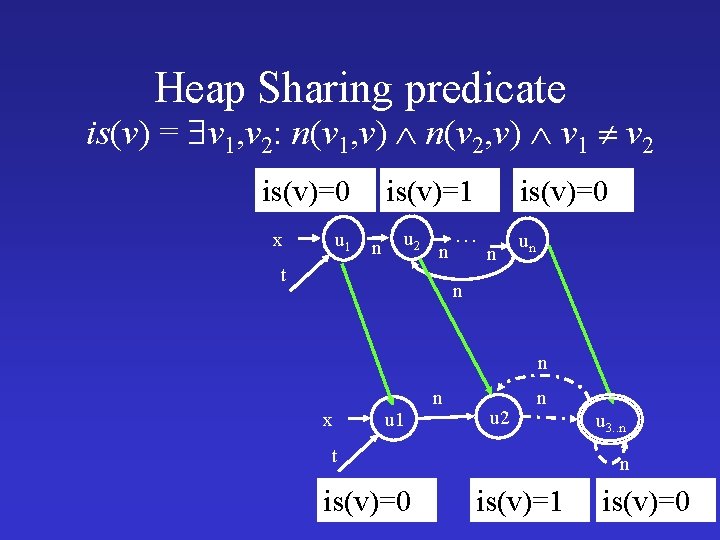
Heap Sharing predicate is(v) = v 1, v 2: n(v 1, v) n(v 2, v) v 1 v 2 is(v)=0 u 1 x t x is(v)=0 n u 2 u 1 t is(v)=0 n n is(v)=0 … n un u 2. . n n is(v)=0

Heap Sharing predicate is(v) = v 1, v 2: n(v 1, v) n(v 2, v) v 1 v 2 is(v)=0 u 1 n x is(v)=1 u 2 n t is(v)=0 … n un n n x u 1 n u 2 n t is(v)=0 u 3. . n n is(v)=1 is(v)=0

Concrete Interpretation Rules Statement Update formula x =NULL x’(v)= 0 x= malloc() x’(v) = Is. New(v) x=y x’(v)= y(v) x=y next x’(v)= w: y(w) n(w, v) x next=NULL n’(v, w) = x(v) n(v, w) is’(v) = is(v) v 1, v 2: n(v 1, v) n(v 2, v) x(v 1) x(v 2) eq(v 1, v 2)

Reachability predicate t[n](v 1, v 2) = n*(v 1, v 2) x t[n] u 1 u 2 t n t[n] n un n t[n] x t u 1 t[n] n u 2. . n n t[n]

Additional Instrumentation predicates • • • reachable-from-variable-x(v) cfb(v) = v 1: f(v, v 1) b(v 1, v) tree(v) dag(v) in. Order(v) = v 1: n(v, v 1) dle(v, v 1) • Weakest Precondition [Ramalingam PLDI 02]

Instrumentation (Summary) • Refines the abstraction is(v) = v 1, v 2: n(v 1, v) n(v 2, v) v 1 v 2 • Adds global invariants is(v) v 1, v 2: n(v 1, v) n(v 2, v) v 1 v 2 (S#)={S : S , S f S#} • But requires update-formulas (generated automatically in TVLA 2

Plan • Embedding Theorem • Instrumentation • Abstract interpretation using canonical abstraction • TVLA

Best Conservative Interpretation (CC 79) Concrete Representation Concretization Abstract Interpretation Collecting Interpretation st # st c Concrete Representation Abstraction Abstract Representation

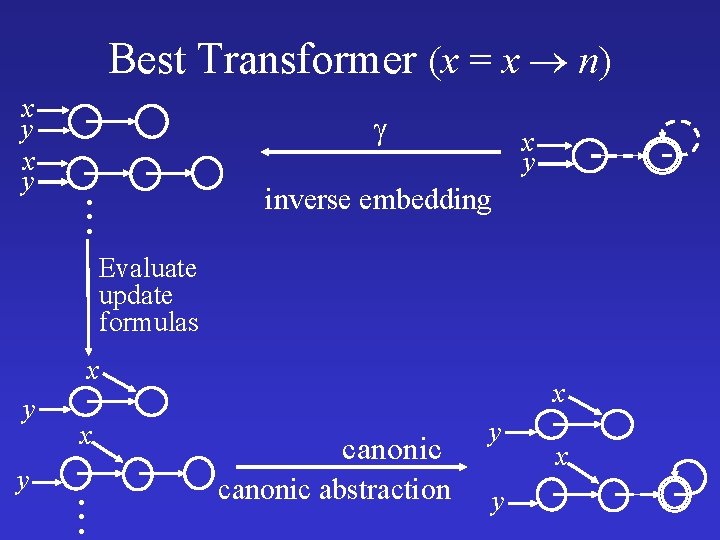
Best Transformer (x = x n) x y . . . x y inverse embedding Evaluate update formulas x y y x . . . x canonic abstraction y y x

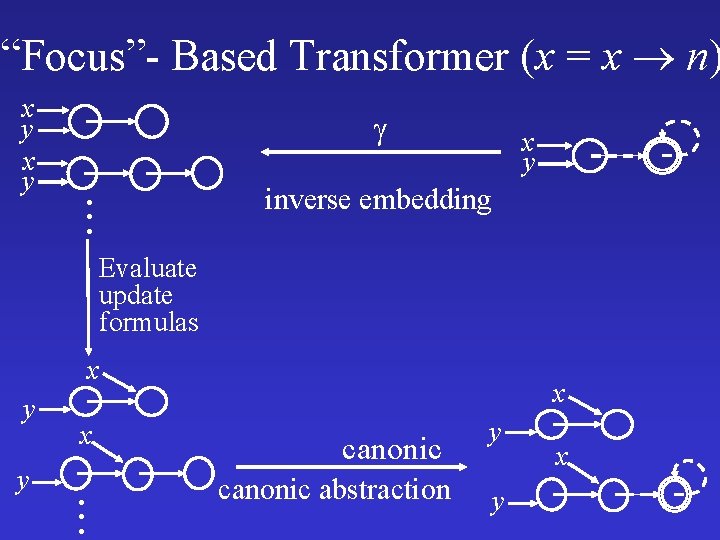
“Focus”- Based Transformer (x = x n) x y . . . x y inverse embedding Evaluate update formulas x y y x . . . x canonic abstraction y y x

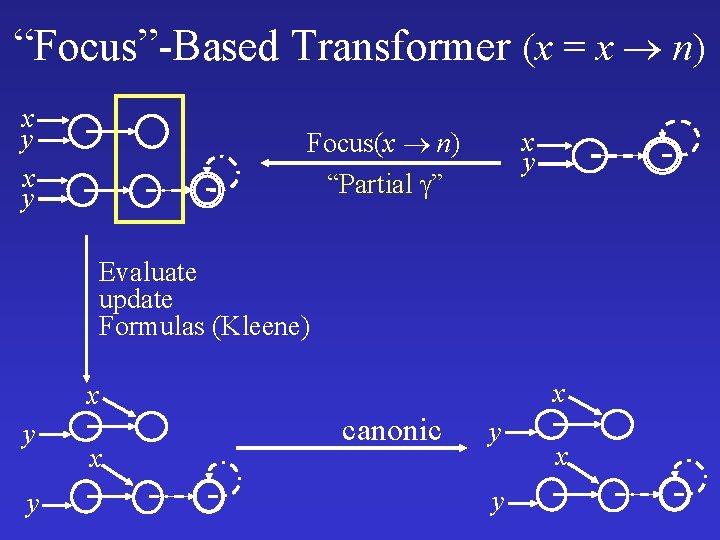
“Focus”-Based Transformer (x = x n) x y Focus(x n) “Partial ” x y Evaluate update Formulas (Kleene) x x y y x canonic y y x

Semantic Reduction • Improve the precision by recovering properties of the program semantics • A Galois connection (L 1, , , L 2) • An operation op: L 2 is a semantic reduction – l L 2 op(l) l – (op(l)) = (l) • Can be applied before and after basic operations L 1 L 2 l op

Three Valued Logic Analysis (TVLA) T. Lev-Ami & R. Manevich • Input (FOTC) – – Concrete interpretation rules Definition of instrumentation predicates Definition of safety properties First Order Transition System (TVP) • Output – Warnings (text) – The 3 -valued structure at every node (invariants)

Null Dereferences typedef struct element { int value; struct element n; } Element Demo bool search( int value, Element x) { Element c = x while ( x != NULL ) { if (c val == value) return TRUE; c = c n; } 40 return FALSE; }

TVLA inputs TVP - Three Valued Program – Predicate declaration – Action definitions SOS – Control flow graph Program independent • TVS - Three Valued Structure Demo

Challenge 1 • Write a C procedure on which TVLA reports false null dereference

Proving Correctness of Sorting Implementations (Lev-Ami, Reps, S, Wilhelm ISSTA 2000) • Partial correctness – The elements are sorted – The list is a permutation of the original list • Termination – At every loop iterations the set of elements reachable from the head is decreased

Example: Insert. Sort typedef struct list_cell { int data; struct list_cell *n; } *List; pred. tvp actions. tvp Run Demo List Insert. Sort(List x) { List r, pr, rn, l, pl; r = x; pr = NULL; while (r != NULL) { l = x; rn = r n; pl = NULL; while (l != r) { if (l data > r data) { pr n = rn; r n = l; if (pl = = NULL) x = r; else pl n = r; r = pr; break; } pl = l; l = l n; } pr = r; r = rn; } return x; }

Example: Insert. Sort typedef struct list_cell { int data; struct list_cell *n; } *List; Run Demo List Insert. Sort(List x) { if (x == NULL) return NULL pr = x; r = x->n; while (r != NULL) { pl = x; rn = r->n; l = x->n; while (l != r) { pr->n = rn ; r->n = l; pl->n = r; r = pr; break; } pl = l; l = l->n; } pr = r; r = rn; } 14

Example: Reverse typedef struct list_cell { int data; struct list_cell *n; } *List; Run Demo List reverse (List x) { List y, t; y = NULL; while (x != NULL) { t = y; y = x; x = x next; y next = t; } return y; }

Challenge • Write a sorting C procedure on which TVLA fails to prove sortedness or permutation

Example: Mark and Sweep void Mark(Node root) { if (root != NULL) { pending = pending {root} marked = while (pending ) { x = Select. And. Remove(pending) marked = marked {x} t = x left if (t NULL) if (t marked) pending = pending {t} t = x right if (t NULL) if (t marked) pending = pending {t} } } assert(marked = = Reachset(root)) } void Sweep() { unexplored = Universe collected = while (unexplored ) { x = Select. And. Remove(unexplored) if (x marked) collected = collected {x} } assert(collected = = Universe – Reachset(root) ) } pred. tvp Run Demo

Challenge 2 • Use TVLA to show termination of mark. And. Sweep

Verification of Safety Properties (PLDI’ 02, 04) The Canvas Project (with IBM Watson) (Component Annotation, Verification and Stuff) Component a library with cleanly encapsulated state Lightweight Specification §"correct usage" rules a client must follow §"call open() before read()" Client a program that uses the library Certification does the client program satisfy the lightweight specification?

Prototype Implementation • Applied to several example programs – Up to 5000 lines of Java • Used to verify – Absence of concurrent modification exception – JDBC API conformance – IOStreams API conformance

Scaling • Staged analysis • Controlled complexity – More coarse abstractions [Manevich SAS’ 04] • Handle libraries – Use procedure specifications [Yorsh, TACAS’ 04] – Decision procedures for linked data structures [Immerman, CAV’ 04, Lev-Ami, CADE’ 05] • Handling procedures – Compute procedure summaries [Jeannet, SAS’ 04] – Local heaps [Rinetzky, POPL’ 05]

Local heaps [Rinetzky, POPL’ 05] x x y call p(x); y g g t t

Why is Heap Analysis Difficult? • Destructive updating through pointers – p next = q – Produces complicated aliasing relationships – Track aliasing on 3 -valued structures • Dynamic storage allocation – No bound on the size of run-time data structures – Canonical abstraction finite-sized 3 -valued structures • Data-structure invariants typically only hold at the beginning and end of operations – Need to verify that data-structure invariants are reestablished – Query the 3 -valued structures that arise at the exit

Summary • Canonical abstraction is powerful – Intuitive – Adapts to the property of interest • Used to verify interesting program properties – Very few false alarms • But scaling is an issue

Summary • Effective Abstract Interpretation – Always terminates – Precise enough – But still expensive • Can model – Heap – Unbounded arrays – Concurrency • More instrumentation can mean more efficient • But canonic abstraction is limited – Correlation between list lengths – Arithmetic – Partial heaps

Summary • The embedding theorem eliminates the need for proving near commutavity • Guarantees soundness • Applied to arbitrary logics • But can be imprecise