REGRESSION SHRINKAGE AND SELECTION VIA THE LASSO Author

REGRESSION SHRINKAGE AND SELECTION VIA THE LASSO Author: Robert Tibshirani Journal of the Royal Statistical Society 1996 1 Presentation: Tinglin Liu Oct. 27 2010

OUTLINE What’s the Lasso? Why should we use the Lasso? Why will the results of Lasso be sparse? How to find the Lasso solutions? 2

OUTLINE What’s the Lasso? Why should we use the Lasso? Why will the results of Lasso be sparse? How to find the Lasso solutions? 3

LASSO(LEAST ABSOLUTE SHRINKAGE AND SELECTION OPERATOR) Definition It’s a coefficients shrunken version of the ordinary Least Square Estimate, by minimizing the Residual Sum of Squares subjecting to the constraint that the sum of the absolute value of the coefficients should be no greater than a constant. 4

LASSO(LEAST ABSOLUTE SHRINKAGE AND SELECTION OPERATOR) Features Equivalent to the Classic Expression of Sparse Coding Here, the standardization is required to make the normalize every predictor variable. and Murray, W. , Gill, P. and Wright, M. (1981) Practical Optimization. Chapter 5. Academic Press 5

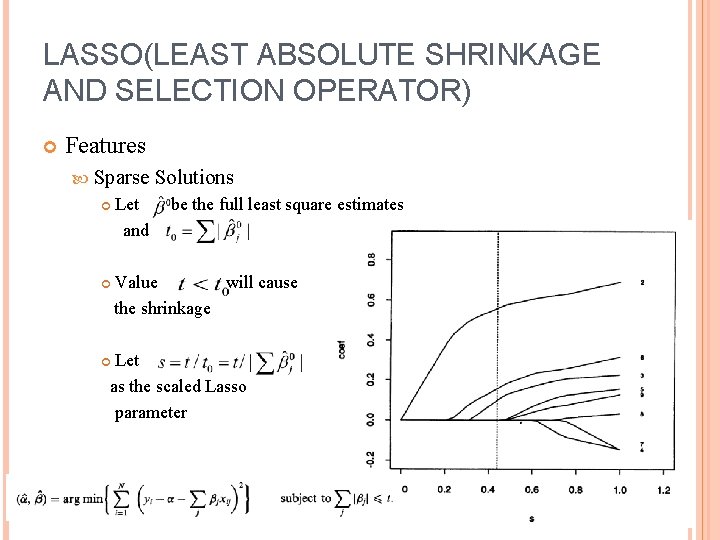
LASSO(LEAST ABSOLUTE SHRINKAGE AND SELECTION OPERATOR) Features Sparse Let and Solutions be the full least square estimates Value will cause the shrinkage Let as the scaled Lasso parameter 6

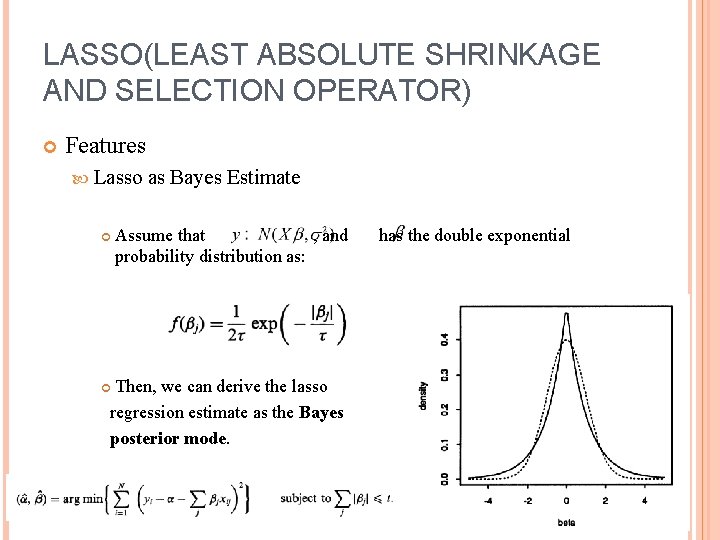
LASSO(LEAST ABSOLUTE SHRINKAGE AND SELECTION OPERATOR) Features Lasso as Bayes Estimate Assume that , and probability distribution as: has the double exponential Then, we can derive the lasso regression estimate as the Bayes posterior mode. 7

OUTLINE What’s the Lasso? Why should we use the Lasso? Why will the results of Lasso be sparse? How to find the Lasso solutions? 8

WHY LASSO? Prediction Accuracy Assume , and , then the prediction error of the estimate is OLS estimates often have low bias but large variance, the Lasso can improve the overall prediction accuracy by sacrifice a little bias to reduce the variance of the predicted value. 9

WHY LASSO? Interpretation In many cases, the response is determined by just a small subset of the predictor variables. 10

OUTLINE What’s the Lasso? Why should we use the Lasso? Why will the results of Lasso be sparse? How to find the Lasso solutions? 11

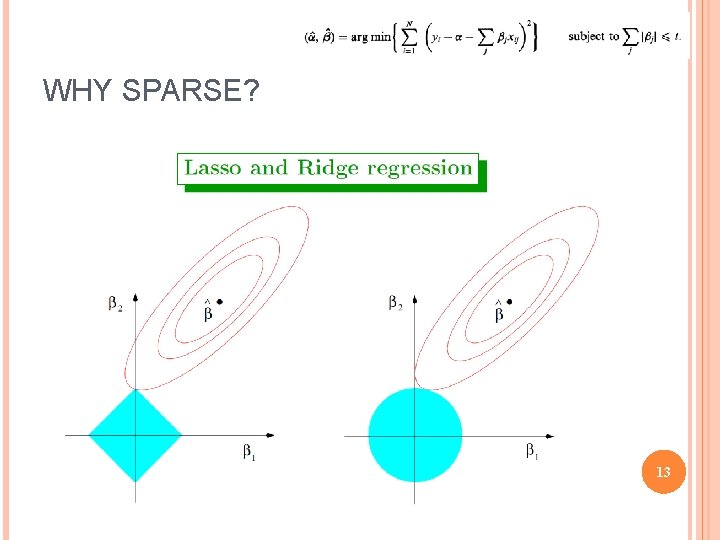
WHY SPARSE? Geometry of Lasso The criterion equals to the quadratic function as: This function is expressed as the elliptical contour centered at the OLS estimates. The L 1 norm constraints centered at the origin. is expressed as the square The Lasso solution is the first place where the contour touches the square. 12

WHY SPARSE? 13

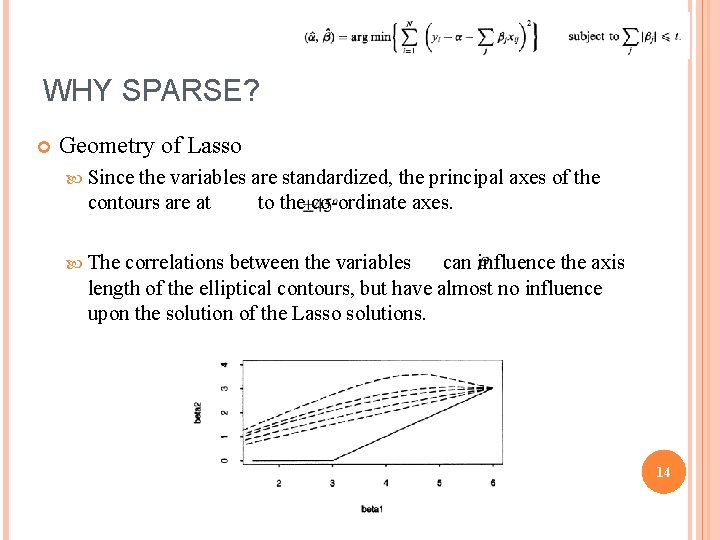
WHY SPARSE? Geometry of Lasso Since the variables are standardized, the principal axes of the contours are at to the co-ordinate axes. The correlations between the variables can influence the axis length of the elliptical contours, but have almost no influence upon the solution of the Lasso solutions. 14

OUTLINE What’s the Lasso? Why should we use the Lasso? Why will the results of Lasso be sparse? How to find the Lasso solutions? 15

HOW TO SOLVE THE PROBLEM? The absolute inequality constraints can be translated into inequality constraints. ( p stands for the number of predictor variables ) Where is an constraints. matrix, corresponding to linear inequality But direct application of this procedure is not practical due to the fact that may be very large. Lawson, C. and Hansen, R. (1974) Solving Least Squares Problems. Prentice Hall. 16

HOW TO SOLVE THE PROBLEM? Outline of the Algorithm Sequentially introduce the inequality constraints In practice, the average iteration steps required is in the range of (0. 5 p, 0, 75 p), so the algorithm is acceptable. Lawson, C. and Hansen, R. (1974) Solving Least Squares Problems. Prentice Hall. 17

18