Output Sensitive Enumeration 6 Isomorphism Rootedtree Tree Floorplan

Output Sensitive Enumeration 6. Isomorphism Rooted-tree, Tree, Floorplan • • • Necklace Rooted Tree Non-rooted trees Colored Trees Floorplans Other Geometric Objects

Graph Enumeration • Previous enumeration problems aim to enumerate “substructures” of the given instances (ex. paths in a graph) • On the other hand, there is a problem of finding “all structures” in the given specified class (ex, matrices) • For some classes, the problem is trivial + paths, cycles: lengths of 1, 2, … + cliques: sizes of 1, 2, … + permutations of size n • For some classes, the problem is non-trivial + trees, crossing lines (in plane), matriods, 01 -matrices…

Isomorphism • On non-trivial structures, we have to take care of “isomorphism” Isomorphism: a structure is isomorphic to another if there is oneto-one correspondence between the elements with keeping some condition + a ring sequence (necklace) is isomorphic to another iff it can be transformed to another by rotation + a matrix is isomorphic to another iff it can be transformed to the other by swapping rows, and swapping columns + a graph is isomorphic to another iff there is a one to one mapping between vertices preserving the adjacency Enumerate all structures so that no two are isomorphic

6 -1 Necklace Enumeration

Problem Definition • Necklace is a cyclic string, in that the first and last letters are adjacent ABCDEA E C D A B B E A CDEABC C D EABCD • Complete enumeration of necklace, of length n with alphabet Σ is easy; just enumerate all the strings of length n • However several (n) strings give the same necklace, so we have duplicates…

Avoiding Duplicates • A typical way to avoiding the duplications is store all the solutions in memory, ABABA check the existence for each new solution A B C D E • For checking the existence, we rotate the query string in n ways; so we have to issue n queries • If we prepare all the rotations of strings in the data, we need only 1 query FFFCC DDDDD ABACD ? On the other hand, memory consumption increases with factor of n

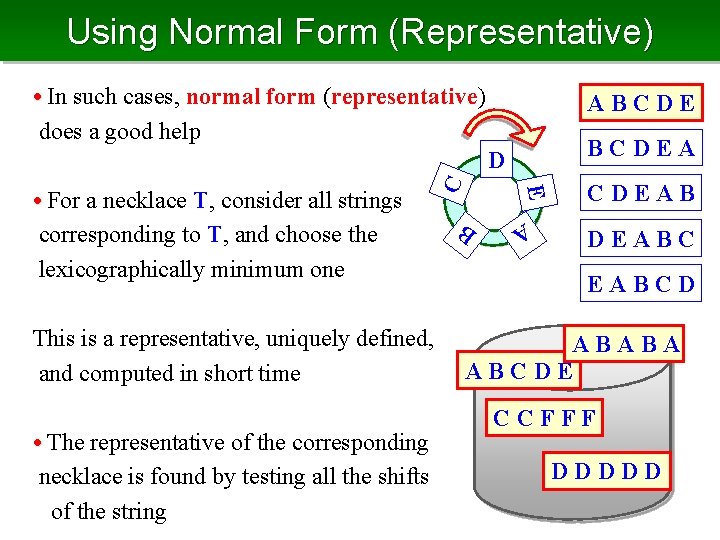
Using Normal Form (Representative) • In such cases, normal form (representative) does a good help ABCDEA B • The representative of the corresponding necklace is found by testing all the shifts of the string A This is a representative, uniquely defined, and computed in short time E • For a necklace T, consider all strings corresponding to T, and choose the lexicographically minimum one C D CDEABC EABCD ABABA ABCDE CCFFF DDDDD

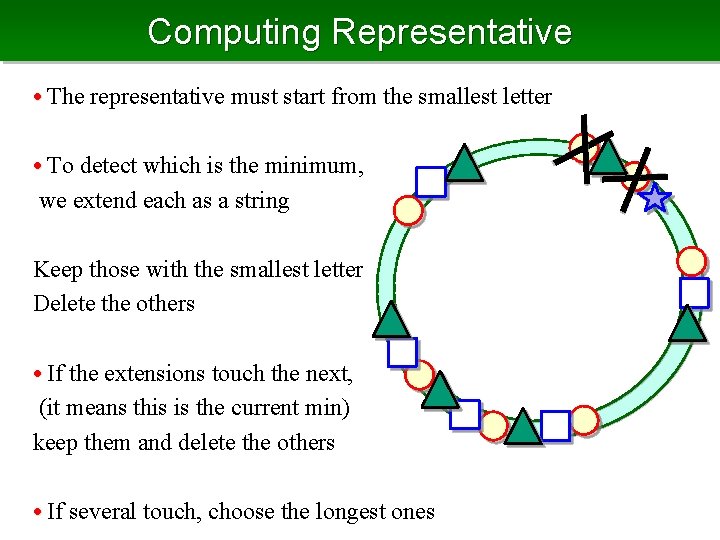
Computing Representative • The representative must start from the smallest letter • To detect which is the minimum, we extend each as a string Keep those with the smallest letter Delete the others • If the extensions touch the next, (it means this is the current min) keep them and delete the others • If several touch, choose the longest ones

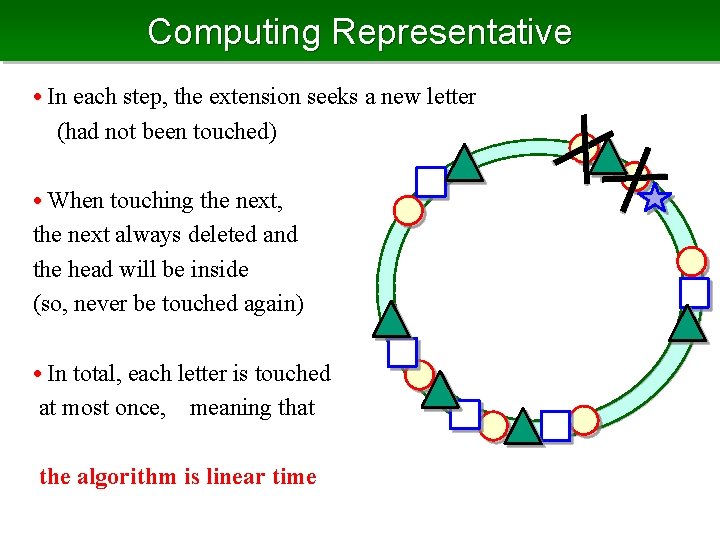
Computing Representative • In each step, the extension seeks a new letter (had not been touched) • When touching the next, the next always deleted and the head will be inside (so, never be touched again) • In total, each letter is touched at most once, meaning that the algorithm is linear time

Avoiding with Representative • Enumerate all the strings of length n Compute the representative of each, and store in memory (a database) • Then, for checking the existence, we have to have only one query • O(n) time to + get representative + store one representative + check one existence query ABABA ABCDE FFFCC DDDDD ABACD ?

Depth-First Way • …Actually, with representative, the storage for solutions becomes not necessary Just enumerate all strings of length n, and output them only when they are being representatives ABABA ABCDE FFFCC • O(n) time to + get representative without storage, so polynomial memory space DDDDD

Enumerate Representatives, Directly • …Then, we are naturally motivated to enumerate only representatives Then, there would be no time consuming Problems ABABA ABCDE But, simple enumeration finds all strings, so we need some modifications on string enumeration FFFCC DDDDD

Representative Enumeration ABCDEFGH • The first letter has to be smallest • If there are some smallest letters, the prefix of k letters must be always smallest among all substrings of length k Observation For any representative, changing the last “non-biggest” (say, Z) letter to the “biggest letter” (Z) yields also a representative We can enumerate all representatives by + starting from ZZZZZ…Z, and + changing some Z having no non-Z latter, iteratively ABCABCBB ABZAZZZZ

Redundancy + starting from ZZZZZ…Z, and + changing some Z having no non-Z latter, iteratively ↑ This is complete so we can enumerate ABCDEZZZ Enum. Necklace (S) 1. output S 2. for each i s, t, S[i] = Z, no j > i satisfies S[j] ≠ Z 3. for each letter a ≥ S[1], 4. S[i] : = a 5. if S is representative then call Enum. Necklace (S) 6. end for 7. S[i] : = Z 8. end for

Conditions to be Representatives ABCDEFGH • The check for being representative is a cost Consider some good conditions to be representative necessary • The first letter has to be smallest • If there are some smallest letters, the prefix of k letters must be always smallest among all substrings of length k • For a representative S, + change Z to a < S[1] is always bad always a < head + change Z to a > S[1] is always good, if S is not repetitive • If S is partially repetitive, there are several cases ABCABCABCZZ

Handling Repetition • S[1. . i-1] is repetitive a substring ending at S[i-1] = prefix of S • When “no substring ending at S[i-1] = prefix of S” + change Z to a > S[1] is always good prefix of S is always smaller than any other ending at S[i], and all letters after S[i] are “Z” ABCABCABFZZZ • If S is repetitive, some are good and some are bad

Handling Repetition • S[1. . i-1] is repetitive a substring ending at S[i-1] = prefix of S • When S is repetitive, + change Z to a < S[j] is always bad, and a ≥ S[j] is always good change Z to a < S[j] yields that the repeat substring will be smaller than the prefix change Z to a ≥ S[j] keeps that the prefix is still the smallest j ABCABCABZZZ

Multiple Repetitions • S[1. . i-1] is repetitive a substring ending at S[i-1] = prefix of S • When S is multiply repetitive, for all same substrings, the same statement holds change Z to a ≥ S[j] keeps that the prefix is still the smallest ABCDABCDABZZZZ

Copy Position • For position i, define copy position copy(S, i) by smallest j s. t. S[1. . j] = S[i-j. . i-1] (by 0 if no j satisfies it) by changing S[i] to a, S is still representative if and only if a ≥ S[j] So, by maintaining the copy position during the computation, we can easily generate only representatives ABCDABCDABZZZZ

Algorithm with Copy Position changing S[i] to a, S gives a representative a ≥ S[copy(S, i)] Enum. Necklace (S) 1. output S 2. for each i s, t, S[i] = Z, no j > i satisfies S[j] ≠ Z 3. compute copy(S, i) 4. for each letter a ≥ S[copy(S, i)], 4. S[i] : = a 5. call Enum. Necklace (S) 6. end for No check is 7. S[i] : = Z necessary 8. end for

Maintaining Copy Position copy(S, i+1) = copy(S, i) if S[copy(S, i)] = Z 0 otherwise • By changing S[i] to a (≥ S[copy(S, i)]) copy(S, i+1) changes to so easy to be maintained in O(1) time copy(S, i) if S[copy(S, i)] = a 0 otherwise ABCDABCDABZ Z

6 -2 Reverse Search for Ordered Trees

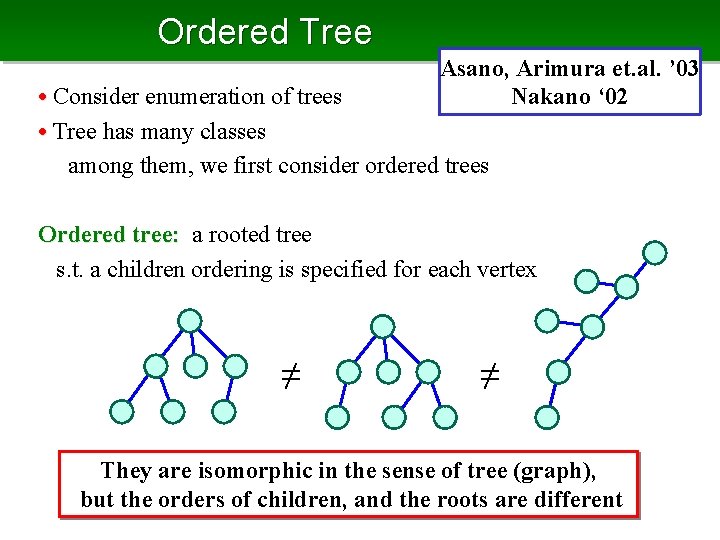
Ordered Tree Asano, Arimura et. al. ’ 03 Nakano ‘ 02 • Consider enumeration of trees • Tree has many classes among them, we first consider ordered trees Ordered tree: a rooted tree s. t. a children ordering is specified for each vertex ≠ ≠ They are isomorphic in the sense of tree (graph), but the orders of children, and the roots are different

Ambiguity on Representation • Trees (graphs) are represented by combination of sets, thus we need to put indices to vertices (in the case of data structure, same) • It results ambiguity on the representation there are many ways to put indices • By putting the indices in a unique way, or representing by other objects, we can avoid the ambiguity

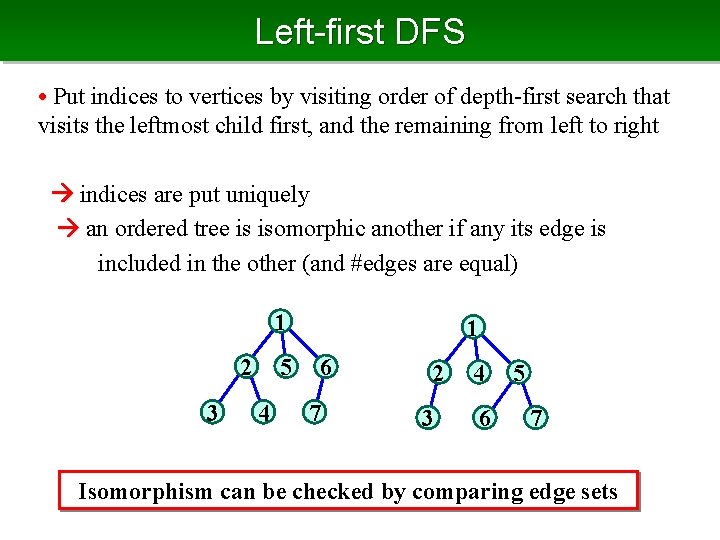
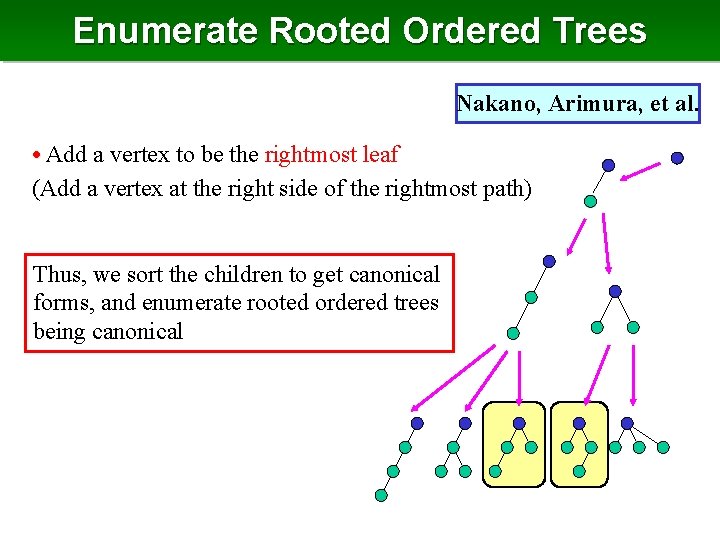
Left-first DFS • Put indices to vertices by visiting order of depth-first search that visits the leftmost child first, and the remaining from left to right indices are put uniquely an ordered tree is isomorphic another if any its edge is included in the other (and #edges are equal) 1 2 3 5 4 1 6 7 2 3 4 6 5 7 Isomorphism can be checked by comparing edge sets

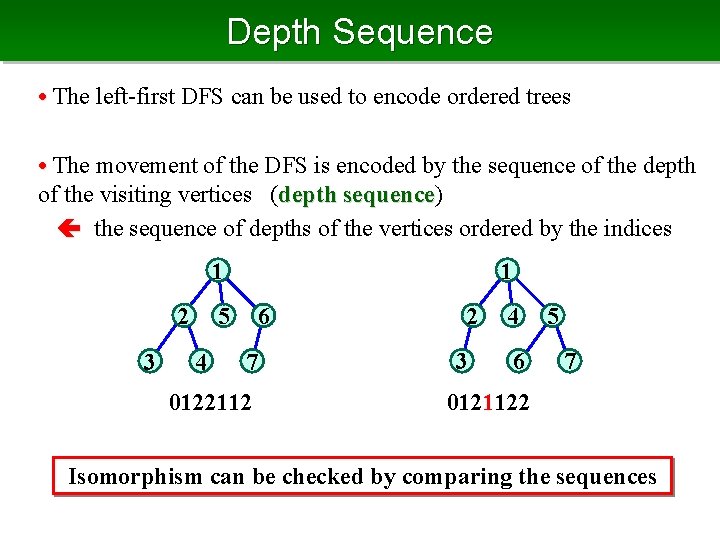
Depth Sequence • The left-first DFS can be used to encode ordered trees • The movement of the DFS is encoded by the sequence of the depth of the visiting vertices (depth sequence) sequence the sequence of depths of the vertices ordered by the indices 1 2 3 1 5 4 6 7 0122112 2 3 4 6 5 7 0121122 Isomorphism can be checked by comparing the sequences

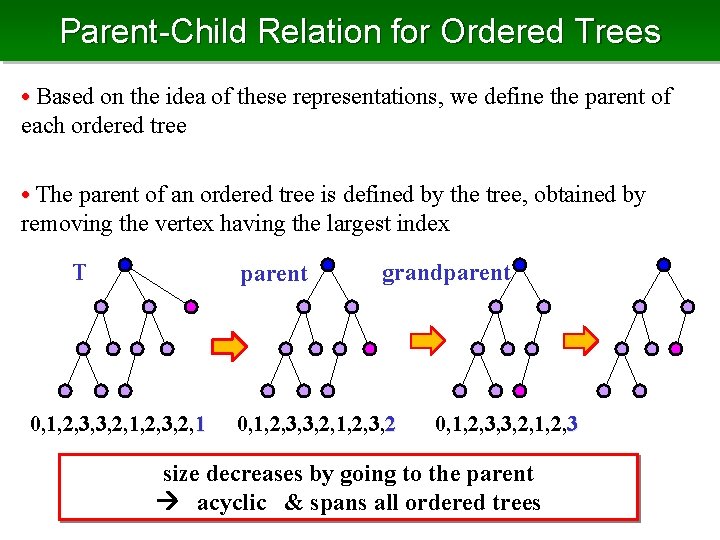
Parent-Child Relation for Ordered Trees • Based on the idea of these representations, we define the parent of each ordered tree • The parent of an ordered tree is defined by the tree, obtained by removing the vertex having the largest index T parent 0, 1, 2, 3, 3, 2, 1, 2, 3, 2, 1 grandparent 0, 1, 2, 3, 3, 2, 1, 2, 3, 2 0, 1, 2, 3, 3, 2, 1, 2, 3 size decreases by going to the parent acyclic & spans all ordered trees

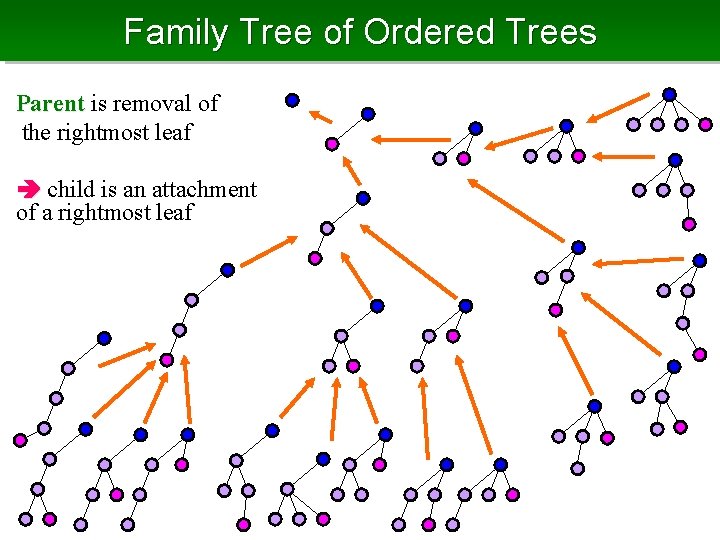
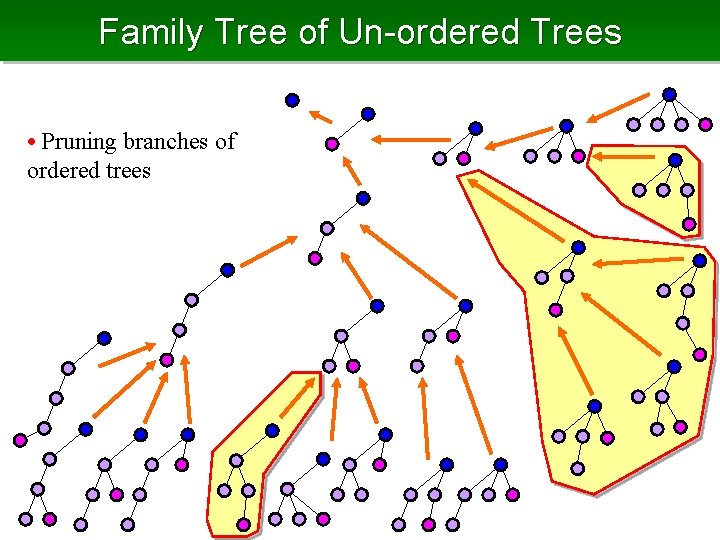
Family Tree of Ordered Trees Parent is removal of the rightmost leaf child is an attachment of a rightmost leaf

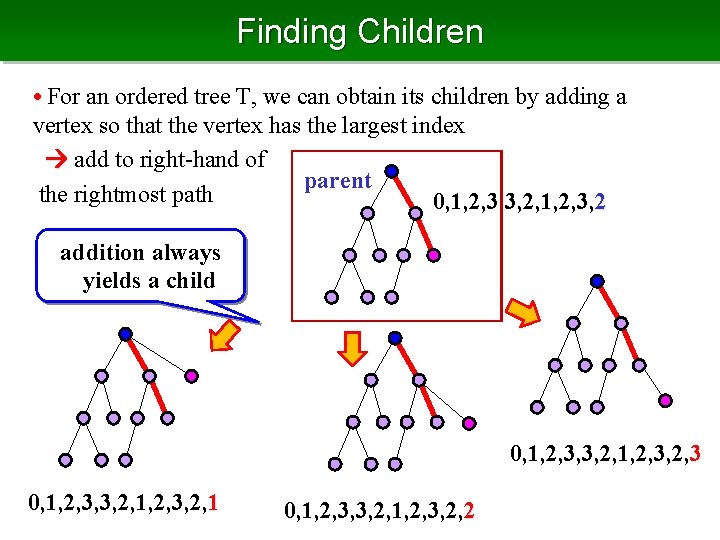
Finding Children • For an ordered tree T, we can obtain its children by adding a vertex so that the vertex has the largest index add to right-hand of parent the rightmost path 0, 1, 2, 3, 3, 2, 1, 2, 3, 2 addition always yields a child 0, 1, 2, 3, 3, 2, 1, 2, 3, 2, 1 0, 1, 2, 3, 3, 2, 1, 2, 3, 2, 2

Pseudo Code • By giving the size limitation, we can enumerate all ordered trees of size less than the specified number k Enum. Ordered. Tree (T) 1. output T 2. if (size of T) = k then return 3. for each vertex v in the right most path 4. add a rightmost child to v 5. call Enum. Ordered. Tree (T) 6. remove the child added in 4 7. end for The inside of the for loop takes constant time, thus time is O(1) for each (output by difference from the previous)

6 -3 Reverse Search for Rooted Trees

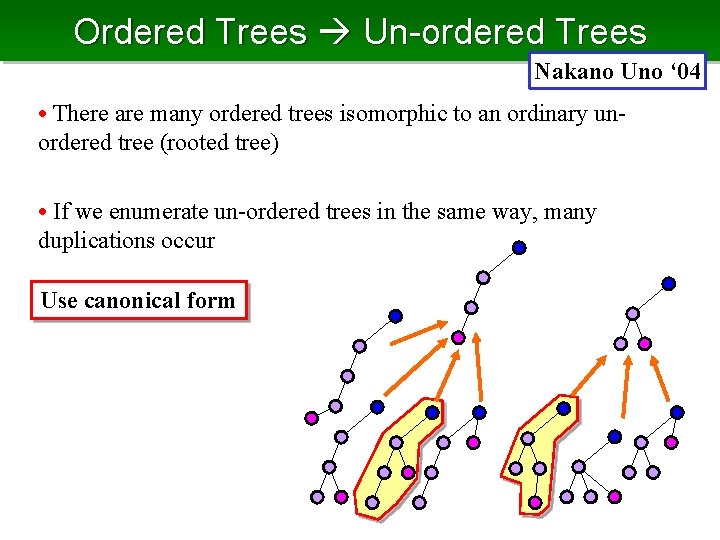
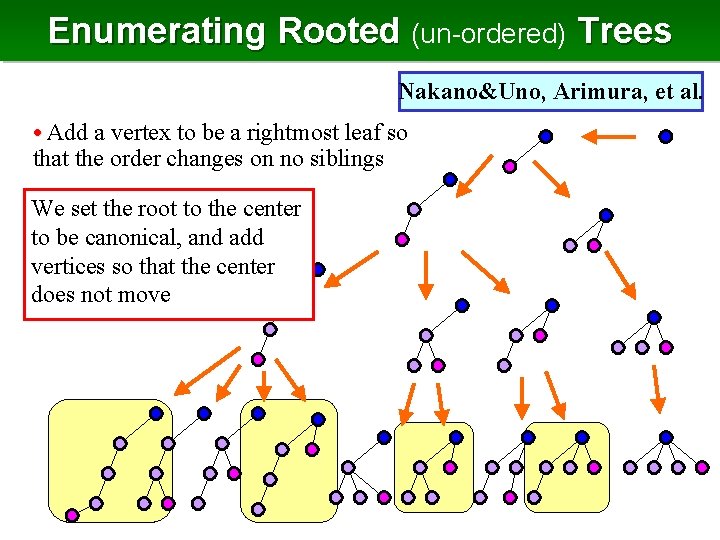
Ordered Trees Un-ordered Trees Nakano Uno ‘ 04 • There are many ordered trees isomorphic to an ordinary unordered tree (rooted tree) • If we enumerate un-ordered trees in the same way, many duplications occur Use canonical form

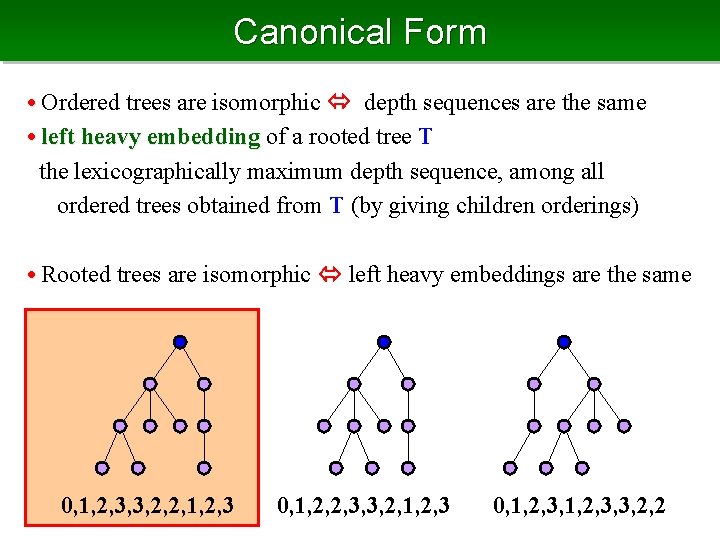
Canonical Form • Ordered trees are isomorphic depth sequences are the same • left heavy embedding of a rooted tree T the lexicographically maximum depth sequence, among all ordered trees obtained from T (by giving children orderings) • Rooted trees are isomorphic left heavy embeddings are the same 0, 1, 2, 3, 3, 2, 2, 1, 2, 3 0, 1, 2, 2, 3, 3, 2, 1, 2, 3 0, 1, 2, 3, 3, 2, 2

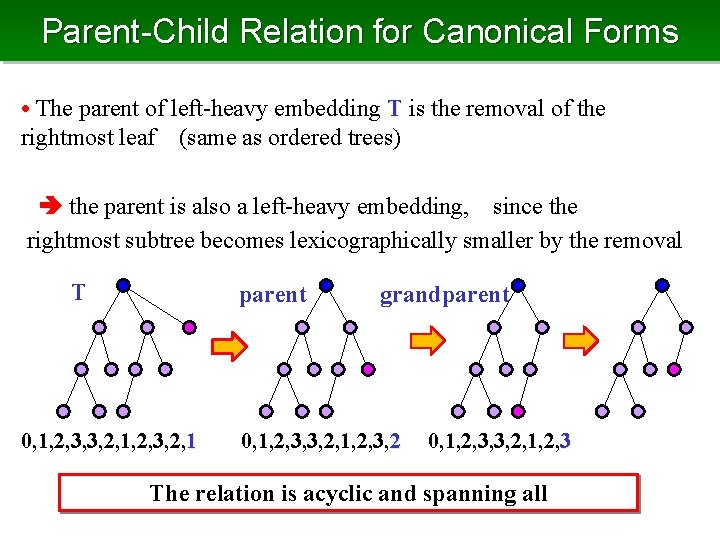
Parent-Child Relation for Canonical Forms • The parent of left-heavy embedding T is the removal of the rightmost leaf (same as ordered trees) the parent is also a left-heavy embedding, since the rightmost subtree becomes lexicographically smaller by the removal T parent 0, 1, 2, 3, 3, 2, 1, 2, 3, 2, 1 grandparent 0, 1, 2, 3, 3, 2, 1, 2, 3, 2 0, 1, 2, 3, 3, 2, 1, 2, 3 The relation is acyclic and spanning all

Family Tree of Un-ordered Trees • Pruning branches of ordered trees

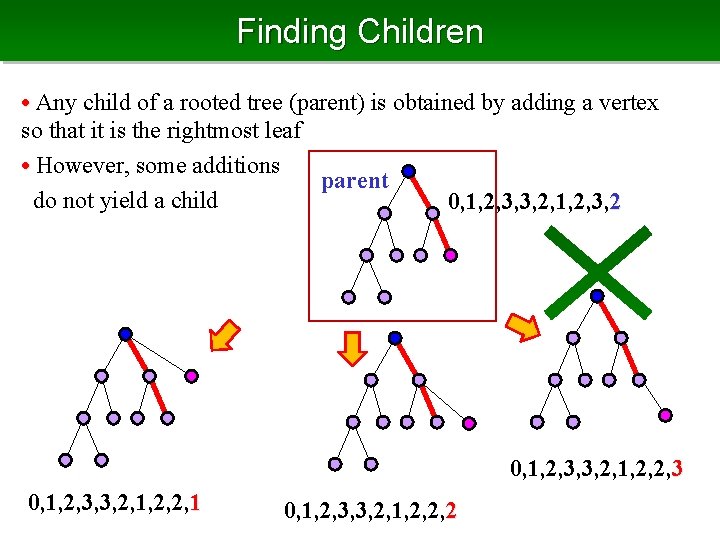
Finding Children • Any child of a rooted tree (parent) is obtained by adding a vertex so that it is the rightmost leaf • However, some additions parent do not yield a child 0, 1, 2, 3, 3, 2, 1, 2, 3, 2 0, 1, 2, 3, 3, 2, 1, 2, 2, 3 0, 1, 2, 3, 3, 2, 1, 2, 2, 1 0, 1, 2, 3, 3, 2, 1, 2, 2, 2

Finding Children • Addition is not a child at some level, right subtree becomes larger than the left • It happens only when the depth sequence of the right is a prefix of that of the left • Below the next depth of the left, no addition yields a child • For all above that, yields a child • We have to take care only the upmost such vertex (being prefix) 34564545 345645 violate only lower prefix corresponding prefix on the left too

Copy Vertex • Copy vertex the upmost vertex s. t. the right subtree is a prefix of the left • Copy vertex changes by the addition of the rightmost leaf. It + does not change if the addition is the same level to the left + becomes to u, if the level is above (u is the parent of the added leaf) 34564545 345645 We can compute copy depth in constant time for each child

Pseudo Code Enum. Rooted. Tree (T, x) 1. output T 2. if the size of T = k then return 3. y : = the vertex next to x in the depth sequence 4. for each v in rightmost path, in increasing order of the depth 5. c : = the rightmost child of v 6. add a rightmost child to v 7. if (depth of v) = (depth of y) then call Enum. Rooted. Tree (T, y); break 8. call Enum. Rooted. Tree (T, c) 9. remove the rightmost child of v 10. end for The inside of the for loop takes O(1) time, thus the time is O(1) for each (output by difference from the previous)

6 -4 Free Trees

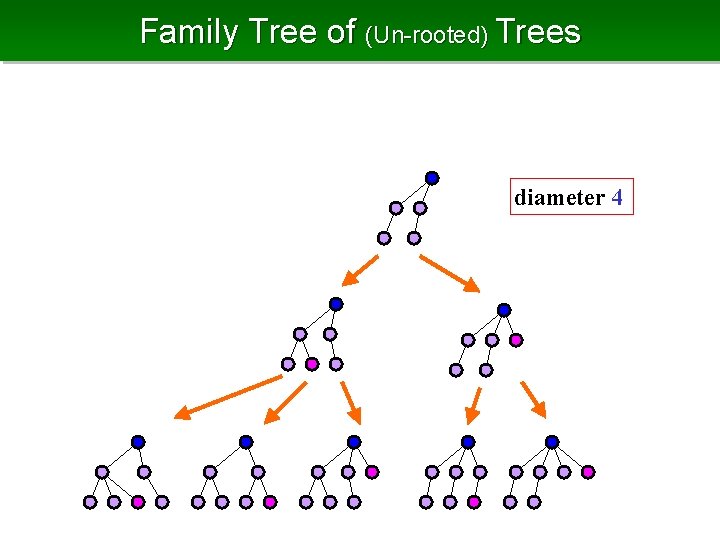
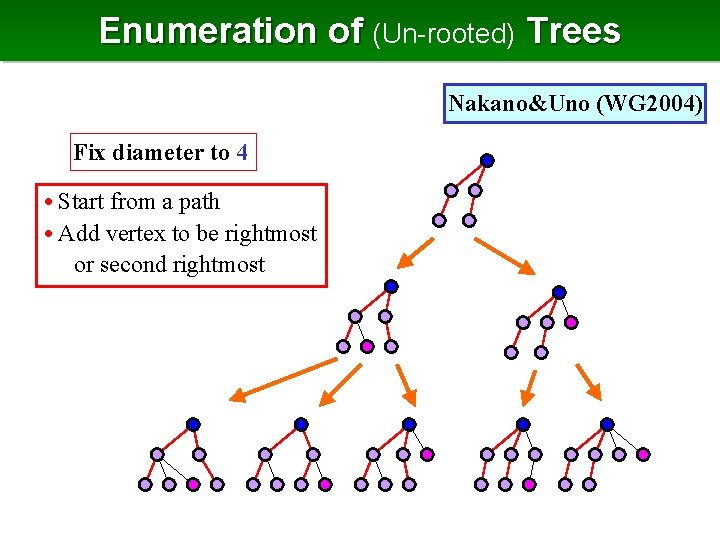
Enumerate Un-rooted Trees • An un-rooted tree has no root, so depth sequence is not defined define the root by its center(s) center Center: Center vertex minimizing the distance to the furthest leaf • The diameter is even the center is unique • We first consider the case of even diameter

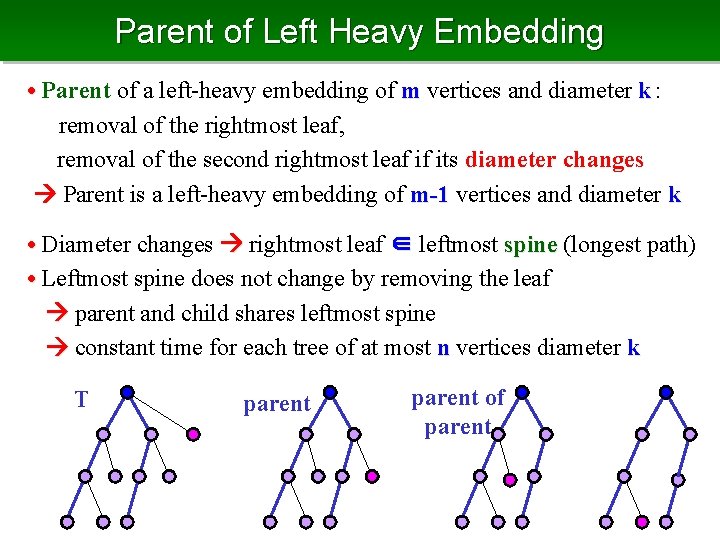
Parent of Left Heavy Embedding • Parent of a left-heavy embedding of m vertices and diameter k： removal of the rightmost leaf, removal of the second rightmost leaf if its diameter changes Parent is a left-heavy embedding of m-1 vertices and diameter k • Diameter changes rightmost leaf ∈ leftmost spine (longest path) • Leftmost spine does not change by removing the leaf parent and child shares leftmost spine constant time for each tree of at most n vertices diameter k T parent of parent

Family Tree of (Un-rooted) Trees diameter 4

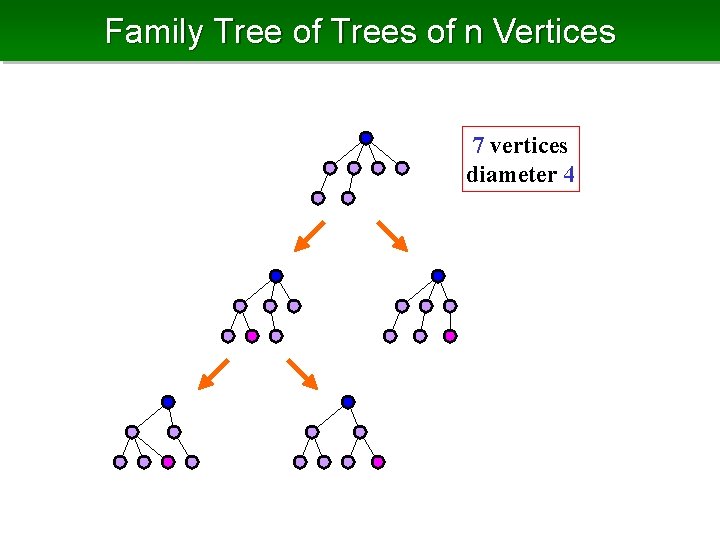
Generating Only Trees of n Vertices Active leaf: rightmost leaf s. t. not a child of root and whose removal does not change the diameter Parent of a left-heavy embedding of n vertices and diameter k : remove active leaf and add a leaf to the root ⇒ also a left-heavy embedding of n vertices and diameter k T parent of parent

Family Tree of Trees of n Vertices 7 vertices diameter 4

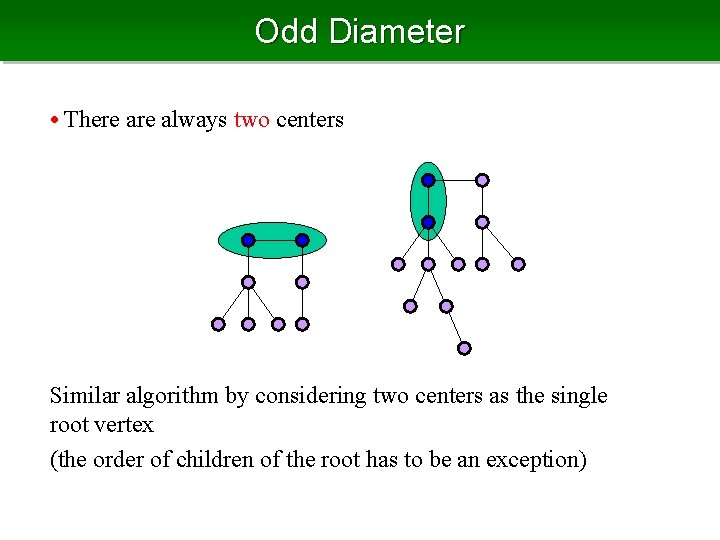
Odd Diameter • There always two centers Similar algorithm by considering two centers as the single root vertex (the order of children of the root has to be an exception)

6 -5 Free Trees and Colored Version

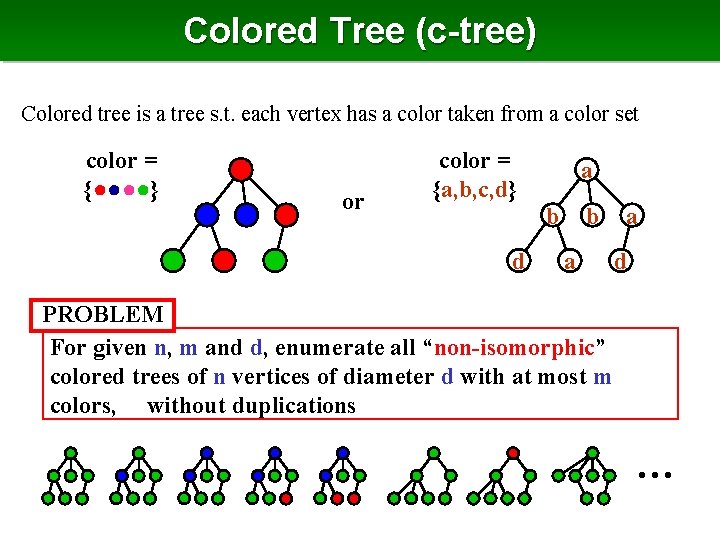
Colored Tree (c-tree) Colored tree is a tree s. t. each vertex has a color taken from a color set color = {●●●●} or color = {a, b, c, d} a b d b a a d PROBLEM For given n, m and d, enumerate all “non-isomorphic” colored trees of n vertices of diameter d with at most m colors, without duplications …

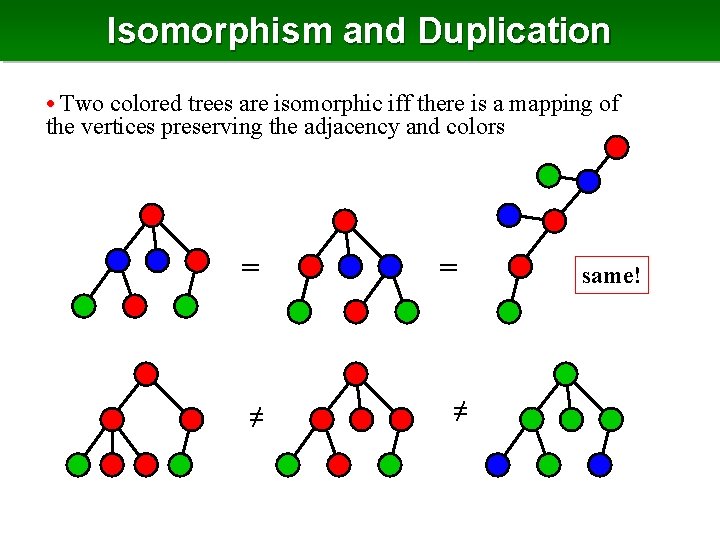
Isomorphism and Duplication • Two colored trees are isomorphic iff there is a mapping of the vertices preserving the adjacency and colors = ≠ same!

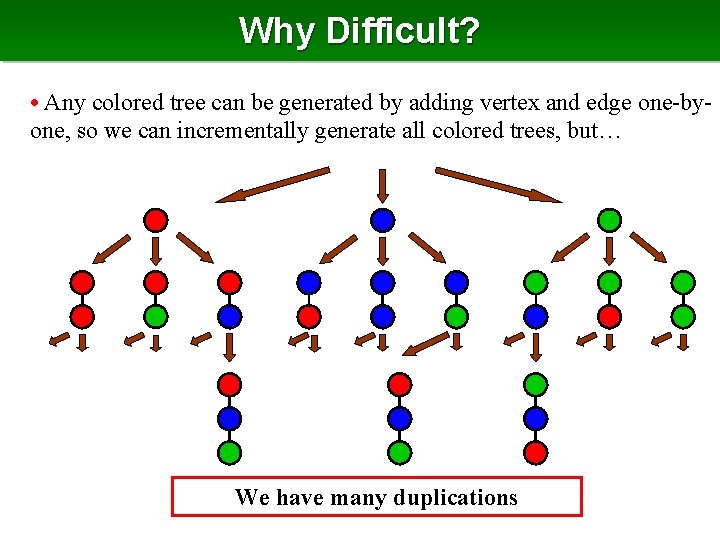
Why Difficult? • Any colored tree can be generated by adding vertex and edge one-byone, so we can incrementally generate all colored trees, but… We have many duplications

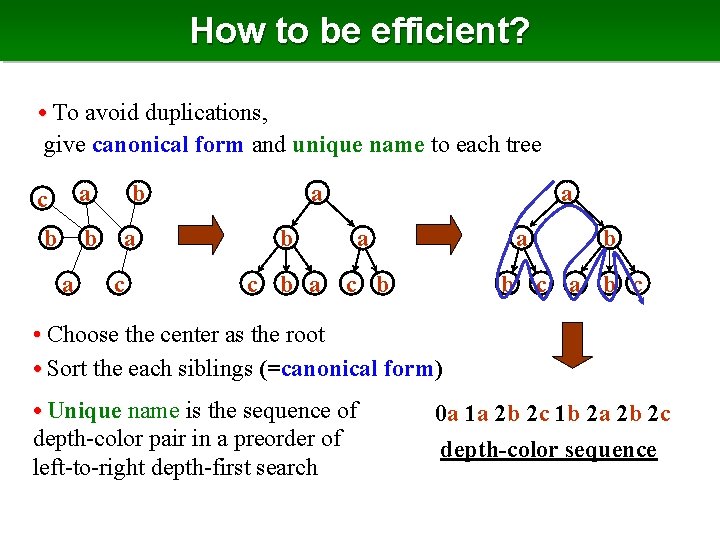
How to be efficient? • To avoid duplications, give canonical form and unique name to each tree c a b b a a b a c b a b b c a b c • Choose the center as the root • Sort the each siblings (=canonical form) • Unique name is the sequence of depth-color pair in a preorder of left-to-right depth-first search 0 a 1 a 2 b 2 c 1 b 2 a 2 b 2 c depth-color sequence

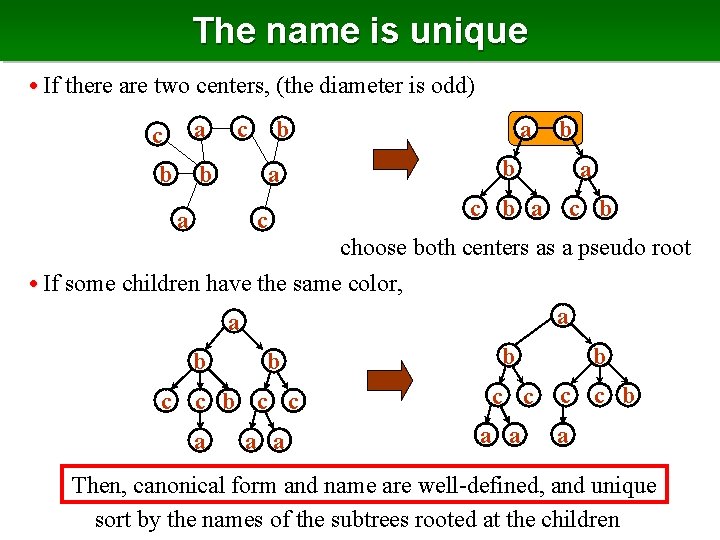
The name is unique • If there are two centers, (the diameter is odd) c a b b c b a a a c b b a c b choose both centers as a pseudo root • If some children have the same color, a a b b c c a a a b b c c b a a a Then, canonical form and name are well-defined, and unique sort by the names of the subtrees rooted at the children

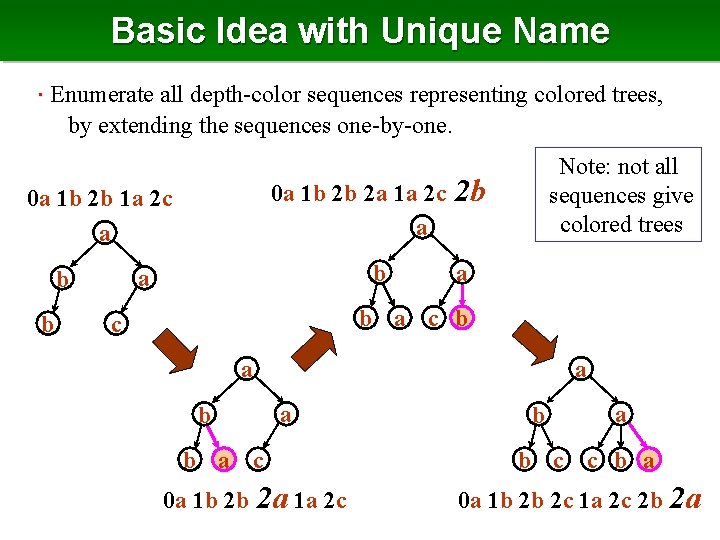
Basic Idea with Unique Name ∙ Enumerate all depth-color sequences representing colored trees, by extending the sequences one-by-one. 0 a 1 b 2 b 2 a 1 a 2 c a 0 a 1 b 2 b 1 a 2 c a b b a b Note: not all sequences give colored trees 2 b a c b c a b a c 0 a 1 b 2 b 2 a 1 a 2 c b a b c c b a 0 a 1 b 2 b 2 c 1 a 2 c 2 b 2 a

Avoid Duplication • Generate unique names, we can avoid duplications 0 a 1 b 2 b 2 a 1 a 2 c In our algorithm 1. one insertion makes a new tree 2. for each tree, insertions occur on at most two positions make each tree in constant time

Let’s See the Details • The idea of our algorithm is simple; enumerate depth-color sequences in an incremental way • But, not all depth-color sequences give colored trees • We can not generate them in a straightforward way Let’s see the details.

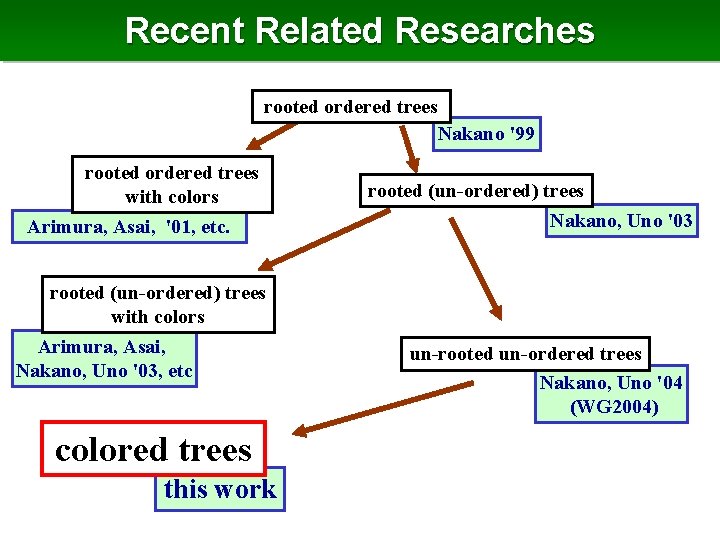
Recent Related Researches rooted ordered trees Nakano '99 rooted ordered trees with colors Arimura, Asai, '01, etc. rooted (un-ordered) trees with colors Arimura, Asai, Nakano, Uno '03, etc colored trees this work rooted (un-ordered) trees Nakano, Uno '03 un-rooted un-ordered trees Nakano, Uno '04 (WG 2004)

Enumerate Rooted Ordered Trees Nakano, Arimura, et al. • Add a vertex to be the rightmost leaf (Add a vertex at the right side of the rightmost path) Thus, we sort the children to get canonical forms, and enumerate rooted ordered trees being canonical

Enumerating Rooted (un-ordered) Trees Nakano&Uno, Arimura, et al. • Add a vertex to be a rightmost leaf so that the order changes on no siblings We set the root to the center to be canonical, and add vertices so that the center does not move

Enumeration of (Un-rooted) Trees Nakano&Uno (WG 2004) Fix diameter to 4 • Start from a path • Add vertex to be rightmost or second rightmost

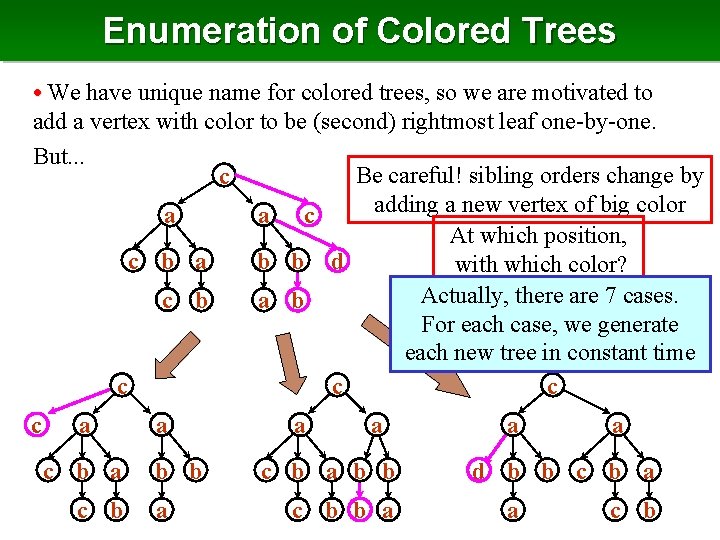
Enumeration of Colored Trees • We have unique name for colored trees, so we are motivated to add a vertex with color to be (second) rightmost leaf one-by-one. But. . . Be careful! sibling orders change by c adding a new vertex of big color a c a At which position, b b d c b a with which color? Actually, there are 7 cases. c b a b For each case, we generate each new tree in constant time c c a c b a b b a a a c b a b b c b b a a a d b b c b a a c b

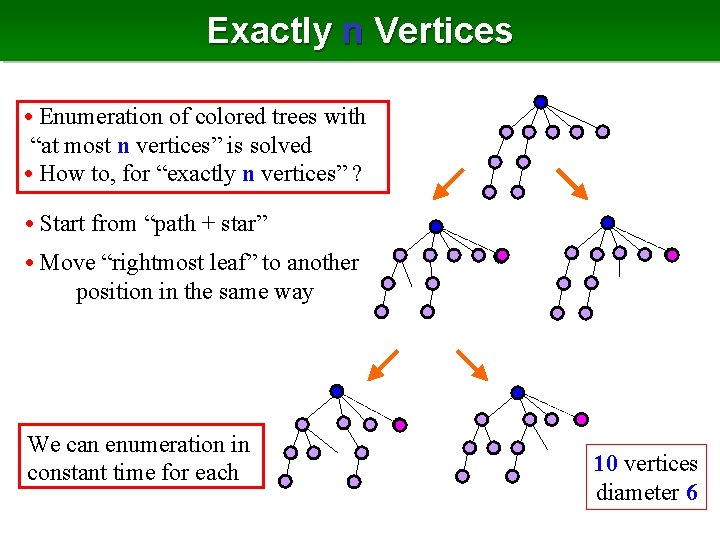
Exactly n Vertices • Enumeration of colored trees with “at most n vertices” is solved • How to, for “exactly n vertices” ? • Start from “path + star” • Move “rightmost leaf” to another position in the same way We can enumeration in constant time for each 10 vertices diameter 6

Result We propose an algorithm for the problem running in O(1) time for each, within O(n) memory In detail, time complexity: constant for each (computation time is linear in #colored trees) delay: constant space complexity: O(n)

6 -4 Floor Plans

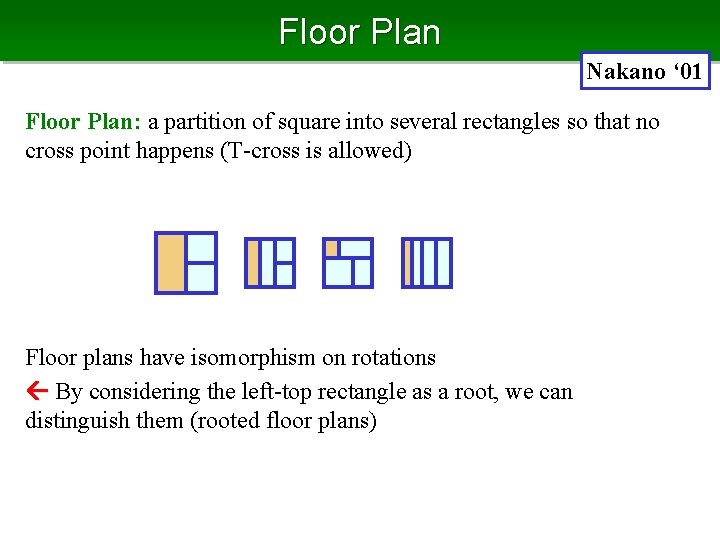
Floor Plan Nakano ‘ 01 Floor Plan: a partition of square into several rectangles so that no cross point happens (T-cross is allowed) Floor plans have isomorphism on rotations By considering the left-top rectangle as a root, we can distinguish them (rooted floor plans)

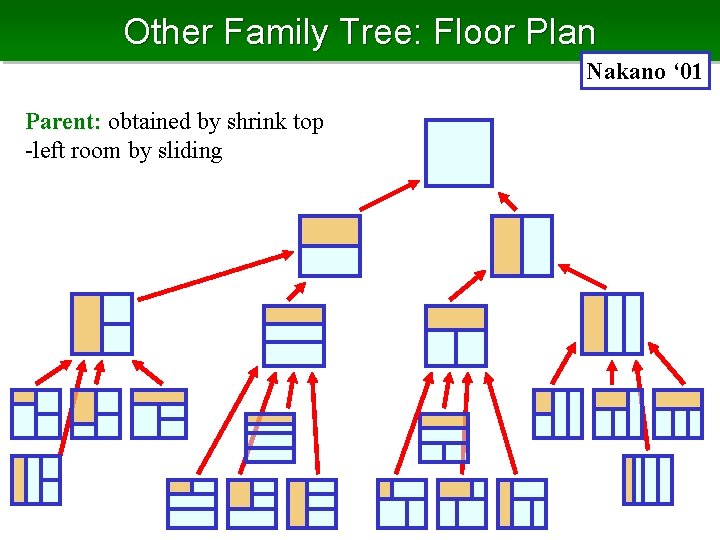
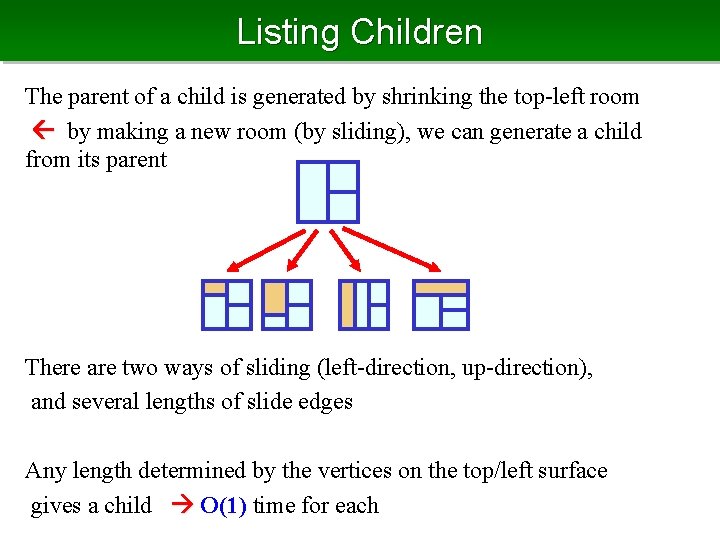
Other Family Tree: Floor Plan Nakano ‘ 01 Parent: obtained by shrink top -left room by sliding

Listing Children The parent of a child is generated by shrinking the top-left room by making a new room (by sliding), we can generate a child from its parent There are two ways of sliding (left-direction, up-direction), and several lengths of slide edges Any length determined by the vertices on the top/left surface gives a child O(1) time for each

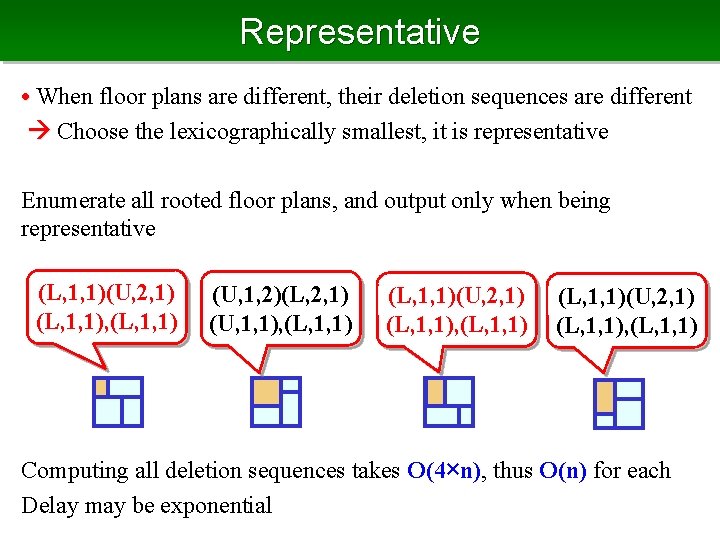
Non-rooted Floor Plan • Consider the enumeration under the isomorphism Then, we have to check the isomorphism, or use representatives To obtain parent, we delete the top-left room by sliding, and the sliding is left direction or up direction So, we can define deletion sequence for each rooted floor plan composed of (left/up, width, length)

Representative • When floor plans are different, their deletion sequences are different Choose the lexicographically smallest, it is representative Enumerate all rooted floor plans, and output only when being representative (L, 1, 1)(U, 2, 1) (L, 1, 1), (L, 1, 1) (U, 1, 2)(L, 2, 1) (U, 1, 1), (L, 1, 1)(U, 2, 1) (L, 1, 1), (L, 1, 1) Computing all deletion sequences takes O(4×n), thus O(n) for each Delay may be exponential

Other Geometric Object • In principle, any kind of geometric objects are tractable, if we define the root by an edge on the outerface, or vertex at the center, etc. For example, plane triangulations can be enumerated in output linear time

References Ordered Trees & Rooted Trees T. Asai, K. Abe, S. Kawasoe, H. Arimura, H. Sakamoto, S. Arikawa: Efficient Substructure Discovery from Large Semi-structured Data, SDM 2002: 158 -174 (2002) T. Asai, H. Arimura, T. Uno, S. Nakano, Discovering Frequent Substructures in Large Unordered Trees, DS 2003, LNAI 2843, 47 -61 (2003) S. Nakano, T. Uno, Constant Time Generation of Trees with Specified Diameter, WG 2004, LNCS 3353, 33 -45 (2004) S. Nakano, T. Uno, Generating Colored Trees, WG 2005, LNCS 3787, 249 -260 (2005) S. Nakano, T Uno, Efficient Generation of Rooted Trees, Tech. Rep. NII , 2003 Floorplans S. Nakano, Enumerating Floorplans with n Rooms, LNCS 2223, 107 -115 (2001)

Exercise

Exercise 6 -1. Check the time complexity of necklace enumeration, of each version (with/without database, representative) 6 -2. Instead of necklace, we want to enumerate all “joint of two necklaces”. Can you define some representatives and develop efficient algorithm? (two necklace are jointed at a letter) E B C A 6 -3. Can you define representative and show efficient enumeration algorithm for chain? (several necklace are joined in the same way) A D E

Exercise 6 -4. Precisely prove (or check) that the correctness of the update process of copy position 6 -5. In the necklace enumeration, we change a letter of a representative and obtain other representative. Instead of this operation, try to make an algorithm with starting from empty string, and add a letter at the last iteratively, so that the algorithm always outputs a representative at the bottom of the recursion; we have not to generate a partial string that is a prefix of no representative. Prove the correctness, and complexity

Exercise 6 -6. Precisely describe the algorithm for enumerating free trees of n vertices and odd diameter 6 -7. Make an algorithm for enumerating rooted trees such that each vertex has a label E B C D B C A A 6 -8. Can you define representative and show efficient enumeration algorithm for chain? (several necklace are joined in the same way) E

Exercise 6 -9. Describe an algorithm to enumerate all labeled rooted trees where labels are taken from alphabet Σ and put to each vertex 6 -10. Explain why labeled version is difficult for free trees but not for rooted trees 6 -11. Construct a representative for rotation trees where a rotation tree has a cyclic order on the children of each vertex (an ordering is given to children of each vertex, but rotation of the ordering is allowed) 6 -12. Construct an enumeration algorithm for rotation trees

Exercise 6 -13. Construct a floor plan s. t. all four deletion sequences obtained from rotated ones are the same (remind that no cross point (degree 4) is allowed) 6 -14. For floor plan enumeration, explain why enumeration of only representative is difficult 6 -15. Precisely describe how to enumerate all children of a floor plan in constant time for each

Exercise 6 -16. Consider an isomorphism on matrices s. t. we are allowed to rotate the rows and rotate the columns. How do you define the representatives? 6 -17. Consider whether the enumeration of only representative is possible in an efficient way or not, and if difficult, explain the reason 6 -18. Consider other isomorphism on matrices, and explain whether the representatives are hard or not, and enumeration is hard or not 6 -19. Show some geometric objects in plane whose rooted version seems to be enumerated efficiently