CSE321 Programming Languages CurryHoward Isomorphism POSTECH June 4

CSE-321 Programming Languages Curry-Howard Isomorphism 박성우 POSTECH June 4, 2006

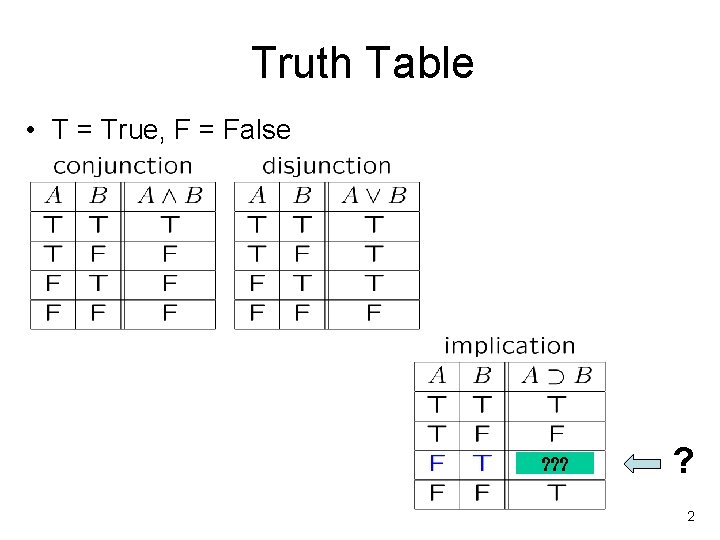
Truth Table • T = True, F = False ? ? ? ? 2

Tautology The computational meaning of ) Truth of A is not affected by truth of B. 3

Tautology But what is the computational meaning of 4

Classical Logic • Concerned with: – "whether a given proposition is true or not. " • Every proposition is either true or false. – Logic from omniscient God's point of view • Logic for mathematics • Tautologies in classical logic law of excluded middle law of double-negation Peirce's law 5

Constructive Logic • Logic from a human's point of view – we know only what we can prove. • Eg. P = NP • Logic for computer science • Not provable in constructive logic 6

Classical vs. Constructive • Proposition: there exists a rational number ab such that a and b are both irrational numbers. • Proof in classical logic – let c = p 2 p 2 • if c = p 2 p 2 is rational, let a = b = p 2 = irrational. then ab = p 2 p 2 = rational. • if c = p 2 p 2 is irrational, let a = c = p 2 p 2 = irrational, b = p 2 = irrational. then ab = (p 2 p 2)p 2 = p 22 = rational. – But what are a and b at all? • Proof in constructive logic – more involved, but provides a and b. 7

Constructive Conjunction 8

Constructive Implication 9

Disjunction ? 10

Outline • Classical logic vs Constructive logic V • Curry-Howard isomorphism • Summary 11

Curry-Howard Isomorphism Logic Type System proposition type proof term (expression) 12

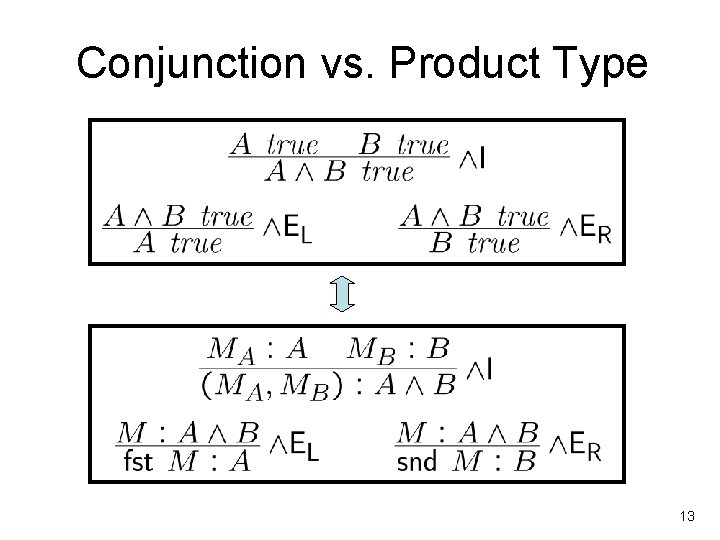
Conjunction vs. Product Type 13

Logic vs. Type System 14

-Reduction 15

-Reduction 16

Curry-Howard Isomorphism Logic Type System propositional logic simply-type -calculus first-order logic dependent types second-order logic polymorphism modal logic modal type system classical logic continuations ? 17

Four Color Problem • "Every map can be colored with no more than 4 colors. " 5 4 • Proposed in 1852 ! 7 0 0 2 • Computer-based solution published in 1976 LICS Fall in t h g • Formalization of the proof in 1994 tau e b to – theorem prover Coq 18

Outline • Classical logic vs Constructive logic V • Curry-Howard isomorphism V • Summary 19

Curry 20

Howard 21

Curry-Howard Isomorphism = 22

Finally we will have. . .

Final Exam • 3 hours • Closed book • Covers all chapters. Su Mo Tu We Th Fr 1 3 4 5 6 7 8 10 11 12 13 14 15 17 18 19 20 21 22 24 25 26 27 28 29 Sa 2 9 16 23 30 24