Graph Isomorphism Algorithms and networks Today Graph isomorphism

Graph Isomorphism Algorithms and networks

Today • • Graph isomorphism: definition Complexity: isomorphism completeness The refinement heuristic Isomorphism for trees – Rooted trees – Unrooted trees Graph Isomorphism 2

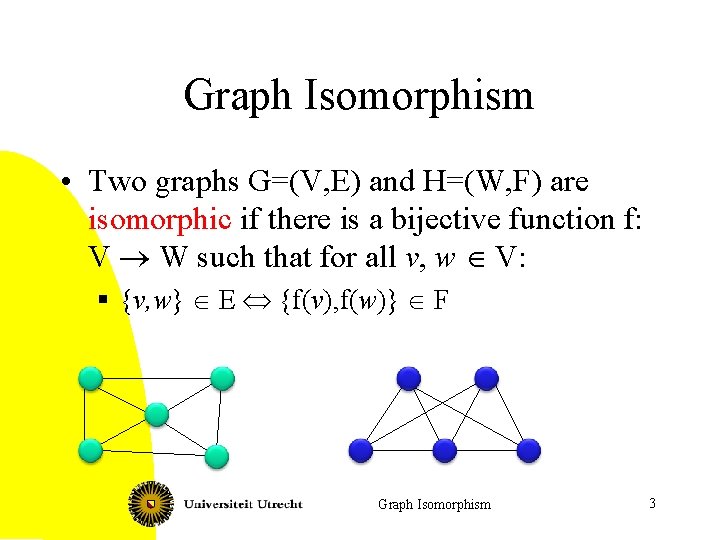
Graph Isomorphism • Two graphs G=(V, E) and H=(W, F) are isomorphic if there is a bijective function f: V ® W such that for all v, w Î V: § {v, w} Î E Û {f(v), f(w)} Î F Graph Isomorphism 3

Applications • Chemistry: databases of molecules (etc. ) – Actually needed: canonical form of molecule structure / graph • Design verification • Software plagiarism detection • Speeding up algorithms for highly symmetric graphs Graph Isomorphism 4

Variant for labeled graphs • Let G = (V, E), H=(W, F) be graphs with vertex labelings l: V ® L, l’ ® L. • G and H are isomorphic labeled graphs, if there is a bijective function f: V ® W such that – For all v, w Î V: {v, w} Î E Û {f(v), f(w)} Î F – For all v Î V: l(v) = l’(f(v)). • Application: organic chemistry: – determining if two molecules are identical. Graph Isomorphism 5

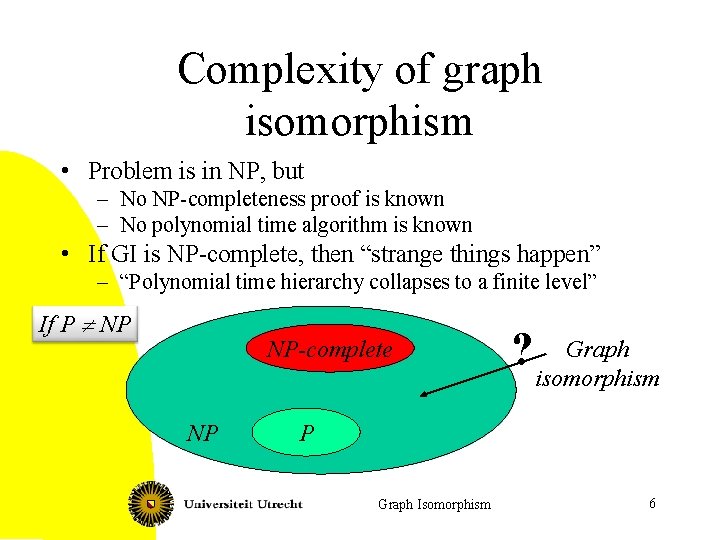
Complexity of graph isomorphism • Problem is in NP, but – No NP-completeness proof is known – No polynomial time algorithm is known • If GI is NP-complete, then “strange things happen” – “Polynomial time hierarchy collapses to a finite level” If P ¹ NP NP-complete NP Graph ? isomorphism P Graph Isomorphism 6

Isomorphism-complete • Problems are isomorphismcomplete, if they are `equally hard’ as graph isomorphism – Isomorphism of bipartite graphs – Isomorphism of labeled graphs – Automorphism of graphs • Given: a graph G=(V, E) • Question: is there a non-trivial automorphism Graph Isomorphism 7

Automorphism • An automorphism is a bijective function f: V ® V with for all v, wÎV: § {v, w} Î E, if and only if {f(v), f(w)} Î E. § A non-trivial automorphism is an automorphism that is not the identity § G 1 has 6 automorphisms, and 5 nontrivial automorphisms § G 2 has 2 automorphisms, and 1 nontrivial automorphism Graph Isomorphism G 1 w v G 2 8

More isomorphism complete problems • • • Finding a graph isomorphism f Isomorphism of semi-groups Isomorphism of finite automata Isomorphism of finite algebra’s Isomorphism of – – – Connected graphs Directed graphs Regular graphs Perfect graphs Chordal graphs Graphs that are isomorphic with their complement Graph Isomorphism 9

Special cases are easier • Polynomial time algorithms for – Graphs of bounded degree – Planar graphs This course – Trees – Bounded treewidth • Expected polynomial time for random graphs Graph Isomorphism 10

An equivalence relation on vertices • Say v ~ w, if and only if there is an automorphism mapping v to w. • ~ is an equivalence relation • Partitions the vertices in automorphism classes • Tells on structure of graph Graph Isomorphism 11

Iterative vertex partition heuristic: the idea • Partition the vertices of G and H in classes • Each class for G has a corresponding class for H. • Property: vertices in class must be mapped to vertices in corresponding class • Refine classes as long as possible • When no refinement possible, check all possible ways that `remain’. Graph Isomorphism 12

Iterative vertex partition heuristic skeleton • Partition the vertices of G and H in classes – If v and w are in different classes, there is no isomorphism or automorphism mapping v to w • Repeat – Refine the classes Until … we do not find refinements • Solve Graph Isomorphism 13

Iterative vertex partition heuristic • If |V| ¹ |W|, or |E| ¹ |F|, output: no. Done. • Otherwise, we partition the vertices of G and H into classes, such that – Each class for G has a corresponding class for H – If f is an isomorphism from G to H, then f(v) belongs to the class, corresponding to the class of v. • First try: vertices belong to the same class, when they have the same degree. – If f is an isomorphism, then the degree of f(v) equals the degree of v for each vertex v. Graph Isomorphism 14

Scheme • Start with sequence SG = (A 1) of subsets of G with A 1=V, and sequence SH = (B 1) of subsets of H with B 1=W. • Repeat until … – Replace Ai in SG by Ai 1, …, Air and replace Bi in SH by Bi 1, …, Bir. • Ai 1, …, Air is partition of Ai • Bi 1, …, Bir is partition of Bi • For each isormorphism f: v in Aij if and only if f(v) in Bij Graph Isomorphism 15

Possible refinement • Count for each vertex in Ai and Bi how many neighbors they have in Aj and Bj for some i, j. • Set Ais = {v in Ai | v has s neighbors in Aj}. • Set Bis = {v in Bi | v has s neighbors in Bj}. • Invariant: for all v in the ith set in SG, f(v) in the ith set in SH. • If some |Ai| ¹ |Bi|, then stop: no isomorphism. Graph Isomorphism 16

Other refinements • Partition upon other characteristics of vertices – Label – Number of vertices at distance d (in a set Ai). –… Graph Isomorphism 17

After refining • If each Ai contains one vertex: check the only possible isomorphism. • Otherwise, cleverly enumerate all functions that are still possible, and check these. • Works well in practice! Graph Isomorphism 18

Isomorphism on trees • Linear time algorithm to test if two (labeled) trees are isomorphic. (Aho, Hopcroft, Ullman, 1974) • Algorithm to test if two rooted trees are isomorphic. • Used as a subroutine for unrooted trees. Graph Isomorphism 19

Rooted tree isomorphism • For a vertex v in T, let T(v) be the subtree of T with v as root. • Level of vertex: distance to root. • If T 1 and T 2 have different number of levels: not isomorphic, and we stop. Otherwise, we continue: Graph Isomorphism 20

Structure of algorithm • Tree is processed level by level, from bottom to root • Processing a level: – A long label for each vertex is computed – This is transformed to a short label • Vertices in the same layer whose subtrees are isomorphic get the same labels: – If v and w on the same level, then • L(v)=L(w), if and only if T(v) and T(w) are isomorphic with an isomorphism that maps v to w. Graph Isomorphism 21

Labeling procedure • For each vertex, get the set of labels assigned to its children. • Sort these sets. – Bucketsort the pairs (L(w), v) for T 1, w child of v – Bucketsort the pairs (L(w), v) for T 2, w child of v • For each v, we now have a long label LL(v) which is the sorted set of labels of the children. • Use bucketsort to sort the vertices in T 1 and T 2 such that vertices with same long label are consecutive in ordering. Graph Isomorphism 22

On sorting w. r. t. the long lists (1) • Preliminary work: – Sort the nodes is the layer on the number of children they have. • Linear time. (Counting sort / Radix sort. ) – Make a set of pairs (j, i) with (j, i) in the set when the jth number in a long list is i. – Radix sort this set of pairs. Graph Isomorphism 23

On sorting w. r. t. the long lists (2) • Let q be the maximum length of a long list • Repeat – Distribute among buckets the nodes with at least q children, with respect to the qth label in their long list • Nodes distributed in buckets in earlier round are taken here in the order as they appear in these buckets. • The sorted list of pairs (j, i) is used to skip empty buckets in this step. – q --; – Until q=0. Graph Isomorphism 24

After vertices are sorted with respect to long label • Give vertices with same long label same short label (start counting at 0), and repeat at next level. • If we see that the set of labels for a level of T 1 is not equal to the set for the same level of T 2, stop: not isomorphic. Graph Isomorphism 25

Time • One layer with n 1 nodes with n 2 nodes in next layer costs O(n 1 + n 2) time. • Total time: O(n). Graph Isomorphism 26

Unrooted trees • Center of a tree – A vertex v with the property that the maximum distance to any other vertex in T is as small as possible. – Each tree has a center of one or two vertices. • Finding the center: – Repeat until we have a vertex or a single edge: • Remove all leaves from T. – O(n) time: each vertex maintains current degree in variable. Variables are updated when vertices are removed, and vertices put in set of leaves when their degree becomes 1. Graph Isomorphism 27

Isomorphism of unrooted trees • Note: the center must be mapped to the center • If T 1 and T 2 both have a center of size 1: – Use those vertices as root. • If T 1 and T 2 both have a center of size 2: – Try the two different ways of mapping the centers – Or: subdivide the edge between the two centers and take the new vertices as root • Otherwise: not isomorphic. • 1 or 2 calls to isomorphism of rooted trees: O(n). Graph Isomorphism 28

Conclusions • Similar methods work for finding automorphisms • We saw: heuristic for arbitrary graphs, algorithm for trees • There algorithms for several special graph classes (e. g. , planar graphs, graphs of bounded degree, …) • The related Subgraph Isomorphism problem is NP-complete Graph Isomorphism 29