Garys Work on Graph Isomorphism 1 1 6

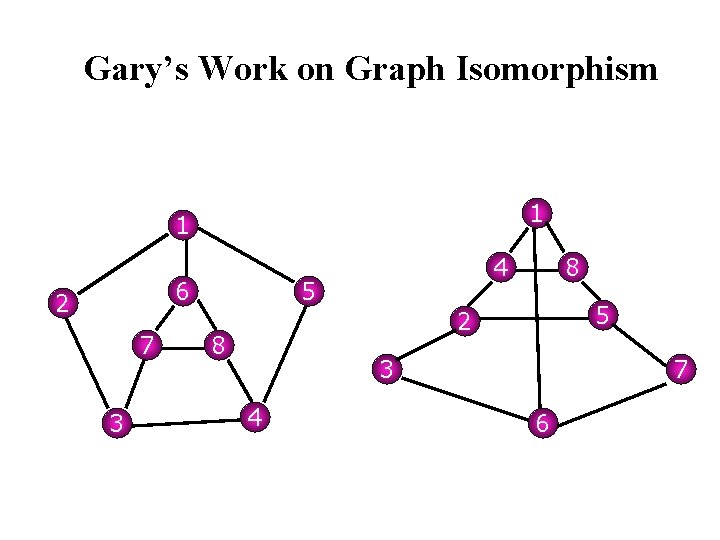
Gary’s Work on Graph Isomorphism 1 1 6 2 7 3 4 5 8 5 2 8 3 4 7 6

Gary’s Papers on Graph Isomorphism On the n log n isomorphism technique: a preliminary report. ACM STOC, 1978. Isomorphism testing for graphs of bounded genus. ACM STOC, 1980 Isomorphism of graphs which are pairwise k-separable. Information & Control, 1983. Isomorphism of k-contractible graphs: a generalization of bounded valence and bounded genus. Information & Control, 1983.

Gary’s Papers on Graph Isomorphism

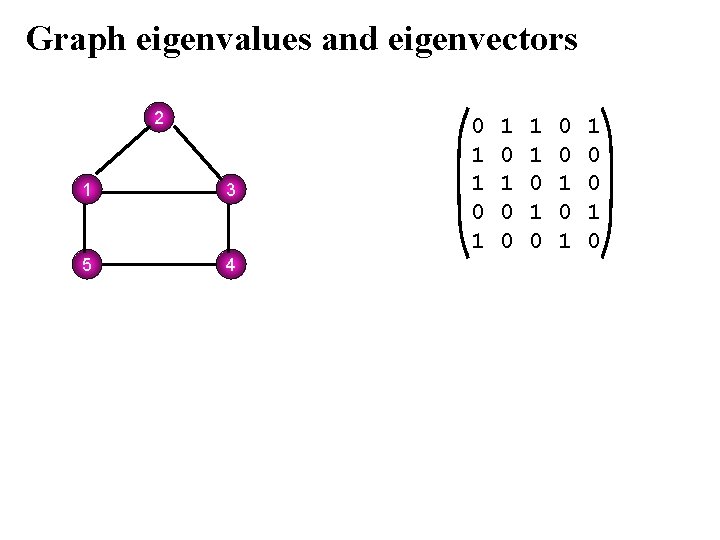
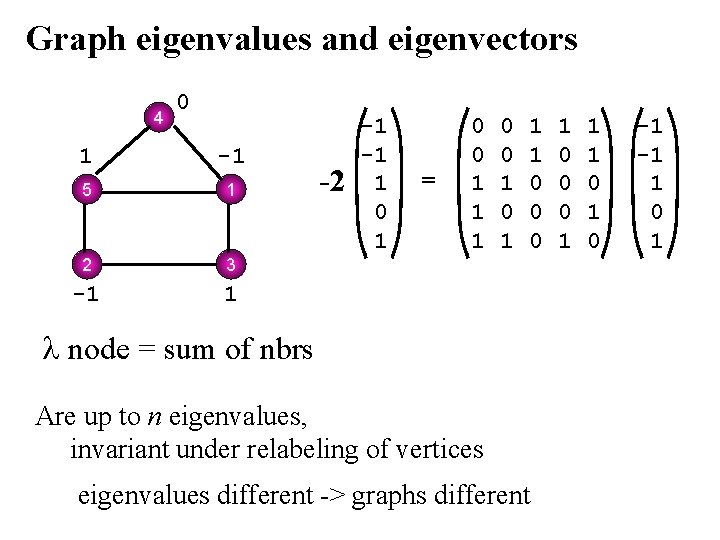
Graph eigenvalues and eigenvectors 2 1 3 5 4 0 1 1 0 1 0 0 1 1 0 0 1 0

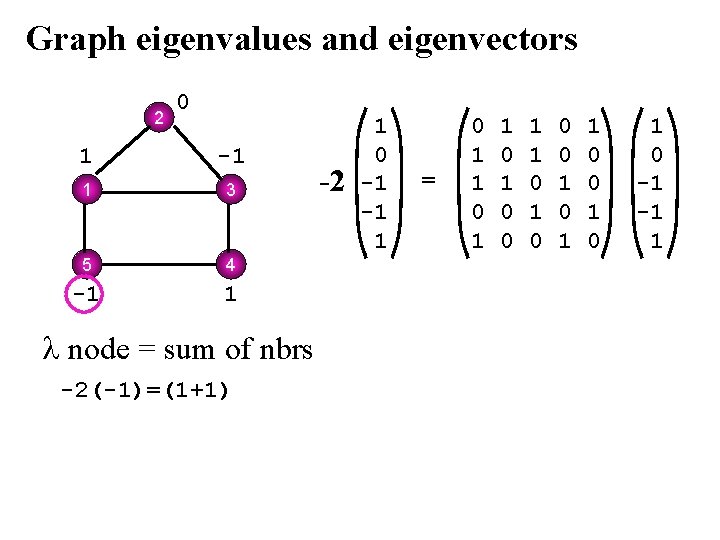
Graph eigenvalues and eigenvectors 2 0 1 -1 1 3 5 4 -1 1 node = sum of nbrs -2(-1)=(1+1) -2 1 0 -1 -1 1 = 0 1 1 0 1 0 0 1 1 0 0 1 0 -1 -1 1

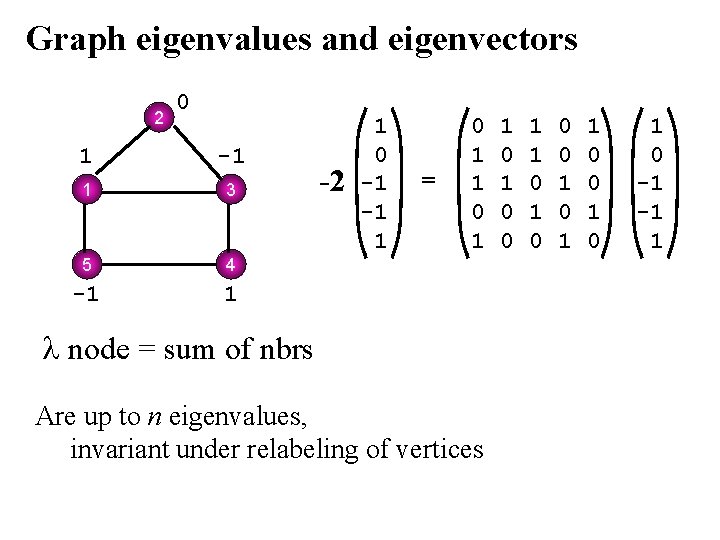
Graph eigenvalues and eigenvectors 2 0 1 -1 1 3 5 4 -1 1 -2 1 0 -1 -1 1 = 0 1 1 0 1 node = sum of nbrs Are up to n eigenvalues, invariant under relabeling of vertices 1 0 0 1 1 0 0 1 0 -1 -1 1

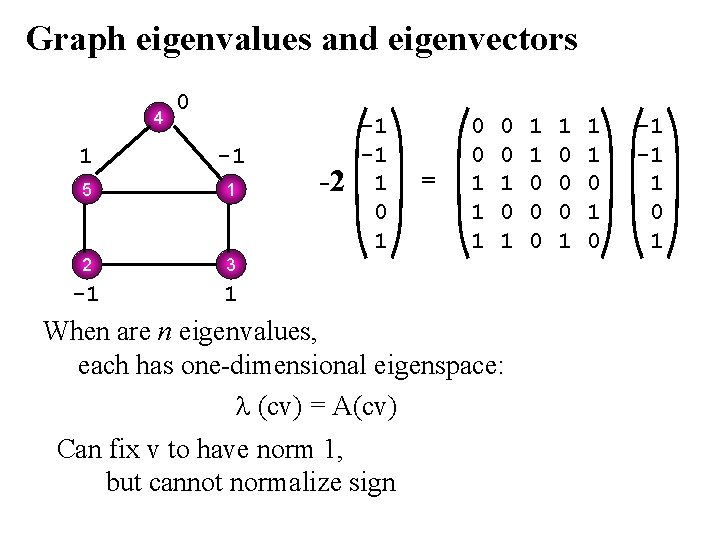
Graph eigenvalues and eigenvectors 4 0 1 -1 5 1 2 3 -1 1 -2 -1 -1 1 0 1 = 0 0 1 1 1 0 0 0 node = sum of nbrs Are up to n eigenvalues, invariant under relabeling of vertices eigenvalues different -> graphs different 1 0 0 0 1 1 1 0 -1 -1 1 0 1

Graph eigenvalues and eigenvectors 4 0 1 -1 5 1 2 3 -1 1 -2 -1 -1 1 0 1 = 0 0 1 1 1 0 0 1 When are n eigenvalues, each has one-dimensional eigenspace: (cv) = A(cv) Can fix v to have norm 1, but cannot normalize sign 1 1 0 0 0 1 1 1 0 -1 -1 1 0 1

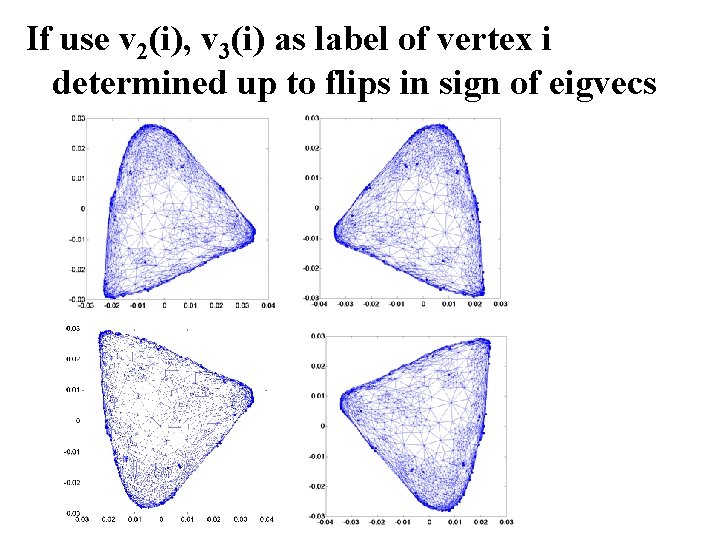
Testing isomorphism when G and H have same eigenvalues Compute eigenvectors of G: v 1, v 2, …, vn and eigenvectors of H: u 1, u 2, …, un Goal: Label vertex i by v 1(i), v 2(i), …, vn(i) But, eigenvectors only determined up to sign.

A Delaunayed Gary

Embedding of graph using two eigvecs v 3(i) v 2(i)

If use v 2(i), v 3(i) as label of vertex i determined up to flips in sign of eigvecs

Testing isomorphism when G and H have same eigenvalues Isomorphic iff are signs s. t. set of labels are same. v 1: . 50 v 2: -. 43 v 3: . 50 v 4: . 18 v 5: . 53 § u 1: § u 2: § u 3: § u 4: § u 5: 0 -. 50. 74 -. 43. 12 0 -. 50. 52. 18 -. 58. 43. 53. 36 -. 50 -. 12. 50 -. 58. 36 . 50 -. 50 0. 43 -. 74. 50 -. 50 0. 18. 52. 53. 43 l 1 = -2. 0000 l 2 = -1. 1701 l 3 = 0. 0000 l 4 = 0. 6889 l 5 = 2. 4812 label of node 2

Distinguish verts when labels allow. Make signs cannonical when possible. v 1: . 50 v 2: -. 43 v 3: . 50 v 4: . 18 v 5: . 53 0 -. 50. 74 -. 43. 12 0 -. 50. 52. 18 -. 58. 43. 53. 36 Can only map to each other § u 1: § u 2: § u 3: § u 4: § u 5: -. 50 -. 12. 50 -. 58. 36 . 50 -. 50 0. 43 -. 74. 50 -. 50 0. 18. 52. 53. 43

Distinguish verts when labels allow. Make signs canonical when possible. v 1: . 50 v 2: -. 43 v 3: . 50 v 4: . 18 v 5: . 53 0 -. 50. 74 -. 43. 12 0 -. 50. 52. 18 -. 58. 43. 53. 36 Can only map to each other Fix signs so that labels are same § u 1: § u 2: § u 3: § u 4: § u 5: -. 50 -. 12. 50 -. 58. 36 . 50 -. 50 0. 43 -. 74. 50 -. 50 0. 18. 52. 53. 43

Distinguish verts when labels allow. Make signs canonical when possible. v 1: . 50 v 2: -. 43 v 3: . 50 v 4: . 18 v 5: . 53 0 -. 50. 74 -. 43. 12 0 -. 50. 52. 18 -. 58. 43. 53. 36 Can only map to each other Fix signs so that labels are same § u 1: § u 2: § u 3: § u 4: § u 5: -. 50. 50 -. 50. 12 -. 43. 50 -. 58. 18. 36. 53 0. 74 0. 52. 43

More formally, Partition vertices into classes, initially by |vk(i)| If some class has more positive than negative entries in a vk, make sign canonical. (2, -2, 1, 1, 1, -1, -1) Partition vertices into classes by vk(i), for vk with canonical signs.

More formally, Partition vertices into classes, initially by |vk(i)| If some class has more positive than negative entries in a vk, make sign canonical. (2, -2, 1, 1, 1, -1, -1) Partition vertices into classes by vk(i), for vk with canonical signs. Do same for all products vk 1(i)*vk 2(i)*. . . *vkr(i)

For all products? Either vk (i)*. . . *vk (i) 1 2 r splits class: v 1: 1 1 -1 -1 v 2: 1 1 -1 -1 1 1 v 3: 1 -1 1 1 -1 -1 v 3: 1 -1 -1 or vkr = product of some of vk 1*vk 2*. . . *vkr-1 on that class. v 1: 1 v 2: 1 v 4: 1 1 -1 -1 1 1 1 -1 -1 v 4 = v 1 v 2

When finished All classes have form v 1: 1 v 2: 1 v 4: 1 1 -1 -1 1 1 1 -1 -1 v 4 = v 1 v 2 Can solve for all automorphisms of G, and all isomorphisms of G and H by linear eqns over GF(2)

What about high eigenvalue multiplicity? Worst case: Strongly regular graphs Are two general families: Latin Square graphs and Steiner Triple Systems On the n log n isomorphism technique: a preliminary report. ACM STOC, 1978.