Discrete Mathematics Chapter8 Graphs 8 1 Introduction to




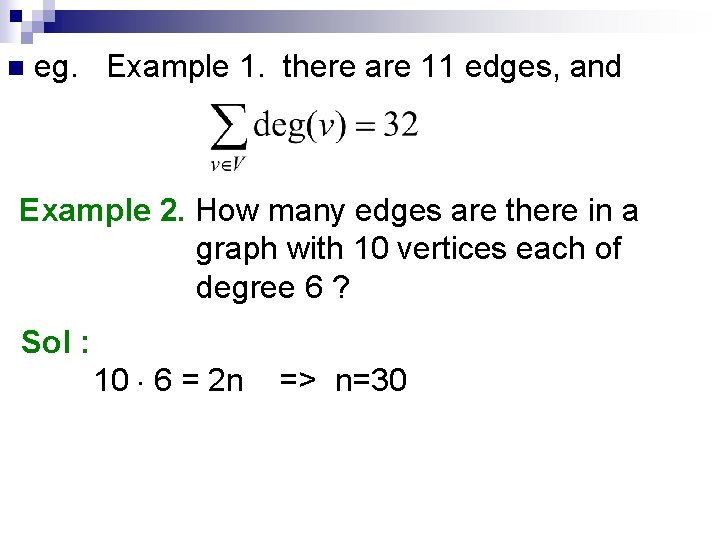





















- Slides: 49

Discrete Mathematics Chapter-8 Graphs

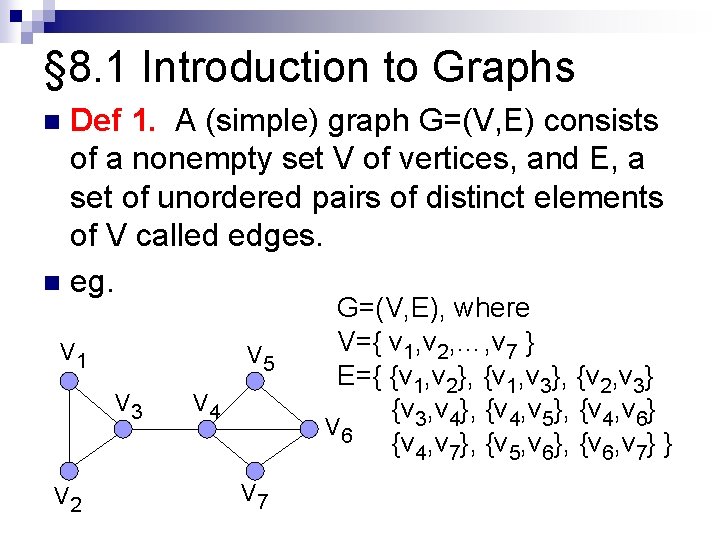
§ 8. 1 Introduction to Graphs Def 1. A (simple) graph G=(V, E) consists of a nonempty set V of vertices, and E, a set of unordered pairs of distinct elements of V called edges. n eg. n V 1 V 5 V 3 V 2 V 4 V 7 G=(V, E), where V={ v 1, v 2, …, v 7 } E={ {v 1, v 2}, {v 1, v 3}, {v 2, v 3} {v 3, v 4}, {v 4, v 5}, {v 4, v 6} V 6 {v 4, v 7}, {v 5, v 6}, {v 6, v 7} }

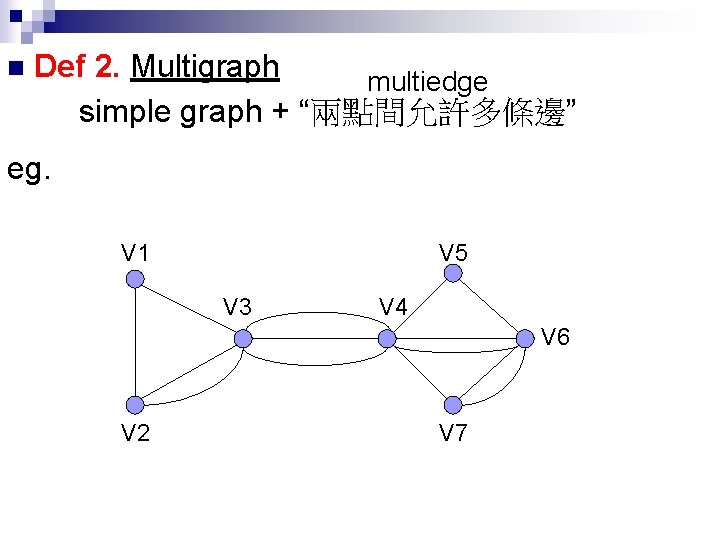
n Def 2. Multigraph multiedge simple graph + “兩點間允許多條邊” eg. V 1 V 5 V 3 V 4 V 6 V 2 V 7

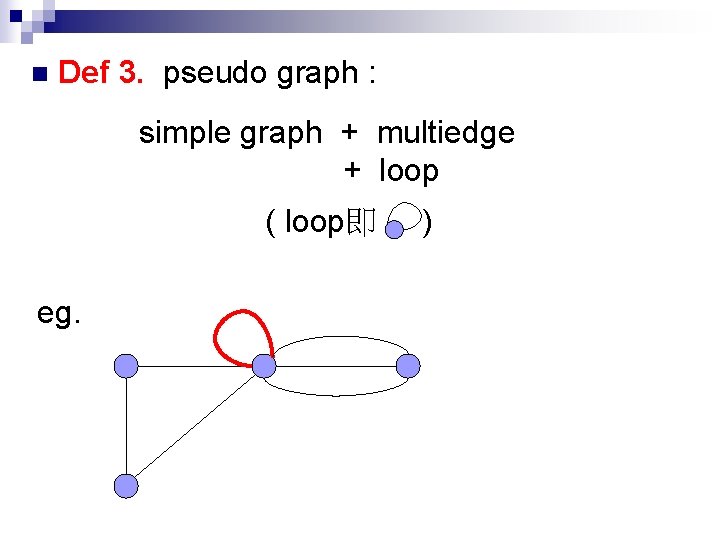
n Def 3. pseudo graph : simple graph + multiedge + loop ( loop即 eg. )

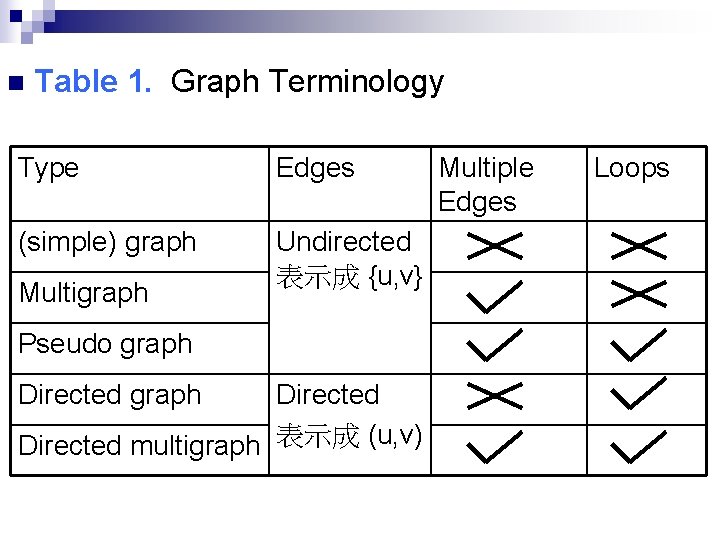
n Table 1. Graph Terminology Type Edges (simple) graph Undirected 表示成 {u, v} Multigraph Pseudo graph Directed multigraph 表示成 (u, v) Multiple Edges Loops

n Note: directed multigraph 中 U V 是 multiedge 邊為(u, v), (u, v) Exercise : 3, 5, 6, 7, 9 U V 不是 multiedge 邊為(u, v), (v, u)

§ 8. 2 Graph Terminology (undirected) n Def 1. Two vertices u and v in a graph G are called adjacent in G if {u, v} is an edge of G. (Note : 點跟點相連 : adjacent 點跟邊相連 : incident ) n Def 2. The degree of a vertex v, denoted by deg(v), in an (undirected) graph is the number of edges incident with it. (Note : loop要算 2次)

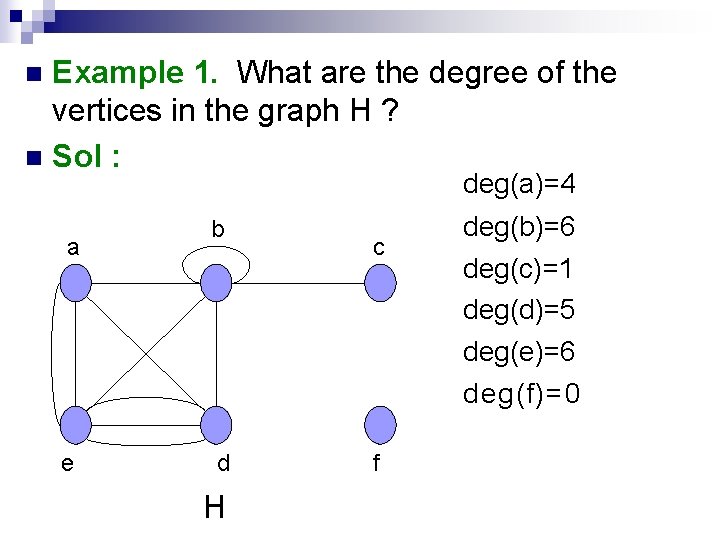
Example 1. What are the degree of the vertices in the graph H ? n Sol : n deg(a)=4 a e b d H c f deg(b)=6 deg(c)=1 deg(d)=5 deg(e)=6 deg(f)=0

n Def. A vertex of degree 0 is called isolated. eg. “ f ” in Example 1. Thm 1. (The Handshaking Theorem) Let G=(V, E) be an undirected graph with n edges (i. e. , |E|=n). Then Pf : 每條edge {u, v}會貢獻一個degree給u跟v
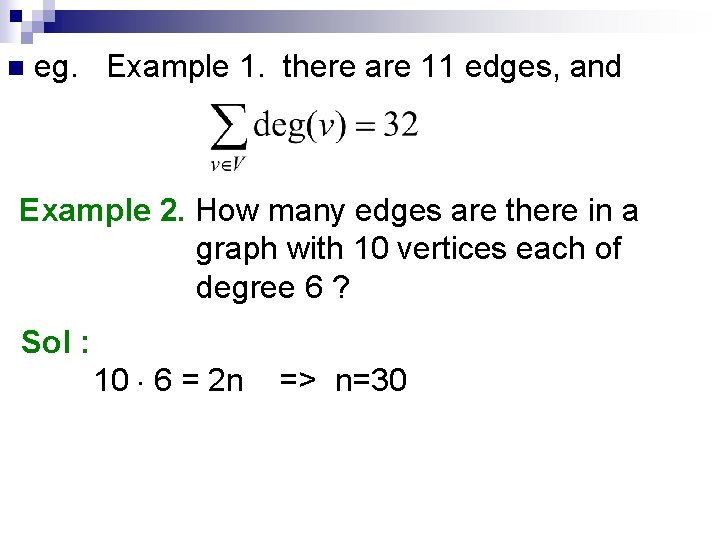
n eg. Example 1. there are 11 edges, and Example 2. How many edges are there in a graph with 10 vertices each of degree 6 ? Sol : 10 6 = 2 n => n=30

n Thm 2. An undirected graph has an even number of vertices of odd degree. n Def 3. G: directed graph , G=(V, E) (u, v) E : u is adjacent to v v is adjacent from u u : initial vertex , v : terminal vertex u v

n Def 4. G=(V, E) : directed graph v V deg(v) : # of edges with v as a terminal. (in-degree) deg+(v) : # of edges with v as a initial vertex

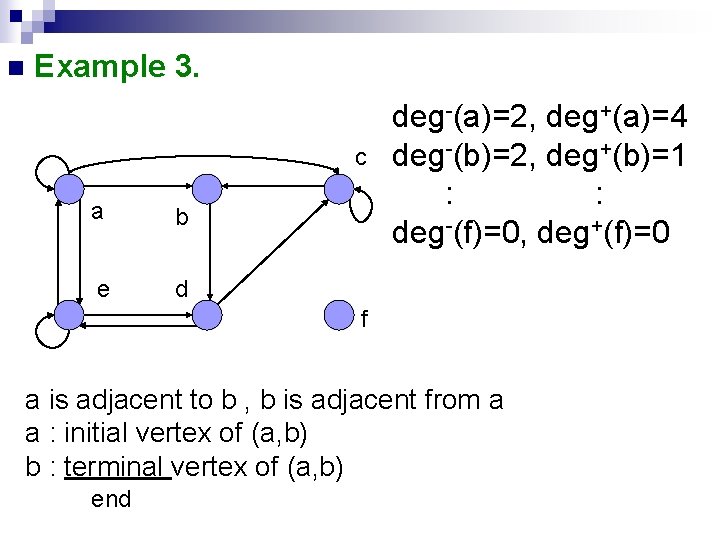
n Example 3. c a b e d deg-(a)=2, deg+(a)=4 deg-(b)=2, deg+(b)=1 : : deg-(f)=0, deg+(f)=0 f a is adjacent to b , b is adjacent from a a : initial vertex of (a, b) b : terminal vertex of (a, b) end

n Thm 3. Let G=(V, E) be a digraph. Then pf : 每個 a b edge貢獻一個 out–degree 給 a 一個 in–degree 給 b

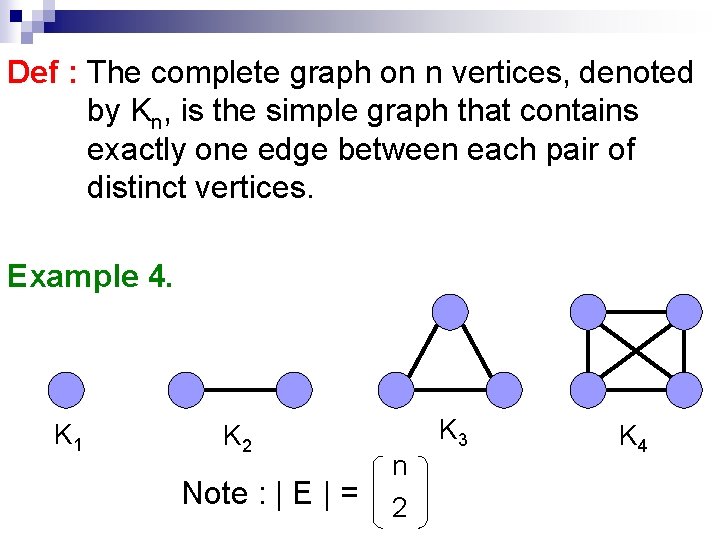
Def : The complete graph on n vertices, denoted by Kn, is the simple graph that contains exactly one edge between each pair of distinct vertices. Example 4. K 1 K 2 Note : | E | = n 2 K 3 K 4

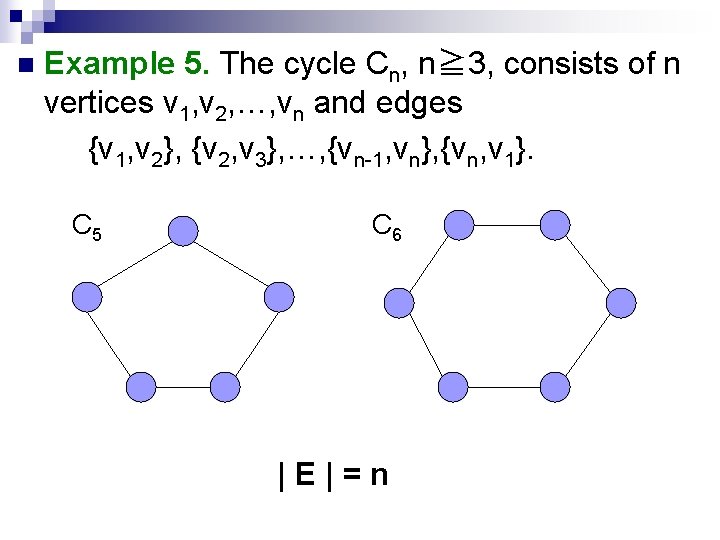
n Example 5. The cycle Cn, n≧ 3, consists of n vertices v 1, v 2, …, vn and edges {v 1, v 2}, {v 2, v 3}, …, {vn-1, vn}, {vn, v 1}. C 5 C 6 |E|=n

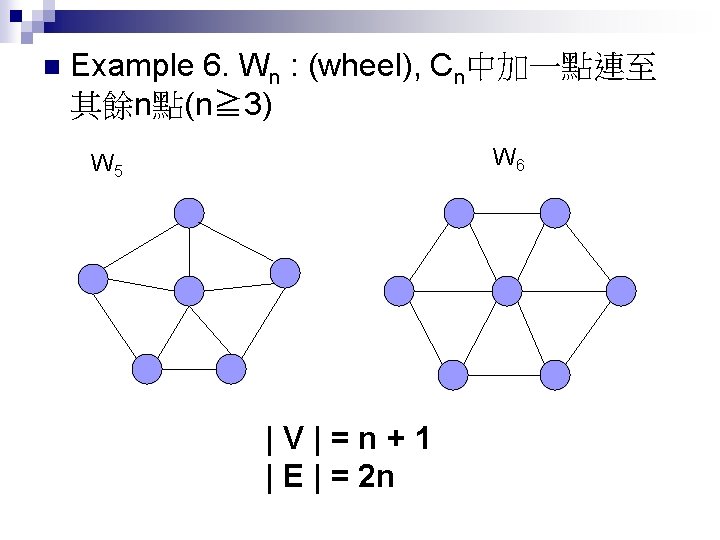
n Example 6. Wn : (wheel), Cn中加一點連至 其餘n點(n≧ 3) W 6 W 5 |V|=n+1 | E | = 2 n

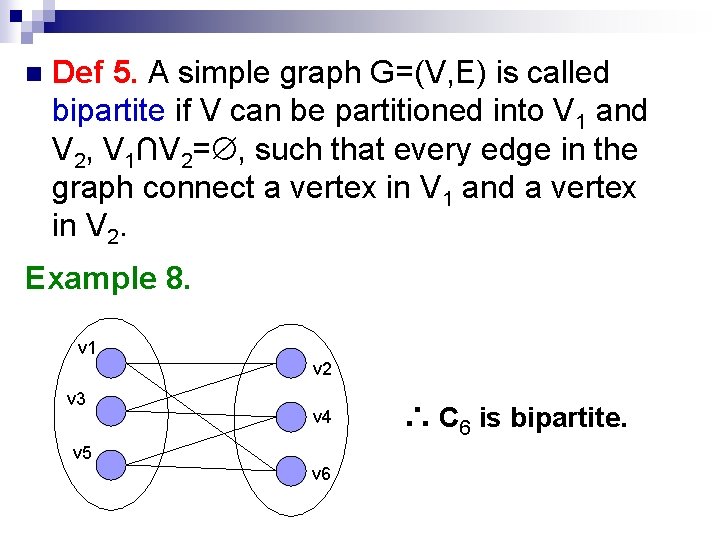
n Def 5. A simple graph G=(V, E) is called bipartite if V can be partitioned into V 1 and V 2, V 1∩V 2= , such that every edge in the graph connect a vertex in V 1 and a vertex in V 2. Example 8. v 1 v 2 v 3 v 4 v 5 v 6 ∴ C 6 is bipartite.

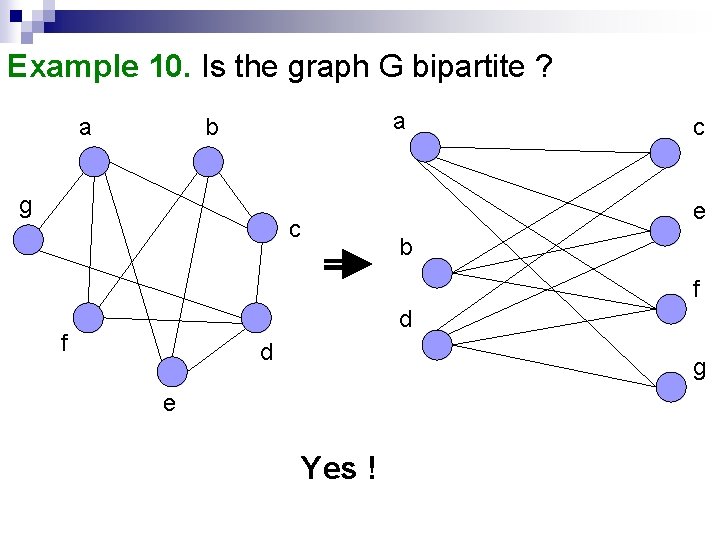
Example 10. Is the graph G bipartite ? a a b g c e c b f d g e Yes !

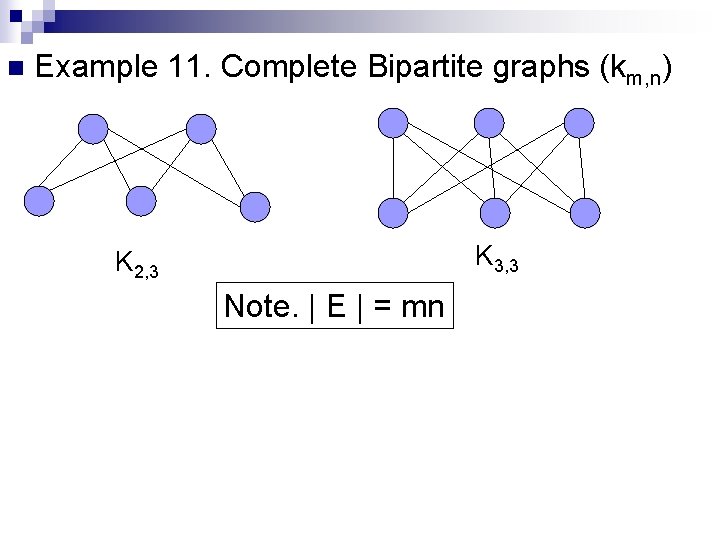
n Example 11. Complete Bipartite graphs (km, n) K 3, 3 K 2, 3 Note. | E | = mn

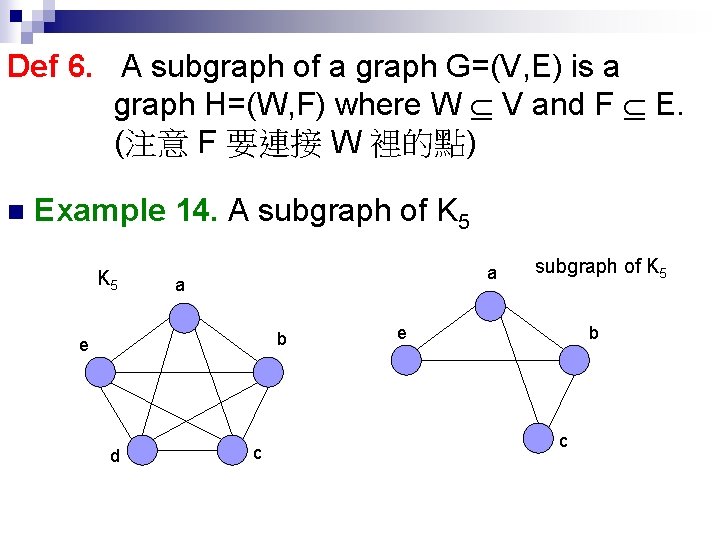
Def 6. A subgraph of a graph G=(V, E) is a graph H=(W, F) where W V and F E. (注意 F 要連接 W 裡的點) n Example 14. A subgraph of K 5 a a b e d c subgraph of K 5 e b c

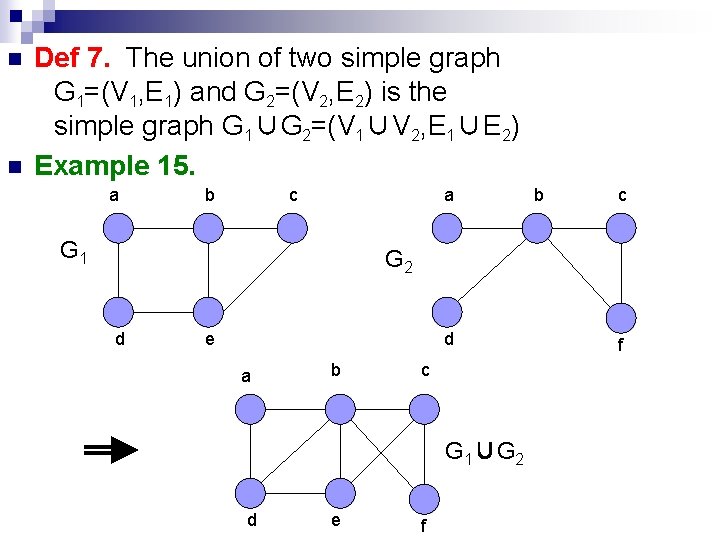
n n Def 7. The union of two simple graph G 1=(V 1, E 1) and G 2=(V 2, E 2) is the simple graph G 1∪G 2=(V 1∪V 2, E 1∪E 2) Example 15. a b c a G 1 b c G 2 d e d a b c G 1∪G 2 d e f f

ex 35上面 A simple graph G=(V, E) is called regular if every vertex of this graph has the same degree. A regular graph is called n-regular if deg(v)=n , v V. eg. K 4 : Exercise : 5, 7, 21, 23, 25, 37 is 3 -regular.

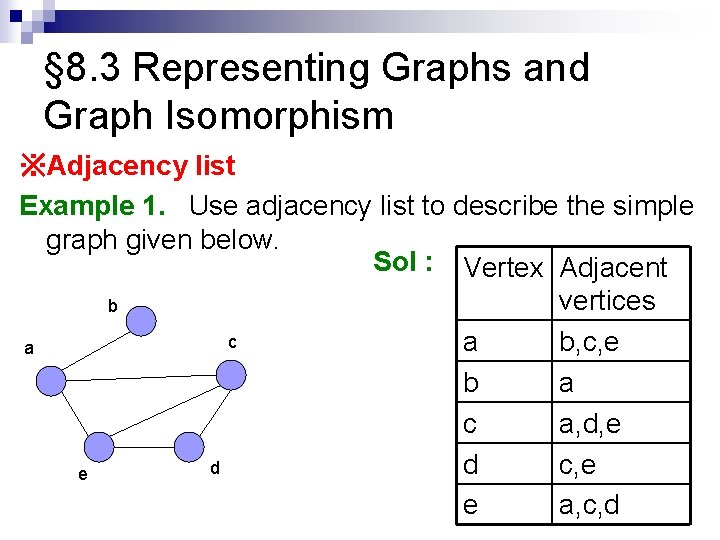
§ 8. 3 Representing Graphs and Graph Isomorphism ※Adjacency list Example 1. Use adjacency list to describe the simple graph given below. Sol : Vertex Adjacent vertices b c a b, c, e a b a c a, d, e d c, e d e e a, c, d

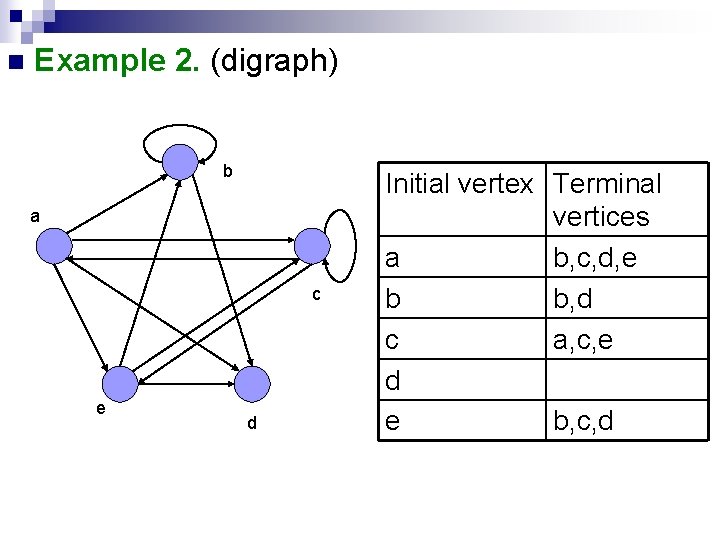
n Example 2. (digraph) b a c e d Initial vertex Terminal vertices a b, c, d, e b b, d c a, c, e d e b, c, d

※Adjacency Matrices Def. G=(V, E) : simple graph, a b c d a V={v 1, v 2, …, vn}. (順序沒關系) Example 3. b A matrix A is called the adjacency matrix of c G if A=[a a b ij]nxn , where undirected d b b c d d c a graph 的連 通矩陣必 “對稱”

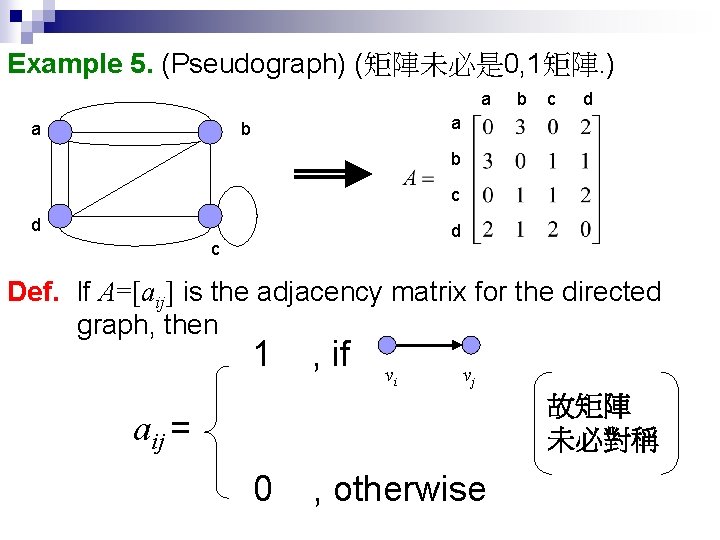
Example 5. (Pseudograph) (矩陣未必是 0, 1矩陣. ) a a b c d a b b c d d c Def. If A=[aij] is the adjacency matrix for the directed graph, then 1 , if vi vj 故矩陣 未必對稱 aij = 0 , otherwise

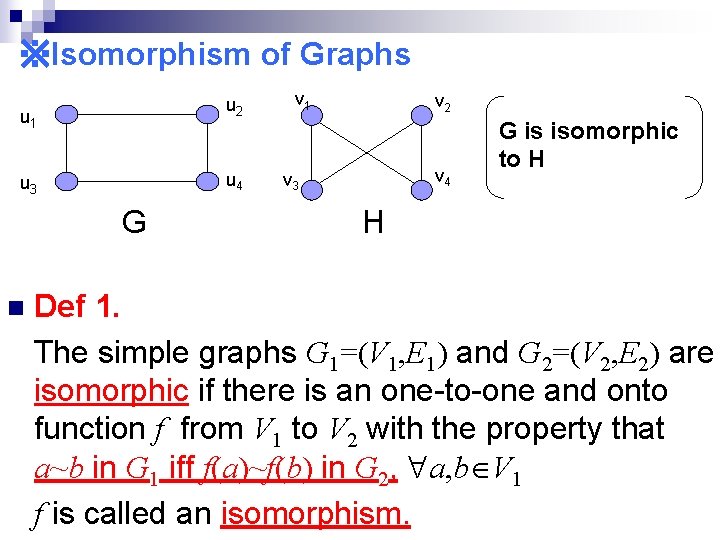
※Isomorphism of Graphs u 2 u 1 u 4 u 3 G n v 1 v 2 v 4 v 3 G is isomorphic to H H Def 1. The simple graphs G 1=(V 1, E 1) and G 2=(V 2, E 2) are isomorphic if there is an one-to-one and onto function f from V 1 to V 2 with the property that a~b in G 1 iff f(a)~f(b) in G 2, a, b V 1 f is called an isomorphism.

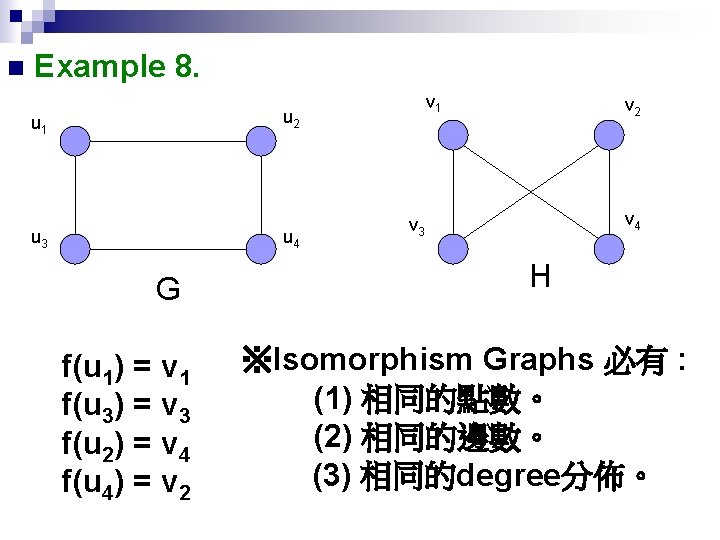
n Example 8. v 1 u 2 u 1 u 3 u 4 G f(u 1) = v 1 f(u 3) = v 3 f(u 2) = v 4 f(u 4) = v 2 v 4 v 3 H ※Isomorphism Graphs 必有 : (1) 相同的點數。 (2) 相同的邊數。 (3) 相同的degree分佈。


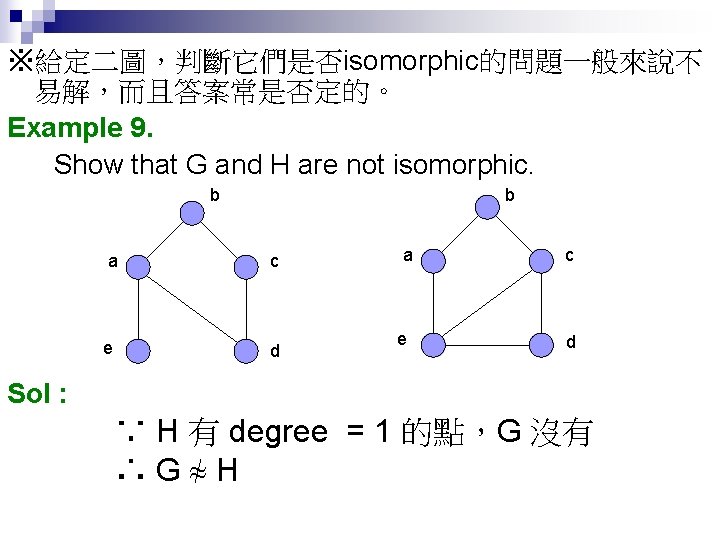
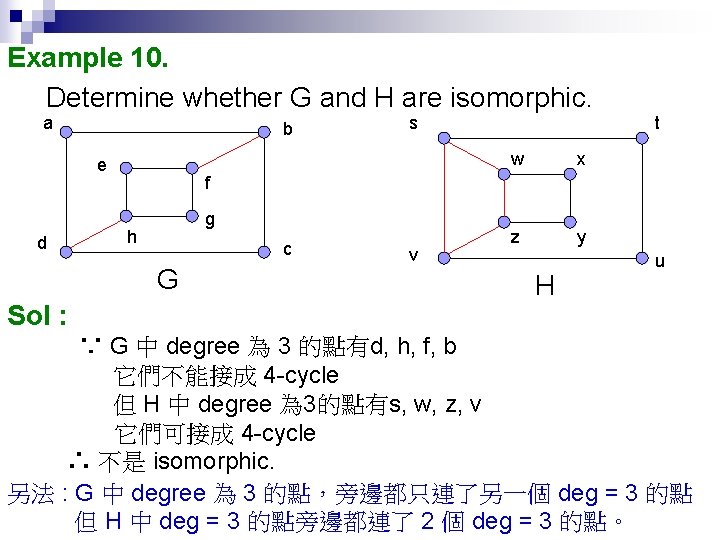
Example 10. Determine whether G and H are isomorphic. a b e d w x z y t f g h c G Sol : s v H u ∵ G 中 degree 為 3 的點有d, h, f, b 它們不能接成 4 -cycle 但 H 中 degree 為 3的點有s, w, z, v 它們可接成 4 -cycle ∴ 不是 isomorphic. 另法 : G 中 degree 為 3 的點,旁邊都只連了另一個 deg = 3 的點 但 H 中 deg = 3 的點旁邊都連了 2 個 deg = 3 的點。

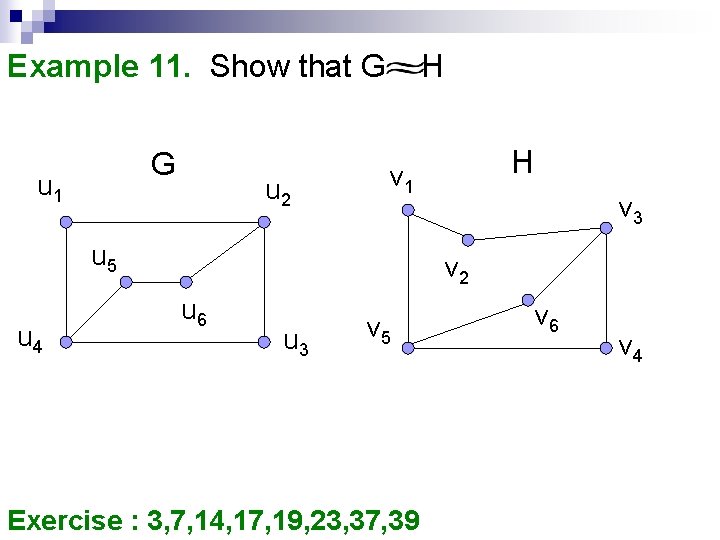
Example 11. Show that G G u 1 u 2 H u 5 u 4 H v 1 v 3 v 2 u 6 u 3 v 5 Exercise : 3, 7, 14, 17, 19, 23, 37, 39 v 6 v 4

§ 8. 4: Connectivity Def. 1, 2 : n In an undirected graph, a path of length n from u to v is a sequence of adjacent vertices going from vertex u to vertex v. (e. g. , P: u=x 0, x 1, x 2, …, xn=v) n Note. A path of length n has n+1 vertices,n edges n A path is a circuit if u=v. n A path traverses the vertices along it. n A path or circuit is simple if it contains no vertex more than once. (simple circuit通常稱為cycle)

Paths in Directed Graphs Same as in undirected graphs, but the path must go in the direction of the arrows. Figure 5. n

Connectedness Def. 3: An undirected graph is connected (連通) iff there is a path between every pair of distinct vertices in the graph. Def: Connected component: maximal connected subgraph. (一個不連通的圖 會有好幾個component) Example 6

Connectedness Def: A cut vertex separates one connected component into several components if it is removed. Def: A cut edge separates one connected component into two components if it is removed. Example 8.

Connectedness in Digraphs Def. 4: A directed graph is strongly connected iff there is a directed path from a to b for any two vertices a and b. Example 9.

Connectedness in Digraphs Def. 5: It is weakly connected iff the underlying undirected graph (i. e. , with edge directions removed) is connected. n Note strongly implies weakly but not viceversa. Example 9.

Paths & Isomorphism Note that connectedness, and the existence of a circuit or simple circuit of length k are graph invariants with respect to isomorphism. Example 12. Example 13. n

Counting Paths between Vertices Let A be the adjacency matrix of graph G. Theorem 2: The number of paths of length r from vi to vj is equal to (Ar)i, j. (The notation (M)i, j denotes mi, j where [mi, j] = M. ) Example 14. Exercise: 15, 23, 25, 26

§ 8. 5: Euler & Hamilton Paths Def. 1: n An Euler circuit in a graph G is a simple circuit containing every edge of G. n An Euler path in G is a simple path containing every edge of G. Example 1.

Useful Theorems Thm. 1: A connected multigraph has an Euler circuit iff each vertex has even degree. Thm. 2: A connected multigraph has an Euler path (but not an Euler circuit) iff it has exactly 2 vertices of odd degree. Example 4.

Hamilton Paths Def. 2: n A Hamilton circuit is a circuit that traverses each vertex in G exactly once. n A Hamilton path is a path that traverses each vertex in G exactly once. Example 5.

Useful Theorems Thm. 3 (Dirac’s Thm. ): If (but not only if) G is connected, simple, has n 3 vertices, and deg(v) n/2 v, then G has a Hamilton circuit. Exercise: 3, 5, 7, 21, 26, 28, 42, 43.

§ 8. 6: Shortest Path Problems Def: Graphs that have a number assigned to each edge are called weighted graphs. Shortest path Problem: Determining the path of least sum of the weights between two vertices in a weighted graph.

Dijkstra’s Algorithm Figure 4. Exercise: 3

§ 8. 7: Planar Graphs Def. 1: A graph is called planar if it can be drawn in the plane without any edge crossing. Example 1: K 4 is planar. Example 3: K 3, 3 is nonplanar. Exercise: 2, 3, 4

§ 8. 8: Graph Coloring Def. 1: A coloring of a simple graph is the assignment of a color to each vertex of the graph so that no two adjacent vertices are assigned the same color. Def. 2: The chromatic number of a graph is the least number of colors needed for a coloring of this graph. (denoted by c(G))

§ 8. 8: Graph Coloring Example 1 Example 2~4: c(Kn)=n, c(Km, n)=2, c(Cn)=2, 3. Example 3’: If G is a bipartite graph, c(G)=2. Theorem 1. (The Four Color Theorem) The chromatic number of a planar graph is no greater than four. Exercise: 6, 7