Counting Tools Enumeration Multiplication Addition Negation Enumeration Make

Counting Tools ● Enumeration ● Multiplication ● Addition ● Negation

Enumeration ● Make a list of the possibilities ● This is fine if the list is short!

Sum of dice is 7 or 11 ● ● Sum is 7: there are 6 ways to do it – 1, 6 or 6, 1 – 2, 5 or 5, 2 – 3, 4 or 4, 3 Sum is 11: there are 2 ways to do it – 5, 6 or 6, 5

Binary numbers ● Eight-bit strings of 0’s and 1’s with exactly one 1 – – – – 10000000 01000000 00100000 000100001000 00000100 00000010 00000001

Orderings of ABCDEFG Strings starting with A There are 6! (why? ) – you don’t want to enumerate these Strings containing ABC and CFD ABCFD must be in the string, plus E and G You can enumerate these using permutations algorithm: ABCFDEG, ABCFDGE, EABCFDG, EGABCFD, GABCFDE, GEABCFD 6 orderings Strings containing ABC, GA, and CFD GABCFD must be in the string, plus E GABCFDE, EGABCFD 2 orderings

Multiplication Principle If an activity can be constructed in t successive steps and step 1 can be done in n 1 ways, step 2 can then be done in n 2 ways, . . . , and step t can be done in nt ways, then the number of different possible activities is n 1 * n 2 *. . . * nt

License Plates ● 3 letters, 2 digits – Steps: ● – Pick first letter, Pick second letter, Pick third letter, Pick first digit, Pick second digit The number of ways depends on whether repetitions are allowed: ● ● 26*26*26*10*10 (repetitions allowed) 26*25*24*10*9 (no repetitions allowed)

Menu Selections ● 2 appetizers (opt) ● 3 main courses ● 4 beverages (opt) 3 appetizers (counting “none”) * 3 main * 5 beverages (counting “none”) = 45

Committee Assignments ● 6 person committee, 3 positions: chair, secretary, treasurer (A, B, C, D, E, and F) – Procedure: ● ● ● – Counting: ● ● ● – Step 1. Chair Step 2. Secretary Step 3. Treasurer Step 1. 6 possibilities Step 2. 5 possibilities Step 3. 4 possibilities 6*5*4 = 120

Committee Assignments ● 6 person committee {A, B, C, D, E, F} ● Subcommittees with D and not F – – – Procedure: ● Step 1: Assign D a position ● Step 2: Pick members for other positions from {A, B, C, E} Counting: ● Step 1: D can have any of three positions ● Step 2: 4*3 for the two positions left after assigning D a position 3*(4*3) = 24

Special case of the Multiplication Principle: the Odometer Principle 000001. . . 00009 00100 00101. . . 00109 00010 00011. . . 00019 00110 00111. . . 00119 . . . 00090 00091. . . 00099 . . . 00190 00191. . . 00199

Odometer Principle If you are looking at the number of ways to order n digits in same base (e. g. , 10 or 2), then the number of ways is 1 followed by n zeroes in that base.

Number of strings of digits ● ● Five digits base 10 – Multiplication principle: 10^5 – Odometer principle: 10000010 Eight digits base 2 – Multiplication principle: 2^8 – Odometer principle: 100002 = 256

Braille Letters Each dot can be raised or not 2^6 (-1 if at least one dot must be raised) Alternate view: Binary numbers from 1 to 2^6 -1

Using the constraint itself ● Eight-bit palindromes – A palindrome reads the same backwards and forwards – 1101 1011 – 2^4 = 16

Addition Principle Suppose that X 1, . . . , Xt are sets and that the ith set Xi has ni elements. If {X 1, . . . , Xt} is a pairwise disjoint family (i. e. , if i j, Xi ∩ Xj = Ф), the number of possible elements that can be selected from X 1 or X 2 or. . . or Xt is n 1 + n 2 +. . . + nt.

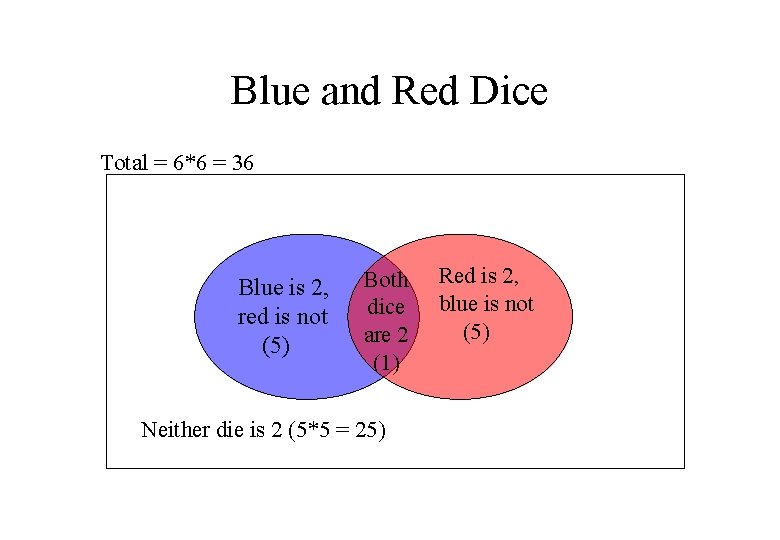
Blue and Red Dice ● Two dice show exactly one two: – Blue die is 2; red die is not 2 ● – Red die is 2; blue die is not 2 ● ● 1*5 Disjoint sets: add the results

Blue and Red Dice ● At least 1 die shows 2 – 1*6 + 1*6 – 1*6 + 1*5 1, 2 2, 2 3, 2 4, 2 5, 2 6, 2 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6

Blue and Red Dice Total = 6*6 = 36 Blue is 2, red is not (5) Both dice are 2 (1) Neither die is 2 (5*5 = 25) Red is 2, blue is not (5)

Numbers from 5 to 200 ● Numbers from 5 to 200, inclusive ● Digits must be in strictly increasing order ● How many numbers like this are there?

Numbers from 5 to 200 ● How many numbers are there? – Case 1: Numbers from 5 to 9 ● – Case 2: Numbers from 10 to 99 ● – All 5 have digits in increasing order (5) Choose two different digits, from {1, 2, …, 9}, and put them in increasing order (C(9, 2)) Case 3: Numbers from 100 to 200 ● ● The numbers will all start with 1 Choose two different digits, from {2, …, 9}, and put them in increasing order (C(8, 2))

Permutations A permutation of n distinct elements x 1, . . . , xn is an ordering of the n elements x 1, . . . , xn There are n! permutations of n elements

Permutations of a string ● ● How many permutations of ABCDEF contain the string DEF? – Permutations of the set {A, B, C, DEF} – 4! Permutations containing DB and AE? – Permutations of the set {AE, C, DB, F} – 4!

Permutations of a string ● ● Set of letters {a, b, c, d, e} How many 5 -letter strings contain either ae or ea? – Case 1: String contains ae ● ● – Case 2: String contains ea ● ● – Permutations of {ae, b, c, d} 4! Permutations of {ea, b, c, d} 4! 2*4!

Permutations of a string ● 5 -letter strings using {a, b, c, d, e} ● Containing both ab and be – “abe” must appear in the string – Permutations of {abe, c, d} – 3!

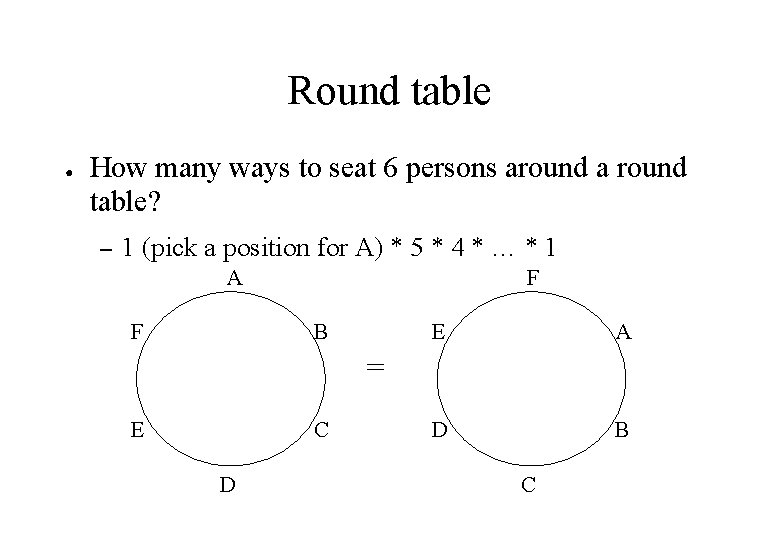
Round table ● How many ways to seat 6 persons around a round table? – 1 (pick a position for A) * 5 * 4 * … * 1 F A F B E A D B = E C D C

Strings with repetitions of letters ● ● Set of letters {a, b, c, d, e} Number of 5 -letter strings containing db and ae – Five cases ● ● ● – – db , ae, a db , ae, b db, ae, c db, ae, d db, ae, e 3! permutations in each case Total = 3! + 3! = 5*3!

Strings with repetitions of letters ● ● ● 5 -letter strings using {a, b, c, d, e} Containing both ab and be – Case 1: “abe” is in the string (75) – Case 2: There is a 4 -letter string containing “ab” and “be, ” but no 3 -letter string (i. e. , “abbe” or “beab” but not “abe”) (18) – Case 3: There is a 5 -letter string containing “ab” and “be, ” but no 4 -letter string or 3 -letter string (i. e. , “ab? be” or “be? ab” but not “abe” or “abbe” or “beab”) (8) 101 strings

Case 1 ● “abe” is in the string – – – ● Or – – ● Case 1 a: abe? ? Case 1 b: ? abe? Case 1 c: ? ? abe Step 1: Pick a starting position for abe Step 2: Choose the other two characters 3*5*5 = 75

Case 2 ● Case 2: There is a 4 -letter string containing “ab” and “be, ” but no 3 -letter string (i. e. , “abbe” or “beab” but not “abe”) – Case 2 a: abbe? or ? abbe ● – Case 2 b: beab? or ? beab ● ● 18 5 strings + 5 strings 4 strings + 4 strings

Case 3 ● There is a 5 -letter string containing “ab” and “be, ” but no 4 -letter string or 3 -letter string (i. e. , “ab? be” or “be? ab” but not “abe” or “abbe” or “beab”) – Case 3 a: ab? be ● – Case 3 b: be? ab ● ● 8 3 strings 5 strings

Strings with repetitions of letters ● Set of letters {a, b, c, d, e} ● How many 5 -letter strings contain either ae or ea? – Case 1: Containing ae (500) ● ● – Step 1: Pick a position for ae (4) Step 2: Pick the remaining letters 5^3 Case 2: Containing ea (500) ● ● Step 1: Pick a position for ea (4) Step 2: Pick the remaining letters 5^3

Strings with repetitions of letters – Case 3: Containing both ae and ea (90) ● ● ● ● aea? ? : 25 possibilities ? aea? : 25 possibilities ? ? aea : 25 possibilities – 1 (for overlap with case 3 a) aeea? : 5 possibilities eaae? : 5 possibilities – 1 (for overlap with case 3 c) ae? ea : 5 possibilities – 2 (for overlap with case 3 a and 3 c) ea? ae : 5 possibilities – 1 (for overlap with case 3 b)

Strings with repetitions of letters Total = 5^5 = 3125 Contains “ae” but not “ea” (410) Both (90) Contains “ea” but not “ae” (410) Contains neither: 3125 – 910 = 2215

r-Permutations An r-permutation of n (distinct) elements x 1, . . . , xn is an ordering of an r-element subset of {x 1, . . . , xn}. The number of r-permutations of a set of n distinct elements is denoted P(n, r) = n * (n-1) *. . . * (n-r+1) = n!/(n-r)!

● 3 -permutations of 4 letters: – ● 4*3*2 5 -permutations of 11 objects: – 11*10*9*8*7

r-Combinations An r-combination of X is an unordered selection of relement subsets of X The number of r-combinations of a set of n distinct elements is denoted C(n, r) or ( )

Committees and Sub-committees ● Club: 6 women and 6 men ● Committee of 5 persons ● C(12, 5) ● Committee of 4, and exactly 1 is a woman – C(6, 1) to pick the woman – C(6, 3) to pick the men – C(6, 1)*C(6, 3)

Committees and Sub-committees ● Four person with at least one man and one woman – All-male committee C(6, 4) – All-female committee C(6, 4) – C(12, 4) – 2*C(6, 4)

Poker Hands ● ● ● All Aces: – Step 1: Pick the aces (C(4, 4)) – Step 2: Pick the other cards (C(48, 1)) Four of a kind – Step 1: Pick which kind (13 ways) – Step 2: Pick which suits (C(4, 4)) – Step 3: Pick the other cards (C(48, 1)) All spades – C(13, 5)

Poker Hands ● Cards of two suits – Pick the two suits C(4, 2) – Pick the cards C(26, 5) – Subtract the hands containing only 1 suit 2*C(13, 5)

Negation The number of possibilities with constraint X is equal to the possibilities with no constraints minus the possibilities with constraint “not X. ” This is a special case of the addition principle.

Binary numbers ● Eight bit string, with at least one 1 – The only string that doesn’t have at least one 1 is 0000 – 2^8 - 1

Braille Letters Each dot can be raised or not 2^6 -1 since at least one dot must be raised Alternate view: Binary numbers from 1 to 2^6 -1

Poker Hands ● Containing cards of more than one suit ● Not (containing cards of one suit) – Cards of one suit ● ● Step 1. Pick the suit C(4, 1) Step 2. Pick the cards C(13, 5) ● All possible hands: C(52, 5) ● Cards of more than one suit: C(52, 5) – C(4, 1)*C(13, 5)

Permutations ● ● Orderings of ABCDEF not containing DEF – Orderings of ABCDEF containing DEF: 4! – All orderings of ABCDEF: 6! Orderings not containing DEF: 6! – 4!

Subcommittees ● ● Group has 6 men, 6 women Subcommittees containing at least one man and one woman – Not (subcommittees of a single sex) ● ● Step 1. Pick the sex C(2, 1) Step 2. Pick the members C(6, 4) ● All subcommittees C(12, 4) ● At least 1 man and 1 woman: C(12, 4) – C(2, 1)*C(6, 4)

Summary ● Enumeration: for small numbers of things ● Multiplication principle: define steps ● Addition principle: define distinct cases ● “Negation” approach: how many x don’t have the property? ● Permutations: sequences (order is important) ● Combinations: sets (ignore order)

Algorithm for combinations ● ● ● 4 -combinations of {1, 2, 3, 4, 5, 6, 7} Problem 1: How do we avoid repeating the same set, since order doesn’t matter – Generate the elements in increasing order Problem 2: What is the first combination? – {1, 2, 3, 4} Problem 3: How do we generate the next element from the current one? Problem 4: What is the last combination? – {4, 5, 6, 7}

Algorithm for Combinations ● Try it by hand: – 1234 – 1235 – 1236 – 1237 – 1245 – 1246 – 1247 – 1256 – 1257 – 1267 – 1345 – 1346

Algorithm for Combinations ● Step 1: Find last (rightmost) item (sm) that’s not equal to its maximum value and add one to it. – Maximum value: ● ● ● for sr the maximum is n for sr-i the maximum is n-i Step 2: For the remaining items (to the right of sm), let si = si-1 + 1

Algorithm for Permutations ● ● Note that order matters, so we don’t have to worry about repeating Problem 1: What is the first permutation? – ● ● 1…n Problem 2: How do we generate the next permutation from the current one? Problem 3: What is the last permutation? – n… 1

Algorithm for Permutations ● Try it by hand: – – – 12345 12354 12435 12453 12534 12543 13245 13254 13425 13452 13524 13542

Algorithm for Permutations ● ● Step 1: Locate the rightmost sm such that sm < sm+1 (entries sm+1 … sn are in decreasing order) Step 2: Locate the rightmost (last) si after sm such that sm < si Step 3: Swap sm and si (entries sm+1 … sn are still in decreasing order) Step 4: Reverse the order of sm+1 … sn

Recursive algorithm ● Create a list 12…n ● For each element i in the list ● – Generate the set of permutations of the remaining elements – Return the set of permutations formed by appending the element i to the permutation Base case: Only 1 element in the list – return the set of permutations containing the list

Two more tools for counting Generalized permutations: to count orderings of a string containing multiple identical letters: n! / (n 1!*…*nt!) Generalized combinations: to count the number of ways to put n identical things into k distinct groups C(n+k-1, k-1)

MISSISSIPPI How many strings can be formed from the above letters? Solution: Fill 11 blanks ______ Step 1. Step 2. Step 3. Step 4. Pick the positions for the S’s Pick the positions for the I’s Pick the positions for the P’s Put the M in the remaining position

Counting the ways… Step 1. Pick the positions for the S’s Step 2. Pick the positions for the I’s Step 3. Pick the positions for the P’s Step 4. Put the M in the remaining position C(11, 4) C(7, 4) C(3, 2) C(1, 1) C(11, 4)*C(7, 4)*C(3, 2)*C(1, 1) =

Counting sequences with identical objects Suppose that a sequence S of n items has n 1 identical objects of type 1, n 2 identical objects of type 2, …, and nt identical objects of type t. Then the number of orderings of S is n!____ n 1! n 2! … nt!

Using equivalence relations M, I 1, S 2, I 2, S 3, S 4, I 3, P 1, P 2, I 4 Define R: Let p and q be permutations of the above string. p. Rq if the letter in each position of the two permutations is the same (ignore the number) How many members in each equivalence class? Pick any permutation – how many ways to reorder it so that the same letters appear in the same positions?

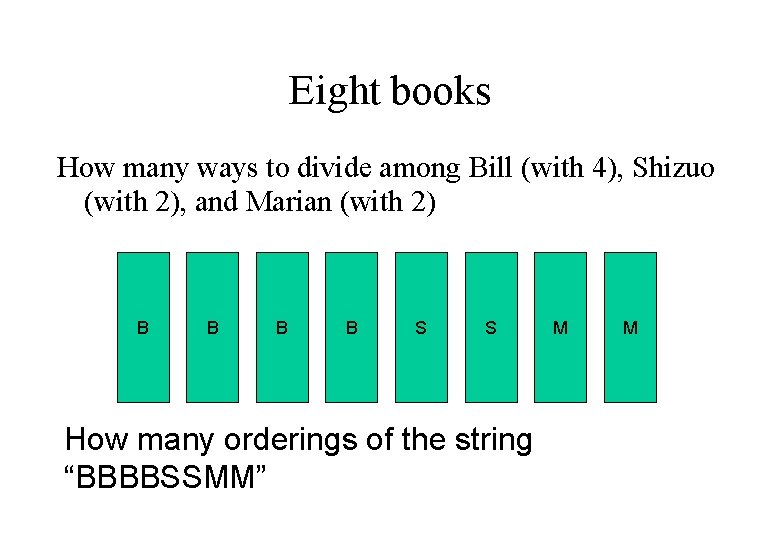
Eight books How many ways to divide among Bill (with 4), Shizuo (with 2), and Marian (with 2) B B S S How many orderings of the string “BBBBSSMM” M M

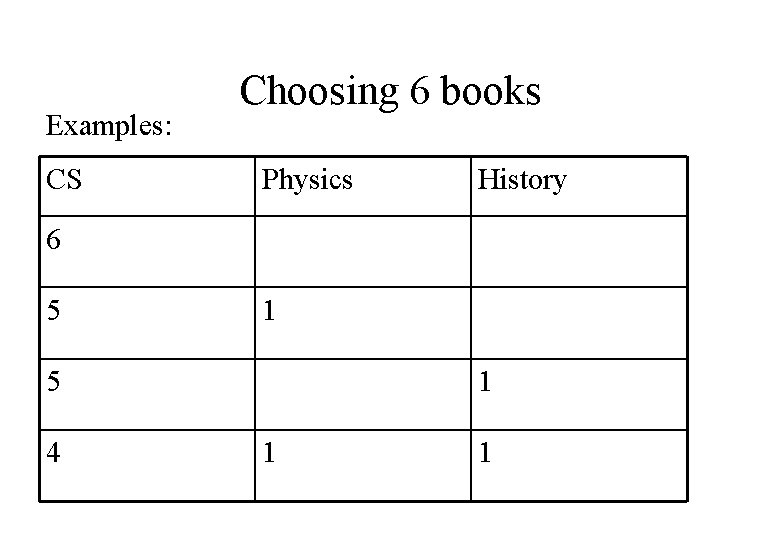
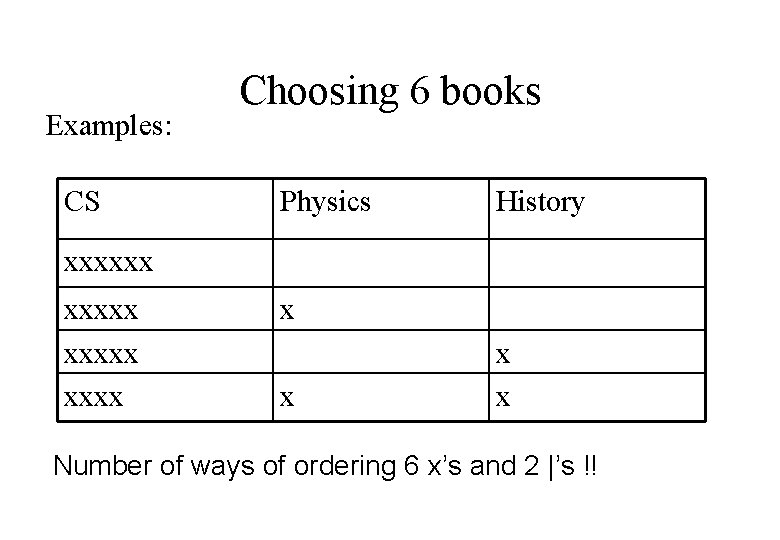
Choosing six books Three books: CS, Physics, History Library has at least 6 of each How many ways can we choose 6?

Examples: CS Choosing 6 books Physics History 6 5 1 5 4 1 1 1

Examples: CS Choosing 6 books Physics History xxxxxx x x Number of ways of ordering 6 x’s and 2 |’s !!

Building sets by choosing identical elements If X is a set containing t elements, the number of unordered, k-element selections from X, repetitions allowed, is C(k+t-1, t-1) = C(k+t-1, k).

Red, Green, Blue Balls ● ● How many ways can we select 8 balls with at least one of each color?

12 identical math books Distributed among Anna, Beth, Candy, and Don

Solutions to equation x 1 + x 2 + x 3 + x 4 = 29 if x 1, x 2, x 3, x 4 are nonnegative integers? If x 1 > 0, x 2 > 1, x 3 > 2, x 4 >= 0?

How many times is the print statement executed? For i 1 : = 1 to n do for i 2 : = 1 to i 1 do for i 3 : = 1 to i 2 do for ik : = 1 to ik-1 do print i 1, …, ik