MATRIKS RELASI FUNGSI Nelly Indriani W Matematika Diskrit

MATRIKS, RELASI & FUNGSI Nelly Indriani W. Matematika Diskrit IF UNIKOM 1

MATRIKS • Susunan skalar elemen-elemen yang terdiri dari baris dan kolom • A mxn , m baris dan n kolom 2

JENIS – JENIS MATRIKS v. Matriks Segitiga v. Matriks Diagonal v. Matriks Identitas v. Matriks Komutatif v. Matriks Invers 3

Matriks Segitiga Untuk setiap matriks persegi A berdimensi nxn • Matriks segitiga atas, jika untuk semua i > j, aij = 0. A = B = C = • Matriks segitiga bawah, jika untuk semua i < j, aij = 0. A = H = K = 4

Matriks Diagonal Matriks persegi A berdimensi nxn dengan aij = 0 untuk semua i > j dan i < j. D = diag(d 11, d 22, …, dnn) Atau D = diag(4, 7, 0, -5) Jika D = diag(d 11, d 22, …, dnn) dengan d 11 = d 22 = … = dnn = k, maka matriksnya disebut matriks skalar S = 5

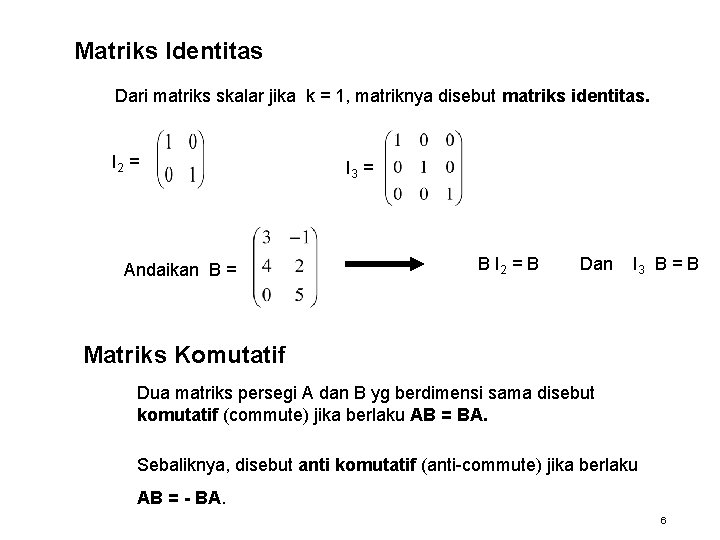
Matriks Identitas Dari matriks skalar jika k = 1, matriknya disebut matriks identitas. I 2 = Andaikan B = I 3 = B I 2 = B Dan I 3 B = B Matriks Komutatif Dua matriks persegi A dan B yg berdimensi sama disebut komutatif (commute) jika berlaku AB = BA. Sebaliknya, disebut anti komutatif (anti-commute) jika berlaku AB = - BA. 6

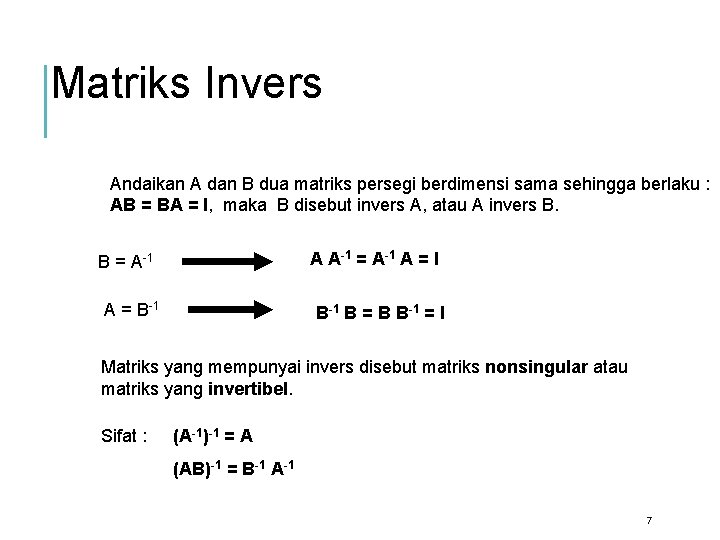
Matriks Invers Andaikan A dan B dua matriks persegi berdimensi sama sehingga berlaku : AB = BA = I, maka B disebut invers A, atau A invers B. A A-1 = A-1 A = I B = A-1 A = B-1 B = B B-1 = I Matriks yang mempunyai invers disebut matriks nonsingular atau matriks yang invertibel. Sifat : (A-1)-1 = A (AB)-1 = B-1 A-1 7

Tranpose Matriks A = (aij) berdimensi mxn, tranposenya adalah AT = (aji) yg berdimensi nxm. Sifat-sifat : 1. (AT)T = A 2. (A + B)T = AT + BT 3. (AB)T = BT AT 8

RELASI Relasi biner R antara himpunan A dan B adalah himpunan bagian dari A B. a R b , untuk (a, b) R a dihubungankan dengan b oleh R. a R b , untuk (a, b) R a tidak dihubungkan dengan b oleh relasi R. 9

CONTOH : A = {Amir, Budi, Cecep}, B = {IF 221, IF 251, IF 342, IF 323} A B = {(Amir, IF 221), (Amir, IF 251), (Amir, IF 342), (Amir, IF 323), (Budi, IF 221), (Budi, IF 251), (Budi, IF 342), (Budi, IF 323), (Cecep, IF 221), (Cecep, IF 251), (Cecep, IF 342), (Cecep, IF 323) } 10

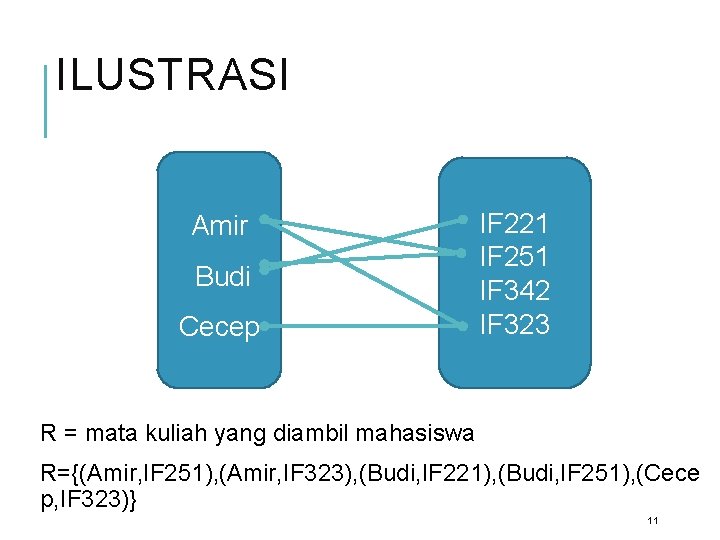
ILUSTRASI Amir Budi Cecep IF 221 IF 251 IF 342 IF 323 R = mata kuliah yang diambil mahasiswa R={(Amir, IF 251), (Amir, IF 323), (Budi, IF 221), (Budi, IF 251), (Cece p, IF 323)} 11

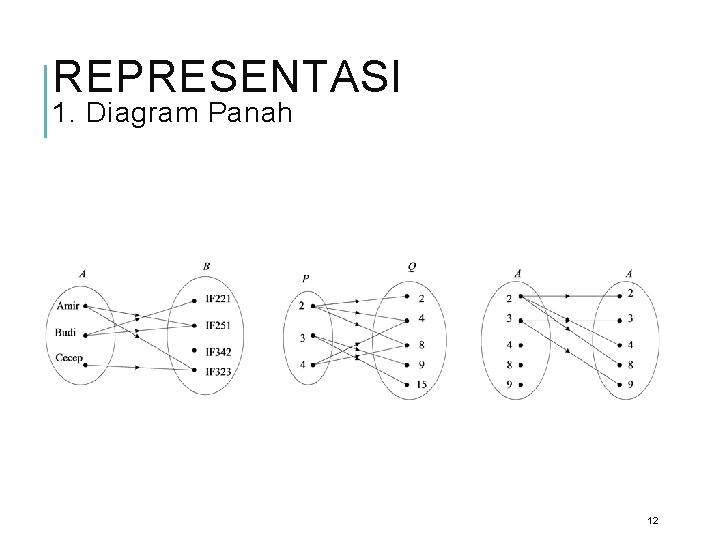
REPRESENTASI 1. Diagram Panah 12

2. Tabel 13

3. MATRIKS Misalkan R adalah relasi dari A = {a 1, a 2, …, am} dan B = {b 1, b 2, …, bn}. Relasi R dapat disajikan dengan matriks M = [mij], 14

4. GRAF BERARAH Jika (a, b) R, maka sebuah busur dibuat dari simpul a ke simpul b. Simpul a disebut simpul asal (initial vertex) dan simpul b disebut simpul tujuan (terminal vertex). Pasangan terurut (a, a) dinyatakan dengan busur dari simpul a ke simpul a sendiri. Busur semacam itu disebut gelang atau kalang (loop). 15

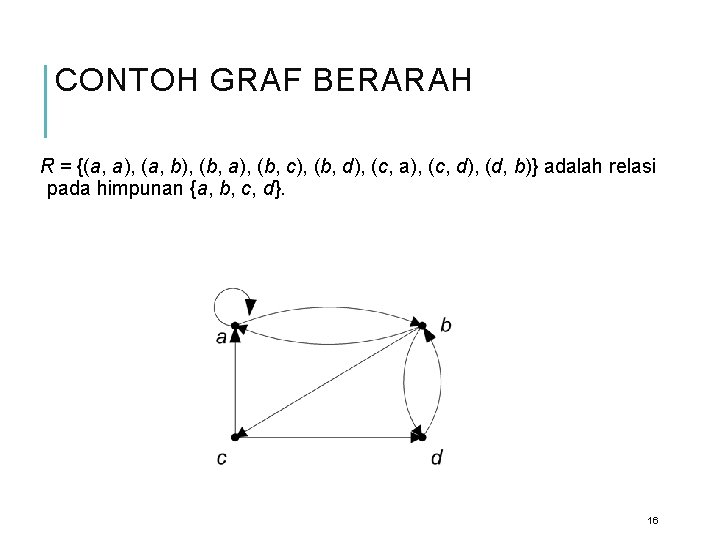
CONTOH GRAF BERARAH R = {(a, a), (a, b), (b, a), (b, c), (b, d), (c, a), (c, d), (d, b)} adalah relasi pada himpunan {a, b, c, d}. 16

SIFAT RELASI v. Reflexive v. Transitive v. Symmetric v. Antisymmentric v. Invers 17

REFLEXIVE Jika (a, a) R untuk setiap a A maka refleksif Tidak refleksif jika ada a A sedemikian sehingga (a, a) R. A={1, 2, 3, 4} Contoh : R 2 = {(1, 1), (1, 3), (2, 1), (2, 2), (3, 3), (4, 2), (4, 3), (4, 4)} R 2= {(1, 1), (2, 2), (2, 3), (4, 2), (4, 3), (4, 4) } Matriks relasi yang refleksif Graf memiliki loop pada tiap simpul 18

TRANSITIVE (MENGHANTAR) Jika (a, b) R dan (b, c) R, maka (a, c) R, untuk a, b, c A. A={1, 2, 3, 4} Contoh : R 1 = {(2, 1), (3, 2), (4, 1), (4, 2), (4, 3) } R 2= {(1, 1), (2, 3), (2, 4), (4, 2)} Relasi R = {(1, 1), (2, 2), (3, 3), (4, 4) } menghantar Relasi R = {(1, 2), (3, 4)} menghantar R = {(3, 4)} selalu menghantar 19

SYMMETRIC (SETANGKUP) Jika (a, b) R, maka (b, a) R. Tidak setangkup, jika (a, b) R sedemikian sehingga (b, a) R. Elemen-elemen matriks diantara diagonal utama merupakan hasil pencerminan , atau mij = mji = 1, untuk i = 1, 2, …, n 20

ANTISYMMETRIC (TOLAK SETANGKUP) Jika untuk semua a, b A, (a, b) R dan (b, a) R hanya jika a = b Tidak tolak-setangkup jika ada elemen berbeda a dan b sedemikian sehingga (a, b) R dan (b, a) R. Matriks jika mij = 1 dengan i j, maka mji = 0 matriks dari relasi tolak-setangkup adalah jika salah satu dari mij = 0 atau mji = 0 bila i j 21

CONTOH R 1 = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 4), (4, 2), (4, 4) } setangkup R 2 = {(1, 1), (2, 3), (2, 4), (4, 2) } tidak setangkup R 3 = {(1, 1), (2, 2), (3, 3) } tolak-setangkup R 4 = {(1, 1), (1, 2), (2, 3)} tolak-setangkup R 5 = {(1, 1), (2, 4), (3, 3), (4, 2) } tidak tolak-setangkup R 6 = {(1, 2), (2, 3), (1, 3) } tidak setangkup dan juga tolak-setangkup R 7 = {(1, 1), (2, 2), (2, 3), (3, 2), (4, 4)} tidak setangkup maupun tidak tolak-setangkup 22

INVERSI R– 1 = {(b, a) | (a, b) R } Contoh : P = {2, 3, 4} dan Q = {2, 4, 8, 9, 15}. (p, q) R jika p habis membagi q maka R = {(2, 2), (2, 4), (4, 4), (2, 8), (4, 8), (3, 9), (3, 15) } R– 1 adalah invers dari relasi R, yaitu Q ke P dengan (q, p) E R– 1 jika q kelipatan dari p 23

KLOSUR RELASI (CLOSURE OF RELATION) Misalkan R adalah relasi pada himpunan A. R dapat memiliki atau tidak memiliki sifat P, seperti refleksif, setangkup, atau menghantar. Jika terdapat relasi S dengan sifat P yang mengandung R sedemikian sehingga S adalah himpunan bagian dari setiap relasi dengan sifat P yang mengandung R, maka S disebut klosur (closure) atau tutupan dari R [ROS 03]. 24

KLOSUR REFLEKSIF Misalkan R adalah sebuah relasi pada himpunan A. Klosur refleksif dari R adalah R , yang dalam hal ini = {(a, a) | a A}. 25

Conto h: R = {(1, 1), (1, 3), (2, 3), (3, 2)} adalah relasi pada A = {1, 2, 3} maka = {(1, 1), (2, 2), (3, 3)}, sehingga klosur refleksif dari R adalah R = {(1, 1), (1, 3), (2, 3), (3, 2)} {(1, 1), (2, 2), (3, 3)} = {(1, 1), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3)} 26

Contoh: Misalkan R adalah relasi {(a, b) | a b} pada himpunan bilangan bulat. Klosur refleksif dari R adalah R = {(a, b) | a b} {(a, a) | a Z} = {(a, b) | a, b Z} 27

Contoh 1: Relasi R = {(1, 1), (1, 3), (2, 3), (3, 2)} pada himpunan A = {1, 2, 3} tidak refleksif. Bagaimana membuat relasi refleksif yang sesedikit mungkin dan mengandung R? 28

Tambahkan (2, 2) dan (3, 3) ke dalam R (karena dua elemen relasi ini yang belum terdapat di dalam R) Relasi baru, S, mengandung R, yaitu S = {(1, 1), (1, 3), (2, 2), (2, 3), (3, 2), (3, 3) } Relasi S disebut klosur refleksif (reflexive closure) dari R. 29

KLOSUR SETANGKUP Misalkan R adalah sebuah relasi pada himpunan A. Klosur setangkup dari R adalah R R-1, dengan R-1 = {(b, a) | (a, b) a R}. 30

Contoh: R = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} adalah relasi pada A = {1, 2, 3}, maka R-1 = {(3, 1), (2, 1), (1, 2), (2, 3), (3, 3)} sehingga klosur setangkup dari R adalah R R-1 = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} {(3, 1), (2, 1), (1, 2), (2, 3), (3, 3)} ={(1, 3), (3, 1), (1, 2), (2, 1), (3, 2), (2, 3), (3, 3)} 31

Contoh 2: Relasi R = {(1, 3), (1, 2), (2, 1), (3, 2), (3, 3)} pada himpunan A = {1, 2, 3} tidak setangkup. Bagaimana membuat relasi setangkup yang sesedikit mungkin dan mengandung R? 32

Tambahkan (3, 1) dan (2, 3) ke dalam R (karena dua elemen relasi ini yang belum terdapat di dalam S agar S menjadi setangkup). Relasi baru, S, mengandung R: S = {(1, 3), (3, 1), (1, 2), (2, 1), (3, 2), (2, 3), (3, 3)} Relasi S disebut klosur setangkup (symmetric closure) dari R. 33

Contoh: Misalkan R adalah relasi {(a, b) | a habis membagi b} pada himpunan bilangan bulat. Klosur setangkup dari R adalah R R-1 = {(a, b)|a habis membagi b} {(b, a)|b habis membagi a} = {(a, b) | a habis membagi b atau b habis membagi a} 34

KLOSUR MENGHANTAR Contoh: R = {(1, 2), (1, 4), (2, 1), (3, 2)} adalah relasi A = {1, 2, 3, 4}. R tidak transitif karena tidak mengandung semua pasangan (a, c) sedemikian sehingga (a, b) dan (b, c) di dalam R. Pasangan (a, c) yang tidak terdapat di dalam R adalah (1, 1), (2, 2), (2, 4), dan (3, 1). 35

Penambahan semua pasangan ini ke dalam R sehingga menjadi S = {(1, 2), (1, 4), (2, 1), (3, 2), (1, 1), (2, 2), (2, 4), (3, 1)} tidak menghasilkan relasi yang bersifat menghantar karena, misalnya terdapat (3, 1) S dan (1, 4) S, tetapi (3, 4) S. 36

Klosur menghantar dari R adalah R* = R 2 R 3 … Rn Jika MR adalah matriks yang merepresentasikan R pada sebuah himpunan dengan n elemen, maka matriks klosur menghantar R* adalah 37

KOMBINASI RELASI Jika R 1 dan R 2 masing-masing adalah relasi dari himpunan A ke himpunan B, maka R 1 R 2 , R 1 R 2, R 1 – R 2, dan R 1 R 2 juga adalah relasi dari A ke B 38

CONTOH A = {a, b, c} dan B = {a, b, c, d}. Relasi R 1 = {(a, a), (b, b), (c, c)} Relasi R 2 = {(a, a), (a, b), (a, c), (a, d)} R 1 R 2 = R 2 R 1 = R 1 R 2 = 39

KOMBINASI RELASI DALAM MATRIKS Jika relasi R 1 dan R 2 dinyatakan dengan matriks MR 1 dan MR 2 maka MR 1 R 2 = MR 1 MR 2 40

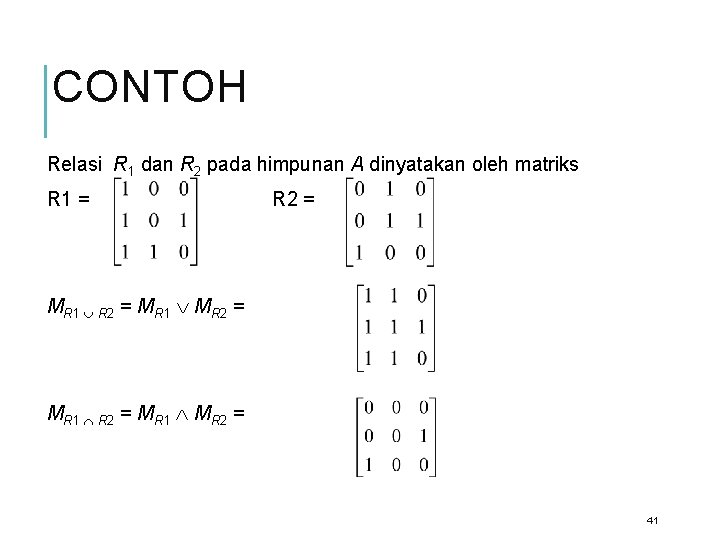
CONTOH Relasi R 1 dan R 2 pada himpunan A dinyatakan oleh matriks R 1 = R 2 = MR 1 MR 2 = 41

KOMPOSISI RELASI R adalah relasi dari himpunan A ke himpunan B, S adalah relasi dari himpunan B ke himpunan C. Komposisi R dan S, dinotasikan dengan S R, adalah relasi dari A ke C yang didefinisikan oleh S R = {(a, c ) a A, c C, dan untuk beberapa b B, (a, b ) R dan (b, c ) S } 42

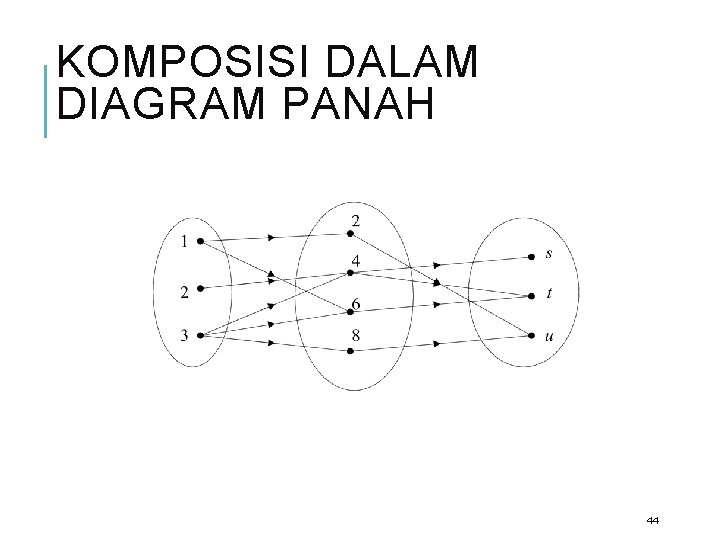
CONTOH R = {(1, 2), (1, 6), (2, 4), (3, 6), (3, 8)} adalah relasi dari {1, 2, 3} ke {2, 4, 6, 8} dan S = {(2, u), (4, s), (4, t), (6, t), (8, u)} relasi dari {2, 4, 6, 8} ke {s, t, u}. Maka komposisi relasi R dan S adalah S R = {(1, u), (1, t), (2, s), (2, t), (3, s), (3, t), (3, u) } 43

KOMPOSISI DALAM DIAGRAM PANAH 44

KOMPOSISI DALAM MATRIKS Jika relasi R 1 dan R 2 dinyatakan dengan matriks MR 1 dan MR 2, maka komposisi dari kedua relasi tersebut adalah MR 2 R 1 = MR 1 MR 2 45

CONTOH R 1 = R 2 = R 2 R 1 adalah MR 2 R 1 = MR 1. MR 2 = = 46

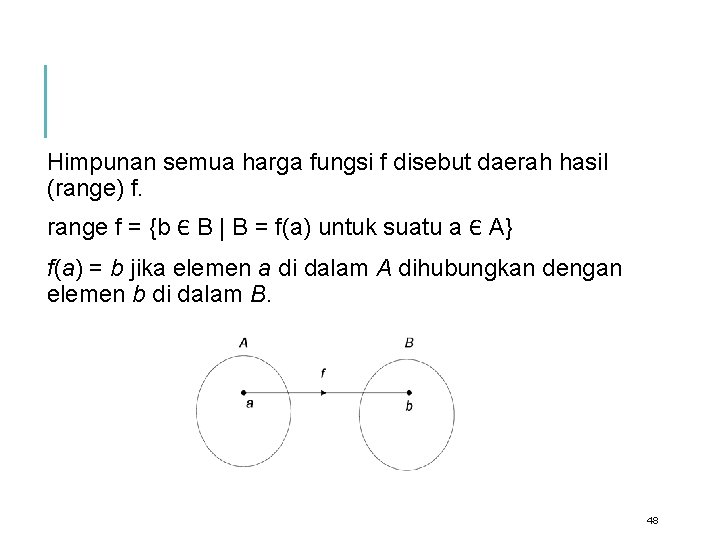
FUNGSI A dan B adalah himpunan Relasi biner f dari A ke B adalah fungsi jika setiap elemen di dalam A dihubungkan dengan tepat satu elemen di dalam B. f : A B f memetakan A ke B. A : daerah asal (domain) dari f B : daerah hasil (codomain) dari f. 47

Himpunan semua harga fungsi f disebut daerah hasil (range) f. range f = {b Є B | B = f(a) untuk suatu a Є A} f(a) = b jika elemen a di dalam A dihubungkan dengan elemen b di dalam B. 48

SYARAT Agar suatu relasi f dari X ke Y menjadi fungsi, maka harus dipenuhi : 1. 2. Setiap elemen x Є X mempunyai kawan di Y (disebut f(x)). f(x) tunggal 49

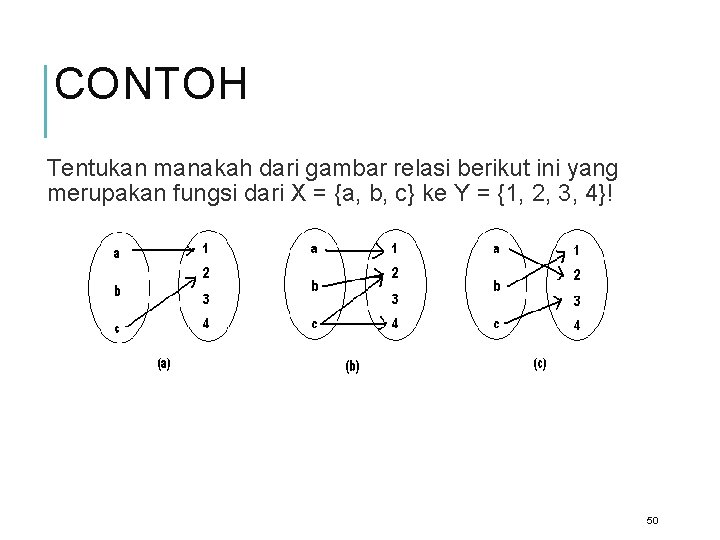
CONTOH Tentukan manakah dari gambar relasi berikut ini yang merupakan fungsi dari X = {a, b, c} ke Y = {1, 2, 3, 4}! 50

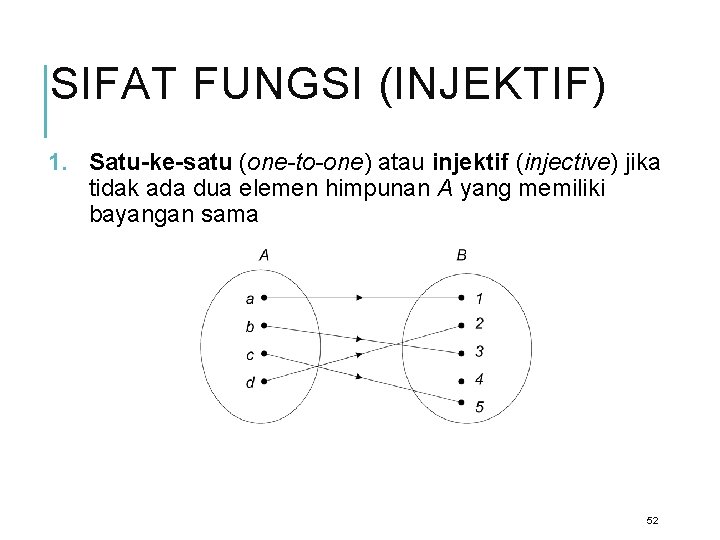
SIFAT FUNGSI (INJEKTIF) 1. Satu-ke-satu (one-to-one) atau injektif (injective) jika tidak ada dua elemen himpunan A yang memiliki bayangan sama 52

CONTOH A = {1, 2, 3} ke B = {u, v, w, x} f = {(1, w), (2, u), (3, v)} adalah fungsi satu-ke-satu A = {1, 2, 3} ke B = {u, v, w} f = {(1, u), (2, u), (3, v)} bukan fungsi satu-ke-satu, karena f(1) = f(2) = u. 53

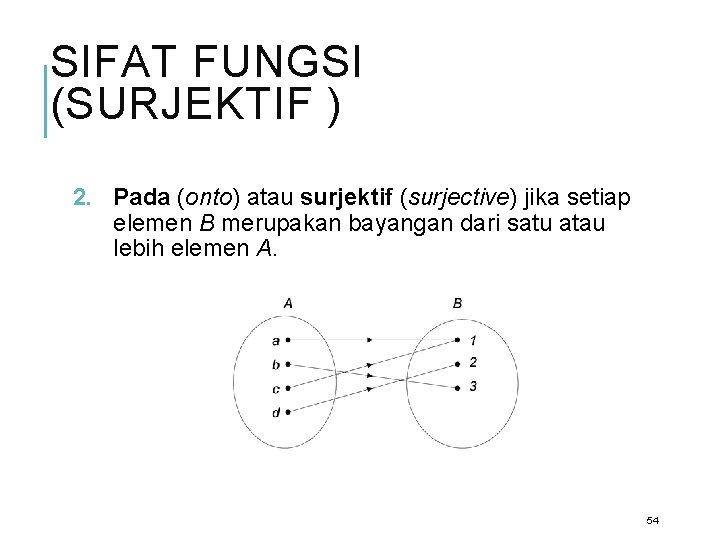
SIFAT FUNGSI (SURJEKTIF ) 2. Pada (onto) atau surjektif (surjective) jika setiap elemen B merupakan bayangan dari satu atau lebih elemen A. 54

CONTOH SURJEKTIF A = {1, 2, 3} ke B = {u, v, w} f = {(1, u), (2, u), (3, v)} bukan fungsi pada karena w tidak termasuk jelajah dari f. A = {1, 2, 3} ke B = {u, v, w} f = {(1, w), (2, u), (3, v)} fungsi pada karena semua anggota B merupakan jelajah dari f. 55

SIFAT FUNGSI (BIJEKSI) berkoresponden satu-ke-satu atau bijeksi (bijection) jika ia fungsi satu-ke-satu dan juga fungsi pada 56

FUNGSI INVERS Misalkan f : X Y adalah suatu fungsi. Relasi dari Y ke X belum tentu pula merupakan fungsi. Jika f : X Y merupakan suatu fungsi Bijektif, maka relasi Y ke X juga merupakan fungsi. Jadi dengan demikian, fungsi tersebut dapat diinvers. f(x) = y f-1(1) = k 1; f-1(3) = k 3; f-1(y) = x f-1(2) = k 3; f-1(3) = k 4 57

CONTOH FUNGSI INVERS Tentukan balikan fungsi f(x) = x – 1. Penyelesaian: Fungsi f(x) = x – 1 adalah fungsi yang berkoresponden satu -ke-satu, jadi balikan fungsi tersebut ada. Misalkan f(x) = y, sehingga y = x – 1, maka x = y + 1. Jadi, balikan fungsi balikannya adalah f-1(y) = y +1. 58

KOMPOSISI FUNGSI Komposisi fungsi (dinotasikan dengan “o”), digunakan untuk menghasilkan fungsi baru dari beberapa fungsi. Misalkan : f : X Y dan g : Y Z didefinisikan dengan komposisi fungsi f dan g (simbol gof) sebagai berikut : ( x Є X) (gof)(x) = g(f(x)) invers : (gof)-1(x) = f-1 og-1(x) = f-1(g-1(x)) 59

CONTOH KOMPOSISI FUNGSI Misalkan f dan g adalah fungsi-fungsi pada himpunan bilangan bulat Z yang didefinisikan dengan rumus f(n) = n + 1 dan g(n) = n 2 , n Є Z. Hitunglah (gof)(n), (fof)(n), dan (fog)(n)! Jawab : a. (gof)(n) = g(f(n)) = (n+1)2 b. (fof)(n) = ? c. (fog)(n) = ? 60

FUNGSI KHUSUS 1. Floor Misalkan f : R (real) adalah fungsi yang didefinisikan sebagai berikut : f(x) = |_x_| = bilangan bulat terkecil yang kurang atau sama dengan x. maka f disebut fungsi floor. Contoh : f(3, 23) = 3 ; f(5, 87) = 5 ; f(-4, 29) = ? 61

2. Ceiling Misalkan f : R (real) adalah fungsi yang didefinisikan sebagai berikut : f(x) = = bilangan bulat terbesar yang lebih atau sama dengan x maka f disebut fungsi ceiling. Contoh : f(3, 23) = 4 ; f(5, 87) = 6 ; f(-4, 29) = ? 62

Fungsi modulo 3. Fungsi modulo a mod m memberikan sisa pembagian bilangan bulat bila a dibagi dengan m a mod m = r sedemikian sehingga a = mq + r, dengan 0 r < m. Contoh : o 25 mod 7 = 4 o 16 mod 4 = 0 o 3612 mod 45 = 12 o 0 mod 5 = 0 63

FUNGSI-FUNGSI LAIN 4. Fungsi Faktorial 5. Fungsi Eksponensial 6. Fungsi Logaritmik 7. Fungsi Rekursif 8. Fungsi Chebysev 9. Fungsi Fibonnaci 64

65