8 FUNGSI TRANSENDEN 8 1 Fungsi Invers Misalkan

8. FUNGSI TRANSENDEN

8. 1 Fungsi Invers Misalkan dengan u fungsi y = x satu-satu fungsi y=-x satu-satu v fungsi tidak satu-satu

Secara geometri, grafik fungsi satu-satu dan garis yang sejajar dengan sumbu x berpotongan di satu titik. Teorema 8. 1 : Fungsi f mempunyai invers jika dan hanya jika f satu-satu. Notasi : R Df x Berlaku hubungan R f Rf y = f(x)

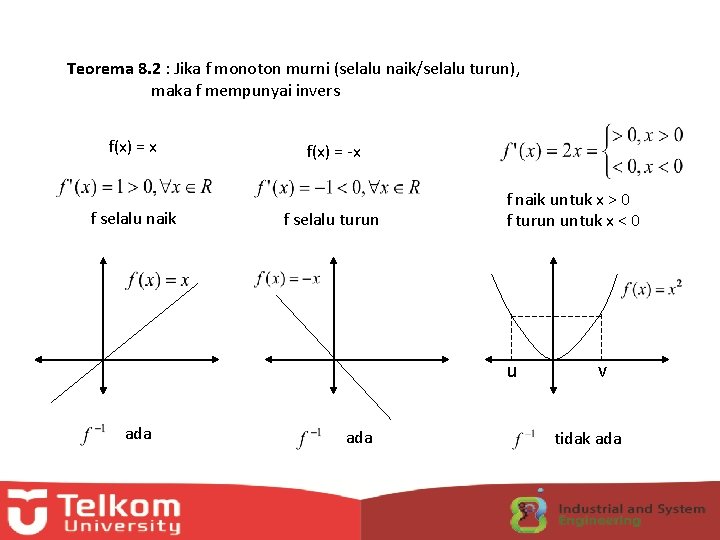
Teorema 8. 2 : Jika f monoton murni (selalu naik/selalu turun), maka f mempunyai invers f(x) = x f selalu naik f(x) = -x f selalu turun f naik untuk x > 0 f turun untuk x < 0 u ada v tidak ada

Contoh 1 : Diketahui a. Periksa apakah f mempunyai invers? b. Jika ada, tentukan inversnya ! Jawab: a. Karena f selalu naik (monoton murni), maka f mempunyai invers b. Misal

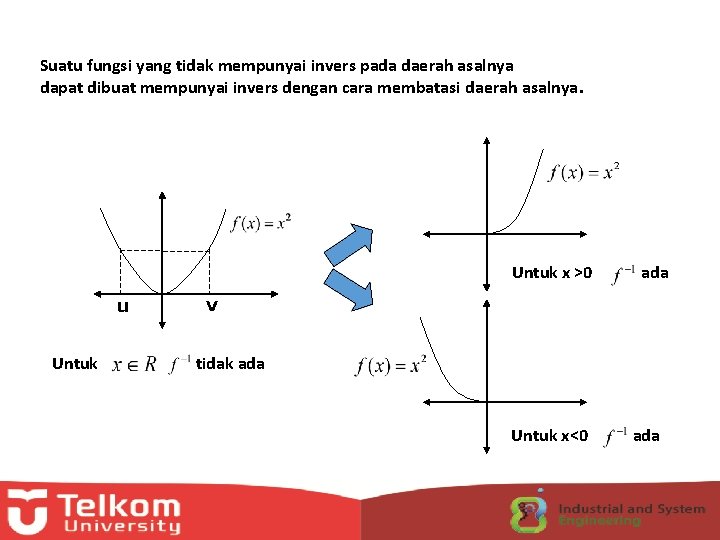
Suatu fungsi yang tidak mempunyai invers pada daerah asalnya dapat dibuat mempunyai invers dengan cara membatasi daerah asalnya. Untuk x >0 u Untuk ada v tidak ada Untuk x<0 ada

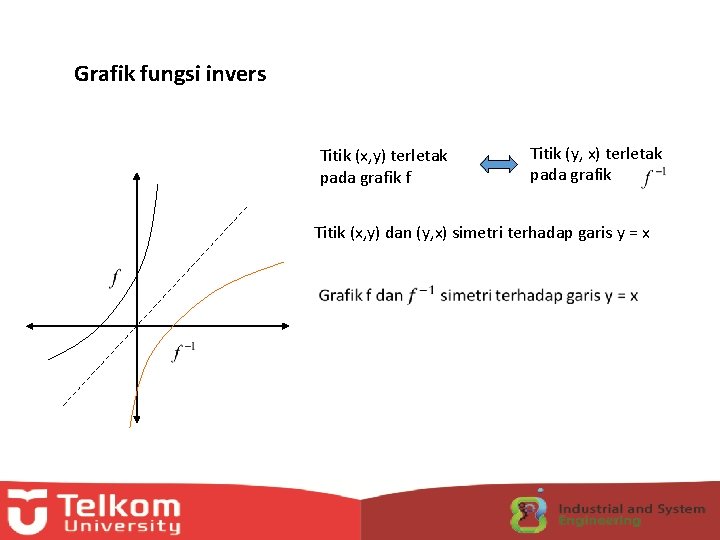
Grafik fungsi invers Titik (x, y) terletak pada grafik f Titik (y, x) terletak pada grafik Titik (x, y) dan (y, x) simetri terhadap garis y = x

Turunan fungsi invers Bentuk diatas dapat juga dituliskan sebagai Contoh 2: Diketahui . Tentukan Jawab : , y = 4 jika hanya jika x = 1

8. 2 Fungsi Logaritma Asli • Fungsi Logaritma asli ( ln ) didefinisikan sebagai : • Dengan Teorema Dasar Kalkulus II, diperoleh : . • Secara umum, jika u = u(x) maka

Contoh 3: Diberikan maka Jika Jadi, Dari sini diperoleh :

Sifat-sifat Ln : 1. ln 1 = 0 2. ln(ab) = ln a + ln b 3. ln(a/b)=ln(a) – ln(b) 4. ln ar = r ln a

Contoh 4: Hitung Jawab: Misal sehingga

Grafik fungsi logaritma asli Diketahui a. f(x) = lnx b. f selalu monoton naik pada Df 1 c. Grafik selalu cekung kebawah d. f(1) = 0

8. 3 Fungsi Eksponen Asli • Karena maka fungsi logaritma asli monoton murni, sehingga mempunyai invers. Invers dari fungsi logaritma asli disebut fungsi eksponen asli, notasi exp. Jadi berlaku hubungan • Dari sini didapat : y = exp (ln y) dan x = ln (exp (x)) • Definisi 8. 2 Bilangan e adalah bilangan real positif yang bersifat ln e = 1. Dari sifat (iv) fungsi logaritma diperoleh

Turunan dan integral fungsi eksponen asli Dengan menggunakan turunan fungsi invers Dari hubungan Secara umum Sehingga

Contoh 5 : Hitung Jawab : Misalkan Sehingga Contoh 6:

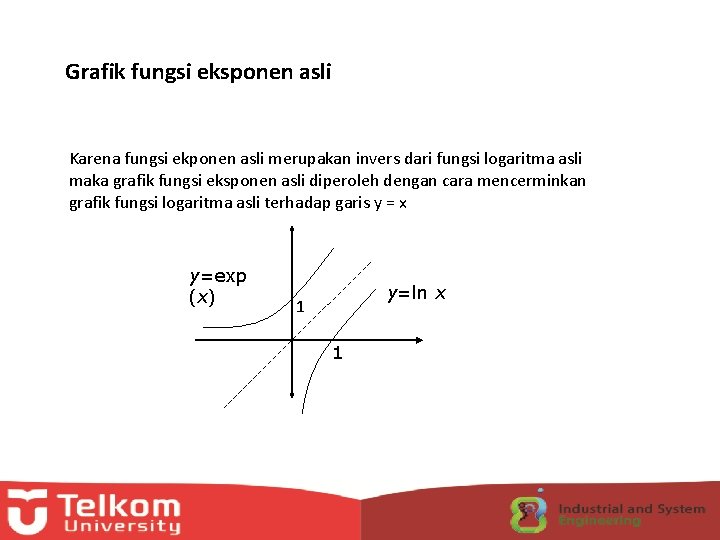
Grafik fungsi eksponen asli Karena fungsi ekponen asli merupakan invers dari fungsi logaritma asli maka grafik fungsi eksponen asli diperoleh dengan cara mencerminkan grafik fungsi logaritma asli terhadap garis y = x y=exp (x) y=ln x 1 1

Penggunaan fungsi logaritma dan eksponen asli Menghitung turunan fungsi berpangkat fungsi Diketahui Ingat!!!

Contoh 7: Tentukan turunan fungsi Jawab: Ubah bentuk fungsi pangkat fungsi menjadi perkalian fungsi dengan menggunakan fungsi logaritma asli Turunkan kedua ruas

Soal Latihan A. Periksa apakah fungsi-fungsi berikut memiliki invers! Jika ada, tentukan fungsi inversnya! 1. 2. 3. 4. 5. 6.

B. Tentukan dari : 1. 6. 2. 7. 3. 4. 5. 8. 9. 10.

C. Selesaikan integral tak tentu berikut 1. 2. 3. 4. 5.

D. Selesaikan integral tentu berikut 1. 2. 3. 4. 5.

8. 4 Fungsi Eksponen Umum Fungsi , a > 0 disebut fungsi eksponen umum Untuk a > 0 dan x R, definisikan Turunan dan integral Jika u = u(x), maka Dari sini diperoleh : :

Sifat–sifat fungsi eksponen umum Untuk a > 0, b > 0, x, y bilangan riil berlaku 1. 2. 3. 4. 5.

Contoh 8: 1. Hitung turunan pertama dari Jawab : 2. Hitung Jawab : Misal

Grafik fungsi eksponen umum Diketahui a. b. f monoton naik jika a > 1 f monoton turun jika 0 < a < 1 c. Grafik f selalu cekung keatas d. f(0) = 1

8. 5 Fungsi Logaritma Umum Karena fungsi eksponen umum monoton murni, maka ada inversnya. Invers dari fungsi eksponen umum disebut fungsi Logaritma Umum ( logaritma dengan bilangan pokok a ), notasi , sehingga berlaku : Dari hubungan ini, didapat Sehingga Jika u = u(x), maka

Contoh 9: Tentukan turunan pertama dari 1. 2. Jawab : 1. 2.

Grafik fungsi logaritma umum diperoleh dengan mencerminkan grafik fungsi eksponen umum terhadap garis y=x Untuk a > 1 Untuk 0 < a < 1

Soal Latihan A. Tentukan dari 1. 3. 2. 4. B. Hitung 5. 6. 7. 8.

8. 6 FUNGSI INVERS TRIGONOMETRI Fungsi trigonometri adalah fungsi yang periodik sehingga tidak satu-satu. Jika daerah asalnya dibatasi, fungsi trigonometri bisa dibuat menjadi satu-satu sehingga mempunyai invers. a. Invers fungsi sinus Diketahui f(x) = sinx , Karena pada , f(x)=sinx monoton murni maka inversnya ada. Invers dari fungsi sinus disebut arcus sinus, notasi arcsin(x) atau Sehingga berlaku

Turunan Dari hubungan dan rumus turunan fungsi invers diperoleh atau Jika u = u(x), Dari rumus turunan diperoleh Dengan cara yang sama diperoleh turunan fungsi invers trigonometri yang lain. Secara ringkas perhatikan tabel berikut:

Ge. NERALIzation

Gunakan formula Contoh 10: Hitung Jawab : Misal

Contoh 11:

Misal

Soal Latihan A. Tentukan turunan pertama fungsi berikut, sederhanakan jika mungkin 1. 2. 3. 4. 5. 6.

B. Hitung 1. 2. 3. 4.