MATHMATIQUES FINANCIRES I Vingtdeuxime cours 221107 Rappel du

MATHÉMATIQUES FINANCIÈRES I Vingt-deuxième cours 22/11/07

Rappel du dernier cours • Table d’amortissement dans le cas où les paiements sont égaux et les périodes de capitalisation et de paiement ne coïncident pas 22/11/07

Rappel du dernier cours • Table d’amortissement dans le cas où les paiements sont égaux et les périodes de capitalisation et de paiement ne coïncident pas • Fonds d’amortissement 22/11/07

Rappel du dernier cours • Table d’amortissement dans le cas où les paiements sont égaux et les périodes de capitalisation et de paiement ne coïncident pas • Fonds d’amortissement • Montant net du prêt 22/11/07

Rappel du dernier cours • Table d’amortissement dans le cas où les paiements sont égaux et les périodes de capitalisation et de paiement ne coïncident pas • Fonds d’amortissement • Montant net du prêt • Montant net d’intérêt payé 22/11/07

Rappel: Pour un prêt remboursé par n paiements égaux pour lequel les périodes de capitalisation de l’intérêt et de paiement ne coïncident pas. Il suffit de revenir au principe de base. Deux options s’offrent à nous, soit de convertir le taux d’intérêt à un dont la période de capitalisation est la période de paiement, soit de développer la théorie. 22/11/07

Rappel: Pour un prêt remboursé par n paiements égaux au montant de 1$ à la fin de chaque période de paiement. Supposons qu’il y a k périodes de capitalisation dans une période de paiement. Notons par i: le taux d’intérêt du prêt par période de capitalisation et par n: la durée du prêt en période de capitalisation. Le montant emprunté L est alors 22/11/07

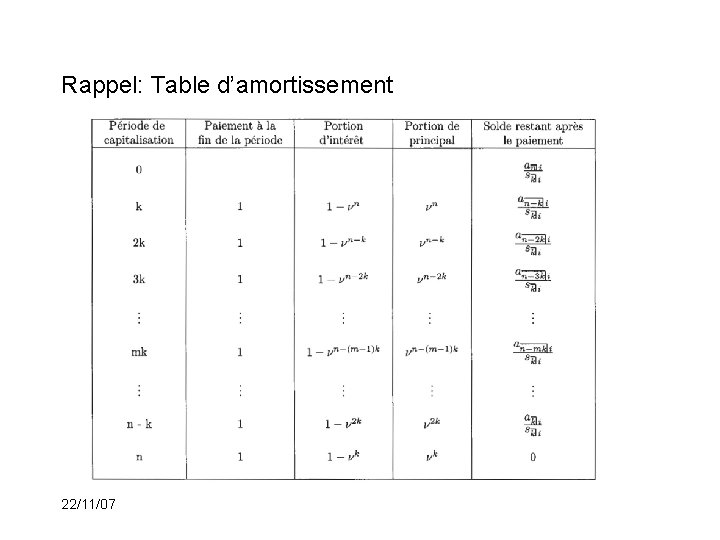
Rappel: Table d’amortissement 22/11/07

Rappel: Pour un prêt remboursé par des paiements égaux. Supposons qu’il y a m périodes de paiement dans une période de capitalisation. Notons par i: le taux d’intérêt du prêt par période de capitalisation et par n: la durée du prêt en période de capitalisation. Les paiements du prêt sont de (1/m) dollars et il y a mn paiements. Le montant emprunté L est alors 22/11/07

Rappel: Table d’amortissement 22/11/07

Rappel: Dans certains prêts, l’emprunteur verse à intervalles réguliers l’intérêt dû et remboursera complètement le principal L à l’échéance du prêt. Pour accumuler le montant du prêt à l’échéance, l’emprunteur met en place un fonds dans lequel il dépose à intervalles réguliers des versements de façon telle qu’il accumulera le principal L. Ce fonds est le fonds d’accumulation ( « sinking fund » ). 22/11/07

Rappel: Le montant accumulé dans le fonds peut à tout moment servir à rembourser une partie du prêt. Conséquemment le montant net du prêt est le principal prêté initialement auquel nous soustrayons la valeur accumulée dans le fonds. 22/11/07

Rappel: Le montant net d’intérêt payé pendant une période est le montant d’intérêt, auquel nous soustrayons l’intérêt gagné par le fonds peut à tout moment servir à rembourser une partie du prêt. 22/11/07

Rappel: Considérons un prêt de 1$, qui sera remboursé par un paiement de 1$ après n périodes de capitalisation. Le taux d’intérêt est le taux i par période de capitalisation. L’intérêt est payé à la fin de chaque période de capitalisation. Au même moment, un dépôt est fait dans un fonds rémunéré au taux d’intérêt j. Ces dépôts sont tous égaux et la valeur accumulée est 1$ après n périodes de capitalisation. La période de capitalisation de l’intérêt du fonds est la même que celle du prêt. Nous obtenons le tableau suivant. 22/11/07

Rappel: La table du fonds est 22/11/07

Nous aimerions déterminer le montant total versé (intérêt et dépôt dans le fonds d’amortissement) par l’emprunteur à partir du montant emprunté. 22/11/07

Notons par la valeur actuelle d’une annuité consistant en des paiements de 1$ à la fin de chaque période pour n périodes telle que est le montant d’intérêt payé sur le prêt et est le montant versé dans un fonds à chaque période. 22/11/07

Nous obtenons alors l’équation suivante: Conséquemment 22/11/07

Exemple 1: Reprenons l’exemple 4 du 21 e cours. Un prêt de 75 000$ est remboursé par un versement de 75 000$ après huit ans et des versements annuels d’intérêt faits à la fin de chaque année pendant 8 ans. Le taux d’intérêt est le taux effectif d’intérêt i = 5% par année. Ainsi l’emprunteur paiera 3750$ d’intérêt par année. Un fonds d’amortissement est mis en place pour accumuler le 75 000$ à la fin de la huitième année. Ce fonds est rémunéré au taux effectif d’intérêt j = 3% par année. Des dépôts de 8434. 23 dollars seront faits à la fin de chaque année pendant 8 ans. Ainsi à chaque année, l’emprunteur versera 12 184. 23$ correspondant à l’intérêt sur le prêt et au dépôt dans le fonds. 22/11/07

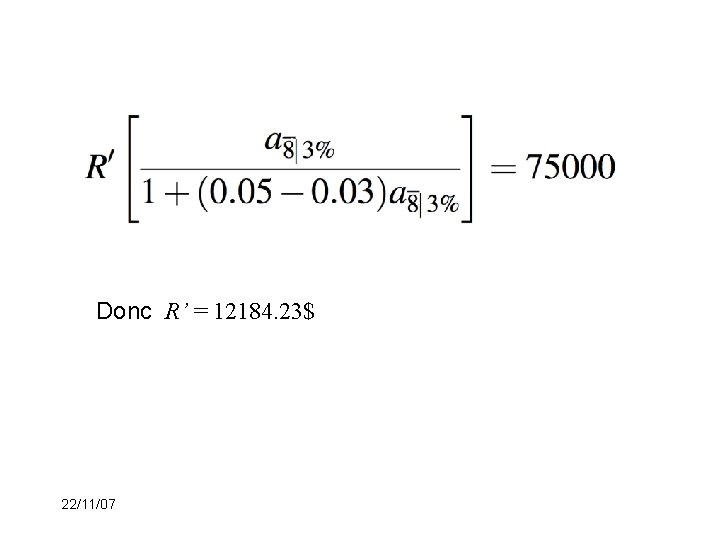
Exemple 1: (suite) Si nous utilisons maintenant ce que nous venons de développer et que nous notons par R’: le montant total à verser par l’emprunteur à chaque année pour l’intérêt à payeer et le dépôt, alors nous avons l’équation de valeur Nous obtenons alors 22/11/07

Donc R’ = 12184. 23$ 22/11/07

Dans le cas où le taux d’intérêt du prêt i est égale au taux d’intérêt du fonds d’amortissement j, alors la table d’amortissement du prêt est équivalente à celle du fonds d’amortissement lorsque les paiements sont égaux pour la table d’amortissement et les dépôts dans le fonds d’amortissement sont égaux. Nous avons les égalités suivantes: 22/11/07

Le montant net d’intérêt payé à e la fin de la k période dans le cas du fonds d’amortissement est égal à la portion d’intérêt payé dans le ke paiement dans la table d’amortissement. 22/11/07

Le montant net du prêt après le e k dépôt dans le cas du fonds d’amortissement est égal au solde restant après le ke paiement dans la table d’amortissement. 22/11/07

Si i = j, nous avons aussi que et le total versé (intérêt et dépôt) dans le cas du fonds d’amortissement est égal au paiement dans le cas de la table d’amortissement. 22/11/07

Nous pouvons maintenant expliquer la formule À droite, il s’agit du total versé (intérêt et dépôt) dans le cas du fonds d’amortissement et, à gauche, du paiement dans le cas de la table d’amortissement. 22/11/07

Nous allons maintenant illustrer cette équivalence entre la table d’amortissementd’un prêt et celle d’un fonds d’amortissement lorsque i = j. 22/11/07

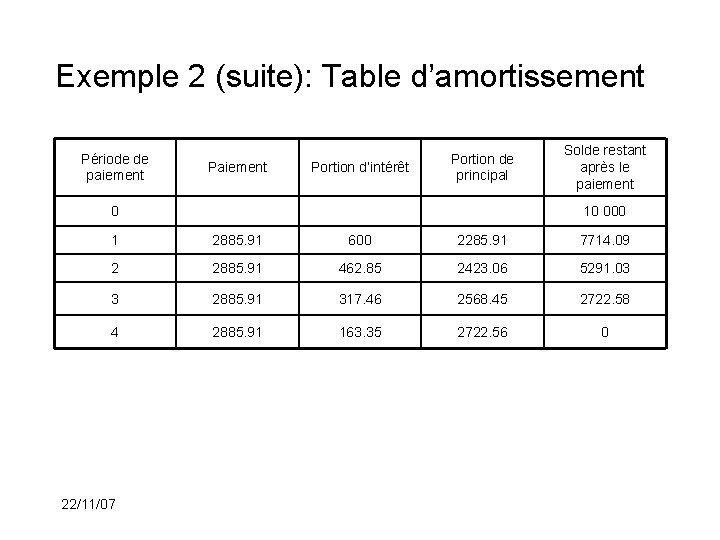
Exemple 2: Considérons un prêt de 10 000$ remboursé par 4 versement égaux à la fin de chaque année, le premier versement étant fait un an après le prêt. Le taux d’intérêt est le taux effectif d’intérêt i = 6% par année. Ainsi l’emprunteur paiera 2885. 91$ par année. La table d’amortissement est 22/11/07

Exemple 2 (suite): Table d’amortissement Période de paiement Portion d’intérêt Portion de principal 0 Solde restant après le paiement 10 000 1 2885. 91 600 2285. 91 7714. 09 2 2885. 91 462. 85 2423. 06 5291. 03 3 2885. 91 317. 46 2568. 45 2722. 58 4 2885. 91 163. 35 2722. 56 0 22/11/07

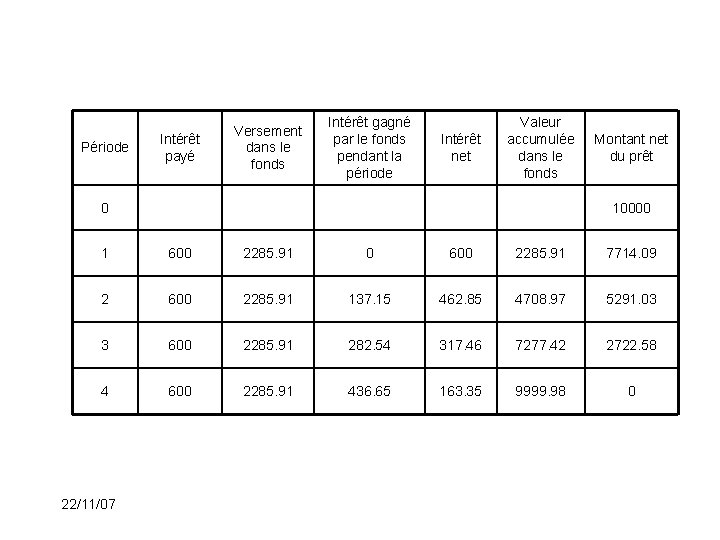
Exemple 2: (suite) Considérons maintenant un prêt de 10 000$ remboursé par un versement de 10000$ à la fin de la quatrième année. À la fin de chaque année, l’intérêt dû est payé au taux d’intérêt de i = 6% par année, à savoir 600$ sont payés. Au même moment, des dépôts de 2285. 91$ sont faits dans un fonds d’amortissement. Ce dernier est rémunéré au taux effectif d’intérêt i = 6% par année. Ainsi l’emprunteur paiera au total 2885. 91$ par année. La table de ce fonds est 22/11/07

Période Intérêt payé Versement dans le fonds Intérêt gagné par le fonds pendant la période Intérêt net Valeur accumulée dans le fonds 0 Montant net du prêt 10000 1 600 2285. 91 0 600 2285. 91 7714. 09 2 600 2285. 91 137. 15 462. 85 4708. 97 5291. 03 3 600 2285. 91 282. 54 317. 46 7277. 42 2722. 58 4 600 2285. 91 436. 65 163. 35 9999. 98 0 22/11/07

Exemple 3: Un prêt de 5 000$ est remboursé par un versement de 5 000$ après dix ans et des versements annuels d’intérêt faits à la fin de chaque année pendant 10 ans. Le taux d’intérêt est le taux effectif d’intérêt i = 4% par année. Ainsi l’emprunteur paiera 5 000 (0. 04) = 200 000$ d’intérêt par année. Un fonds d’amortissement est mis en place pour accumuler le 5 000$ à la fin de la dixième année. Ce fonds est rémunéré au taux effectif d’intérêt j = 3% par année. Les dépôts seront faits à la fin de chaque année pendant 10 ans, le premier est de R dollars et les paiements subséquents augmenteront de 5% avec chaque année. Déterminons le montant net du prêt après le 6 e année, ainsi que le montant net d’intérêt payé à la fin de la 8 e année. 22/11/07

Exemple 3: (suite) Déterminons premièrement R. Les dépôts dans le fonds forme une suite géométrique et nous avons alors et nous obtenons alors que R = 350 903. 98$ 22/11/07

Exemple 3: (suite) Le montant net du prêt est le montant emprunté, i. e. 5 000$, auquel nous soustrayons le montant accumulé dans le fonds d’amortissement. Donc le montant net du prêt à la fin de la 6 e année est 22/11/07

Exemple 3: (suite) Le montant net d’intérêt payé est le montant d’intérêt , i. e. 200 000$, auquel nous soustrayons le montant d’intérêt gagné par le fonds d’amortissement pendant la période. Donc le montant net d’intérêt payé à la fin de la 8 e année est 22/11/07

CHAPITRE VII Obligations 22/11/07

Une obligation est un titre rapportant de l’intérêt et dans lequel l’emprunteur, appelé l’émetteur, s’engage à verser un montant déterminé à une date future aux prêteurs, appelés les souscripteurs. Les obligations d’épargne sont des obligations de capitalisation ou d’accumulation. L’emprunteur rembourse le principal et les intérêts à l’échéance ou parfois au moment où le souscripteur veut être remboursé. 22/11/07

Nous allons maintenant décrire ce qu’est une obligation négociable. L’émetteur s’engage à verser de l’intérêt à intervalles réguliers et à rembourser un montant déterminé à une date future aux souscripteurs. Celles-ci sont émises dans un marché primaire et ensuite sont transigées sur un marché secondaire. Un investisseur peut acheter ou vendre des obligations via son courtier sur le marché secondaire. 22/11/07

Ces obligation sont souvent dites obligations avec coupon. L’émetteur s’engage à verser aux souscripteurs l’intérêt à intervalles réguliers (ce sont les coupons) et la valeur de remboursement de l’obligation à une date d’échéance déterminée. 22/11/07

Nous voulons maintenant relier le prix de l’obligation à son taux de rendement. Il nous faut donc fixer quelques notations. 22/11/07

Notation: • P désignera le prix de l’obligation. C’est ce que paie le souscripteur • F désignera la valeur nominale de l’obligation ( « face amount » ou « par value » en anglais). Il s’agit de la valeur inscrite sur l’obligation et qui sert à déterminer le montant d’intérêt à verser régulièrement. • C désignera la valeur de remboursement, i. e. le montant remboursé à l’échéance. En général, C = F et nous disons que l’obligation est remboursé au pair. Il peut arriver que C ≠ F. 22/11/07

Notation: (suite) • r est le taux d’intérêt par période de capitalisation de l’intérêt (ou encore par période de paiement des coupons). C’est le taux facial. Il est indiqué sur l’obligation et sert à déterminer le montant d’intérêt que l’émetteur doit verser régulièrement aux souscripteurs. Ce peut être un taux nominal. En Amérique du Nord, ce taux est souvent un taux nominal capitalisé semestriellement, alors qu’en Europe il s’agit plutôt d’un taux effectif. • Fr est le montant d’intérêt versé périodiquement. Ce montant est appelé le coupon. 22/11/07

Notation: (suite) • g est le taux modifié d’intérêt par période de capitalisation de l’intérêt (ou encore par période de paiement des coupons). g est défini par l’équation Cg = Fr. Si l’obligation est remboursé au pair, alors g = r. • i désignera le taux de rendement de l’obligation par période de paiement des coupons en supposant que l’obligation est détenue jusqu’à sa date de maturité ou de rédemption et que les versements de l’intérêt (i. e. les coupons) sont réinvestis aussi au taux i. En général, ce taux est exprimé comme un taux nominal pour lequel la période de capitalisation est celle des coupons. 22/11/07

Notation: (suite) • n est le durée de vie de l’obligation, i. e. le nombre de périodes de capitalisation du taux de rendement jusqu’à la date de maturité ou de rédemption de l’obligation. Nous supposerons premièrement que n est bien déterminé. Nous discuterons plus tard le cas des obligations rachetables ( « callable bonds » ). Dans ce dernier cas, il y a des dates possibles de rachat par l’émetteur de l’obligation. Ceci aura aussi des incidences sur le taux de rendement. • K désignera la valeur actuelle de la valeur de remboursement C de l’obligation à la date de maturité ou de rédemption calculée au taux de rendement i, c’est-à-dire K = C n où = (1 + i)-1. • G est le montant de base de l’obligation, i. e. le montant qui investit au taux de rendement i engendre les mêmes coupons. Donc G est défini par Gi = Fr. 22/11/07

Pour une obligation, F, C, r et n sont fixés. Le prix P et le taux de rendement i varient selon les conditions du marché. Intuitivement si P augmente, alors i diminue et inversement si P diminue, alors i augmente. 22/11/07

La formule basique reliant le prix P et le taux de rendement i immédiatement après le paiement d’un coupon est ou encore 22/11/07