MATHMATIQUES FINANCIRES I Douzime cours ACT 2025 Cours

MATHÉMATIQUES FINANCIÈRES I Douzième cours ACT 2025 - Cours 12

Rappel: • Détermination du taux d’intérêt étant donné la valeur accumulée, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période ACT 2025 - Cours 12

Rappel: • Détermination du taux d’intérêt étant donné la valeur accumulée, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période • Détermination du taux d’intérêt dans le cas d’annuité de début de période ACT 2025 - Cours 12

Rappel: • Détermination du taux d’intérêt étant donné la valeur accumulée, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période • Détermination du taux d’intérêt dans le cas d’annuité de début de période • Annuités générales ACT 2025 - Cours 12

Rappel: • Détermination du taux d’intérêt étant donné la valeur accumulée, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période • Détermination du taux d’intérêt dans le cas d’annuité de début de période • Annuités générales • Situation dans laquelle le taux d’intérêt varie avec les périodes de paiement ACT 2025 - Cours 12

Rappel: • Détermination du taux d’intérêt étant donné la valeur accumulée, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période • Détermination du taux d’intérêt dans le cas d’annuité de début de période • Annuités générales • Situation dans laquelle le taux d’intérêt varie avec les périodes de paiement • Situation dans laquelle le taux d’intérêt varie avec les paiements ACT 2025 - Cours 12

Rappel: • Détermination du taux d’intérêt étant donné la valeur accumulée, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période • Détermination du taux d’intérêt dans le cas d’annuité de début de période • Annuités générales • Situation dans laquelle le taux d’intérêt varie avec les périodes de paiement • Situation dans laquelle le taux d’intérêt varie avec les paiements • Situation dans laquelle les périodes de paiement et de capitalisation sont différentes ACT 2025 - Cours 12

Rappel: La méthode de Newton-Raphson pour déterminer le taux d’intérêt i numériquement dans l’équation alors que nous connaissons F, R et n nous donne ACT 2025 - Cours 12

Rappel: et comme valeur initiale ACT 2025 - Cours 12

Rappel: est équivalente à l’équation ACT 2025 - Cours 12

Rappel: est équivalente à l’équation ACT 2025 - Cours 12

Rappel: Les annuités générales seront celles pour lesquelles • soit le taux d’intérêt varie avec les périodes de paiement ACT 2025 - Cours 12

Rappel: Les annuités générales seront celles pour lesquelles • soit le taux d’intérêt varie avec les périodes de paiement • soit les périodes de paiement et de capitalisation sont différentes ACT 2025 - Cours 12

Rappel: Les annuités générales seront celles pour lesquelles • soit le taux d’intérêt varie avec les périodes de paiement • soit les périodes de paiement et de capitalisation sont différentes • soit que les paiements ne sont pas constants ACT 2025 - Cours 12

Rappel: Soit une annuité consistant en n paiements de 1$ à la fin de chaque période. Le taux d’intérêt pour la ke période est ik et s’applique à tous les paiements de l’annuité pendant cette période. Sa valeur actuelle est ACT 2025 - Cours 12

Rappel: Soit une annuité consistant en n paiements de 1$ à la fin de chaque période. Le taux d’intérêt pour la ke période est ik et s’applique à tous les paiements de l’annuité pendant cette période. Sa valeur actuelle est Sa valeur accumulée immédiatement après le dernier paiement est ACT 2025 - Cours 12

Rappel: Soit une annuité consistant en n paiements de 1$ à la fin de chaque période. Le taux d’intérêt ik est applicable au ke paiement et est le même pour ce paiement pour chaque période. Sa valeur actuelle est ACT 2025 - Cours 12

Rappel: Soit une annuité consistant en n paiements de 1$ à la fin de chaque période. Le taux d’intérêt ik est applicable au ke paiement et est le même pour ce paiement pour chaque période. Sa valeur actuelle est Sa valeur accumulée immédiatement après le dernier paiement est ACT 2025 - Cours 12

Rappel: Nous noterons ces valeurs actuelles et accumulées par analogie à ce que nous avons fait précédemment respectivement par et ACT 2025 - Cours 12

Rappel: Pour des annuités pour lesquelles périodes de paiement et de capitalisation de l’intérêt sont différentes, soit la période de paiement est plus courte que celle de capitalisation de l’intérêt, soit la période de paiement est plus longue que celle de capitalisation de l’intérêt. Comme première méthode, il suffit de convertir le taux d’intérêt à un taux équivalent. ACT 2025 - Cours 12

Exemple 1: Alex emprunte 10 000$ à la banque des. Nababs. Il remboursera ce prêt en faisant des paiements à la fin de chaque trimestre pendant 5 ans. Les versements pour les deux premières années sont de R dollars et pour les trois dernières années sont de 1. 5 R dollars. Le taux d’intérêt de ce prêt est le taux nominal i(12) = 9% par année capitalisé mensuellement. Déterminons R. ACT 2025 - Cours 12

Exemple 1: (suite) Si i(12) = 9%, alors le taux effectif d’intérêt équivalent est 9. 380689767% par année. De ceci, nous obtenons que le taux nominal i(4) = 9. 06766875% par année capitalisé trimestriellement est équivalent à i(12) = 9%. Conséquemment le taux d’intérêt par trimestre équivalent au taux i(12) = 9% est ACT 2025 - Cours 12

Exemple 1: (suite) Le diagramme d’entrées et sorties est le suivant: ACT 2025 - Cours 12

Exemple 1: (suite) L’équation de valeur à la date de comparaison t = 0 est alors ACT 2025 - Cours 12

Exemple 1: (suite) L’équation de valeur à la date de comparaison t = 0 est alors Nous obtenons alors R = 492. 95$. ACT 2025 - Cours 12

Exemple 2: Béatrice a accumulé 100000$. Elle utilise ce capital pour s’acheter une rente qui lui versera 1500$ par mois. Le premier versement de cette rente est fait un mois après son achat. Le taux d’intérêt est le taux effectif de i = 5% par année. Combien de versements recevra-t-elle si elle désire utiliser tout ce capital, que tous les versements soient de 1500$, à l’exception du dernier qui sera gonflé? ACT 2025 - Cours 12

Exemple 2: (suite) Si le taux effectif est i = 5%, alors le taux nominal d’intérêt i(12) équivalent est i(12) = 4. 888948519% par année. De ceci nous obtenons que le taux d’intérêt par mois équivalent à i est ACT 2025 - Cours 12

Exemple 2: (suite) Dans un premier temps, nous allons déterminer n + k, avec n entier et k compris entre 0 et 1, tel que ACT 2025 - Cours 12

Exemple 2: (suite) Nous obtenons ainsi que n + k = 77. 94593822. Ainsi n = 77 et k = 0. 94593822. La rente versera 76 versements de 1500$ et un dernier au montant de X dollars. ACT 2025 - Cours 12

Exemple 2: (suite) Nous obtenons ainsi que n + k = 77. 94593822. Ainsi n = 77 et k = 0. 94593822. La rente versera 76 versements de 1500$ et un dernier au montant de X dollars. Le diagramme d’entrées et sorties est ACT 2025 - Cours 12

Exemple 2: (suite) L’équation de valeur avec comme date de comparaison t = 0 est alors ACT 2025 - Cours 12

Exemple 2: (suite) L’équation de valeur avec comme date de comparaison t = 0 est alors Nous obtenons que X = 2913. 31$. Ainsi Béatrice recevra 76 versements mensuels de 1500$ et un dernier versement de 2913. 31$. ACT 2025 - Cours 12

Nous allons maintenant développer la seconde méthode. Il s’agit d’une approche théorique. Il faut distinguer les deux cas selon que la période de paiement est plus longue ou plus courte que la période de capitalisation. ACT 2025 - Cours 12

Nous allons maintenant considérer les annuités pour lesquelles la période de paiement est plus longue que celle de la capitalisation de l’intérêt. Nous supposerons qu’il y a k périodes de capitalisation de l’intérêt dans une période de paiement. L’exemple 1 est dans cette situation. ACT 2025 - Cours 12

Nous noterons le terme de l’annuité, c’est-à-dire sa durée, par n et celui-ci est mesuré en périodes de capitalisation. Le taux d’intérêt par période de capitalisation sera noté par i et (1 + i) est le facteur d’escompte. ACT 2025 - Cours 12

Il y aura (n/k) paiements parce qu’il y a k périodes de capitalisation dans une période de paiement. ACT 2025 - Cours 12

Considérons maintenant une annuité consistant en (n/k) paiements de 1$ faits à la fin de chacune des périodes de paiement. ACT 2025 - Cours 12

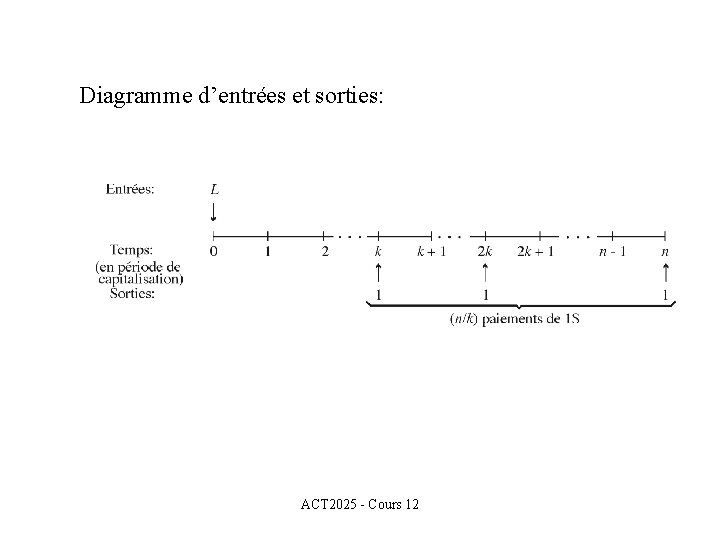
Nous allons maintenant déterminer la valeur actuelle de cette annuité. Nous noterons celle-ci par L dans le diagramme d’entrées et sorties suivant. ACT 2025 - Cours 12

Diagramme d’entrées et sorties: ACT 2025 - Cours 12

Algébriquement nous obtenons que cette valeur actuelle L est ACT 2025 - Cours 12

Algébriquement nous obtenons que cette valeur actuelle L est Il est aussi possible de donner une explication de cette formule en termes d’annuités. ACT 2025 - Cours 12

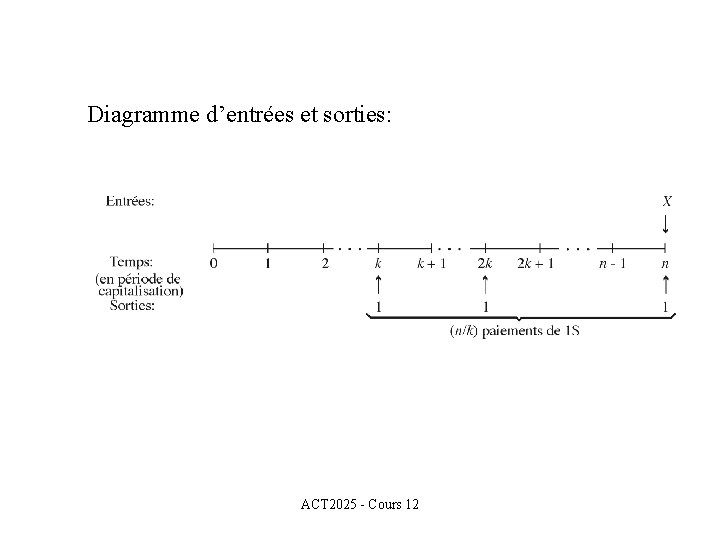
Nous allons maintenant déterminer la valeur accumulée de cette annuité au dernier versement. Nous noterons celle-ci par X dans le diagramme d’entrées et sorties suivant. ACT 2025 - Cours 12

Diagramme d’entrées et sorties: ACT 2025 - Cours 12

Algébriquement nous obtenons que cette valeur accumulée X est ACT 2025 - Cours 12

Algébriquement nous obtenons que cette valeur accumulée X est Il est aussi possible de donner une explication de cette formule en termes d’annuités. ACT 2025 - Cours 12

Exemple 3: Carole a emprunté 20 000$ qu’elle remboursera en faisant 36 paiements trimestriels égaux, le premier étant fait 3 mois après le prêt. Le taux d’intérêt de ce prêt est le taux nominal d ’intérêt i(12) = 9% par année capitalisé mensuellement. Notons par R: le montant de ces paiements trimestriels. Nous voulons déterminer R. ACT 2025 - Cours 12

Exemple 3: (suite) Carole a emprunté 20 000$ qu’elle remboursera en faisant 36 paiements trimestriels égaux, le premier étant fait 3 mois après le prêt. Le taux d’intérêt de ce prêt est le taux nominal d ’intérêt i(12) = 9% par année capitalisé mensuellement. Notons par R: le montant de ces paiements trimestriels. Nous voulons déterminer R. Dans cette situation k = 3, n = 36 x 3 = 108 périodes de capitalisation et i = 9%/12 = 0. 75%. ACT 2025 - Cours 12

Exemple 3: (suite) L’équation de valeur avec comme date de comparaison t = 0 est ACT 2025 - Cours 12

Exemple 3: (suite) L’équation de valeur avec comme date de comparaison t = 0 est Nous obtenons ainsi que R = 818. 68$. ACT 2025 - Cours 12

Exemple 3: (suite) Si nous avions utilisé la première méthode, il nous faudrait calculer le taux d’intérêt par trimestre équivalent au taux nominal i(12) = 9%. Nous obtenons ainsi le taux effectif équivalent au taux nominal i(12) = 9% est 9. 380689764% et conséquemment le taux nominal i(4) équivalent à i(12) = 9% est i(4) = 9. 06766874%. Donc le taux par trimestre équivalent au taux i(12) est 2. 266917185%. ACT 2025 - Cours 12

Exemple 3: (suite) Conséquemment l’équation de valeurs à la date de comparaison t = 0 est Nous obtenons là aussi que R = 818. 68$. ACT 2025 - Cours 12

Exemple 4: Dora dépose 20 000$ tous les ans pendant 10 ans. Les dépôts sont faits à la fin de l’année. Le taux d’intérêt de ce placement est le taux nominal i(365) = 3. 65% par année capitalisé quotidiennement. Nous voulons déterminer le montant accumulé à la fin de la dixième année. ACT 2025 - Cours 12

Exemple 4: (suite) Dora dépose 20 000$ tous les ans pendant 10 ans. Les dépôts sont faits à la fin de l’année. Le taux d’intérêt de ce placement est le taux nominal i(365) = 3. 65% par année capitalisé quotidiennement. Nous voulons déterminer le montant accumulé à la fin de la dixième année. Dans cette situation k = 365, n = 10 x 365 = 3650 périodes de capitalisation et i = 3. 65%/365 = 0. 01%. ACT 2025 - Cours 12

Exemple 4: (suite) La valeur accumulée recherchée est ACT 2025 - Cours 12

Exemple 4: (suite) Si nous avions utilisé la première méthode, il nous faudrait calculer le taux effectif d’intérêt par année équivalent au taux nominal i(365) = 3. 65%. Nous obtenons ainsi que ce taux effectif équivalent au taux nominal i(365) = 3. 65% est 3. 717241117%. Donc la valeur accumulée recherchée est ACT 2025 - Cours 12

Exemple 5: Reprenons l’exemple 1, mais avec cette autre approche. Alex emprunte 10000$ à la banque des. Nababs. Il rembourse ce prêt en faisant des paiements à la fin de chaque trimestre pendant 5 ans. Les versements pour les deux premières années sont de R dollars et pour les trois dernières années sont de 1. 5 R dollars. Le taux d’intérêt de ce prêt est le taux nominal i(12) = 9% par année capitalisé mensuellement. ACT 2025 - Cours 12

Exemple 5: (suite) Il s’agit d’une annuité ayant 8 paiements de R dollars et d’une annuité différée ayant 12 paiements de 1. 5 R dollars. Nous allons calculer la valeur actuelle (à t = 0) de chacune des annuités. Dans les deux cas, le taux d’intérêt par mois est (i(12)/12) = (9%/12) = 0. 75%. ACT 2025 - Cours 12

Exemple 5: (suite) Pour la première annuité, celle ayant 8 paiements trimestriels au montant de R dollars, alors k = 3 et n = 8 x 3 = 24. Sa valeur actuelle est ACT 2025 - Cours 12

Exemple 5: (suite) Pour la deuxième annuité, celle ayant 12 paiements trimestriels au montant de 1. 5 R dollars, alors k = 3 et n = 12 x 3 = 36. Sa valeur actuelle est ACT 2025 - Cours 12

Exemple 5: (suite) L’équation de valeur à t = 0 est alors ACT 2025 - Cours 12

Exemple 5: (suite) L’équation de valeur à t = 0 est alors Nous obtenons alors que R = 492. 95$. ACT 2025 - Cours 12

Exemple 5: (suite) Noter que pour la seconde annuité il faut escompter de 24 périodes de capitalisation, c’est-à-dire 8 périodes de paiement, la valeur pour obtenir la valeur à t = 0. ACT 2025 - Cours 12