MATHMATIQUES FINANCIRES I Onzime cours ACT 2025 Cours

MATHÉMATIQUES FINANCIÈRES I Onzième cours ACT 2025 - Cours 11

Rappel: • Méthode de Newton-Raphson ACT 2025 - Cours 11

Rappel: • Méthode de Newton-Raphson • Détermination du taux d’intérêt étant donné la valeur actuelle, le nombre de paiement et le montant des paiements d’une annuité simple constante de fin de période ACT 2025 - Cours 11

Rappel: Pour la méthode de Newton-Raphson, il nous faut un valeur initiale x 0 et utiliser la règle récursive pour construire une suite x 1, x 2, …, xs, … qui converge vers un zéro de f(x) (si les conditions sont bonnes) ACT 2025 - Cours 11

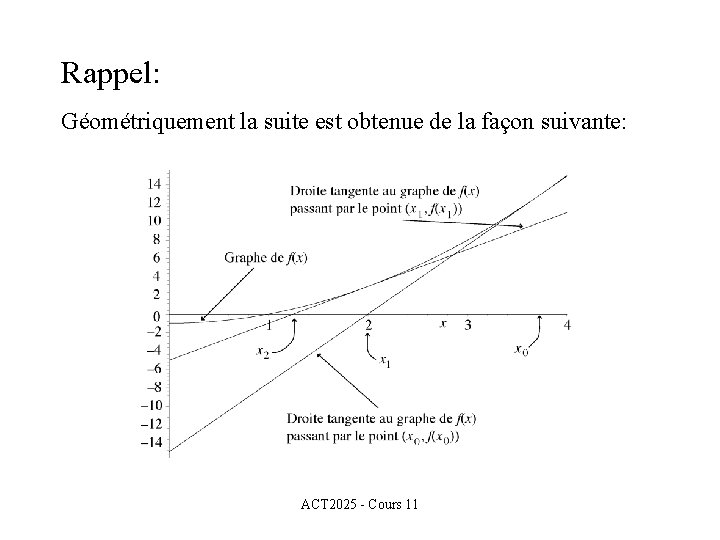
Rappel: Géométriquement la suite est obtenue de la façon suivante: ACT 2025 - Cours 11

Rappel: La méthode de Newton-Raphson pour déterminer le taux d’intérêt i numériquement dans l’équation alors que nous connaissons L, R et n nous donne ACT 2025 - Cours 11

Rappel: et comme valeur initiale ACT 2025 - Cours 11

Nous voulons résoudre maintenant l’équation alors que nous connaissons F, R et n. Nous voulons déterminer i. Ceci est équivalent à résoudre l’équation: ACT 2025 - Cours 11

Nous cherchons à déterminer un zéro de la fonction ACT 2025 - Cours 11

La règle récursive de la méthode de Newton-Raphson est alors ACT 2025 - Cours 11

Pour compléter la méthode de Newton-Raphson, il nous faut une valeur initiale i 0 près de la valeur recherchée i. Une bonne approximation est obtenue en considérant comme valeur initiale ACT 2025 - Cours 11

Nous allons maintenant justifier notre choix de valeur initiale i 0 : Nous allons ainsi faire deux hypothèses simplificatrices pour obtenir cette première approximation. ACT 2025 - Cours 11

Première hypothèse: Nous pouvons remplacer les n paiements de R dollars par un seul paiement de n. R dollars. Idéalement pour obtenir une situation équivalente à celle des n paiements, nous ferions ce paiement à l’échéance moyenne. Faute de connaître le taux d’intérêt i, nous allons utiliser l’échéance moyenne approchée. ACT 2025 - Cours 11

Deuxième hypothèse: Nous allons approximer l’intérêt en calculant plutôt le taux d’escompte d et en supposant qu’il s’agit d’escompte simple. Nous allons approximer le taux d’intérêt i recherché en prenant comme première valeur i 0 : ce taux d’escompte d. ACT 2025 - Cours 11

Justification heuristique de l’approximation: L’échéance moyenne approchée est car ACT 2025 - Cours 11

Justification heuristique: (suite) Nous pouvons considérer notre transaction comme une sortie au montant de F dollars au temps t = n et une entrée de n. R dollars au temps t = (n + 1)/2. ACT 2025 - Cours 11

Justification heuristique: (suite) Nous notons par d: l’approximation lors que nous considérons le flux précédent et que nous supposons de l’escompte simple. Nous obtenons alors l’équation: ACT 2025 - Cours 11

Justification heuristique: (suite) Nous obtenons ainsi facilement que Ceci est notre choix de i 0 ACT 2025 - Cours 11

Justification heuristique: (suite) Il est aussi possible d’obtenir une justification plus mathématique, justification qui fait appel à la série binomiale. Ceci est présenté dans le recueil de notes de cours. ACT 2025 - Cours 11

Exemple 1: Supposons que nous versons à tous les fins de mois 350$ pendant 6 ans dans un placement rémunéré au taux nominal d’intérêt i(12) par année capitalisé mensuellement. Immédiatement après le dernier versement, le montant accumulé est égal à 30000$. Déterminons i(12) approximativement au moyen de la méthode de Newton. Raphson. ACT 2025 - Cours 11

Exemple 1: (suite) Nous avons ainsi que F = 30 000, R = 350, n = 6 x 12 = 72 et notons le taux d’intérêt par mois par i. ACT 2025 - Cours 11

Exemple 1: (suite) La valeur initiale que nous pouvons utiliser pour la méthode de Newton-Raphson est alors ACT 2025 - Cours 11

Exemple 1: (suite) La règle récursive pour la méthode de Newton-Raphson est alors ACT 2025 - Cours 11

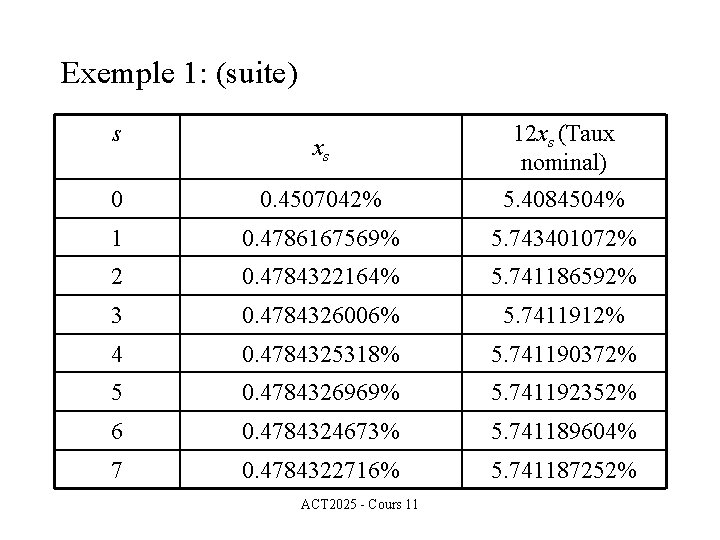
Exemple 1: (suite) En utilisant cette règle et cette valeur initiale, nous pouvons approximer le taux d’intérêt par mois et en multipliant par 12 ces taux obtenir une approximation du taux nominal recherché. Nous avons présenté ces valeurs dans le tableau suivant. ACT 2025 - Cours 11

Exemple 1: (suite) s xs 12 xs (Taux nominal) 0 0. 4507042% 5. 4084504% 1 0. 4786167569% 5. 743401072% 2 0. 4784322164% 5. 741186592% 3 0. 4784326006% 5. 7411912% 4 0. 4784325318% 5. 741190372% 5 0. 4784326969% 5. 741192352% 6 0. 4784324673% 5. 741189604% 7 0. 4784322716% 5. 741187252% ACT 2025 - Cours 11

Exemple 1: (suite) Le taux nominal recherché est approximativement 5. 74118% ACT 2025 - Cours 11

Nous avons traité que du cas des annuités de fin de période. Bien entendu les mêmes techniques peuvent être utilisées dans le cas des annuités de début de période. Cependant pour résoudre ces équations impliquant des annuités de début de période, il est plus simple de les convertir en annuités de fin de période. ACT 2025 - Cours 11

Ainsi l’équation est équivalente à l’équation Nous savons traiter cette dernière équation. ACT 2025 - Cours 11

Alors que l’équation est équivalente à l’équation Nous savons traiter cette dernière équation. ACT 2025 - Cours 11

CHAPITRE IV Annuités générales ACT 2025 - Cours 11

Jusqu’à maintenant nous avons traité que d’annuités simples constantes et pour lesquelles périodes de paiement et de capitalisation sont les mêmes. Il nous faut considérer des situations plus générales. ACT 2025 - Cours 11

Nous allons donc considérer des annuités pour lesquelles • soit le taux d’intérêt varie avec les périodes de paiement ACT 2025 - Cours 11

Nous allons donc considérer des annuités pour lesquelles • soit le taux d’intérêt varie avec les périodes de paiement • soit les périodes de paiement et de capitalisation sont différentes ACT 2025 - Cours 11

Nous allons donc considérer des annuités pour lesquelles • soit le taux d’intérêt varie avec les périodes de paiement • soit les périodes de paiement et de capitalisation sont différentes • soit que les paiements ne sont pas constants ACT 2025 - Cours 11

Nous allons maintenant considérer ce qui se passe lorsque le taux d’intérêt varie avec les périodes de paiement • soit le taux d’intérêt pour la ke période est ik et s’applique à tous les paiements pendant cette période ACT 2025 - Cours 11

Nous allons maintenant considérer ce qui se passe lorsque le taux d’intérêt varie avec les périodes de paiement • soit le taux d’intérêt pour la ke période est ik et s’applique à tous les paiements pendant cette période • soit le taux d’intérêt est applicable au ke paiement et pour ce paiement, il est le même pour chaque période ACT 2025 - Cours 11

Considérons la situation d’une annuité pour laquelle le taux d’intérêt pour la ke période est ik et s’applique à tous les paiements de l’annuité pendant cette période. ACT 2025 - Cours 11

Si nous considérons une annuité consistant en n paiements de 1$ à la fin de chaque période, alors nous obtenons que sa valeur actuelle est Par analogie, nous noterons ceci par ACT 2025 - Cours 11

Pour la même annuité, nous obtenons que la valeur accumulée immédiatement après le dernier paiement est Par analogie, nous noterons ceci par ACT 2025 - Cours 11

Exemple 2: Supposons que, pour un prêt, le taux d’intérêt est 4% pour la première année, 4. 5% pour la deuxième année, 5% pour la troisième année, 5% pour la quatrième année et 4. 5% pour la cinquième année. 10000$ est emprunté et ce prêt est remboursé par des paiements de R dollars à la fin de chaque année pendant 5 ans. Déterminons R. ACT 2025 - Cours 11

Exemple 2: (suite) Nous avons ainsi l’équation R (1. 04)-1 + R(1. 04)-1(1. 045)-1(1. 05)-1 + R (1. 04)-1(1. 045)-1(1. 05)-2 + R (1. 04)-1(1. 045)-2(1. 05)-1 || 10000. Nous obtenons alors que R = 2277. 27$ ACT 2025 - Cours 11

Exemple 3: Supposons que nous plaçons 1000$ au début de chaque année. Si le taux d’intérêt est 4% pour la première année, 4. 5% pour la deuxième année, 5% pour la troisième année, 5% pour la quatrième année et 4. 5% pour la cinquième année. Déterminons le montant accumulé à la fin de la cinquième année. ACT 2025 - Cours 11

Exemple 3: (suite) Ce montant accumulé est 1000(1. 04)(1. 045)2(1. 05)2 + 1000(1. 045)(1. 05) + 1000(1. 045) c’est-à-dire 5750. 44$. ACT 2025 - Cours 11

Considérons la deuxième situation, celle d’une annuité pour laquelle le taux d’intérêt ik est applicable au ke paiement et est le même pour ce paiement pour chaque période. L’annuité consiste en des paiements de 1$ à la fin de chaque période. ACT 2025 - Cours 11

Dans cette situation, la valeur actuelle de l’annuité sera Par analogie, nous noterons ceci par ACT 2025 - Cours 11

La valeur accumulée immédiatement après le dernier paiement sera Par analogie, nous noterons ceci par ACT 2025 - Cours 11

Exemple 4: Supposons que le premier paiement est rémunéré au taux de 6% par année, le second au taux de 5%, la troisième au taux de 5. 5% et le quatrième au taux de 6% et que tous les montants sont de R dollars. Que doit être R si nous voulons accumuler 20000$? ACT 2025 - Cours 11

Exemple 4: (suite) Nous avons l’équation de valeur à t = 4 ans Nous obtenons ainsi que R = 4599. 27$ ACT 2025 - Cours 11

Nous allons maintenant considérer des annuités pour lesquelles périodes de paiement et de capitalisation de l’intérêt sont différentes, soit la période de paiement est plus courte que celle de capitalisation de l’intérêt, soit la période de paiement est plus longue que celle de capitalisation de l’intérêt. ACT 2025 - Cours 11

Hypothèse: Si la période de paiement est plus courte que celle de capitalisation de l’intérêt, nous allons supposer qu’il y a un nombre entier de périodes de paiement dans une période de capitalisation de l’intérêt. ACT 2025 - Cours 11

Hypothèse: Si la période de paiement est plus longue que celle de capitalisation de l’intérêt, nous allons supposer qu’il y a un nombre entier de périodes de capitalisation de l’intérêt dans une période de paiement. ACT 2025 - Cours 11

Dans une telle situation, nous allons développer deux approches. Dans la première, il suffira de convertir le taux d’intérêt à un taux équivalent. Dans la seconde, nous développerons une approche théorique ACT 2025 - Cours 11

Première approche : Il suffit de convertir le taux d’intérêt de façon à obtenir le taux d’intérêt équivalent et pour lequel la période de capitalisation est la même que la période de paiement. Nous allons illustrer ceci dans des exemples. ACT 2025 - Cours 11

Exemple 5: Nous voulons accumuler 50 000$ en faisant 84 versements mensuels au montant de R dollars pendant 7 ans dans un fonds de placement. Le taux d’intérêt du fonds de placement est le taux nominal d’intérêt i(2) = 6% par année capitalisé semestriellement. Déterminons R. ACT 2025 - Cours 11

Exemple 5: (suite) Si i(2) = 6% alors le taux effectif d’intérêt équivalent est 6. 09% par année. De ceci nous obtenons que le taux nominal i(12) = 5. 926346437% par année capitalisé mensuellement est équivalent à i(2) = 6%. Conséquemment le taux d’intérêt par mois équivalent au taux i(2) = 6% est ACT 2025 - Cours 11

Exemple 5: (suite) Nous sommes maintenant dans la même situation que celle du chapitre 3. Conséquemment il nous faut donc déterminer R tel que Nous obtenons ainsi que R = 481. 73$ ACT 2025 - Cours 11