Hadrons and Nuclei Single Hadrons Lattice Summer School







































- Slides: 78

Hadrons and Nuclei : Single Hadrons Lattice Summer School Martin Savage Summer 2007 University of Washington

Mass Spectrum of Mesons | - M esons S= C = B = T = 0, qq ¼§ m ¼§ = 139: 57 Me. V ¼ 0 m ¼ 0 = 134: 96 Me. V ´ 0 m ´ = 548: 6 Me. V ´ 00 m ´ 0 = 957: 6 Me. V ½ 0; § m ½ = 770 Me. V ! 0 m ! = 783 Me. V ¿ = 2: 6 £ 10¡ ¿ = 0: 83 £ 10¡ 1 ¿¡ ¿¡ 1 s J ¼ = 0¡ 16 s J ¼ = 0¡ = 0: 9 ke. V J ¼ = 0¡ 1 ¿¡ 8 = 0: 3 Me. V J ¼ = 0¡ = 154 Me. V J ¼ = 1¡ = 9: 9 Me. V J ¼ = 1¡ Á0 m Á = 1020 Me. V A 1 m A 1 = 1275 Me. V ¿¡ 1 » 300 Me. V J ¼ = 1+ m J =à = 3: 1 Ge. V ¿¡ 1 = 88 ke. V J ¼ = 1¡ J=à ¨ m ¨ = 9: 5 Ge. V ¿¡ ¿¡ 1 1 = 4: 2 Me. V J ¼ = 1¡ = 52 ke. V J ¼ = 1¡

Mass Spectrum of Light Baryons | - B ar yons S = C = B = T = 0, qqq p m p = 938: 28 Me. V n m n = 939: 57 Me. V ¢ m ¢ » 1230 Me. V ¿> 1033 yr s J¼ = 1+ 2 ¿ = 898 § 16 s J ¼ = ¿¡ 1 » 120 Me. V J ¼ = 3+ 2 | - B ar yons S = 1 C = B = T = 0, sqq ¤ m ¤ = 1115: 6 Me. V ¿ = 2: 6 £ 10¡ §§ m § § = 1197: 3 Me. V § 0 m § 0 = 1192 Me. V 10 s ¿ = 1: 5 £ 10¡ ¿ = 6 £ 10¡ 20 s = J¼ 10 s 1+ 2 J¼ = 1+ 2

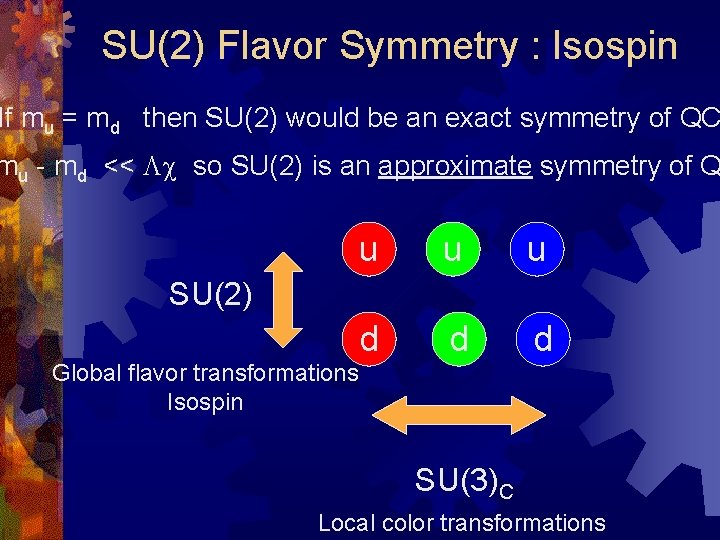
SU(2) Flavor Symmetry : Isospin If mu = md then SU(2) would be an exact symmetry of QC mu - md << Lc so SU(2) is an approximate symmetry of Q u u u d d d SU(2) Global flavor transformations Isospin SU(3)C Local color transformations

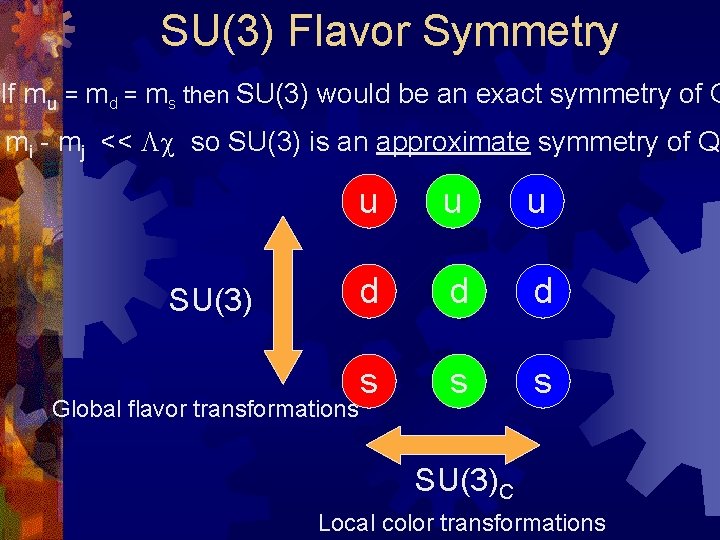
SU(3) Flavor Symmetry If mu = md = ms then SU(3) would be an exact symmetry of Q mi - mj << Lc so SU(3) is an approximate symmetry of Q SU(3) Global flavor transformations u u u d d d s s s SU(3)C Local color transformations

Mesons : SU(2) qa = M ab () u d µ Vq Vector symmetry : L = R = V = qb° 5 qa ¡ M M = q 1 2 ±ab qc ° 5 qc VMV p ¶ ¼ 0 = 2 ¼+ p = ¼¡ ¡ ¼ 0 = 2 p 1 ¼a ¿a 2

Mesons : SU(3) qa = M ab () u d s q = qb° 5 qa ¡ M 1 3 Vq ±ab qc ° 5 qc VMV p p 1 + + 0 ¼ = 2+ ´= 6 K p¼ p ¼¡ ¡ ¼ 0 = 2 + ´ = 6 K 0 A M = @ 0 K¡ K ¡ 2=6´ 0 ( Lectures by Claude Bernard )

Meson Correlation Functions and Interpolating Fields Z ^ y)i h. O(x; e. g. ¼+ » ^ y) ei Dq Dq DA ¹ O(x; ¡ ¢y hd(x)° 5 u(x) d(y)° 5 u(y) i = = R d 4 z L ( q; q; A ¹ ) h. Tr [ D (x ! y) ° 5 U(y ! x) ° 5 ]i £ ¤ y h. Tr D (x ! y) U (x ! y) i d-quark propagator u-quark propagato Z d 3 xhd(x)° 5 u(x) ¡ ¢y d(y)° 5 u(y) i ! e¡ m ¼ t E Z¼ + : : 2 m ¼

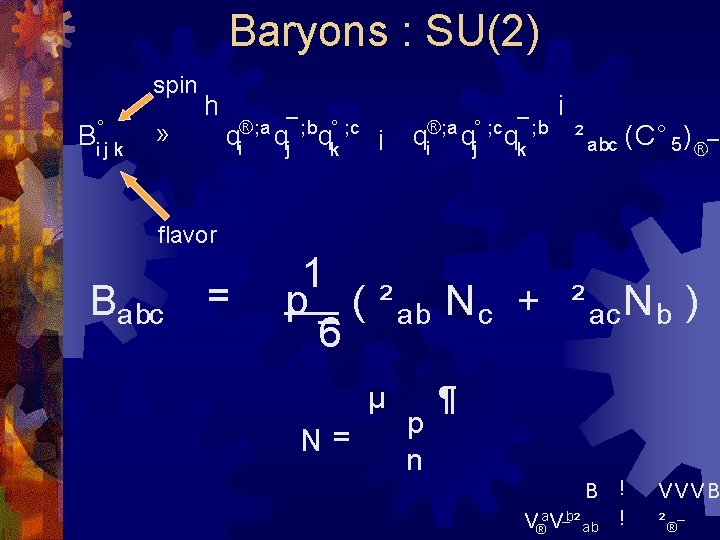
Baryons : SU(2) spin Bi°j k » h qi®; a qj¯ ; bqk° ; c ¡ qi®; a qj° ; c qk¯ ; b i ² abc (C° 5 ) ®¯ flavor Babc = 1 p ( ² ab N c + ² ac N b ) 6 µ N= p n ¶ B V®a V¯b² ab ! ! VVVB ² ®¯

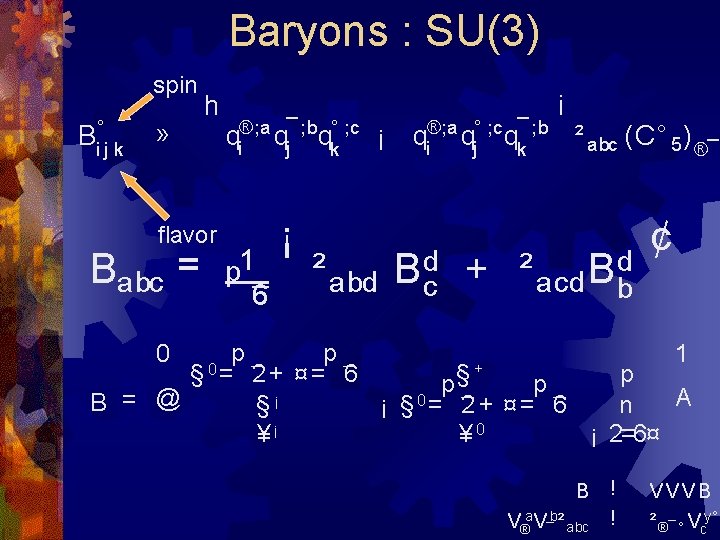
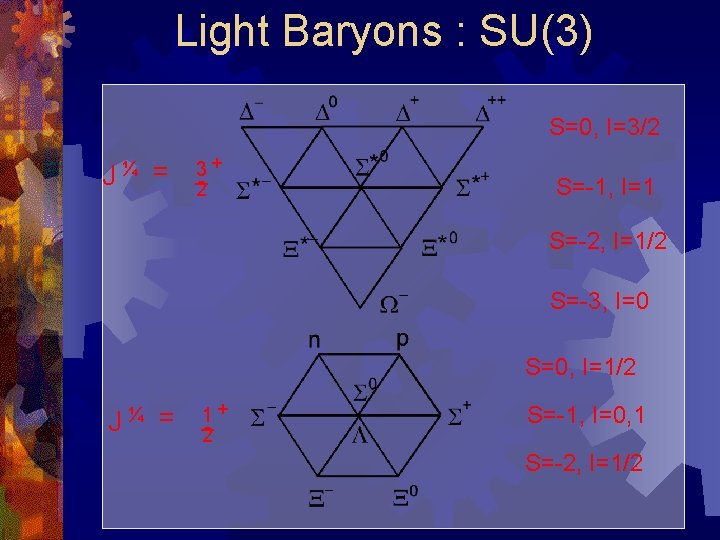
Baryons : SU(3) spin Bi°j k » h flavor Babc = 0 B = @ qi®; a qj¯ ; bqk° ; c ¡ p 1 6 p § 0= ¡ qi®; a qj° ; c qk¯ ; b i ² abc (C° 5 ) ®¯ ² abd B dc + ² acd B db ¢ p 1 + 2+ ¤= 6 p p§ p A §¡ ¡ § 0= 2 + ¤ = 6 n ¥¡ ¥ 0 ¡ 2=6¤ B V®a V¯b² abc ! ! VVVB ² ®¯ ° Vcy°

Light Baryons : SU(3) S=0, I=3/2 J¼ = 3+ 2 S=-1, I=1 S=-2, I=1/2 S=-3, I=0 S=0, I=1/2 J¼ = 1+ 2 S=-1, I=0, 1 S=-2, I=1/2

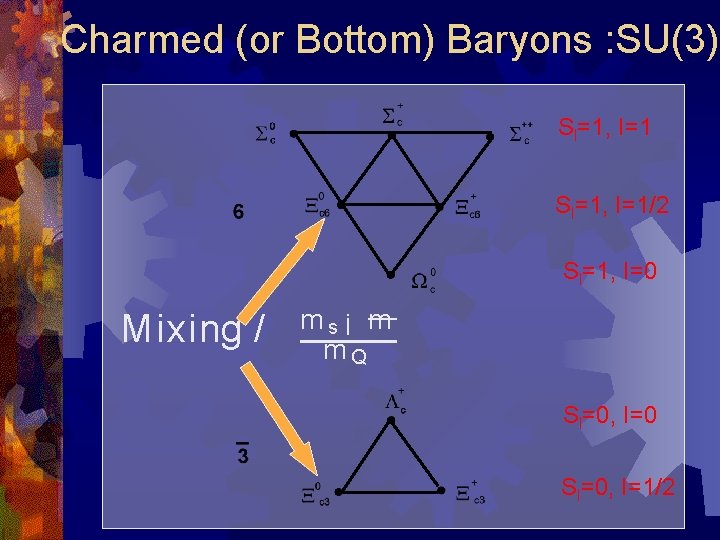
Charmed (or Bottom) Baryons : SU(3) Sl=1, I=1/2 Sl=1, I=0 Mixing / ms¡ m m. Q Sl=0, I=0 Sl=0, I=1/2

Light Quark Masses and Spurions ¹ = q i°¹ @q ¡ L SU(3) invariant 0 0 mu mq = @ 0 md 0 0 BUT : let m q ! qm q q breaks SU(3) 1 0 0 A ms V m q V y and t hen bot h t erms are SU(3) invariant T hen we can simply use t he W igner-Eckhart T heorem t o const ruct invariant mat rix element s.

p, K, h Masses : Gell-Mann—Okubo Mass Relation L = = ® T r [ M M mq ] + ¯ T r [ M M ] Tr [ mq ] + : : ¡ m 2¼ ¼+ ¼¡ + : : Construct all possible group invariants that can contribute More insert ions of M and m q m 2¼ = 2® m + 2¯(2 m + m s ) m 2 K = ® (m + m s ) + 2¯(2 m + ms ) m 2´ = 2® 3 2 4 m K (m + 2 m s ) + 2¯(2 m + m s ) ¡ 2 m¼ = 3 m 2´

p, n, L, S, X Masses : Gell-Mann—Okubo Mass Relation L = MN £ ¤ ¡ M 0 Tr B B ¡ ® T r B m q B £ ¤ ¡ ¯ T r B B mq ¡ ° T r B B T r [ m q ] + : : = M 0 + (2 m + m s )° + m® + m s ¯ 2 M N + 2 M ¥ = M § + 3 M ¤

Quark Masses from Lattice ( Claudes lectures ) m u =m d M s =m = = 0: 43 § 0: 01 § 0: 08 27: 4 § 0: 1 § 0: 4 § 0: 0 § 0: 1 MILC collaborat ion , ¹ = 2 Ge. V

Homework 1 : ® Check the validity of GMO mass relation amongst the pseudo-Goldstone bosons using Particle Data group compliations. ® What is the violation as a percent of the pion mass? the masses of the S, L , X at oneinsertion of the light quark mass matrix ® Derive

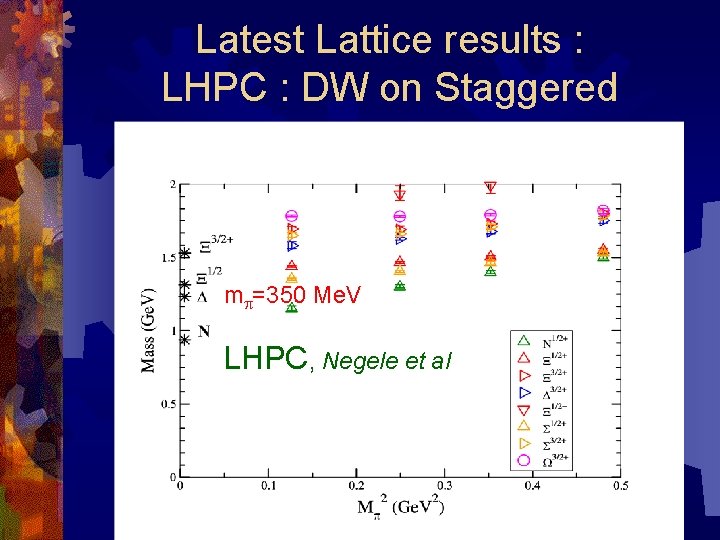
Latest Lattice results : LHPC : DW on Staggered mp=350 Me. V LHPC, Negele et al

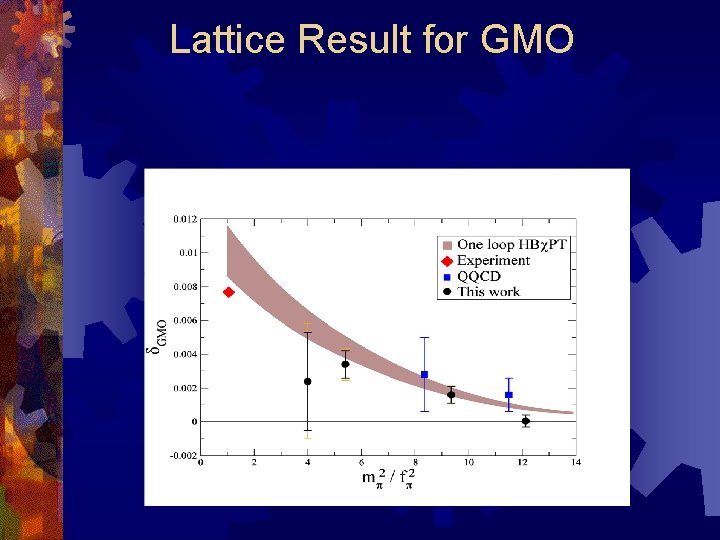
Lattice Result for GMO

Electromagnetism ¹ j em = = 0 Q = 2 ¹ u° u ¡ 3 q Q °¹ q 2 3 + @ 0 0 1 ¹ d° d ¡ 3 1 0 ¡ 1 3 0 Singlet plus Triplet of SU(2) Q = spurion field 1 ¹ s° s 3 0 0 A ¡ 1 3 Octet of SU(3) Q ! V QV y

Magnetic Moments in SU(3): Coleman-Glashow Relations L = £ ¹ F Tr B ¾¹ º F¹ º ¤ £ [Q; B ] + ¹ D Tr B ¾¹ º F¹ º ¤ f Q; B g Limit of exact SU(3) symmetry…. mu=md=ms ¹N = ¹F + 1 3 ¹D ¹ p ; ¹ n ; ¹ ¤ ; ¹ § + ; ¹ § ¡ ; ¹ ¥ 0 ; ¹ ¥¡ ; ¹ § ¤

Magnetic Moments : Coleman-Glashow Relations L ¹ §+ = ¹ p 2¹ ¤ = ¹ n ¹ ¥ 0 = ¹ n ¹ §¡ + ¹ n = ¡ ¹ p ¹ ¥¡ = ¹ §¡ p 2¹ ¤ § 0 = 3¹ n : : : = e ¹ i B ¾¹ º F ¹ º B 4 M N 2: 42 § 0: 05 NM = 2: 7928 NM ¡ 1: 226 § 0: 008 NM = ¡ 1: 9130 NM ¡ 1: 25 § 0: 01 NM = ¡ 1: 9130 NM ¡ 3: 07 § 0: 03 NM = ¡ 2: 7928 NM ¡ 0: 6507 § 0: 0025 NM = ¡ 1: 16 § 0: 03 NM 3: 22 § 0: 16 NM = 3: 31 NM Works as well as can be expected for SU(3) symmetry

Homework 2 : ® Explore the validity of the Coleman-Glashow relations between the magnetic moments of the baryon octet. ® Find analogous relations between the baryon decuplet, and find relations between the EM transition rates between the decuplet and octet assuming M 1 transition.

Matrix Elements in Nucleon (1) · = hpjq. Q° ¹ qjpi Up F 1( p) ° ¹ + F 2( p) i ¾¹ º qº + F 3( p) q¹ 2 M N Fi( p) @¹ j ¹ ( p) F 1 (0) ( p) F 2 (0) CONSTRAINTS ( p) 2 F 3 (q ) = 0 ! = +1 = · p = ( 2: 79 ¡ ´ GE = F 1 ¡ F 2 Up Fi( p) (q 2 ) = 0 1 ) NM Similarly for the neutron j. Q 2 j 4 M N 2 ¸ GM = F 1 + F 2

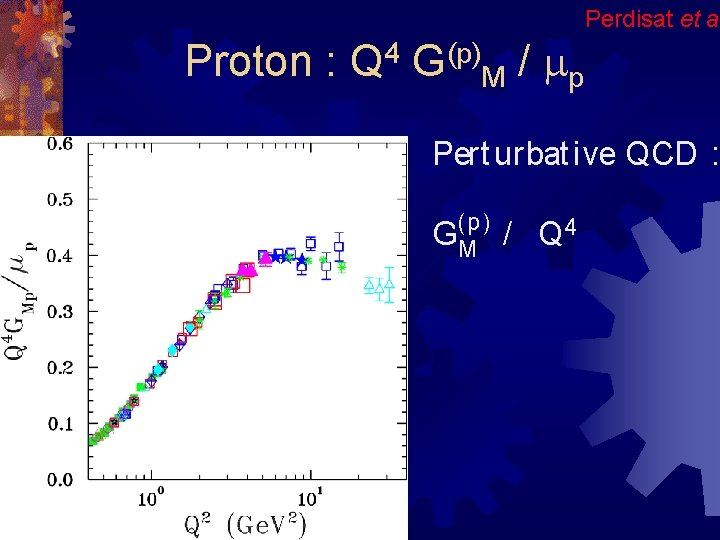
Perdisat et al Proton : 4 Q (p) G M / mp Pert urbat ive QCD : ( p) GM / Q 4

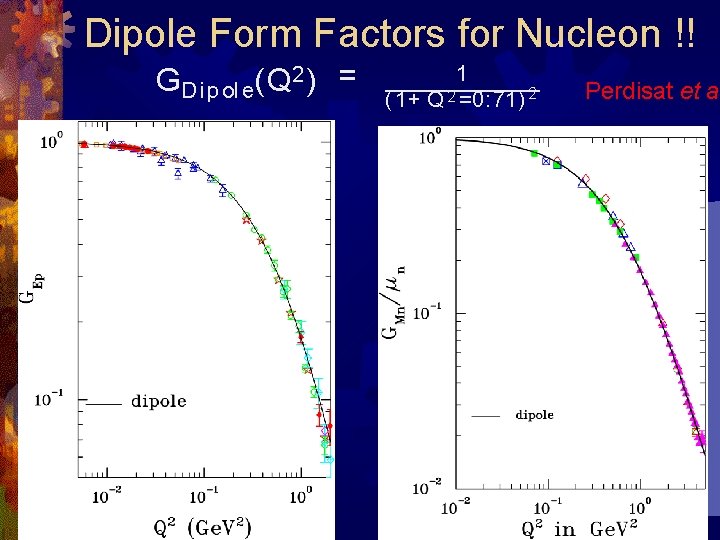
Dipole Form Factors for Nucleon !! GD i p ol e(Q 2 ) = 1 ( 1+ Q 2 =0: 71) 2 Perdisat et al

Recent Comprehensive Lattice Study : S. Boinepalli et al. , hep-lat/0604022 ® Clover on Quenched ® Not QCD (unfortunately), likely close to nature from all previous experiences. ® Clover gives O(a 2) errors in the quarks ® Good step toward fully-dynamical ® Disconnected diagrams evaluated phenomenologically…. . computationally expensive

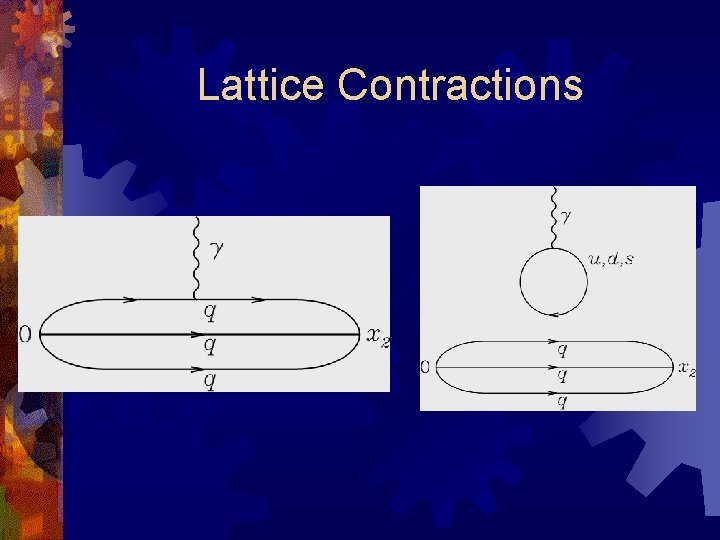
Lattice Contractions

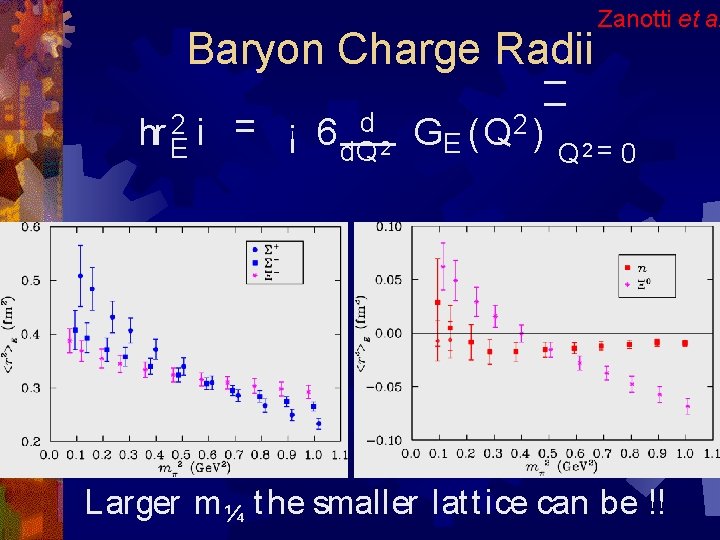
Baryon Charge Radii hr E 2 i = ¡ 6 d. Qd 2 Zanotti et al ¯ GE (Q 2 ) ¯ Q 2 = 0 Larger m ¼ t he smaller lat t ice can be !!

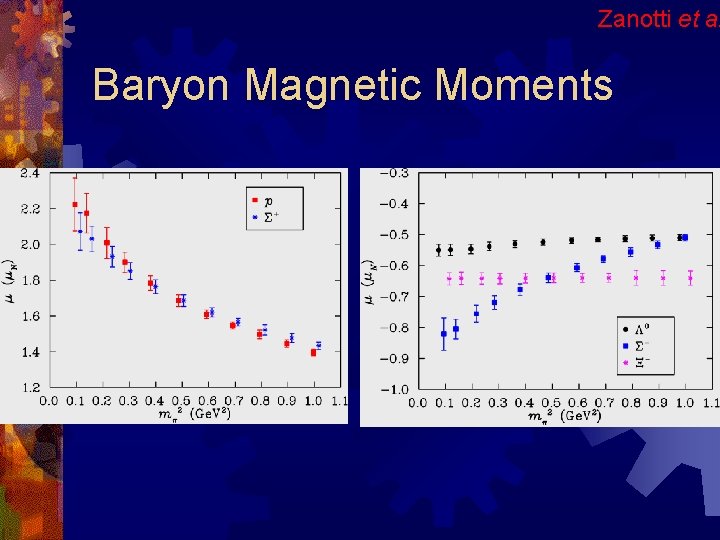
Zanotti et al Baryon Magnetic Moments

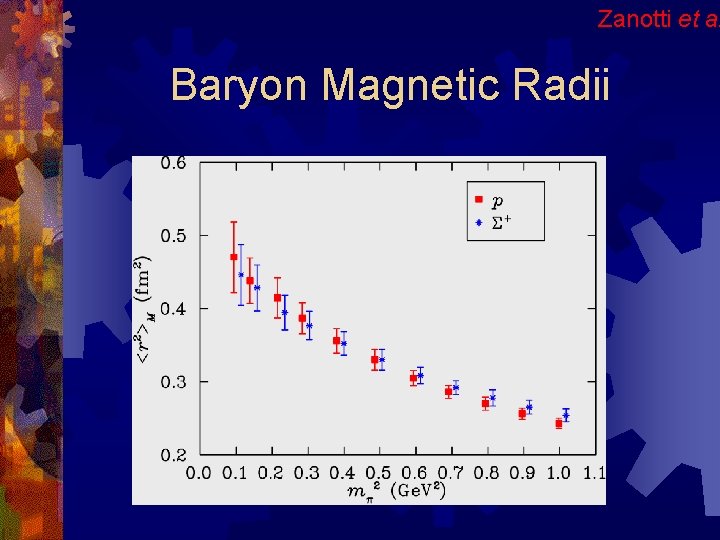
Zanotti et al Baryon Magnetic Radii

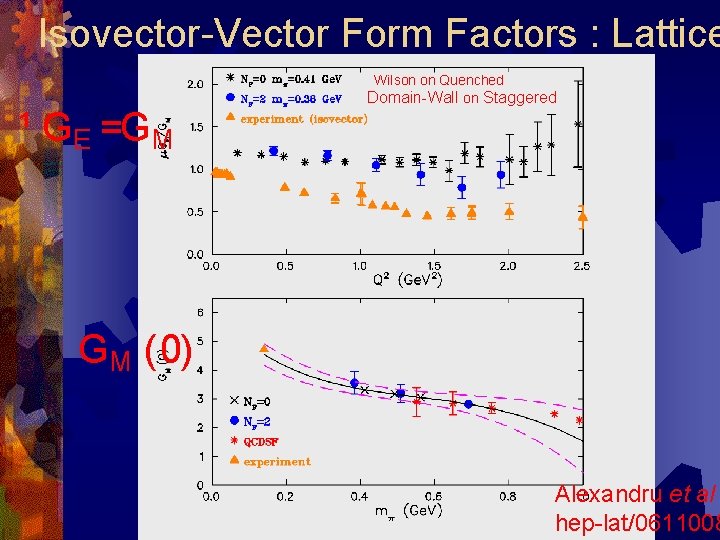
Isovector-Vector Form Factors : Lattice ¹ GE =GM Wilson on Quenched Domain-Wall on Staggered GM (0) Alexandru et al hep-lat/0611008

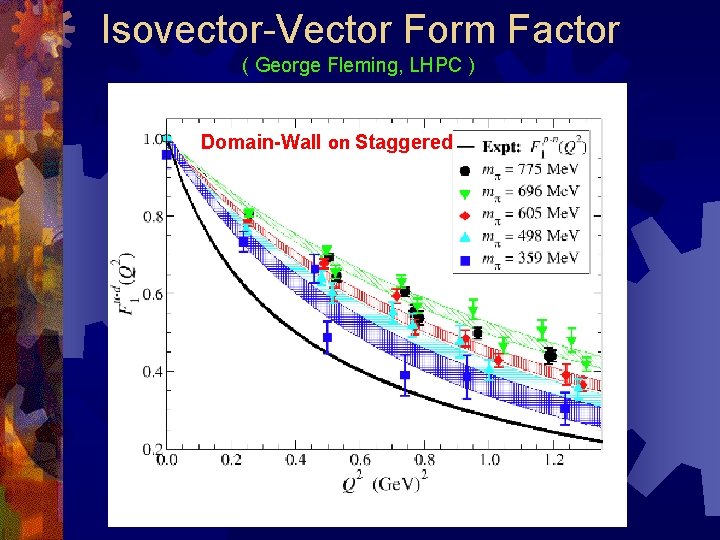
Isovector-Vector Form Factor ( George Fleming, LHPC ) Domain-Wall on Staggered

Just how Strange is the Proton ?

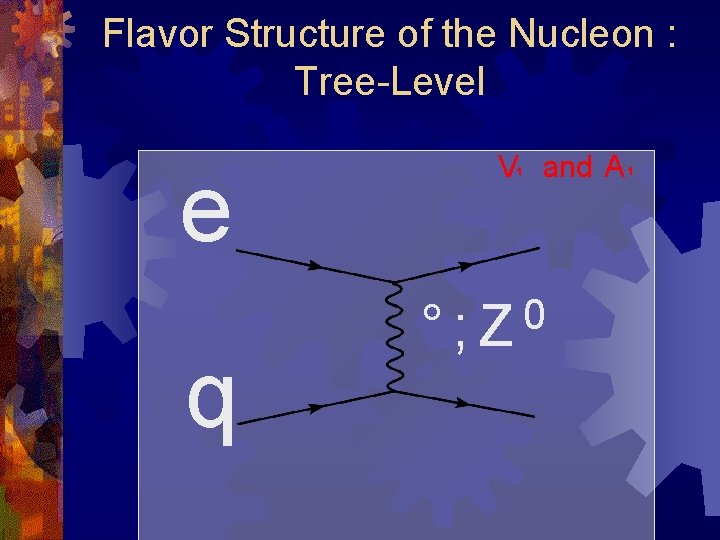
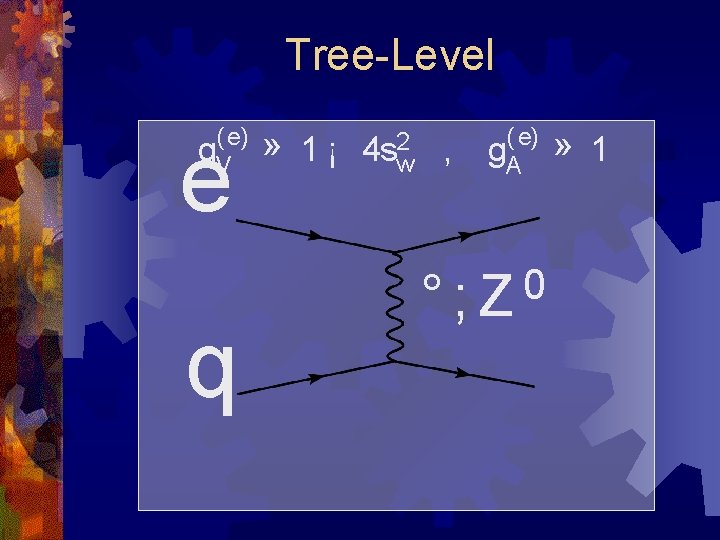
Flavor Structure of the Nucleon : Tree-Level e q V¹ and A ¹ 0 °; Z

Relevant parts of the Standard Model D ¹ = @¹ + i g 2 W¹a T a + i g 1 12 Y B ¹ ¡ ¢ 2 Z D ¹ = @¹ + i e. QA ¹ + i s ec T 3 ¡ Qsw ¹ w t an µw B¹ = p 1 g 12 + g 22 W¹ 3 = p YÁ = + 1 1 g 12 + g 22 = w g 1 g 2 (g 1 Z ¹ + g 2 A ¹ ) (g 1 A ¹ ¡ g 2 Z ¹ ) µ hÁi = 0 p v= 2 ¶

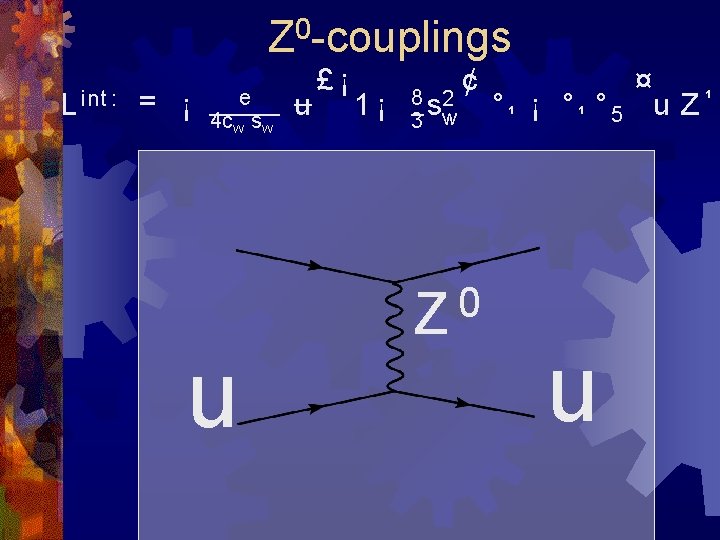
0 Z -couplings L int : = ¡ e 4 cw sw u u £¡ 1¡ 8 s 2 3 w ¢ 0 Z ¤ °¹ ¡ °¹ ° 5 u Z¹ u

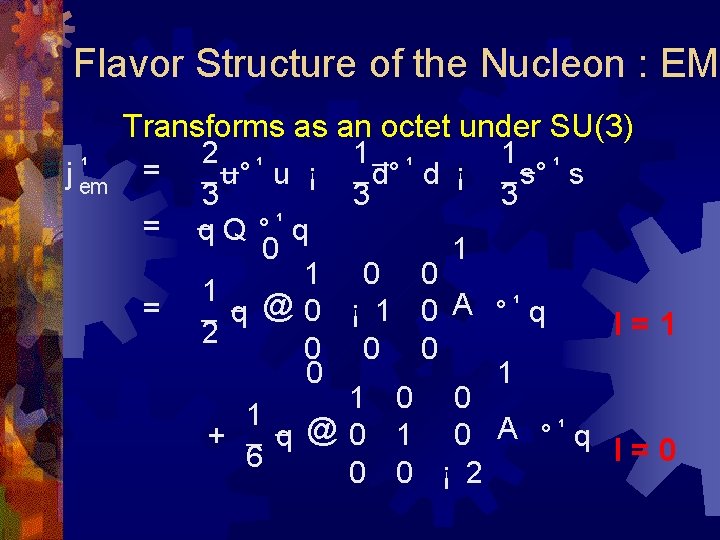
Flavor Structure of the Nucleon : EM ¹ j em Transforms as an octet under SU(3) 2 ¹ 1 ¹ = d° d ¡ u° u ¡ s° s 3 3 3 = q Q °¹ q 0 1 1 0 0 1 @ = 0 ¡ 1 0 A °¹ q q I=1 2 0 0 1 1 0 0 1 @ 0 1 0 A °¹ q I = 0 q + 6 0 0 ¡ 2

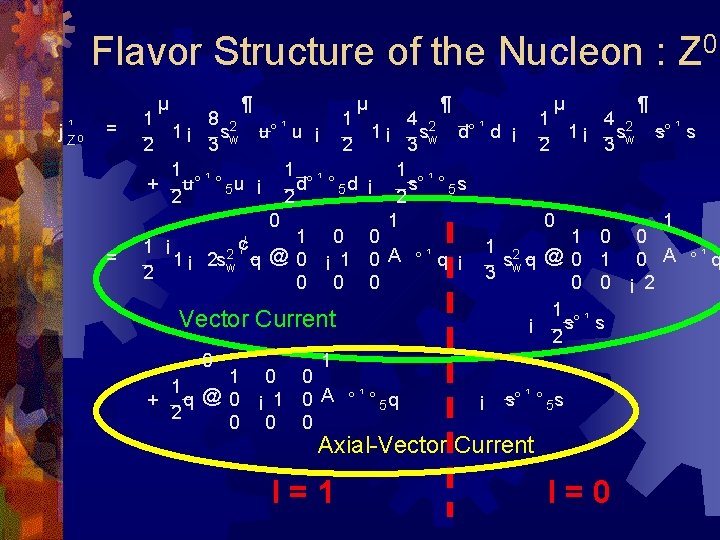
Flavor Structure of the Nucleon : Z 0 µ j Z¹ 0 = = ¶ µ 1 8 1 1 ¡ s 2 w u° ¹ u ¡ 2 3 2 1 1 ¹ d° ° 5 d + u° ¹ ° 5 u ¡ 2 2 0 1 0 ¢ 1 ¡ 2 q @ 0 ¡ 1 1 ¡ 2 sw 2 0 0 1¡ ¡ µ d° ¹ d ¡ 1 ¹ s° ° 5 s 2 1 0 0 A °¹ q ¡ 0 Vector Current 0 4 2 s 3 w ¶ 1 4 1 ¡ s 2 w 2 3 0 1 1 2 @ 0 s q 3 w 0 1 ¹ s° ¡ 2 ¡ 0 0 1 0 A °¹ q 0 ¡ 2 s s° ¹ ° 5 s Axial-Vector Current I=1 s° ¹ s 1 1 1 0 0 1 @ 0 ¡ 1 0 A ° ¹ ° 5 q + q 2 0 0 0 ¶ I=0

Matrix Elements in Nucleon (2) 0 1 1 0 0 hpjq @ 0 ¡ 1 0 A ° ¹ qjpi 0 0 0 = Up · ³ ´ F 1(p) ¡ F 1(n ) ° ¹ + ³ F 2(p) ¡ F 2(n ) ´ q i ¾¹ º º 2 M N ¸ Up Isovector 0 1 1 0 0 hpjq @ 0 1 0 A ° ¹ qjpi 0 0 ¡ 2 = · ³ 3 Up F 1( p) + F 1( n ) ° ¹ + · hpjs° ¹ sjpi = Up ´ F 1( s) (q 2 )° ¹ ³ F 2( p) + F 2( n ) ´ q i ¾¹ º º 2 M N ¸ Up Isoscalar ¸ qº ( s) 2 ¹ º + F 2 (q )i ¾ Up 2 M N strange CONSTRAINTS F 1( s) (0) = 0

Tree-Level ( e) g. V e q 2 , » 1 ¡ 4 sw ( e) g. A 0 °; Z » 1

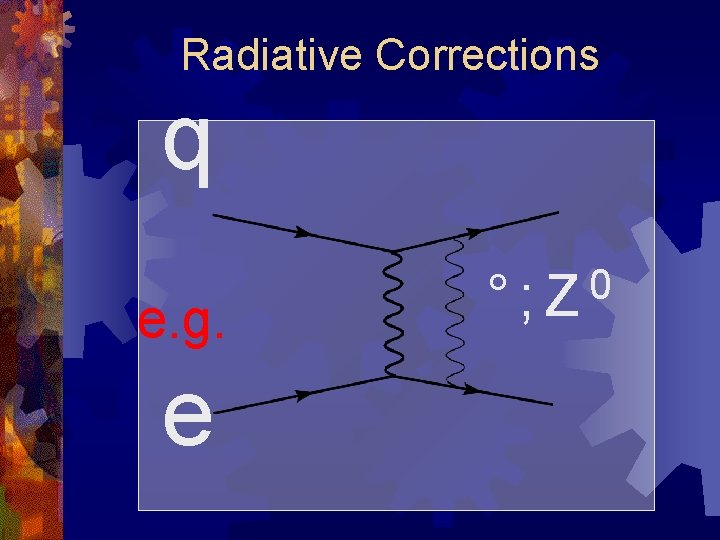
Radiative Corrections q e. g. e 0 °; Z

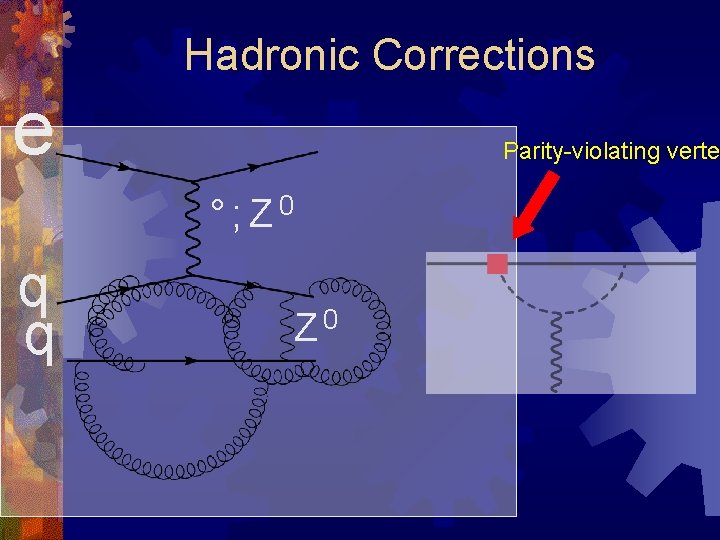
Hadronic Corrections e Parity-violating verte °; Z 0 q q Z 0

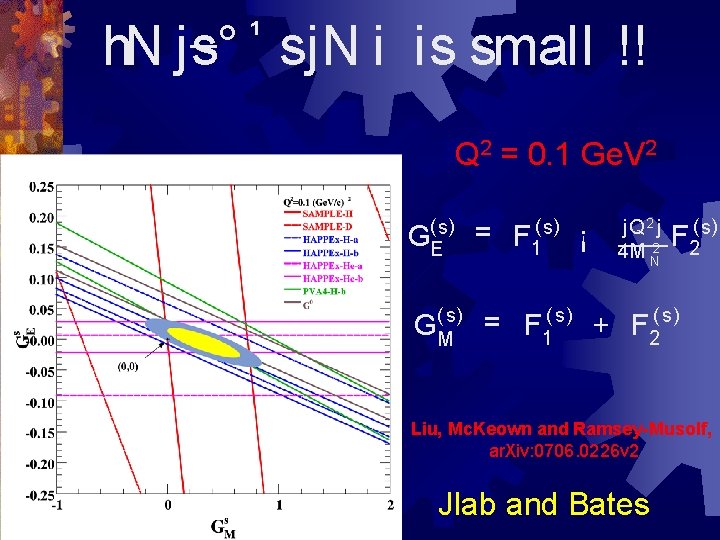
¹ h. N js° sj. N i is small !! Q 2 = 0. 1 Ge. V 2 GE(s) = F 1(s) ¡ j. Q 2 j 4 M N 2 F 2(s) G(Ms) = F 1( s) + F 2( s) Liu, Mc. Keown and Ramsey-Musolf, ar. Xiv: 0706. 0226 v 2 Jlab and Bates

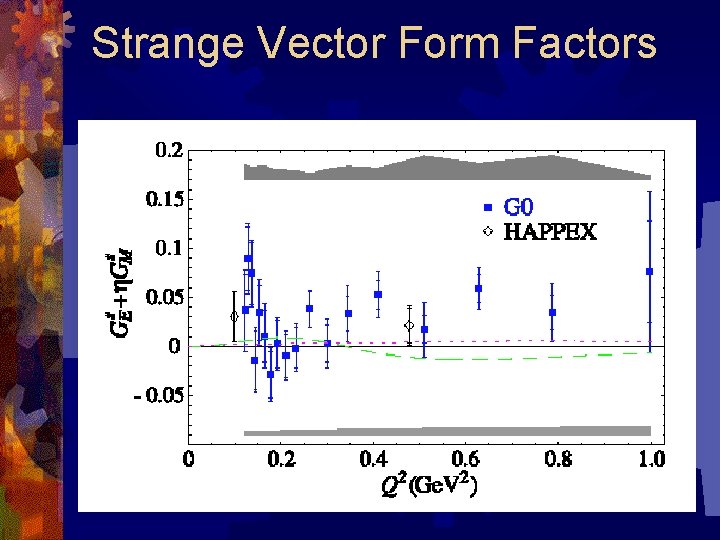
Strange Vector Form Factors

Axial-Current Matrix Elements in Nucleon (1) · hpju° ¹ ° 5 djni = Up g 1 (q 2 )° ¹ ° 5 q + g 2 (q 2 )i ¾¹ º ° 5 º + g 3 (q 2 )° 5 q¹ 2 M N CONSTRAINTS T and I g 1 (0) ! g 2 (q 2 ) = 0 = g. A ¯ ¡ decay ¸ Un

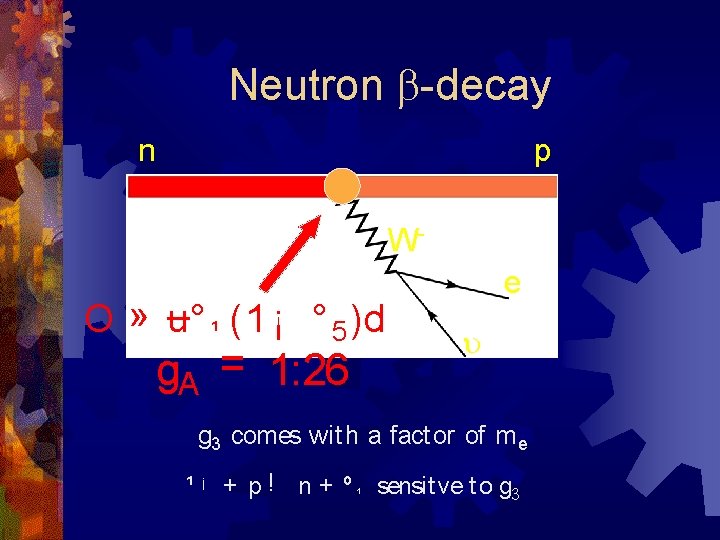
Neutron b-decay n p W- O » u° ¹ (1 ¡ ° 5 )d g. A = 1: 26 e u g 3 comes wit h a fact or of m e ¹ ¡ + p ! n + º ¹ sensit ve t o g 3

PCAC p Am a A ¹ (x) = q° ¹ ° 5 a T q(x) h 0 j. A ¹a (x)j¼b(q)i = ¡ i f ¼ q¹ e¡ h 0 j@¹ A ¹a (x)j¼b(q)i = ¡ f ¼ m 2¼ e¡ @¹ A ¹a (x) = ¡ f ¼ m 2¼ ¼a (x) i q: x ±ab T herefore @¹ A ¹ is a good int erpolat ing ¯eld for t he pion.

PCAC : Goldberger-Treiman (1) (1958) h. N j. A a¹ (x)j. N i = h. N j@¹ A a¹ (x)j. N i = U [ g 1 ° ¹ ° 5 + g 3 q¹ ° 5 ] T a U e¡ i q: x £ ¤ a ¹ 2 ¡ i U g 1 q ° ¹ ° 5 + g 3 q ° 5 T U e¡ i q: x In chiral limit, @¹ A a¹ = 0 hence 2 M N g 1 (q 2 ) + q 2 g 3 (q 2 ) = 0

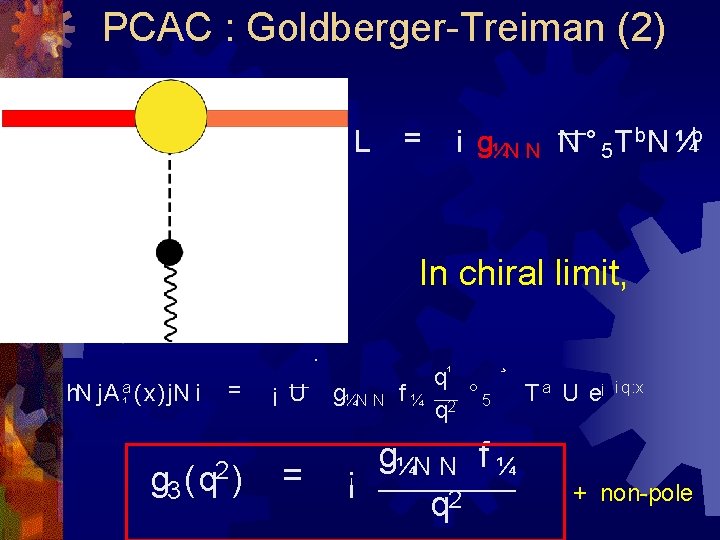
PCAC : Goldberger-Treiman (2) L = i g¼N N N ° 5 T b. N ¼b In chiral limit, · h. N j. A a¹ (x)j. N i g 3 = (q 2 ) ¡ U = g¼N N f ¼ q¹ q 2 ¸ ° 5 g¼N N f ¼ ¡ q 2 T a U e¡ i q: x + non-pole

PCAC : Goldberger-Treiman (3) In chiral limit, g¼N N f ¼ 2 g 3 (q ) = ¡ q 2 2 M N g 1 (q 2 ) + q 2 g 3 (q 2 ) = g 1 (q 2 ) = 0 g¼N N f ¼ 2 M N Away from the chiral limit, g 3 (q 2 ) = g¼N N f ¼ ¡ 2 q ¡ m 2¼ g 1 (q 2 ) = g¼N N f ¼ m 2¼ + O( 2 ) 2 M N ¤

PCAC : Goldberger-Treiman (4) At the physical point, g 3 (q 2 ) g 1 (q 2 ) = = g¼N N f ¼ ¡ 2 q ¡ m 2¼ g¼N N f ¼ + O( 2 ) 2 M N ¤ g. A g¼N N 2 M N g. A 1¡ f ¼g¼N N Sid Coon, Nucl-th/9906011 = = 1: 2654 § 0: 0042 13: 12 ; 13: 02 = 0: 023 ; 0: 015

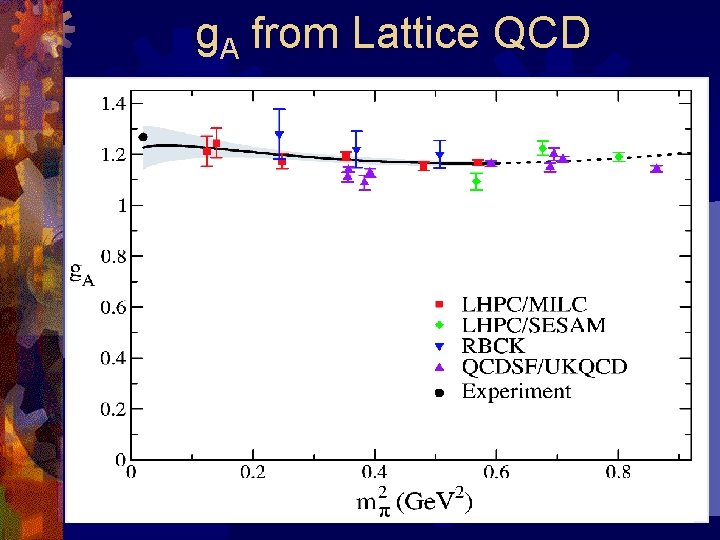
g. A from Lattice QCD

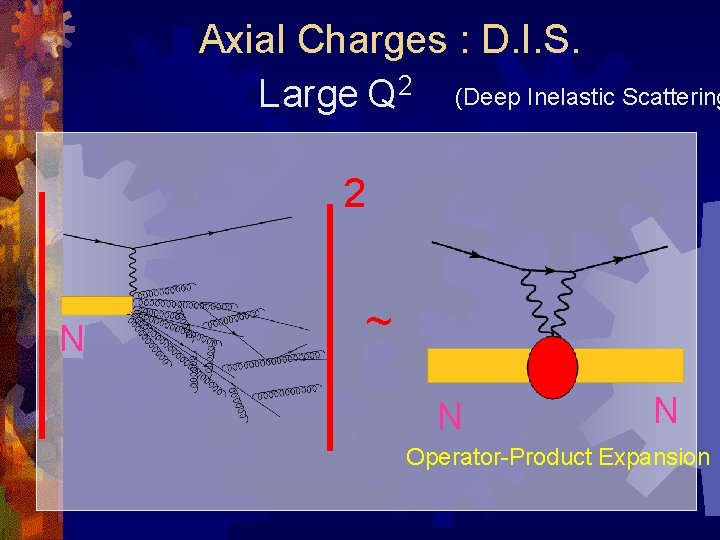
Axial Charges : D. I. S. Large Q 2 (Deep Inelastic Scattering 2 N ~ N N Operator-Product Expansion

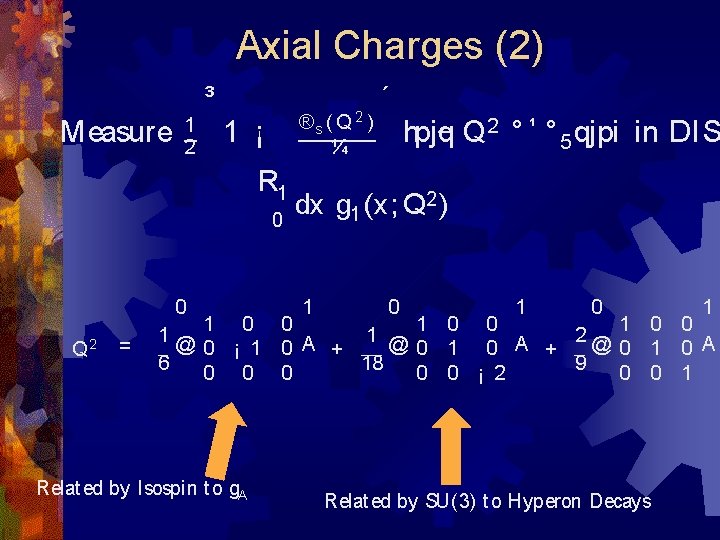
Axial Charges (2) Measure 1 2 ³ 2 ®s ( Q ) ¼ 1 ¡ R 1 0 0 Q 2 = ´ hpjq Q 2 ° ¹ ° 5 qjpi in DIS dx g 1 (x; Q 2 ) 1 0 1 1 0 0 1@ 1 2 @0 1 0 A + @0 1 0 A 0 ¡ 1 0 A + 6 18 9 0 0 0 ¡ 2 0 0 1 Relat ed by Isospin t o g. A Relat ed by SU(3) t o Hyperon Decays

Axial Charges (3) Including SU(3)-breaking ¡ 0: 35 < ¢ s < 0 ¡ 0: 1 < ¢ u + ¢ d + ¢ s < + 0: 3 2 ¢ q U p s¹ Up = hpjq° ¹ ° 5 qjpi

Nucleon s-Term (1) H^ (m q ) j. N (m q )i h. N (m q )j H^ (m q ) j. N (m q )i @ E (m q ) mq @mq L Q C D (m q ) = = Feynman-Hellman Thm E (m q )j. N (mq )i = E (m q ) = @ ^ H (m q ) j. N (m q )i h. N (m q )jm q @m q L Q C D (0) ¡ X m i qi qi i @ ^ mi H (m q ) @m i = H^ (m q ) = m i qi qi H^ (0) + X i @ ^ H (m q ) mi @m i

Nucleon s-Term (2) : SU(2) ¾N = X i @M N 2 = m¼ + : : mi 2 @m i @m ¼ = h. N (m q )j m u uu + m d dd j. N (m q )i = m h. N (m q )j uu + dd j. N (m q )i ¾N » 45 Me. V from scat t ering See later Not e t hat : h. N (m q )j. N (m q )i = 1 : convent ional t o use = 2 M N

Nucleon s-Term (3) : SU(3) ¾N = = h. N (m q )j m u uu + m d dd + m s ss j. N (m q )i 1 (2 m + m s ) h. N (m q )j uu + dd + ss j. N (m q )i 3 1 + (m ¡ m s ) h. N (m q )j uu + dd ¡ 2 ss j. N (m q )i 3 SU(3) Singlet SU(3) Octet

Nucleon s-Term (4) : strangeness m h. N (m q )juu + dd ¡ 2 ssj. N (m q )i » 35 § 5 Me. V · ¸ 2 m¼ 3 1 = (M ¥ ¡ M N ) ¡ (M § ¡ M ¤ ) 2 2 4 m. K ¡ m¼ 2 Using ¾N » 45 Me. V gives 2 h. N (m q )jssj. N (m q )i h. N (m q )juu + ddj. N (m q )i » 0: 2 ! 0: 4

Nucleon s-Term (5) h. N (m q )j m s ss j. N (m q )i » 130 Me. V h. N (m q )j H^ (0)j. N (m q )i » 764 Me. V Strange quarks (non-valence) play a nontrivial role on the structure of the Nucleon

s-Term from the Lattice Two methods used presently : 1. Compute MN and take numerical derivatives … poor precision…many configs (QCD) 2. Compute 3 -pt function

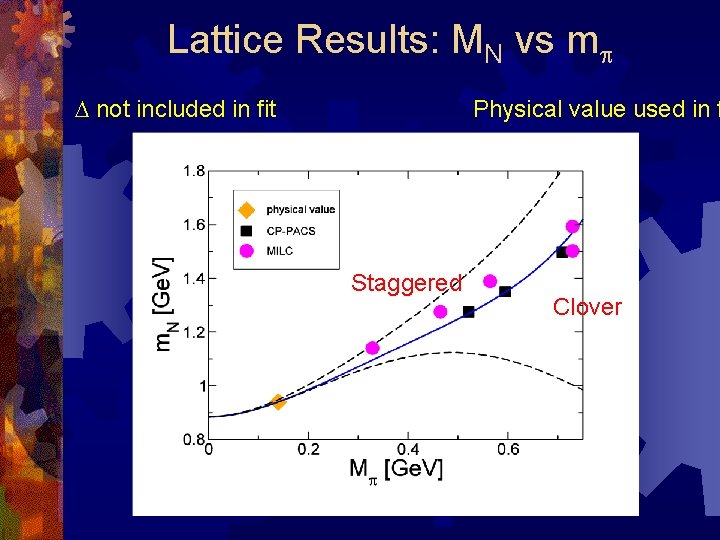
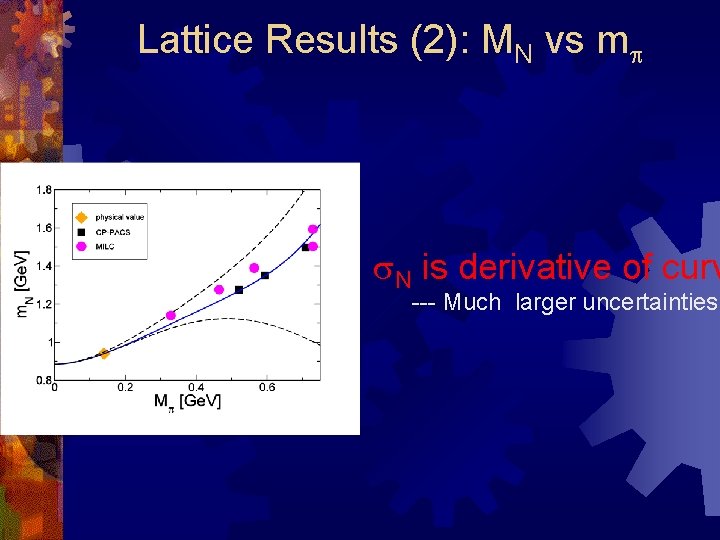
Lattice Results: MN vs mp D not included in fit Physical value used in f Staggered Clover

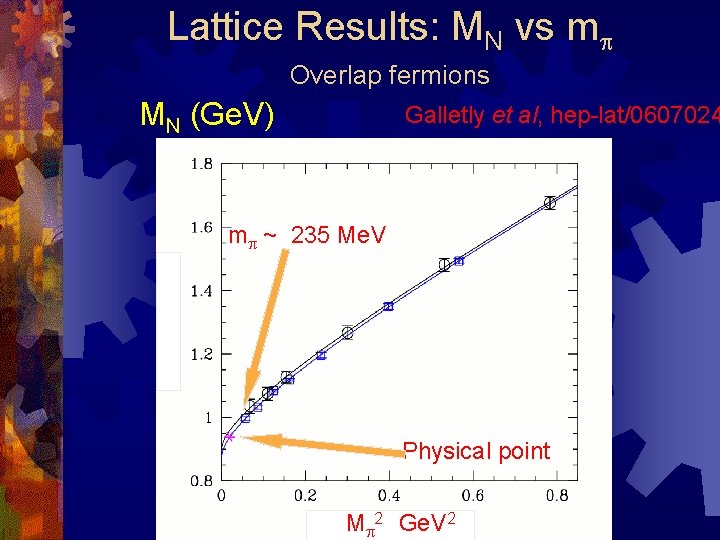
Lattice Results: MN vs mp Overlap fermions MN (Ge. V) Galletly et al, hep-lat/0607024 mp ~ 235 Me. V Physical point Mp 2 Ge. V 2

Lattice Results (2): MN vs mp s. N is derivative of curv --- Much larger uncertainties

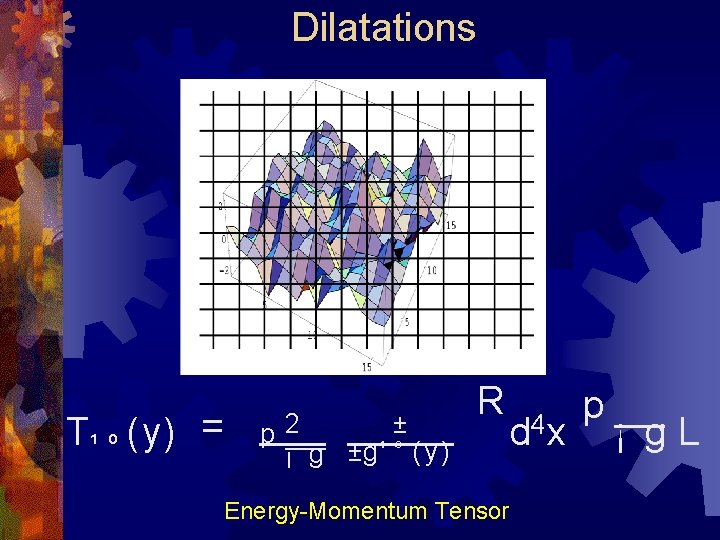
Dilatations T¹ º (y) = ± p 2 ¡ g ±g ¹ º ( y ) R Energy-Momentum Tensor d 4 x p ¡ g. L

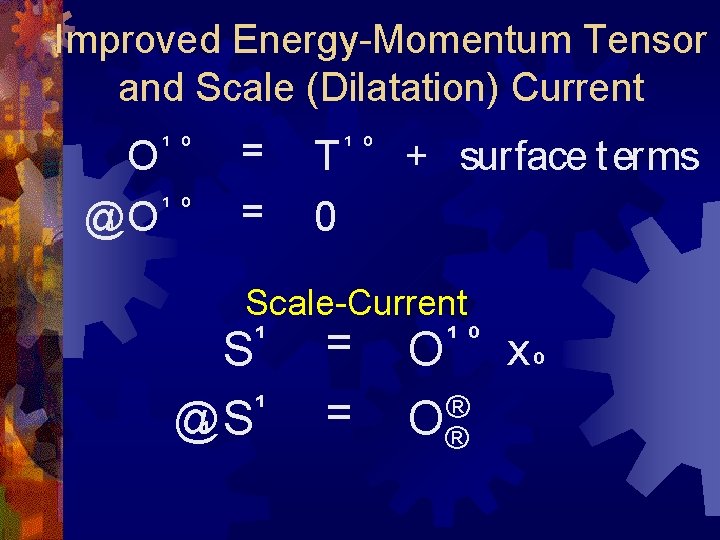
Improved Energy-Momentum Tensor and Scale (Dilatation) Current ¹ º O @¹ O ¹ º = = ¹ º T + surface t erms 0 Scale-Current ¹ S = ¹ º O ¹ @¹ S = ® O® xº

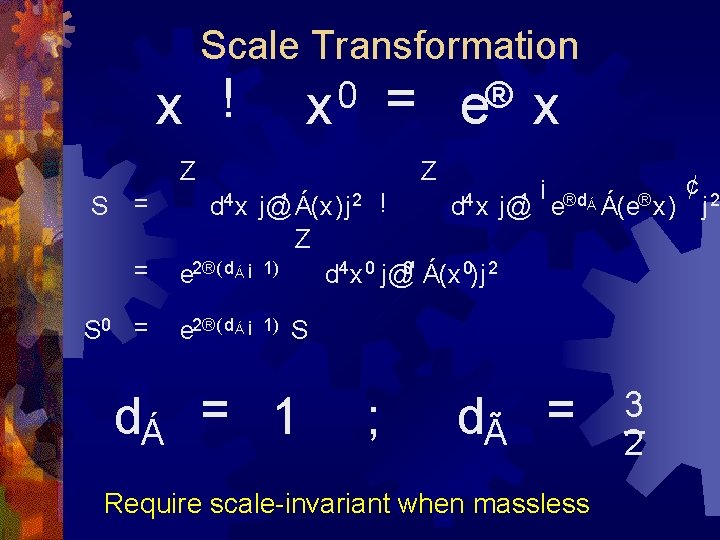
Scale Transformation x ! = e® x 0 x Z S = Z d 4 x j@¹ Á(x)j 2 ! d 4 x j@¹ ¡ e®dÁ Á(e® x) Z = e 2®( dÁ ¡ 1) S 0 = e 2®( dÁ ¡ 1) dÁ d 4 x 0 j@0¹ Á(x 0)j 2 S = 1 ; dà = Require scale-invariant when massless 3 2 ¢ j 2

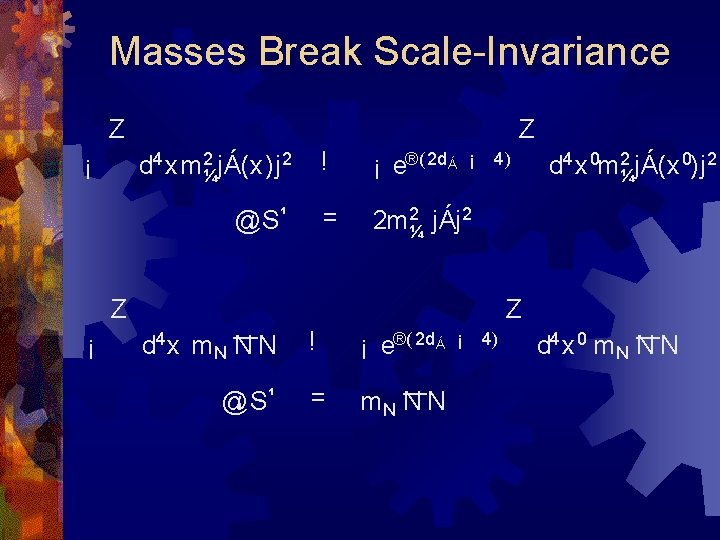
Masses Break Scale-Invariance Z Z d 4 xm 2¼jÁ(x)j 2 ¡ @¹ S¹ ! ¡ e®( 2 d Á = 2 m 2¼ jÁj 2 ¡ 4) Z ¡ d 4 x 0 m 2¼jÁ(x 0)j 2 Z d 4 x m N N N @¹ S¹ ! ¡ e®( 2 d Á = m. N N N ¡ 4) d 4 x 0 m N N N

Gauge Fields Renormalizat ion Scale ¹ relat ed t o coordinat es via ¹ » 1=x x ! 0 x g = g(Q 2 =¹ 2 ) ! g(¹ ) ! L = ±L ±® = = e® x g(e¡ 2® Q 2 =¹ 2 )) g(e® ¹ ) £ 2¤ 1 Tr G ¡ 4 g 2 QCD b-function £ 2¤ ¯ = @¹ S¹ Tr G 2 g 3

Nucleon Mass h. N j. O®® j. N i = M N £ 2¤ ¯ = h. N j Tr G j. N i + 3 2 g h. N j(1 ¡ ° u )m u uu + (1 ¡ ° d )m d dd + (1 ¡ ° s )m s ssj. N i Anomalous dimension = quantum corrections

Ademollo-Gatto Theorem (1964) ® Corrections to the matrix elements of a charge operator between states in the same irreducible representation first occur as the square of the symmetry breaking parameter ® True if matrix element is analytic function of breaking parameter ® ® NOT valid for vector current matrix elements in light hadrons due to IR behavior of QCD True for heavy quark symmetry. . Luke’s Theorem Vector Current Matrix elements between members of SU(3), SU(2) irreps are protected from symmetry breaking effects, since they are the charge operators

Ademollo-Gatto Theorem (1964) Z ^ ab Q Z = d 3 x qa (x)° 0 qb(x) = h h. K 0 j h ^us Q i ^us ; Q ^ su Q i ^ su j. K 0 i ; Q d 3 x qay ° 0 qb = ^uu ¡ Q ^ ss Q = ^uu ¡ Q ^ ss j. K 0 i h. K 0 j Q ³ P n ´ ^ u s jni hnj Q ^ su j. K 0 i ¡ h. K 0 j Q ^ su jni hnj Q ^ u s j. K 0 i = 0 ¡ (¡ 1) h. K 0 j Q ³ ´ ^ su j. K 0 i j 2 ¡ jhnj Q ^ u s j. K 0 i j 2 = 1 AND t ransit ions out side jhnj Q oct et are O(¸ ) =0 1¡ ¡ h¼ su 0 ^ j Q j. K i = O(¸ l = SU(3) breaking parameter 2)

Baryon Resonance Spectrum ® So far just discussed extracting the ground states from lattice calculations. ® What about excitations ® ® If stable, the correlation function has simple exponential form If unstable, volume dependence required… l (see later)

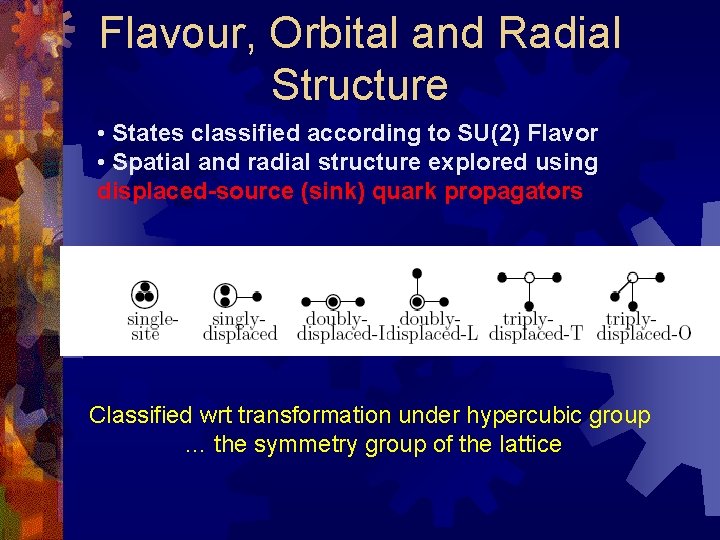
Flavour, Orbital and Radial Structure • States classified according to SU(2) Flavor • Spatial and radial structure explored using displaced-source (sink) quark propagators Classified wrt transformation under hypercubic group … the symmetry group of the lattice

Methodology: Luscher-Wolff Compute correlation matrix from the r sources and r sinks C®¯ (t; t 0 ) = h 0 j. O® (t) O¯ (t 0 )j 0 i The eigenvalues of A ¸i ! = p 1 C(t 0 ) are³ e¡ E i ( t ¡ t 0 ) C(t) p 1 C(t 0 ) 1 + e¡ ¢ E (t ¡ t 0 ) ´ min ( En – Ei) • Eigenvalues ! Energies = masses of stable particles, (or energy of scattering state for unstable particles) • Eigenvectors ! “wave functions”

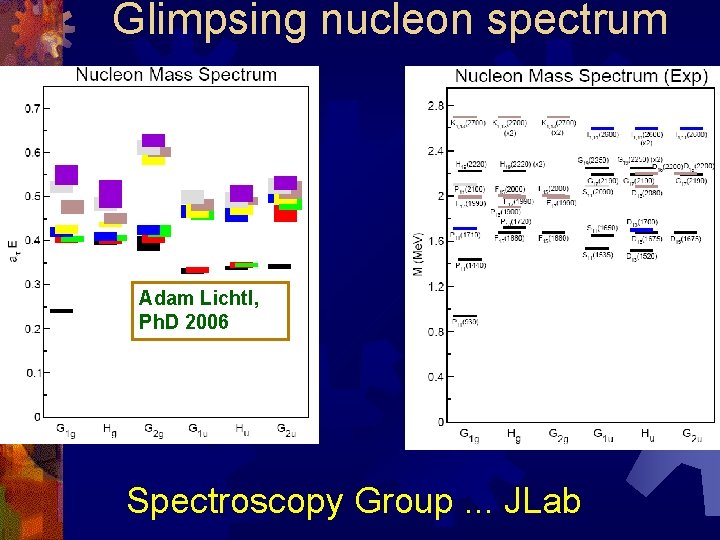
Glimpsing nucleon spectrum Adam Lichtl, Ph. D 2006 Spectroscopy Group. . . JLab

Summary ® Huge amount of phenomenology … traditionally the domain of nuclear physics (t > ~ 1970…QCD) ® ® Flavor structure Interactions Excitations Far fewer lattice calculations than for mesons ® ® Correlator falls much faster Signal degrades exponentially faster Requires significantly more effort … people-power and computers Relatively straighforward procedure to follow Go forth and compute the properties of the b blocks of nuclei from QCD !
 Hadrons
Hadrons Poset lattice
Poset lattice Summer school lodi unified
Summer school lodi unified Crescenta valley high school summer school
Crescenta valley high school summer school Assignment in spanish
Assignment in spanish Multiple instruction single data example
Multiple instruction single data example Dataxin
Dataxin Multi channel multi phase example
Multi channel multi phase example Harris peripheral model
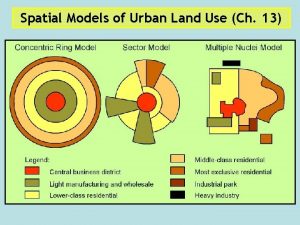
Harris peripheral model Homer hoyt sector model
Homer hoyt sector model Multiple nuclei model example
Multiple nuclei model example Who made the sector model
Who made the sector model Multiple nuclei model
Multiple nuclei model Harris and ullman multiple nuclei model
Harris and ullman multiple nuclei model Nmr active and inactive nuclei
Nmr active and inactive nuclei How unstable atoms gain stability
How unstable atoms gain stability Ivc summer classes for high school students
Ivc summer classes for high school students Ducksters
Ducksters Slam summer school
Slam summer school La sapienza summer school
La sapienza summer school Event management summer school
Event management summer school Upc summer school
Upc summer school Study abroad harvard summer
Study abroad harvard summer Td(0)
Td(0) Exotic beam summer school
Exotic beam summer school Purdue summer school
Purdue summer school Gene golub summer school
Gene golub summer school Dr kimberly higgins
Dr kimberly higgins Summer school 2013
Summer school 2013 Uct summer school
Uct summer school Cern summer school
Cern summer school кpi
кpi Snu summer school
Snu summer school Fluid intelligence examples
Fluid intelligence examples Wacqt summer school
Wacqt summer school Jtg summer school
Jtg summer school Summer school demokritos
Summer school demokritos Pkdkd
Pkdkd Invitation to summer school
Invitation to summer school Huntsville reading program
Huntsville reading program Carson graham summer school
Carson graham summer school Flames summer school
Flames summer school Sharcnet summer school
Sharcnet summer school Carpathian summer school of physics
Carpathian summer school of physics Santa fe institute summer school
Santa fe institute summer school Complex systems summer school
Complex systems summer school Belgrade summer school
Belgrade summer school Nice summer school
Nice summer school Neutron capture
Neutron capture Skku summer
Skku summer Asm201 course code
Asm201 course code Sutton trust summer school
Sutton trust summer school Slac summer school
Slac summer school Niagara catholic summer school
Niagara catholic summer school Rtu summer school
Rtu summer school Leysin summer school
Leysin summer school Imperial summer school engineering
Imperial summer school engineering Summer school cepal
Summer school cepal Alpbach summer school 2019
Alpbach summer school 2019 Cern summer school lectures
Cern summer school lectures Visegrad summer school
Visegrad summer school Fermilab summer school
Fermilab summer school Lattice vibrations and thermal properties of solids
Lattice vibrations and thermal properties of solids Prove that every chain is a distributive lattice
Prove that every chain is a distributive lattice Bragg's law in reciprocal lattice
Bragg's law in reciprocal lattice Coulomb's law and lattice energy
Coulomb's law and lattice energy Motif and lattice
Motif and lattice Sub saharan african city model
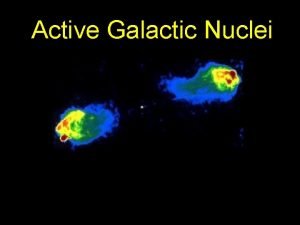
Sub saharan african city model Multiple nuclei model example
Multiple nuclei model example Urban sprawl aphug
Urban sprawl aphug Coliculii cvadrigemeni inferiori
Coliculii cvadrigemeni inferiori Multiple nuclei model ap human geography example
Multiple nuclei model ap human geography example Harris ullman multiple nuclei model
Harris ullman multiple nuclei model Parts of limbic system
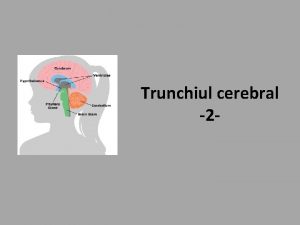
Parts of limbic system Reticular formation
Reticular formation Sanjana bhagwat
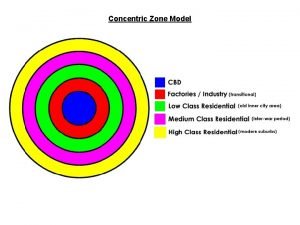
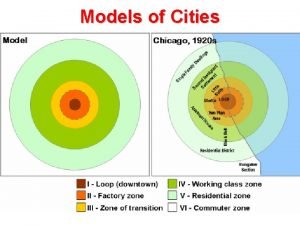
Sanjana bhagwat Concentric zone theory
Concentric zone theory Criticism of concentric zone theory
Criticism of concentric zone theory Tuber cinereum
Tuber cinereum