Active Galactic Nuclei Active Galactic Nuclei AGN Nuclei

Active Galactic Nuclei

Active Galactic Nuclei (AGN) Nuclei of galaxies with peculiar properties: • Extremely bright nuclei • Variability • High-Energy (X-/g-ray) emission • Emission lines • Polarization • Relativistic outflows (jets)

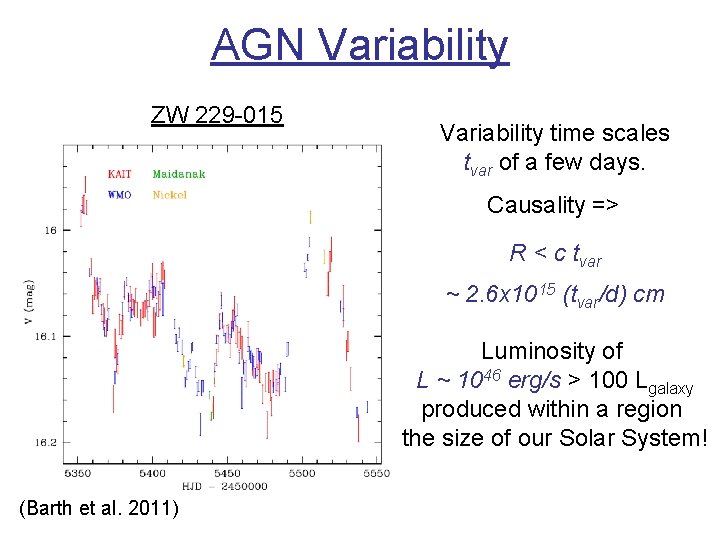
AGN Variability ZW 229 -015 Variability time scales tvar of a few days. Causality => R < c tvar ~ 2. 6 x 1015 (tvar/d) cm Luminosity of L ~ 1046 erg/s > 100 Lgalaxy produced within a region the size of our Solar System! (Barth et al. 2011)

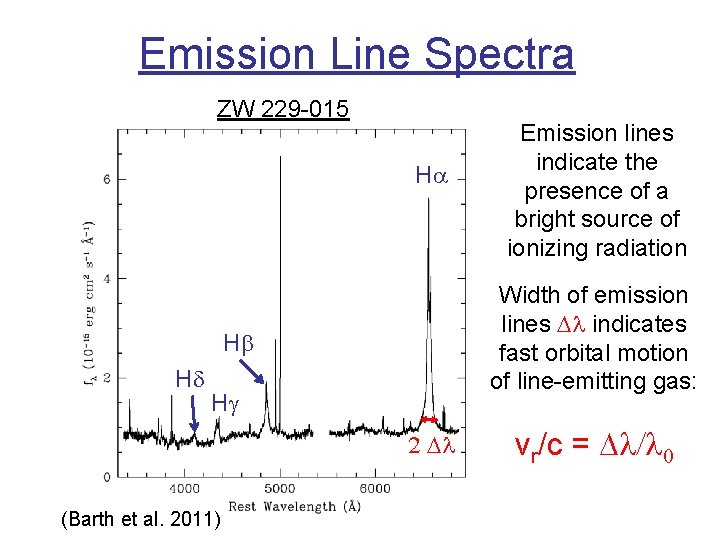
Emission Line Spectra ZW 229 -015 Ha Width of emission lines Dl indicates fast orbital motion of line-emitting gas: Hb Hd Hg 2 Dl (Barth et al. 2011) Emission lines indicate the presence of a bright source of ionizing radiation vr/c = Dl/l 0

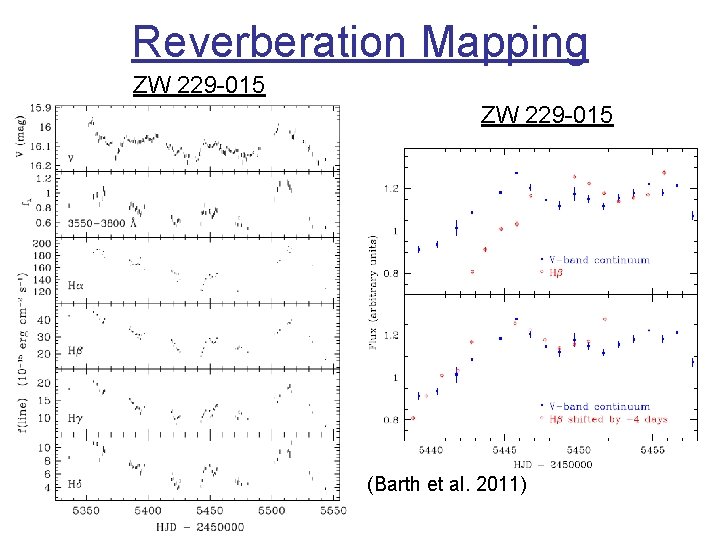
Reverberation Mapping ZW 229 -015 (Barth et al. 2011)

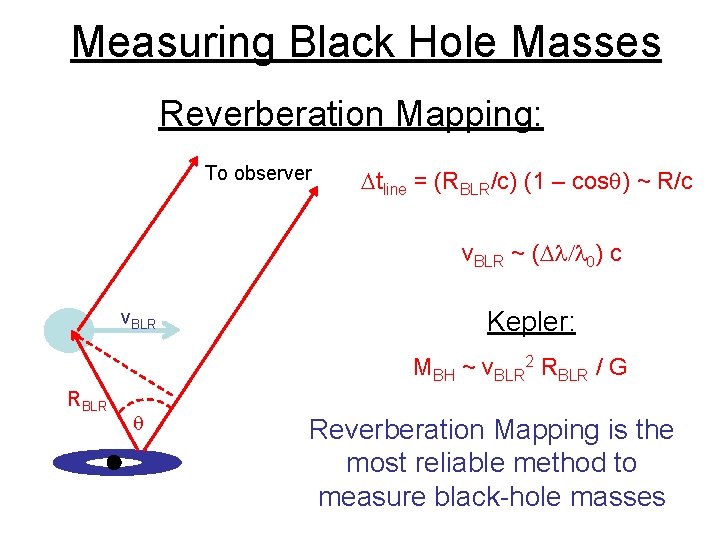
Measuring Black Hole Masses Reverberation Mapping: To observer Dtline = (RBLR/c) (1 – cosq) ~ R/c v. BLR ~ (Dl/l 0) c v. BLR Kepler: MBH ~ v. BLR 2 RBLR / G RBLR q Reverberation Mapping is the most reliable method to measure black-hole masses

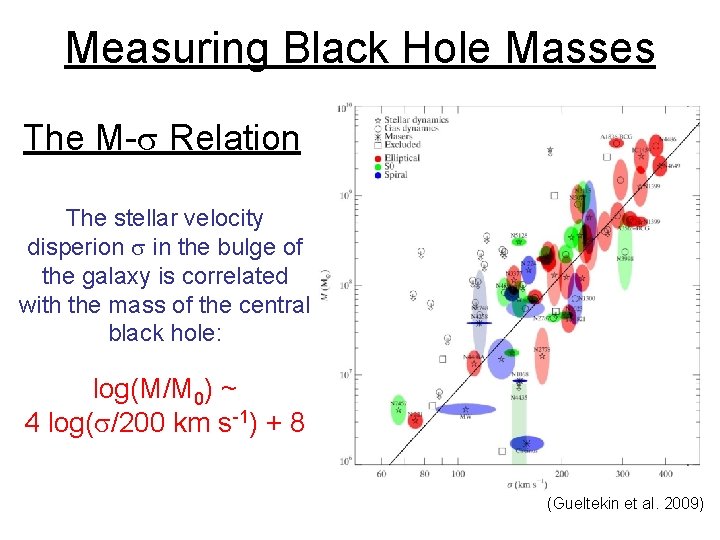
Measuring Black Hole Masses The M-s Relation The stellar velocity disperion s in the bulge of the galaxy is correlated with the mass of the central black hole: log(M/M 0) ~ 4 log(s/200 km s-1) + 8 (Gueltekin et al. 2009)

Cosmic Jets and Radio Lobes Gamma-Rays (Fermi) + Optical Many active galaxies show powerful relativistic jets + Radio Example: Cen A Optical X-rays (Chandra) Optical + Radio

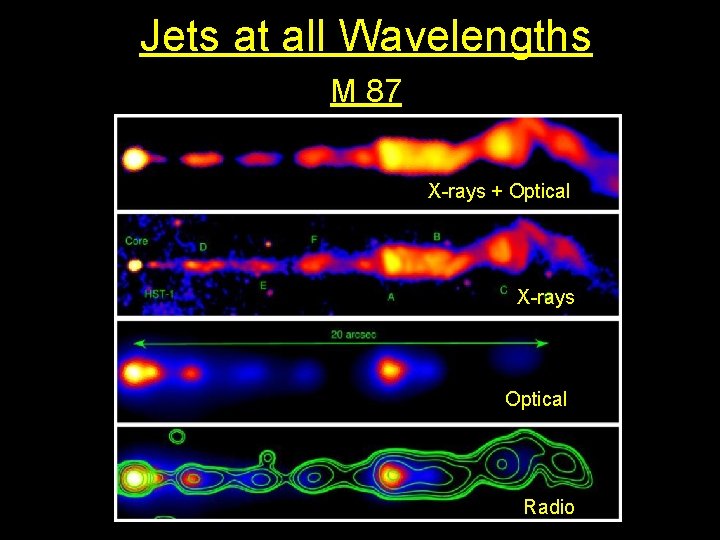
Jets at all Wavelengths M 87 X-rays + Optical X-rays Optical Radio

Evidence for Relativistic Beaming • Fast variability (tvar < 1 d) • High-luminosity (L > 1048 erg/s) Observed in many AGN (blazars) Assuming a stationary source: • Causality => R < c tvar ~ 2. 6*1015 tvar, d cm • R must be larger than the Schwarzschild radius of whatever produces the emission => M < R c 2/(2 G) ~ 8. 7*109 tvar, d M 0 • Luminosity must be smaller than Eddington Limit: => L < 1. 1*1048 tvar, d erg/s Elliot-Shapiro Relation

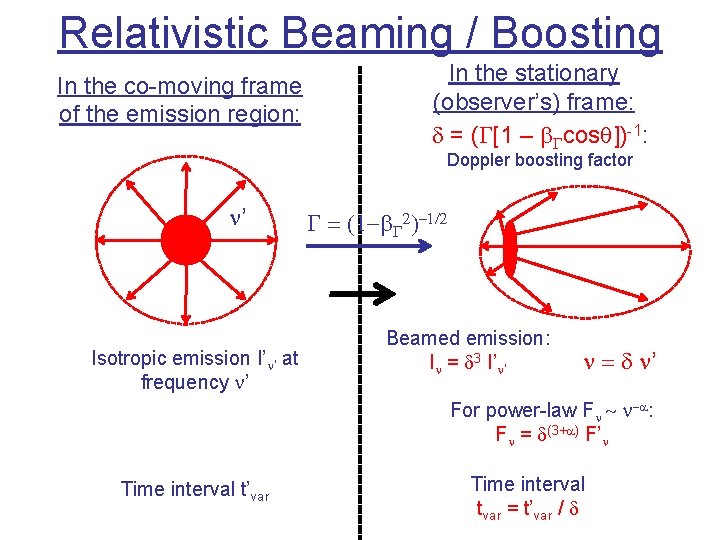
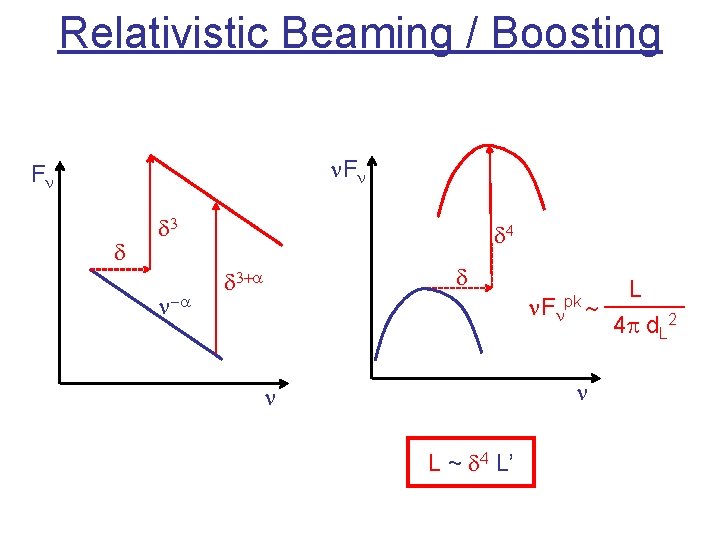
Relativistic Beaming / Boosting In the co-moving frame of the emission region: In the stationary (observer’s) frame: d = (G[1 – b. Gcosq])-1: Doppler boosting factor n’ Isotropic emission I’n’ at frequency n’ G = (1 -b. G 2)-1/2 Beamed emission: In = d 3 I’n’ n = d n’ For power-law Fn ~ n-a: Fn = d(3+a) F’n Time interval t’var Time interval tvar = t’var / d

Relativistic Beaming / Boosting n. Fn Fn d d 3 n-a d 4 d d 3+a n. Fn pk L ______ ~ 4 p d. L 2 n n L ~ d 4 L’

The AGN Zoo Ellipticals Spirals Radio quiet Radio loud Seyferts Radio quiet quasars Radio spectrum Emission lines Broad and narrow Narrow Seyfert 1 Flat Steep Seyfert 2 Blazars Radio galaxies Emission lines Weak/absent Strong BL Lac Objects Steep Spectrum Radio Quasars Flat Spectrum Radio Quasars FR II

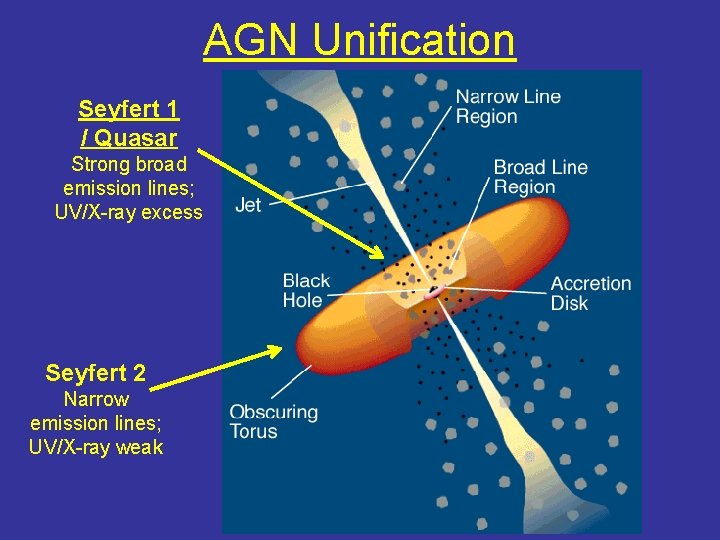
AGN Unification Seyfert 1 / Quasar Strong broad emission lines; UV/X-ray excess Seyfert 2 Narrow emission lines; UV/X-ray weak

Types of radio-loud AGN and AGN Unification n tio c e r i d g in rv e s Ob Cyg A (radio) Radio Galaxy: Powerful radio lobes at the end points of the jets, where kinetic jet power is dissipated.

Types of radio-loud AGN and AGN Unification Flat-Spectrum Radio Quasar or BL Lac object Emission from the jet pointing towards us is Doppler boosted compared to the jet moving in the other direction (“counter jet”). in v er bs O g n io ct re di

Blazars • Class of AGN consisting of BL Lac objects and gamma-ray bright quasars • Rapidly (often intra-day) variable • Strong gamma-ray sources • Radio jets, often with superluminal motion • Radio and optical polarization

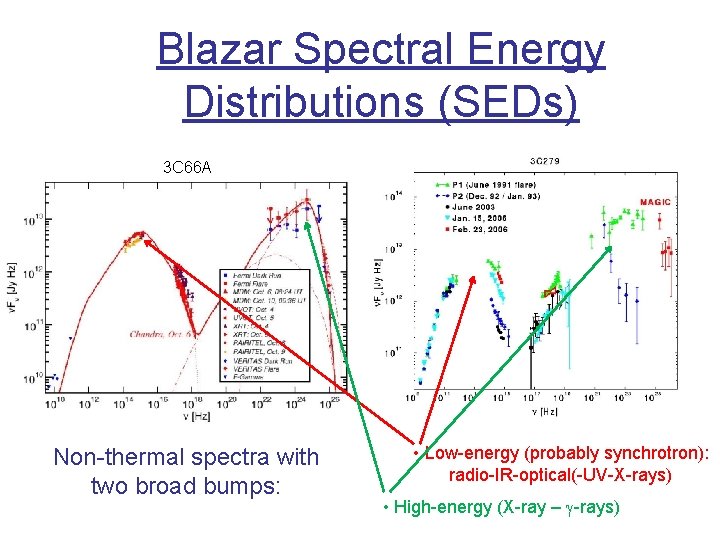
Blazar Spectral Energy Distributions (SEDs) 3 C 66 A Non-thermal spectra with two broad bumps: • Low-energy (probably synchrotron): radio-IR-optical(-UV-X-rays) • High-energy (X-ray – g-rays)

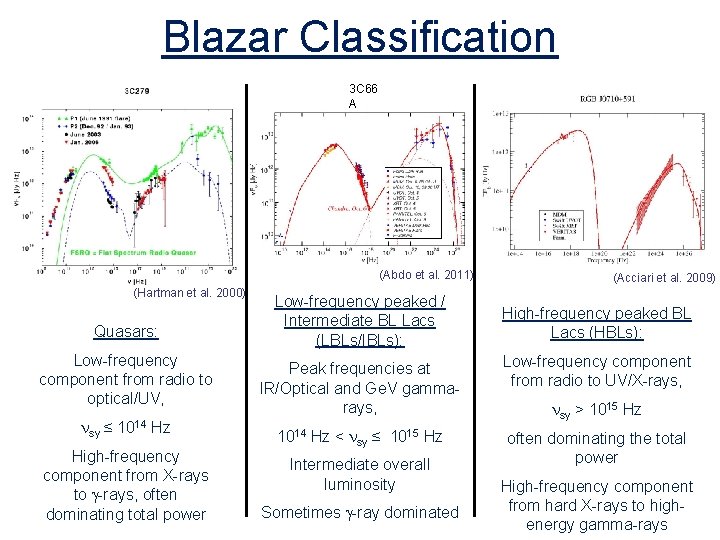
Blazar Classification 3 C 66 A (Abdo et al. 2011) (Hartman et al. 2000) Quasars: Low-frequency component from radio to optical/UV, nsy ≤ 1014 Hz High-frequency component from X-rays to g-rays, often dominating total power Low-frequency peaked / Intermediate BL Lacs (LBLs/IBLs): (Acciari et al. 2009) High-frequency peaked BL Lacs (HBLs): Peak frequencies at IR/Optical and Ge. V gammarays, Low-frequency component from radio to UV/X-rays, 1014 Hz < nsy ≤ 1015 Hz often dominating the total power Intermediate overall luminosity Sometimes g-ray dominated nsy > 1015 Hz High-frequency component from hard X-rays to highenergy gamma-rays

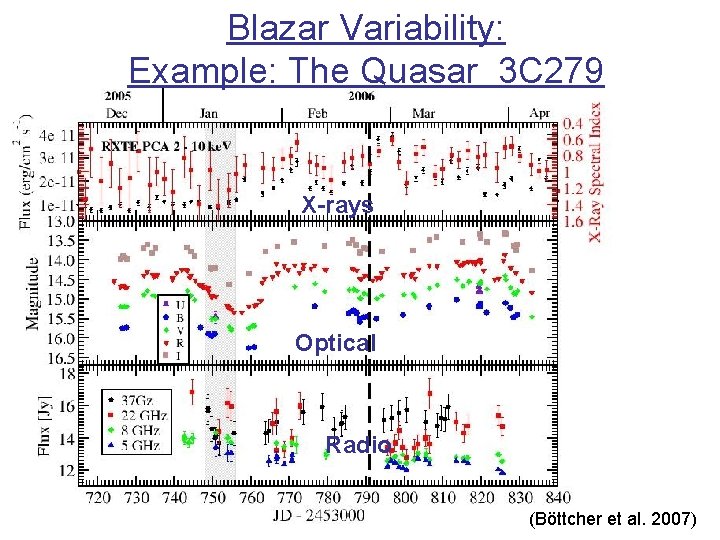
Blazar Variability: Example: The Quasar 3 C 279 X-rays Optical Radio (Bӧttcher et al. 2007)

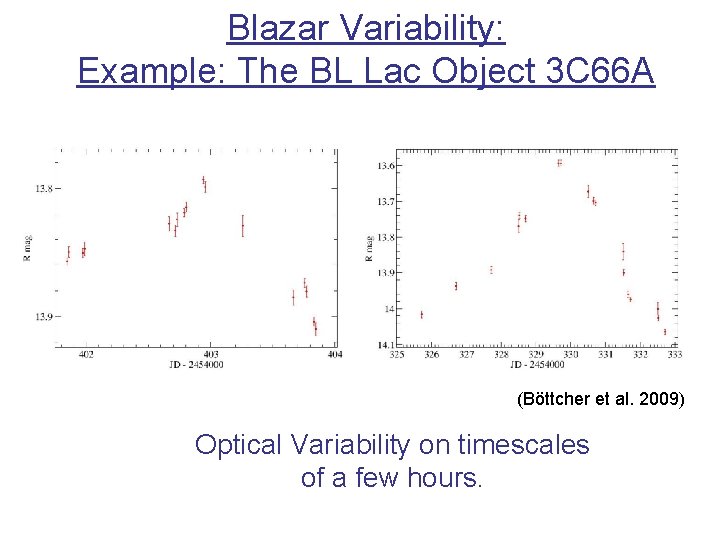
Blazar Variability: Example: The BL Lac Object 3 C 66 A (Bӧttcher et al. 2009) Optical Variability on timescales of a few hours.

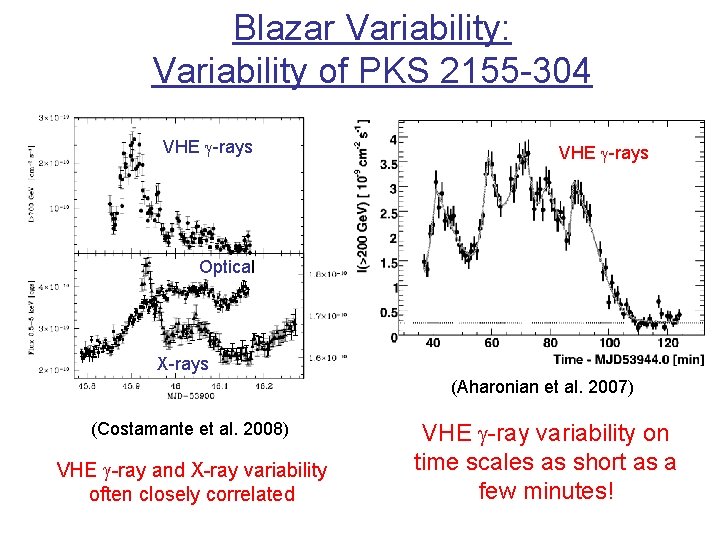
Blazar Variability: Variability of PKS 2155 -304 VHE g-rays Optical X-rays (Aharonian et al. 2007) (Costamante et al. 2008) VHE g-ray and X-ray variability often closely correlated VHE g-ray variability on time scales as short as a few minutes!

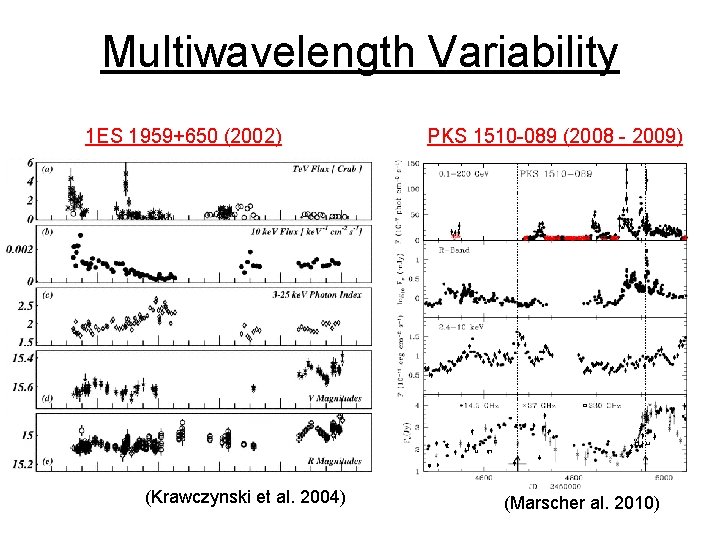
Multiwavelength Variability 1 ES 1959+650 (2002) (Krawczynski et al. 2004) PKS 1510 -089 (2008 - 2009) (Marscher al. 2010)

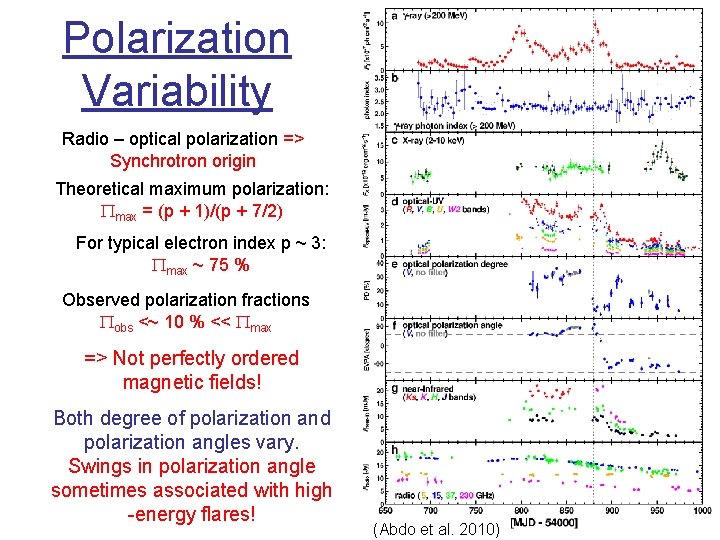
Polarization Variability Radio – optical polarization => Synchrotron origin Theoretical maximum polarization: Pmax = (p + 1)/(p + 7/2) For typical electron index p ~ 3: Pmax ~ 75 % Observed polarization fractions Pobs <~ 10 % << Pmax => Not perfectly ordered magnetic fields! Both degree of polarization and polarization angles vary. Swings in polarization angle sometimes associated with high -energy flares! (Abdo et al. 2010)

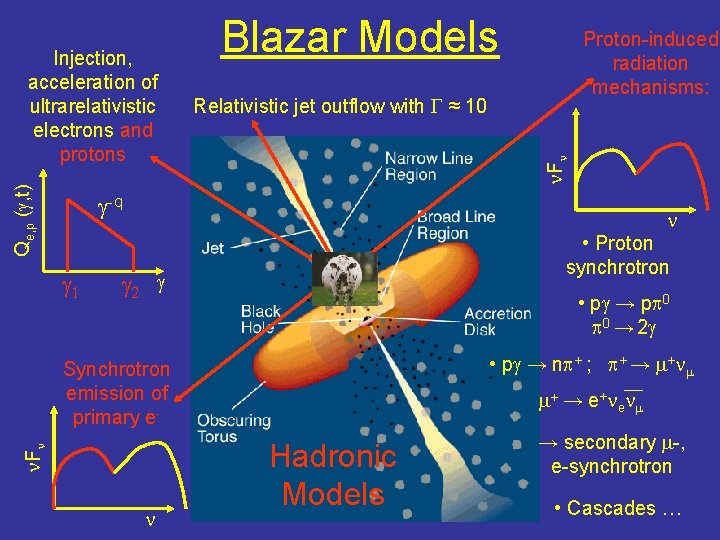
Blazar Models Synchrotron emission Qe (g, t) Injection, acceleration of ultrarelativistic electrons n. Fn Relativistic jet outflow with G ≈ 10 n Compton emission g 1 g 2 g Injection over finite length near the base of the jet. Additional contribution from gg absorption along the jet Leptonic Models n. Fn g-q n Seed photons: Synchrotron (SSC), Accr. Disk + BLR (EC)

Proton-induced radiation mechanisms: Relativistic jet outflow with G ≈ 10 n. Fn Qe, p (g, t) Injection, acceleration of ultrarelativistic electrons and protons Blazar Models g-q g 1 n • Proton synchrotron g 2 g • pg → pp 0 → 2 g • pg → np+ ; p+ → m+nm n. Fn Synchrotron emission of primary e- n m+ → e + n e n m Hadronic Models → secondary m-, e-synchrotron • Cascades …

List of Model Parameters SSC: R: Radius of the emission region G: Bulk Lorentz factor qobs: Observing angle D = (G[1 – b. Gcosq])-1: Doppler boosting factor Linj : Power injected into relativistic electrons g 1: Low-energy cutoff of injected electron spectrum g 2: High-energy cutoff of injected electron spectrum q: Power-law index of injected electron spectrum B: Magnetic field h: Particle escape time scale parameter

Constraints from Observations 1) Variability time scale tvar → Causality => R ≤ c tvar d/(1 + z) → Variability time scales ~ hours => R ≤ 1015 (tvar /hr)(d/10)/(1 + z) cm

Constraints from Observations 2) Superluminal Motion The MOJAVE Project (Lister et al. )

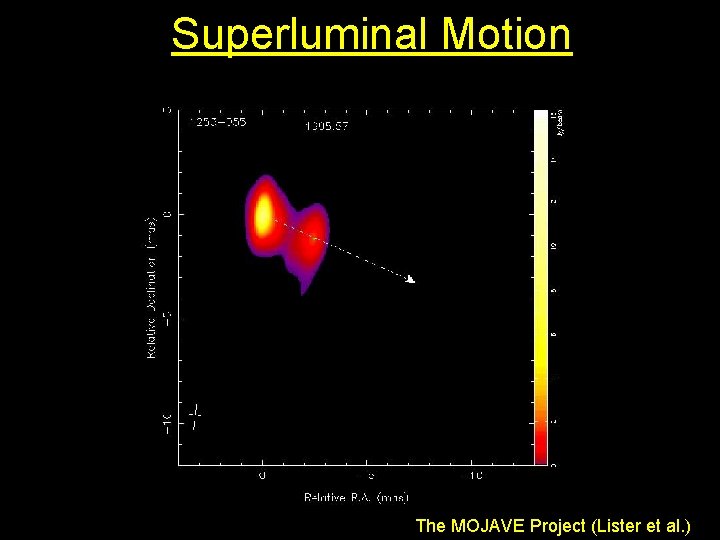
Superluminal Motion The MOJAVE Project (Lister et al. )

Constraints from Observations To observer 2) Superluminal Motion: Dtobs = Dt (1 – b cosq) v , app = v sinq 1 – b cosq G = (1 – b 2)-1/2 b = v/c This is maximum for b = cosq => v Dt sinq max G ≥ 30 at least in some blazars! v Dt cosq b app up to ~ 30 observed Jet b , app = Gb ≈ G q v Dt

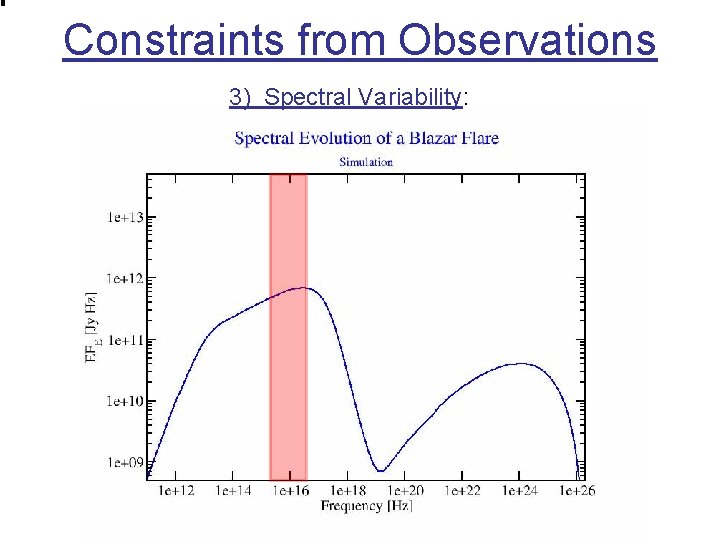
Constraints from Observations 3) Spectral Variability:

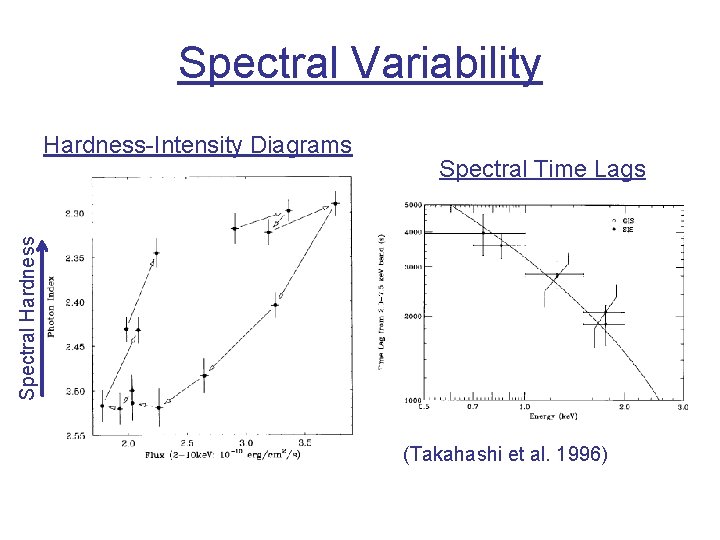
Spectral Variability Spectral Time Lags Spectral Hardness-Intensity Diagrams (Takahashi et al. 1996)

Constraints from Observations 3) Spectral Variability: If energy-dependent (spectral) time lags are related to energy-dependent synchrotron cooling time scale: dg/dt = -n 0 g 2 with n 0 = (4/3) c s. T u’B tcool = g/|dg/dt| = 1/(n 0 g) and nsy = 3. 4*106 (B/G) (d/(1+z)) g 2 Hz => Dtcool ~ B-3/2 (d/(1+z))1/2 (n 1 -1/2 – n 2 -1/2) => Measure time lags between frequencies n 1, n 2 → estimate Magnetic field (modulo d/[1+z])!

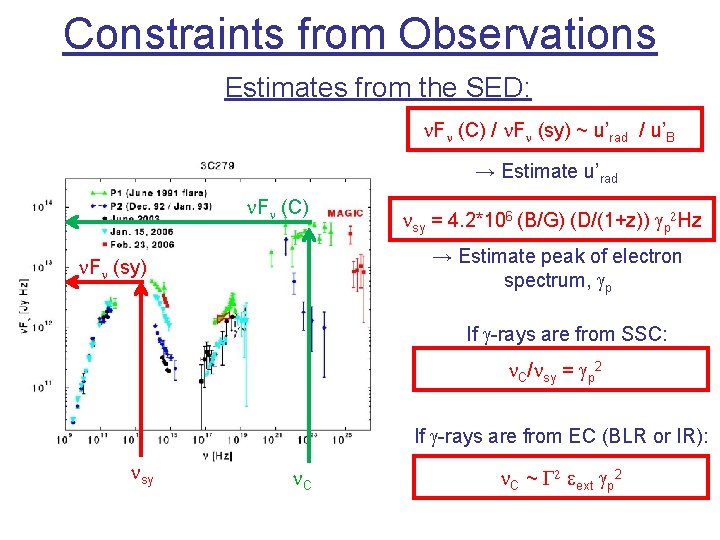
Constraints from Observations Estimates from the SED: n. Fn (C) / n. Fn (sy) ~ u’rad / u’B → Estimate u’rad n. Fn (C) nsy = 4. 2*106 (B/G) (D/(1+z)) gp 2 Hz → Estimate peak of electron spectrum, gp n. Fn (sy) If g-rays are from SSC: n. C/nsy = gp 2 If g-rays are from EC (BLR or IR): nsy n. C ~ G 2 eext gp 2

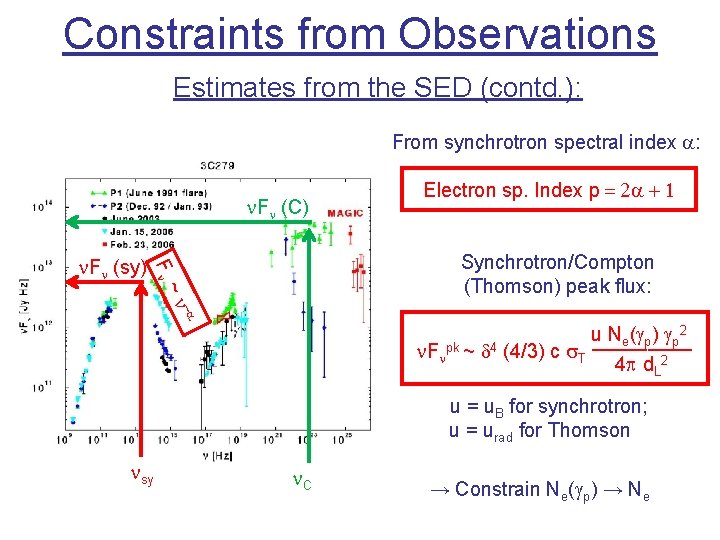
Constraints from Observations Estimates from the SED (contd. ): From synchrotron spectral index a: n. Fn (C) Synchrotron/Compton (Thomson) peak flux: Fn n. Fn (sy) Electron sp. Index p = 2 a + 1 -a ~n u Ne(gp) gp 2 _____ n. Fnpk ~ d 4 (4/3) c s. T 4 p d. L 2 u = u. B for synchrotron; u = urad for Thomson nsy n. C → Constrain Ne(gp) → Ne