FractionalSuperstring Amplitudes from the MultiCut Matrix Models Hirotaka

![Collaborators of [CISY]: [CISY 1] “Macroscopic loop amplitudes in the multi-cut two-matrix models”, Nucl. Collaborators of [CISY]: [CISY 1] “Macroscopic loop amplitudes in the multi-cut two-matrix models”, Nucl.](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-2.jpg)

![A brief summary for multi-comp. KP hierarchy Claim [Fukuma-HI ‘ 06] the orthonormal polynomial A brief summary for multi-comp. KP hierarchy Claim [Fukuma-HI ‘ 06] the orthonormal polynomial](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-9.jpg)

![Various notes [CISY 1 ‘ 09] e. g. ) (2, 2) 3 -cut critical Various notes [CISY 1 ‘ 09] e. g. ) (2, 2) 3 -cut critical](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-11.jpg)
![Various notes [CISY 1 ‘ 09] The operators A and B are given by Various notes [CISY 1 ‘ 09] The operators A and B are given by](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-12.jpg)

![Various notes [CISY 1 ‘ 09] The operators A and B are given by Various notes [CISY 1 ‘ 09] The operators A and B are given by](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-14.jpg)

![What should correspond to the multi-cut matrix models? [HI ‘ 09] Reconsider the TWO-cut What should correspond to the multi-cut matrix models? [HI ‘ 09] Reconsider the TWO-cut](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-16.jpg)
![What should correspond to the multi-cut matrix models? [HI ‘ 09] How about MULTI What should correspond to the multi-cut matrix models? [HI ‘ 09] How about MULTI](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-17.jpg)
![Which ψ ? [HI ‘ 09] Zamolodchikov-Fateev parafermion [Zamolodchikov-Fateev ‘ 85] 1. Basic parafermion Which ψ ? [HI ‘ 09] Zamolodchikov-Fateev parafermion [Zamolodchikov-Fateev ‘ 85] 1. Basic parafermion](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-18.jpg)
![Correspondence [HI ‘ 09] (p, q) Minimal k-fractional superstrings Z_k symmetric case: This means Correspondence [HI ‘ 09] (p, q) Minimal k-fractional superstrings Z_k symmetric case: This means](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-19.jpg)
![Summary of Evidences and Issues [HI ‘ 09] ü Labeling of critical points (p, Summary of Evidences and Issues [HI ‘ 09] ü Labeling of critical points (p,](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-20.jpg)


![The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] : Orthogonal polynomial [Gross-Migdal ‘ 90] The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] : Orthogonal polynomial [Gross-Migdal ‘ 90]](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-23.jpg)
![The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] Solve this system in the week The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] Solve this system in the week](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-24.jpg)
![The k-Cut extension [CISY 1 ‘ 09] Solve this system in the week coupling The k-Cut extension [CISY 1 ‘ 09] Solve this system in the week coupling](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-25.jpg)

![Our Ansatz: [CISY 1 ‘ 09] The EZJ-DKK eq. gives several polynomials… Our Ansatz: [CISY 1 ‘ 09] The EZJ-DKK eq. gives several polynomials…](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-27.jpg)
![(k, l)=(3, 1) cases [CISY 1 ‘ 09] We identify are the Jacobi Polynomial (k, l)=(3, 1) cases [CISY 1 ‘ 09] We identify are the Jacobi Polynomial](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-28.jpg)
![Our Solution: [CISY 1 ‘ 09] Jacobi polynomials Our ansatz is applicable to every Our Solution: [CISY 1 ‘ 09] Jacobi polynomials Our ansatz is applicable to every](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-29.jpg)
![Geometry [CISY 1 ‘ 09] (1, 1) critical point (l=1): (1, 1) critical point Geometry [CISY 1 ‘ 09] (1, 1) critical point (l=1): (1, 1) critical point](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-30.jpg)

![Z_k breaking cases: [CISY 2 ‘ 09] Solve this system in the week coupling Z_k breaking cases: [CISY 2 ‘ 09] Solve this system in the week coupling](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-32.jpg)

![The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-34.jpg)
![The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-35.jpg)
![The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09] The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09]](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-36.jpg)
![The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09] The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09]](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-38.jpg)
![Algebraic Equations [CISY 2 ‘ 09] The cosh solution: The sinh solution: Here, (p, Algebraic Equations [CISY 2 ‘ 09] The cosh solution: The sinh solution: Here, (p,](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-39.jpg)
![An Example of Algebraic Curves (k=4) [CISY 2 ‘ 09] COSH (µ<0) SINH (µ>0) An Example of Algebraic Curves (k=4) [CISY 2 ‘ 09] COSH (µ<0) SINH (µ>0)](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-40.jpg)
![Conclusion of Z_k breaking cases: [CISY 2 ‘ 09] 1. We gave the solution Conclusion of Z_k breaking cases: [CISY 2 ‘ 09] 1. We gave the solution](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-41.jpg)

- Slides: 42

Fractional-Superstring Amplitudes from the Multi-Cut Matrix Models Hirotaka Irie (National Taiwan University, Taiwan) 20 Dec. 2009 @ Taiwan String Workshop 2010 Ref) HI, “Fractional supersymmetric Liouville theory and the multi-cut matrix models”, Nucl. Phys. B 819 [PM] (2009) 351 CT-Chan, HI, SY-Shih and CH-Yeh, “Macroscopic loop amplitudes in the multi-cut two-matrix models, ” Nucl. Phys. B (10. 1016/j. nuclphysb. 2009. 10. 017), in press CT-Chan, HI, SY-Shih and CH-Yeh, “Fractional-superstring amplitudes from the multi-cut two-matrix models (tentative), ” ar. Xiv: 0912. ****, in preparation.
![Collaborators of CISY CISY 1 Macroscopic loop amplitudes in the multicut twomatrix models Nucl Collaborators of [CISY]: [CISY 1] “Macroscopic loop amplitudes in the multi-cut two-matrix models”, Nucl.](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-2.jpg)
Collaborators of [CISY]: [CISY 1] “Macroscopic loop amplitudes in the multi-cut two-matrix models”, Nucl. Phys. B (10. 1016/j. nuclphysb. 2009. 10. 017) [CISY 2] “Fractional-superstring amplitudes from the multi-cut twomatrix models”, ar. Xiv: 0912. ****, in preparation Chuan-Tsung Chan (Tunghai University, Taiwan) Sheng-Yu Darren Shih (NTU, Taiwan UC, Berkeley, US [Sept. 1 ~]) Chi-Hsien Yeh (NTU, Taiwan)

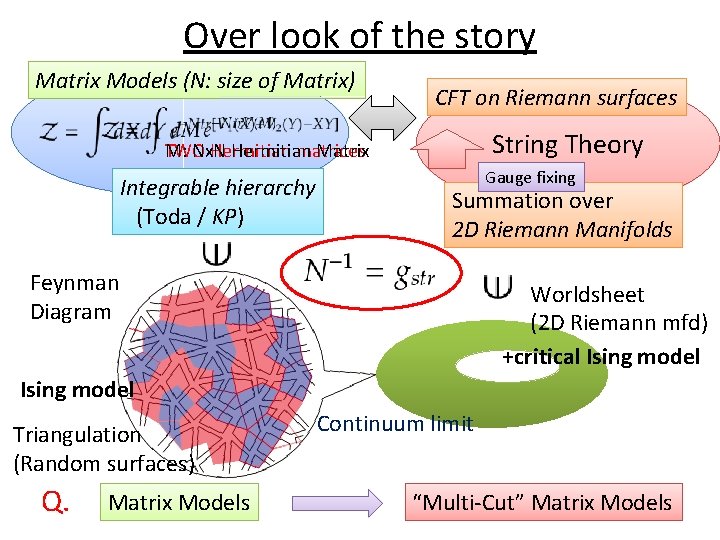
Over look of the story Matrix Models (N: size of Matrix) CFT on Riemann surfaces String Theory M: TWO Nx. N Hermitian matrices Matrix Integrable hierarchy (Toda / KP) Gauge fixing Summation over 2 D Riemann Manifolds Feynman Diagram Worldsheet (2 D Riemann mfd) +critical Ising model Triangulation (Random surfaces) Q. Matrix Models Continuum limit “Multi-Cut” Matrix Models

1. What is the multi-cut matrix models? 2. What should correspond to the multicut matrix models? 3. Macroscopic Loop Amplitudes 4. Fractional-Superstring Amplitudes from the Multi-Cut Matrix Models

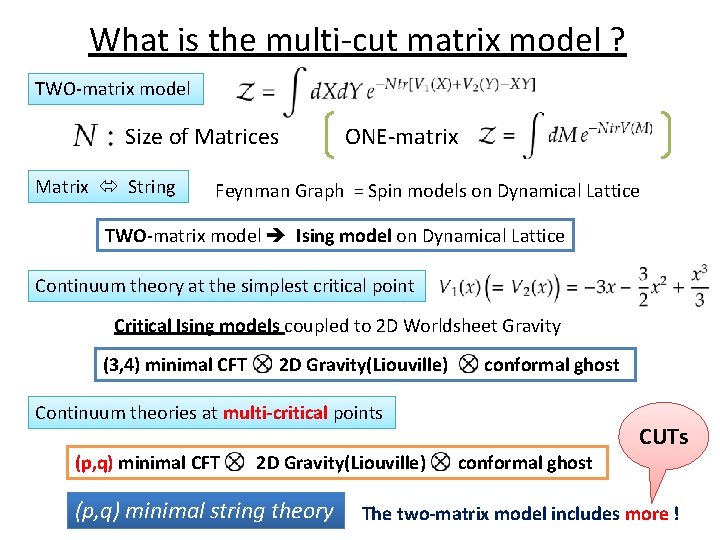
What is the multi-cut matrix model ? TWO-matrix model Size of Matrices Matrix String ONE-matrix Feynman Graph = Spin models on Dynamical Lattice TWO-matrix model Ising model on Dynamical Lattice Continuum theory at the simplest critical point Critical Ising models coupled to 2 D Worldsheet Gravity (3, 4) minimal CFT 2 D Gravity(Liouville) conformal ghost Continuum theories at multi-critical points (p, q) minimal CFT 2 D Gravity(Liouville) (p, q) minimal string theory conformal ghost CUTs The two-matrix model includes more !

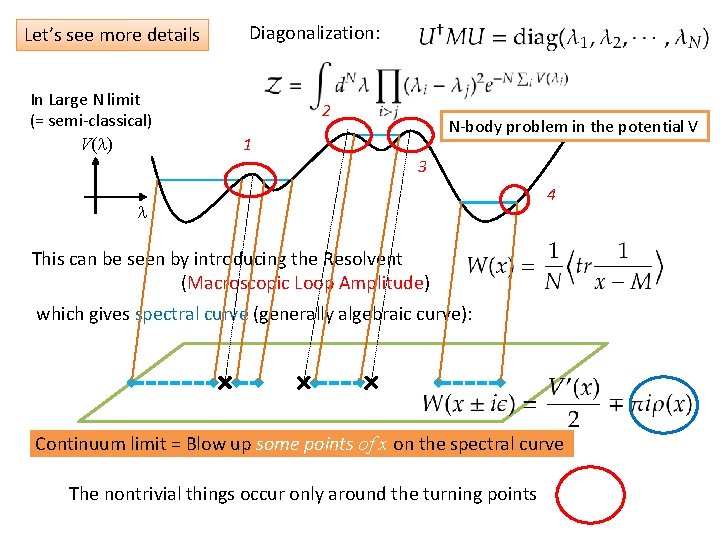
Let’s see more details In Large N limit (= semi-classical) V(l) Diagonalization: 2 N-body problem in the potential V 1 3 l 4 This can be seen by introducing the Resolvent (Macroscopic Loop Amplitude) which gives spectral curve (generally algebraic curve): Continuum limit = Blow up some points of x on the spectral curve The nontrivial things occur only around the turning points

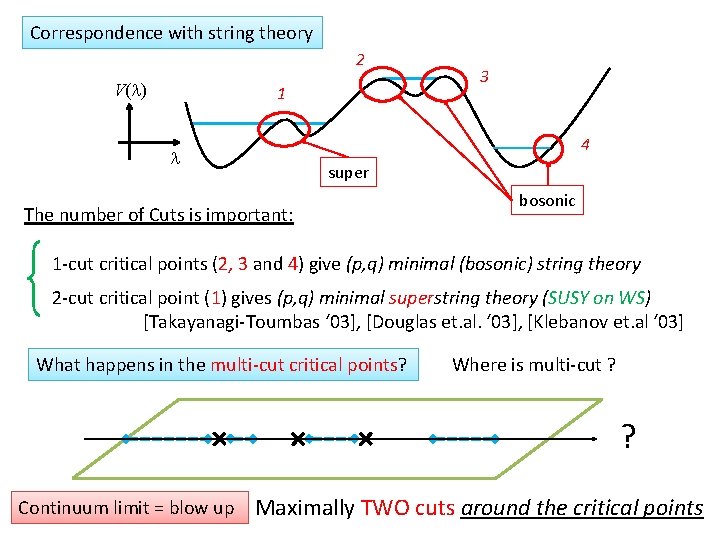
Correspondence with string theory 2 V(l) 1 3 4 l super The number of Cuts is important: bosonic 1 -cut critical points (2, 3 and 4) give (p, q) minimal (bosonic) string theory 2 -cut critical point (1) gives (p, q) minimal superstring theory (SUSY on WS) [Takayanagi-Toumbas ‘ 03], [Douglas et. al. ‘ 03], [Klebanov et. al ‘ 03] What happens in the multi-cut critical points? Where is multi-cut ? ? Continuum limit = blow up Maximally TWO cuts around the critical points

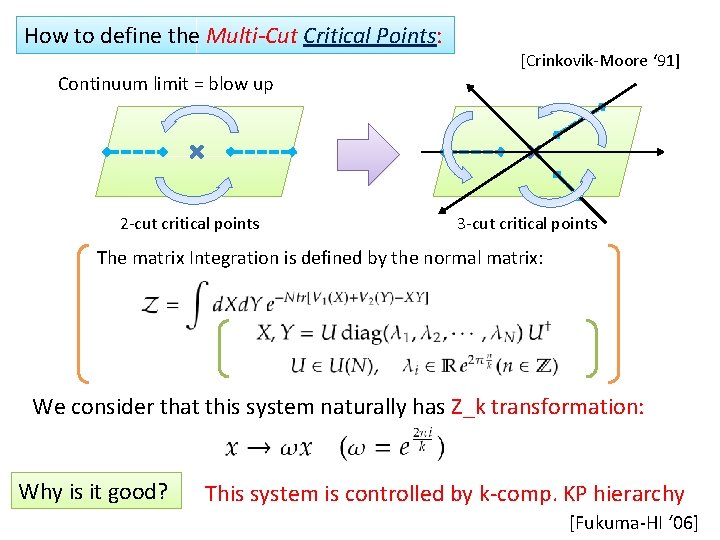
How to define the Multi-Cut Critical Points: Continuum limit = blow up 2 -cut critical points [Crinkovik-Moore ‘ 91] 3 -cut critical points The matrix Integration is defined by the normal matrix: We consider that this system naturally has Z_k transformation: Why is it good? This system is controlled by k-comp. KP hierarchy [Fukuma-HI ‘ 06]
![A brief summary for multicomp KP hierarchy Claim FukumaHI 06 the orthonormal polynomial A brief summary for multi-comp. KP hierarchy Claim [Fukuma-HI ‘ 06] the orthonormal polynomial](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-9.jpg)
A brief summary for multi-comp. KP hierarchy Claim [Fukuma-HI ‘ 06] the orthonormal polynomial system of the matrix model: Derives the Baker-Akiehzer function system of k-comp. KP hierarchy Recursive relations: Infinitely many Integrable deformation Toda hierarchy Lax operators k-component KP hierarchy k x k Matrix-Valued Differential Operators 1. Index Shift Op. -> Index derivative Op. At critical points (continuum limit): Continuum function of “n”

2. The Z_k symmetry: k distinct orthonormal polynomials at the origin: somehow k distinct smooth continuum functions at the origin: Smooth function in x and l The relation between α and f: [Crinkovik-Moore ‘ 91](ONE), [CISY 1 ‘ 09](TWO) Labeling of distinct scaling functions k-component KP hierarchy with Z_k symmetry symmetric breaking cases: Summary: 1. What happens in multi-cut matrix models? 2. Multi-cut matrix models k-component KP hierarchy 3. We are going to give several notes
![Various notes CISY 1 09 e g 2 2 3 cut critical Various notes [CISY 1 ‘ 09] e. g. ) (2, 2) 3 -cut critical](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-11.jpg)
Various notes [CISY 1 ‘ 09] e. g. ) (2, 2) 3 -cut critical point [CISY 1 ‘ 09] Critical potential Blue = lower / yellow = higher
![Various notes CISY 1 09 The operators A and B are given by Various notes [CISY 1 ‘ 09] The operators A and B are given by](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-12.jpg)
Various notes [CISY 1 ‘ 09] The operators A and B are given by 1. The coefficient matrices are all REAL 2. The Z_k symmetric critical points are given by ( : the shift matrix)

The Z_k symmetric cases can be restricted to
![Various notes CISY 1 09 The operators A and B are given by Various notes [CISY 1 ‘ 09] The operators A and B are given by](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-14.jpg)
Various notes [CISY 1 ‘ 09] The operators A and B are given by 1. The coefficient matrices are all REAL functions 2. The Z_k symmetric critical points are given by ( : the shift matrix) 3. We can also break Z_k symmetry (difference from Z_k symmetric cases)

1. What is the multi-cut matrix models? 2. What should correspond to the multicut matrix models? 3. Macroscopic Loop Amplitudes 4. Fractional-Superstring Amplitudes from the Multi-Cut Matrix Models
![What should correspond to the multicut matrix models HI 09 Reconsider the TWOcut What should correspond to the multi-cut matrix models? [HI ‘ 09] Reconsider the TWO-cut](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-16.jpg)
What should correspond to the multi-cut matrix models? [HI ‘ 09] Reconsider the TWO-cut cases: Z_2 transformation = (Z_2) R-R charge conjugation [Takayanagi-Toumbas ‘ 03], [Douglas et. al. ‘ 03], [Klebanov et. al ‘ 03] Neveu-Shwartz sector: 2 -cut critical points Because of WS Fermion Ramond sector: Z_2 spin structure => Selection rule => Charge ONE-cut: TWO-cut: Gauge it away by superconformal symmetry Superstrings !
![What should correspond to the multicut matrix models HI 09 How about MULTI What should correspond to the multi-cut matrix models? [HI ‘ 09] How about MULTI](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-17.jpg)
What should correspond to the multi-cut matrix models? [HI ‘ 09] How about MULTI (=k) -cut cases: [HI ‘ 09] Z_k transformation =? = Z_k “R-R charge” conjugation 3 -cut critical points Because of “Generalized Fermion” R 0 (= NS) sector: Rn sector: Z_k spin structure => Selection rule => Charge ONE-cut: multi-cut: Gauge it away by Generalized superconformal symmetry
![Which ψ HI 09 ZamolodchikovFateev parafermion ZamolodchikovFateev 85 1 Basic parafermion Which ψ ? [HI ‘ 09] Zamolodchikov-Fateev parafermion [Zamolodchikov-Fateev ‘ 85] 1. Basic parafermion](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-18.jpg)
Which ψ ? [HI ‘ 09] Zamolodchikov-Fateev parafermion [Zamolodchikov-Fateev ‘ 85] 1. Basic parafermion fields: 2. Central charge: 3. The OPE algebra: k parafermion fields: Z_k spin-fields: 4. The symmetry and its minimal models of : k-Fractional superconformal sym. GKO construction Minimal k-fractional super-CFT: (k=1: bosonic (l+2, l+3), k=2: super (l+2, l+4)) Why is it good? It is because the spectrums of the (p, q) minimal fractional super-CFT and the multi-cut matrix models [HI ‘ 09] are the same.
![Correspondence HI 09 p q Minimal kfractional superstrings Zk symmetric case This means Correspondence [HI ‘ 09] (p, q) Minimal k-fractional superstrings Z_k symmetric case: This means](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-19.jpg)
Correspondence [HI ‘ 09] (p, q) Minimal k-fractional superstrings Z_k symmetric case: This means that Z_k symmetry is broken (at least to Z_2) ! Minimal k-fractional super-CFT requires Screening charge: : R 2 sector Z_k sym is broken : R(k-2) sector (at least to Z_2) !
![Summary of Evidences and Issues HI 09 ü Labeling of critical points p Summary of Evidences and Issues [HI ‘ 09] ü Labeling of critical points (p,](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-20.jpg)
Summary of Evidences and Issues [HI ‘ 09] ü Labeling of critical points (p, q) and Operator contents (ASSUME: OP of minimal CFT and minimal strings are 1 to 1) ü Residual symmetry On both sectors, the Z_k symmetry broken or to Z_2. ü String susceptibility (of cosmological constant) Q 1 p Fractional supersymmetric Ghost system bc ghost + “ghost chiral parafermion” ? Q 2 p Covariant quantization / BRST Cohomology Complete proof of operator correspondence Q 3 p Correlators (D-brane amplitudes / macroscopic loop amplitudes) Ghost might be factorized (we can compare Matrix/CFT !) Let’s consider macroscopic loop amplitudes !!

1. What is the multi-cut matrix models? 2. What should correspond to the multicut matrix models? 3. Macroscopic Loop Amplitudes 4. Fractional-Superstring Amplitudes from the Multi-Cut Matrix Models

Macroscopic Loop Amplitudes Role of Macroscopic loop amplitudes 1. 2. 3. 4. Eigenvalue density Generating function of On-shell Vertex Op: FZZT-brane disk amplitudes (Comparison to String Theory) D-Instanton amplitudes also come from this amplitude 1 -cut general (p, q) critical point: [Kostov ‘ 90] Off critical perturbation : the Chebyshev Polynomial of the 1 st kind 2 -cut general (p, q) critical point: [Seiberg-Shih ‘ 03] (from Liouville theory) : the Chebyshev Polynomial of the 2 nd kind
![The DaulKazakovKostov prescription 1 cut DKK 93 Orthogonal polynomial GrossMigdal 90 The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] : Orthogonal polynomial [Gross-Migdal ‘ 90]](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-23.jpg)
The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] : Orthogonal polynomial [Gross-Migdal ‘ 90] Solve this system in the week coupling limit Solve thisk-comp. system. KP at hierarchy) the large N limit (Dispersionless More precisely [DKK ‘ 93]
![The DaulKazakovKostov prescription 1 cut DKK 93 Solve this system in the week The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] Solve this system in the week](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-24.jpg)
The Daul-Kazakov-Kostov prescription (1 -cut) [DKK ‘ 93] Solve this system in the week coupling limit (Dispersionless k-componet KP hierarchy) Dimensionless valuable: Scaling Eynard-Zinn-Justin-Daul-Kazakov-Kostov eq. Addition formula of trigonometric functions (q=p+1: Unitary series)
![The kCut extension CISY 1 09 Solve this system in the week coupling The k-Cut extension [CISY 1 ‘ 09] Solve this system in the week coupling](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-25.jpg)
The k-Cut extension [CISY 1 ‘ 09] Solve this system in the week coupling limit The coefficients and are k x k matrices 1. The 0 -th order: : Simultaneous diagonalization 2. The next order: (eigenvalues: j=1, 2, … , k ) EZJ-DKK eq. they are no longer polynomials in general the Z_k symmetric case:

The Z_k symmetric cases can be restricted to We can easily solve the diagonalization problem !
![Our Ansatz CISY 1 09 The EZJDKK eq gives several polynomials Our Ansatz: [CISY 1 ‘ 09] The EZJ-DKK eq. gives several polynomials…](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-27.jpg)
Our Ansatz: [CISY 1 ‘ 09] The EZJ-DKK eq. gives several polynomials…
![k l3 1 cases CISY 1 09 We identify are the Jacobi Polynomial (k, l)=(3, 1) cases [CISY 1 ‘ 09] We identify are the Jacobi Polynomial](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-28.jpg)
(k, l)=(3, 1) cases [CISY 1 ‘ 09] We identify are the Jacobi Polynomial
![Our Solution CISY 1 09 Jacobi polynomials Our ansatz is applicable to every Our Solution: [CISY 1 ‘ 09] Jacobi polynomials Our ansatz is applicable to every](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-29.jpg)
Our Solution: [CISY 1 ‘ 09] Jacobi polynomials Our ansatz is applicable to every k (=3, 4, …) cut cases !! : 1 st Chebyshev : 2 nd Chebyshev
![Geometry CISY 1 09 1 1 critical point l1 1 1 critical point Geometry [CISY 1 ‘ 09] (1, 1) critical point (l=1): (1, 1) critical point](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-30.jpg)
Geometry [CISY 1 ‘ 09] (1, 1) critical point (l=1): (1, 1) critical point (l=0):

1. What is the multi-cut matrix models? 2. What should correspond to the multicut matrix models? 3. Macroscopic Loop Amplitudes 4. Fractional-Superstring Amplitudes from the Multi-Cut Matrix Models
![Zk breaking cases CISY 2 09 Solve this system in the week coupling Z_k breaking cases: [CISY 2 ‘ 09] Solve this system in the week coupling](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-32.jpg)
Z_k breaking cases: [CISY 2 ‘ 09] Solve this system in the week coupling limit The coefficients and are k x k matrices 1. The 0 -th order: Simultaneous diagonalization 2. The next order: (eigenvalues: j=1, 2, … , k ) EZJ-DKK eq. they are no longer polynomials in general Z_k symmetry breaking cases:

The Z_k symmetry breaking cases have general distributions How do we do diagonalization ? We made a jump!
![The general kcut p q solution CISY 2 09 1 The COSH solution The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-34.jpg)
The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution (k is odd and even): 2. The SINH solution (k is even): The deformed Chebyshev functions are solution to EZJ-DKK equation:
![The general kcut p q solution CISY 2 09 1 The COSH solution The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-35.jpg)
The general k-cut (p, q) solution: [CISY 2 ‘ 09] 1. The COSH solution (k is odd and even): 2. The SINH solution (k is even): The characteristic equation: Algebraic equation of (ζ, z) Coeff. are all real functions
![The matrix realization for the every p q k solution CISY 2 09 The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09]](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-36.jpg)
The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09] With a replacement: Repeatedly using the addition formulae, we can show for every pair of (p, q) !

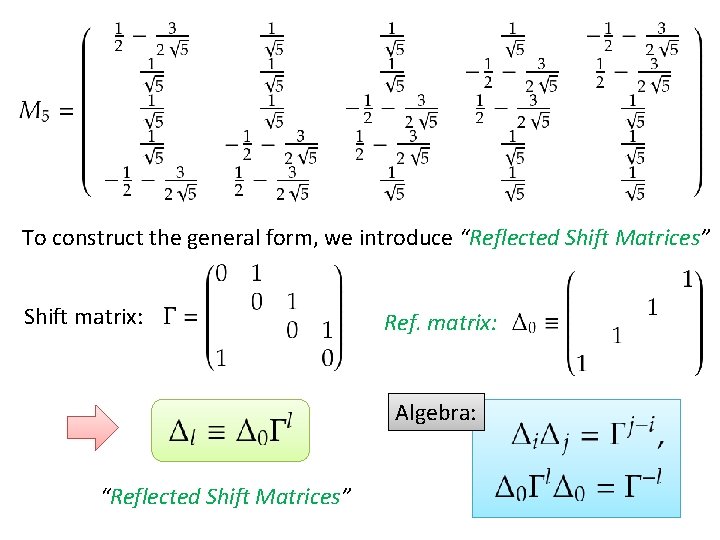
To construct the general form, we introduce “Reflected Shift Matrices” Shift matrix: Ref. matrix: Algebra: “Reflected Shift Matrices”
![The matrix realization for the every p q k solution CISY 2 09 The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09]](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-38.jpg)
The matrix realization for the every (p, q; k) solution [CISY 2 ‘ 09] In this formula we define: A matrix realization for the COSH solution (p, q; k): A matrix realization for the SINH solution (p, q; k), (k is even): The other realizations are related by some proper siminality tr.
![Algebraic Equations CISY 2 09 The cosh solution The sinh solution Here p Algebraic Equations [CISY 2 ‘ 09] The cosh solution: The sinh solution: Here, (p,](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-39.jpg)
Algebraic Equations [CISY 2 ‘ 09] The cosh solution: The sinh solution: Here, (p, q) is CFT labeling !!! Multi-Cut Matrix Model knows (p, q) Minimal Fractional String!
![An Example of Algebraic Curves k4 CISY 2 09 COSH µ0 SINH µ0 An Example of Algebraic Curves (k=4) [CISY 2 ‘ 09] COSH (µ<0) SINH (µ>0)](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-40.jpg)
An Example of Algebraic Curves (k=4) [CISY 2 ‘ 09] COSH (µ<0) SINH (µ>0) : Z_2 charge conjugation (k=2) is equivalent to η=-1 brane of type 0 minimal superstrings k=4 MFSST (k=2) MSST with η=± 1 ? ?
![Conclusion of Zk breaking cases CISY 2 09 1 We gave the solution Conclusion of Z_k breaking cases: [CISY 2 ‘ 09] 1. We gave the solution](https://slidetodoc.com/presentation_image_h2/8732f9c615d8152ef05bd4c70c4bbdf4/image-41.jpg)
Conclusion of Z_k breaking cases: [CISY 2 ‘ 09] 1. We gave the solution to the general k-cut (p, q) Z_k breaking critical points. 2. They are cosh/sinh solutions. We showed all the cases have the matrix realizations. 3. Only the cosh/sinh solutions have the characteristic equations which are algebraic equations with real coefficients. (The other phase shifts are not allowed. ) 4. This includes the ONE-cut and TWO-cut cases. The (p, q) CFT labeling naturally appears! The cosh/sinh indicates the Modular S-matrix of the CFT.

Some of Future Issues 1. Now it’s time to calculate the boundary states of fractional super-Liouville field theory ! 2. What is “fractional super-Riemann surfaces”? 3. Which string theory corresponds to the Z_k symmetric critical points (the Jacobi-poly. sol. ) ? [CISY 1’ 09] 4. Annulus amplitudes ? (Sym, Asym) 5. k=4 MFSST (k=2) MSST with η=± 1 (cf. [HI’ 07]) The Multi-Cut Matrix Models May Include Many New Interesting Phenomena !!!
 Glene antébrachiale
Glene antébrachiale Slopinamasis svyravimas
Slopinamasis svyravimas Semi-modals
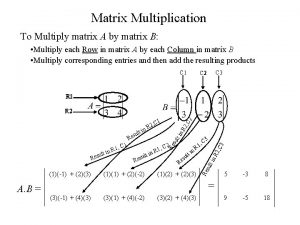
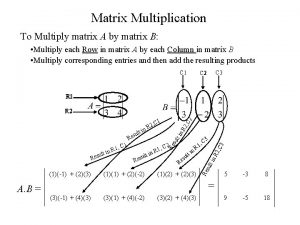
Semi-modals Matrix multiplication linear algebra
Matrix multiplication linear algebra Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ Bổ thể
Bổ thể Phản ứng thế ankan
Phản ứng thế ankan Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Chúa yêu trần thế alleluia
Chúa yêu trần thế alleluia điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Hệ hô hấp
Hệ hô hấp Số nguyên tố là
Số nguyên tố là Công của trọng lực
Công của trọng lực đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới ưu thế lai là gì
ưu thế lai là gì Các môn thể thao bắt đầu bằng tiếng chạy
Các môn thể thao bắt đầu bằng tiếng chạy Tư thế ngồi viết
Tư thế ngồi viết Bàn tay mà dây bẩn
Bàn tay mà dây bẩn Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Tư thế ngồi viết
Tư thế ngồi viết Chó sói
Chó sói Thẻ vin
Thẻ vin V cc cc
V cc cc Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Hươu thường đẻ mỗi lứa mấy con
Hươu thường đẻ mỗi lứa mấy con Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Frameset trong html5
Frameset trong html5 Phép trừ bù
Phép trừ bù Lời thề hippocrates
Lời thề hippocrates Glasgow thang điểm
Glasgow thang điểm đại từ thay thế
đại từ thay thế Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi