Dynamic Programming CISC 4080 Computer Algorithms CIS Fordham

Dynamic Programming CISC 4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang

Outline • Introduction via example: Fibonacci, rod cutting • Characteristics of problems that can be solved using dynamic programming • More examples: • Maximal subarray problem • Longest increasing subsequence problem • Two dimensional problem spaces • Longest common subsequence • Matrix chain multiplication 2

Dynamic Programming 3

Rod Cutting Problem • A company buys long steel rods (of length n), and cuts them into shorter one to sell • integral length only • cutting is free • rods of diff lengths sold for diff. price • Goal: cut rod into shorter ones to sell for maximal profit 4

Rod Cutting Problem • Input: • given rod’s length n • p[i]: selling price of rod of length i, for example: • Output: maximal achievable total settling price, Rn, over all possible ways to cut out n to shorter pieces and sell • For example, if n=4, we could cut it into: • • • {4}: do not cut ==> total selling price is $9 {3, 1} ==> selling price $8+$1=$9 {2, 2} ==> $10 multiset: {2, 1, 1} ==> $7 allow duplicate elements order does not matter {1, 1, 1, 1}==> $4 5

Solution Space • Evaluate all possible ways, and pick one with highest total selling price? • how many ways to write n as sum of positive integers? • n=4, there are 5 ways: 4=4, 4=1+3, 4=2+2, 4=1+1+1+1, 4=2+1+1 • n=5: … • # of ways to cut n: # of ways to express n as positive integer linear combination of 1, 2, … 10, • this leads to exponential running time 6

Thinking Recursively • //return maximum profit achievable with a rod of length n • Cut. Rod (n, p[1…k]) • What’s the smallest problem(s) that we can solve trivially? • if n=0, n=1 • How to reduce the problem to smaller problems? 7

Recursion! • • • Cut. Rod (n, p[1…k]) //return rn What’s the smallest problem(s) that we can solve trivially? • if n=0, n=1 How to reduce the problem to smaller problems? • consider the first rod to cut out and sell, c 1 • c 1 can be 1, 2, 3, … , min (n, k) • we sell it for p[c 1], and have a rod of length n-c 1 remaining ==> a smaller problems • Just try all different c 1 and solve subproblems recursively: 8

Optimal substructure • Optimal substructure: Optimal solution to a problem of size n incorporates optimal solutions to problems of smaller size (n-1, n-2, … ). 9

Optimal Substructure => recursive solution • //return max. profit one can make with a rod of length n • Cut. Rod (n, p[1…k]) //What’s the smallest problem(s) that we can solve trivially? if n=0 return 0 if n=1 return p[1] //general case: consider the first rod to cut out and sell, cur. Max=0 for c 1=1, 2, 3, … , min (n, k) cur. Profit = p[c 1]+Max. Prof (n-c 1) cur. Max = max (cur. Profit, cur. Max) // done evaluating all possibilities return cur. Max 10

Running time? • //return max. profit one can make with a rod of length n • Cut. Rod (n, p[1…k]) //What’s the smallest problem(s) that we can solve trivially? if n=0 return 0 // for n > k if n=1 return p[1] //general case: consider the first rod to cut out and sell, cur. Max=0 for c 1=1, 2, 3, … , min (n, k) cur. Profit = p[c 1]+Cut. Rod (n-c 1) cur. Max = max (cur. Profit, cur. Max) // done evaluating all possibilities return cur. Max 11

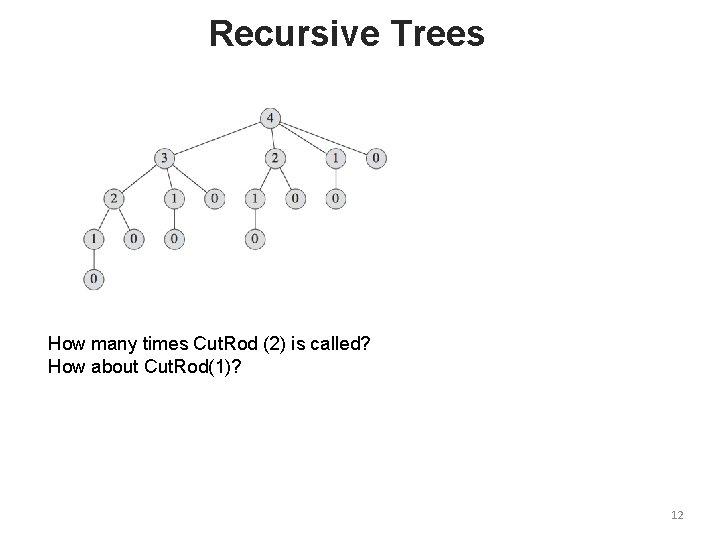
Recursive Trees How many times Cut. Rod (2) is called? How about Cut. Rod(1)? 12

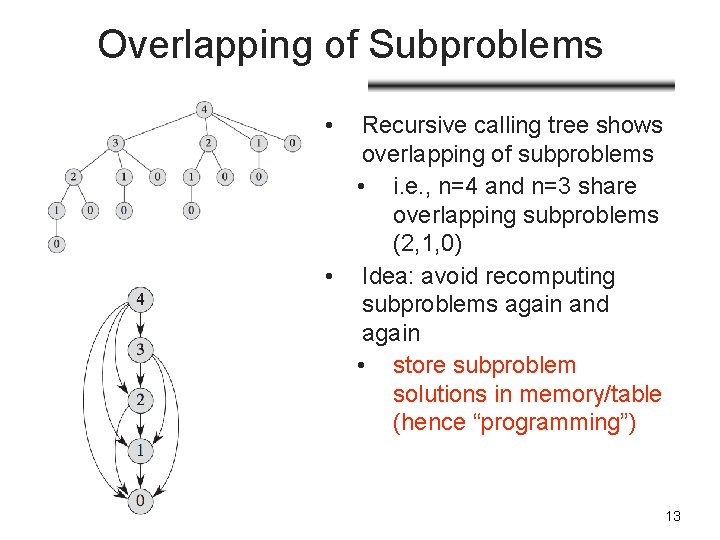
Overlapping of Subproblems • Recursive calling tree shows overlapping of subproblems • i. e. , n=4 and n=3 share overlapping subproblems (2, 1, 0) • Idea: avoid recomputing subproblems again and again • store subproblem solutions in memory/table (hence “programming”) 13

Dynamic Programming: two approach • memoization (recursive, top-down) • improve recursive solution by storing subproblem solution in a table • when need solution of a subproblem, check if it has been solved before, • if not, calculate it and store result in table • if yes, access result stored in table • a top-down approach: • start with the problem at hand (a larger problem), and solve subproblems as needed (recursively)

Memoization illustrated in code //return max. profit one can make with a rod of length n Cut. Rod (n, p[1…k]) 1. create an array r[1…n], filled with -1 (indicate “not calculated yet”) 2. Cut. Rod. Helper (n, p, r) Cut. Rod. Helper (n, p[1…k], r[]) 1. if r[n] >=0 return r[n] //if it has been calculated already 2. // no need to recalculate, return the stored result 3. 4. if n==0 return 0 //base case 5. //general case 6. cur. Max=0 7. for c 1=1, 2, 3, … , min (n, k) 8. cur. Profit = p[c 1] + Cut. Rod. Helper (n-c 1) 9. cur. Max = max(cur. Profit, cur. Max) 10. 11. r[n]= cur. Max //save result in r[] for future reference 12. return cur. Max 15

Dynamic Programming: Tabulation • Memoization (recursive, top-down) • Tabulation • Iteratively solve smaller problems first, move the way up to larger problems • bottom-up method: as we solve smaller problems first, and then larger and larger one • => when solving a problem, all subproblems solutions that are needed have already been calculated

Bottom-up • //return max. profit one can make with a rod of length n • Cut. Rod. Bottom. Up (n, p[1…k]) 1. create an array r[1…n] //store subproblem solutions 2. r[0] = 0 3. for i=1 to n // solve smaller problems first … 4. // calculate ri , max revenue for rod length i 5. cur. Max=0 6. for c 1=1, 2, 3, … , min (i, k) 7. cur. Profit = p[c 1]+ r[i-c 1] 8. cur. Max = max(cur. Profit, cur. Max) 9. r[i]= cur. Max //save result in r[] for future reference 10. 11. return r[n] 17

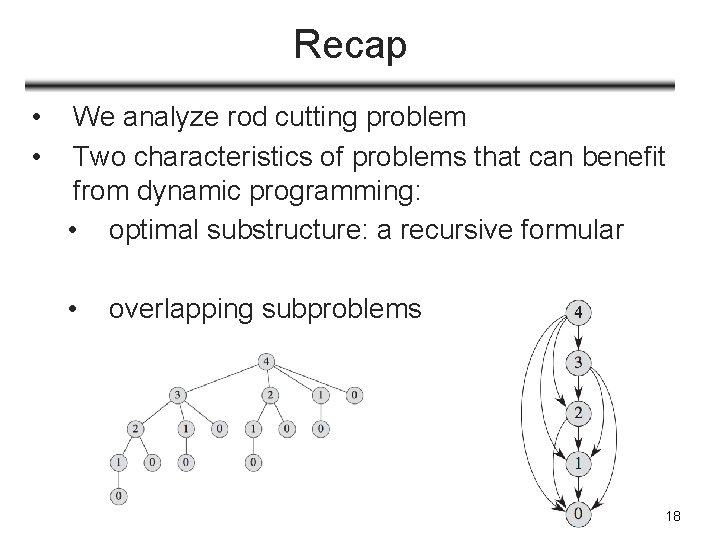
Recap • • We analyze rod cutting problem Two characteristics of problems that can benefit from dynamic programming: • optimal substructure: a recursive formular • overlapping subproblems 18

Recap (2) • How dynamic programming works: • Memoization: recursion with table • Tabulation: iteratively solve all possible subproblems, and work our way from small problems to large problems 19

Exercises • Copy given C++ program for rod cutting • copy. Rod. Cut • cd Cut. Rod; Compile and run • Exercise #1: • add some cout statement to find out how many times Max. Prof (3) is called when Max. Prof(6) is called from main. • Exercise #2: • So far, we focus on finding , max. revenue… • but what cutting achieves ? • How to extend the functions to output/return the cutting? • e. g. , n=4, cutting 2, 2, r_4=… 20

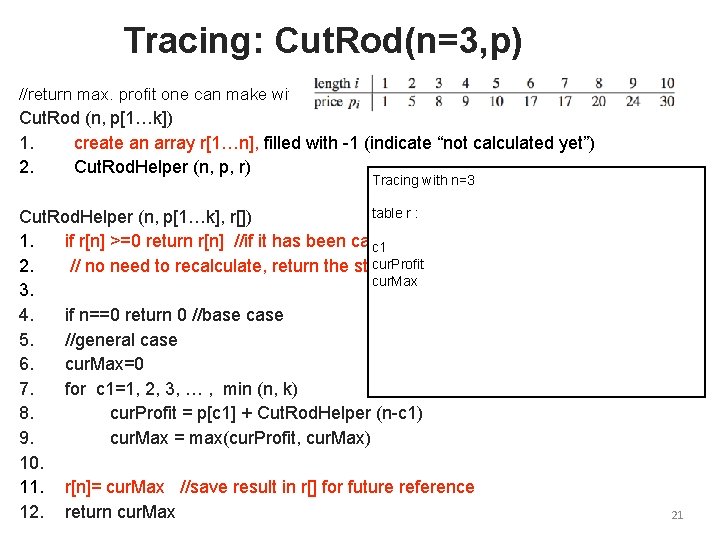
Tracing: Cut. Rod(n=3, p) //return max. profit one can make with a rod of length n Cut. Rod (n, p[1…k]) 1. create an array r[1…n], filled with -1 (indicate “not calculated yet”) 2. Cut. Rod. Helper (n, p, r) Tracing with n=3 table r : Cut. Rod. Helper (n, p[1…k], r[]) 1. if r[n] >=0 return r[n] //if it has been calculated already c 1 cur. Profit 2. // no need to recalculate, return the stored result cur. Max 3. 4. if n==0 return 0 //base case 5. //general case 6. cur. Max=0 7. for c 1=1, 2, 3, … , min (n, k) 8. cur. Profit = p[c 1] + Cut. Rod. Helper (n-c 1) 9. cur. Max = max(cur. Profit, cur. Max) 10. 11. r[n]= cur. Max //save result in r[] for future reference 12. return cur. Max 21

Tabulation: Tracing n=5 • //return max. profit one can make with a rod of length n • Cut. Rod. Bottom. Up (n, p[1…k]) 1. create an array r[1…n] //store subproblem solutions 2. r[0] = 0 3. for i=1 to n // solve smaller problems first … 4. // calculate ri , max revenue for rod length i 5. cur. Max=0 6. for c 1=1, 2, 3, … , min (i, k) 7. cur. Profit = p[c 1]+ r[i-c 1] 8. cur. Max = max(cur. Profit, cur. Max) 9. r[i]= cur. Max //save result in r[] for future reference 10. 11. return r[n] 22

Discussion: Knapsack • Input • given weight capacity of a knapsack, W • n different objects, with weights and values given by array w[ ], v[ ] • • i-th type of objects weighs w[i] and has a value of v[i] there are infinite quantities of each object type • Output: objects to put into knapsack so that total value is maximized and total weights <= W • For now, focus on max. total value • Discussion: • how is this similar to Rod Cutting? 23

Discussion: Knapsack • Input: weight capacity of a knapsack, W; n different objects, with weights and values given by array w[ ], v[ ] • i-th type of objects weighs w[i] and has a value of v[i] • there are infinite quantities of each object type • Output: objects to put into knapsack so that total value is maximized and total weights <= W • For example: W=13, w[4]={5, 3, 8, 4}, v[4]={10, 25, 8} in the figure • Let Vk be max total value possible when weight capacity is k • V 13 = ? Consider first object to put in knapsack: • if object #1 => total max. value would be 10 + max value possible with 13 -5 • if object #2 => total max. value would be …. • if object #i => total max. value would be What would be V 13? 24

Optimal substructure in Knapsack • Input: weight capacity of a knapsack, W; n different objects (of infinite quantities) with weights and values given by array w[ ], v[ ] • Output: objects so that total value is maximized and total weights <= W • For example: W=13, w[4]={5, 3, 8, 4}, v[4]={10, 25, 8} in the figure • Let Vk be max total value possible when weight capacity is k • Recursive formula for Vk • A illustration of calculation of W 13 • Run the following command to copy the sample code: copy. Rod. Cut 25

Knapsack: extension • Input: weight capacity of a knapsack, W; n different objects (of infinite quantities) with weights and values given by array w[ ], v[ ] • Output: objects so that total value is maximized and total weights <= W • Let Vk be max total value possible when weight capacity is k • What’s the set of objects (multi-set) that achieve Vk? • The i that achieves the max value above • and then the object i 1 chosen for k-w[i] • and then the object i 2 chosen for k-w[i]-w[i 1] • … until the weight capacity ==0 or < min(w) a table obj[]: obj[k] store the first object to chose when capacity is k (the one that maximize …) Output the multi-set achieving Vk, using obj[ ] array Demo… • • • 26

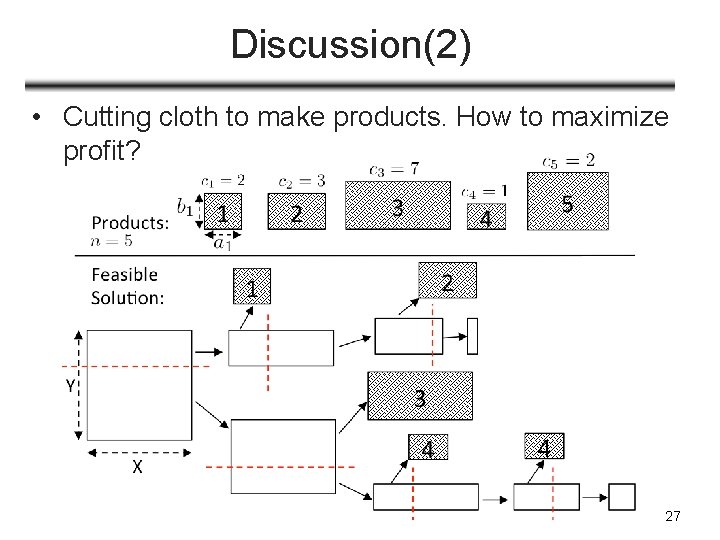
Discussion(2) • Cutting cloth to make products. How to maximize profit? 27

Outline • • Introduction via example: rod cutting Characteristics of problems that can be solved using dynamic programming • More examples: • Maximal subarray problem • Longest increasing subsequence problem • Two dimensional problem spaces • Longest common subsequence • Matrix chain multiplication • Summary 28

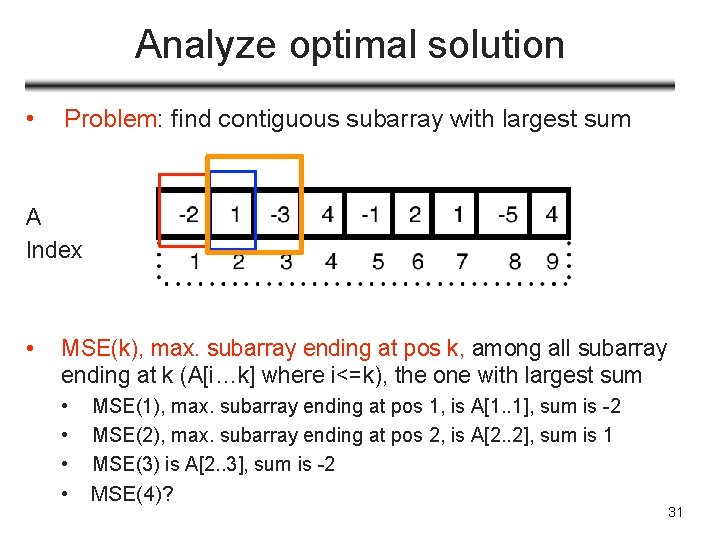
maximum (contiguous) subarray • • Problem: find contiguous subarray within an array (containing at least one number) which has largest sum • If given the array [-2, 1, -3, 4, -1, 2, 1, -5, 4], • contiguous subarray [4, -1, 2, 1] has largest sum = 6 Brute-force? • brute-force: n 2 or n 3 Divide-and-conquer: T(n)=2 T(n/2)+O(n), T(n)=nlogn Dynamic programming? 29

Analyze optimal solution • Problem: find contiguous subarray with largest sum • • Sample Input: [-2, 1, -3, 4, -1, 2, 1, -5, 4] (array of size n=9) How does solution to this problem relates to smaller subproblem? • If we divide up array into two halves • [-2, 1, -3, 4, -1, 2, 1, -5, 4] //find Max. Sub in this array • • [-2, 1, -3, 4, -1] [2, 1, -5, 4] • still need to consider subarray that spans both halves • This does not lead to a dynamic programming sol. Need a different way to define smaller subproblems! 30

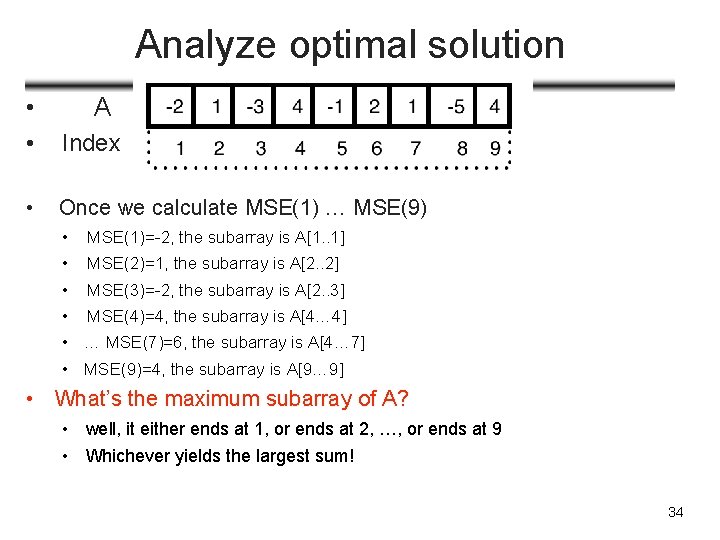
Analyze optimal solution • Problem: find contiguous subarray with largest sum A Index • MSE(k), max. subarray ending at pos k, among all subarray ending at k (A[i…k] where i<=k), the one with largest sum • • MSE(1), max. subarray ending at pos 1, is A[1. . 1], sum is -2 MSE(2), max. subarray ending at pos 2, is A[2. . 2], sum is 1 MSE(3) is A[2. . 3], sum is -2 MSE(4)? 31

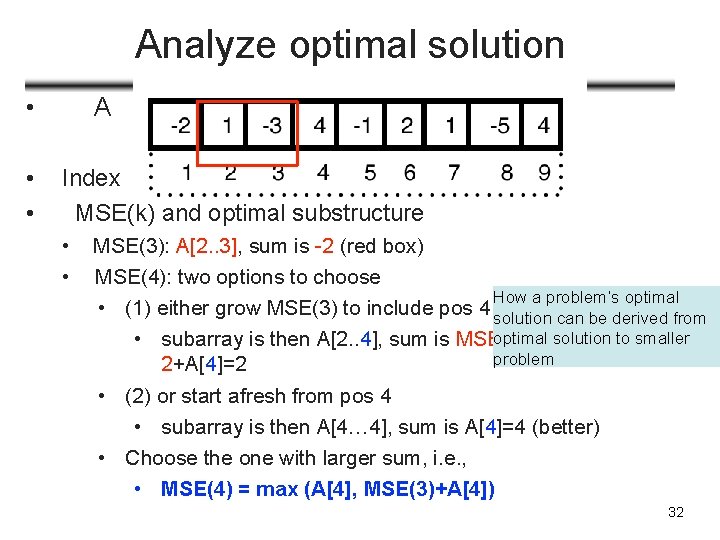
Analyze optimal solution • • • A Index MSE(k) and optimal substructure • • MSE(3): A[2. . 3], sum is -2 (red box) MSE(4): two options to choose How a problem’s optimal • (1) either grow MSE(3) to include pos 4 solution can be derived from optimal solution to smaller • subarray is then A[2. . 4], sum is MSE(3)+A[4]=problem 2+A[4]=2 • (2) or start afresh from pos 4 • subarray is then A[4… 4], sum is A[4]=4 (better) • Choose the one with larger sum, i. e. , • MSE(4) = max (A[4], MSE(3)+A[4]) 32

Analyze optimal solution • • A Index MSE(4)=4, array is A[4… 4] MSE(k) and optimal substructure • Max. subarray ending at k is the larger between A[k…k] and Max. subarray ending at k-1 extended to include A[k] MSE(k) = max (A[k], MSE(k-1)+A[k]) • MSE(5)= , subarray is • MSE(6) • MSE(7) • MSE(8) • MSE(9) 33

Analyze optimal solution • A • Index • Once we calculate MSE(1) … MSE(9) • MSE(1)=-2, the subarray is A[1. . 1] • MSE(2)=1, the subarray is A[2. . 2] • MSE(3)=-2, the subarray is A[2. . 3] • MSE(4)=4, the subarray is A[4… 4] • … MSE(7)=6, the subarray is A[4… 7] • MSE(9)=4, the subarray is A[9… 9] • What’s the maximum subarray of A? • well, it either ends at 1, or ends at 2, …, or ends at 9 • Whichever yields the largest sum! 34

Idea to Pseudocode • Idea 1) Calculate MSE(1) … MSE(n) MSE(1)= A[1] MSE(i) = max (A[i], A[i]+MSE(i-1)); 2) Return max of MSE(i), for i=1, 2, …n int Max. Sub. Array (int A[1…n], int & start, int & end) { // Use array MSE to store the MSE(i) MSE[1]=A[1]; max. Sub. Array = MSE[1]; //use tabulation/bottom up to calculate MSE for (int i=2; i<=n; i++) { MSE[i] = ? ? max. Sub. Array = max(max. Sub. Array, MSE[i]); } return max. Sub. Array; Practice: 1) fill in ? ? } 2) How to find out starting and ending index of the max. subarray? 35

Running time Analysis int Max. Sub. Array (int A[1…n], int & start, int & end) { // Use array MSE to store the MSE(i) MSE[1]=A[1]; max_MSE = MSE[1]; for (int i=2; i<=n; i++) { MSE[i] = ? ? if (MSE[i] > max_MSE) { max_MSE = MSE[i]; } } return max_MSE; • • • It’s easy to see that running time is O(n) • a loop that iterates for n-1 times Recall other solutions: • brute-force: n 2 or n 3 • Divide-and-conquer: nlogn Dynamic programming wins! } 36

What is DP? When to use? • We have seen several optimization problems • brute force solution • divide and conquer • dynamic programming • To what kinds of problem is DP applicable? • • Optimal substructure: Optimal solution to a problem of size n incorporates optimal solution to problem of smaller size (1, 2, 3, … n-1). Overlapping subproblems: small subproblem space and common subproblems 37

Optimal substructure • • Optimal substructure: Optimal solution to a problem of size n incorporates optimal solution to problem of smaller size (1, 2, 3, … n-1). Rod cutting: find rn (max. revenue for rod of len n) Sol to problem instance of size n-1, n-2, … 1 rn = max (p[1]+rn-1, p[2]+rn-2, p[3]+rn-3, …, p[n-1]+r 1, p[n]) • A recurrence relation (recursive formula) • => Dynamic Programming: Build an optimal solution to the problem from solutions to subproblems • We solve a range of sub-problems as needed 38

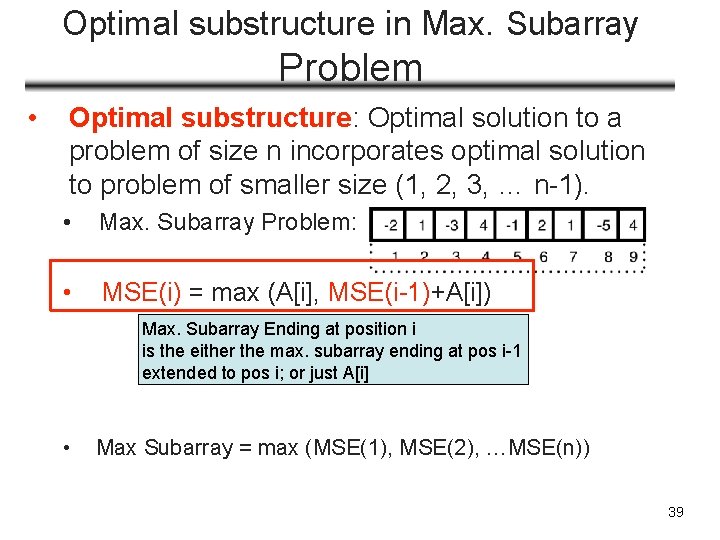
Optimal substructure in Max. Subarray Problem • Optimal substructure: Optimal solution to a problem of size n incorporates optimal solution to problem of smaller size (1, 2, 3, … n-1). • Max. Subarray Problem: • MSE(i) = max (A[i], MSE(i-1)+A[i]) Max. Subarray Ending at position i is the either the max. subarray ending at pos i-1 extended to pos i; or just A[i] • Max Subarray = max (MSE(1), MSE(2), …MSE(n)) 39

Overlapping Subproblems • space of subproblems must be “small” • • • DP algorithms take advantage of this property • • • total number of distinct subproblems is a polynomial in input size (n) a recursive algorithm revisits same problem repeatedly, i. e. , optimization problem has overlapping subproblems. solve each subproblem once, store solutions in a table Look up table for sol. to repeated subproblem using constant time per lookup. In contrast: divide-and-conquer solves new subproblems at each step of recursion. 40

Outline • • Introduction via example: rod cutting Characteristics of problems that can be solved using dynamic programming • More examples: • Maximal subarray problem • Longest increasing subsequence problem • Two dimensional problem spaces • Longest common subsequence • Matrix chain multiplication • Summary 41

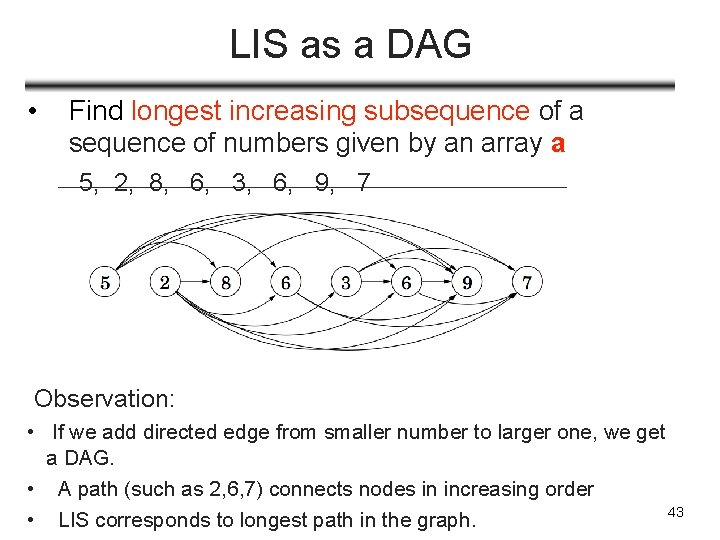
Longest Increasing Subsequence • • Input: a sequence of numbers given by an array a Output: a longest subsequence (a subset of the numbers taken in order) that is increasing (ascending order) • Example, given a sequence • 5, 2, 8, 6, 3, 6, 9, 7 • There are many increasing subsequence: 5, 8, 9; or 2, 9; or 8 • The longest increasing subsequence is: 2, 3, 6, 9 (length is 4) 42

LIS as a DAG • Find longest increasing subsequence of a sequence of numbers given by an array a 5, 2, 8, 6, 3, 6, 9, 7 Observation: • If we add directed edge from smaller number to larger one, we get a DAG. • A path (such as 2, 6, 7) connects nodes in increasing order 43 • LIS corresponds to longest path in the graph.

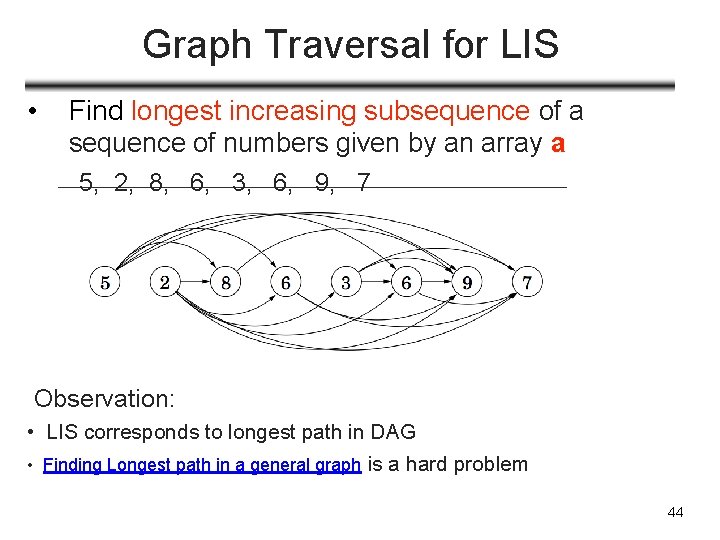
Graph Traversal for LIS • Find longest increasing subsequence of a sequence of numbers given by an array a 5, 2, 8, 6, 3, 6, 9, 7 Observation: • LIS corresponds to longest path in DAG • Finding Longest path in a general graph is a hard problem 44

Dynamic Programming Sol: LIS • Find Longest Increasing Subsequence of a sequence of numbers given by an array a 1 2 3 4 5 6 7 8 Let L(n) be the length of LIS ending at n-th number L(1) = 1, LIS ending at pos 1 is 5 L(2) = 1, LIS ending at pos 2 is 2 L(7)= // how to relate to L(1), …L(6)? • Consider LIS ending at a[7] (i. e. , 9). What’s the number before 9? . … ? , 9 45

Dynamic Programming Sol: LIS • Given a sequence of numbers given by an array a 1 2 3 4 5 6 7 8 Let L(n) be length of LIS ending at n-th number Consider all increasing subsequence ending at a[7] (i. e. , 9). • What’s the number before 9? • It can be either NULL, or 6, or 3, or 6, 8, 2, 5 (all those numbers pointing to 9) • If the number before 9 is 3 (a[5]), what’s max. length of this seq? L(5)+1 where the seq is …. 3, 9 LIS ending at pos 5 46

Dynamic Programming Sol: LIS • Given a sequence of numbers given by an array a Pos: 1 2 3 4 5 6 7 8 Let L(n) be length of LIS ending at n-th number Consider all increasing subsequence ending at a[7] (i. e. , 9). • It can be either NULL, or 6, or 3, or 6, 8, 2, 5 (all those numbers pointing to 9) • L(7)=max(1, L(6)+1, L(5)+1, L(4)+1, L(3)+1, L(2)+1, L(1)+1) • L(8)=? 47

Dynamic Programming Sol: LIS • Given a sequence of numbers given by an array a Pos: 1 2 3 4 5 6 7 8 Let L(n) be length of LIS ending at n-th number. Recurrence relation: Note that the i’s in RHS is always smaller than the j • How to implement? Running time? • LIS of sequence = Max (L(i), 1<=i<=n) // the longest among all 48

Outline • • Introduction via example: rod cutting Characteristics of problems that can be solved using dynamic programming • More examples (skipped) • Maximal subarray problem • Longest increasing subsequence problem • Two dimensional problem spaces • Add up to N problem • Knapsack with one of each • Longest common subsequence • Matrix chain multiplication • Summary 49

K-Sum Problem (add up to K) • Problem: Given an array of int values and integer K, find out whethere is a subset of these numbers that add up to K (and output one such subset) • cannot use a number multiple times • bool Add. Up. To. K (int numbers[], int n, int K) • K=100, n=9, numbers: 22 34 18 30 76 1 3 1 2 3 4 5 6 19 80 7 8 9 • In lab 2: 1) use binary number to enumerate all 2 n subsets, 2) use recursive function to check all possible subsets (include numbers[i] or not) • Now: use dynamic programming to improve recursive solution 50

K-Sum Problem (add up to K) • Problem: find out whethere is a subset of these numbers that add up to K (and output one such subset) • bool Add. Up. To. K (int numbers[], int num_len, int K) • K=100, num_len=9 numbers: 1 • Think recursively! • base case: 2 3 4 5 6 7 8 9 22 34 18 30 76 1 3 19 80 • general case: how to reduce it to smaller problem(s)? • hint: recall how we did it in Knapsack and Rod. Cut? 51

K-Sum Problem (add up to K) • Problem: find out whethere is a subset of these numbers that add up to K (and output one such subset) • bool Add. Up. To. K (int numbers[], int num_len, int K) • K=100, num_len=9 numbers: 1 2 3 4 5 6 7 8 9 22 34 18 80 76 1 3 19 20 • base cases • if K==0 return true • if K>0 and num_len==0 return false • general case: //how reduce to smaller problem? • • consider making one decision: include last number, 20, or not? if included it, then see if we can add up to 100 -20 using the rest of the numbers • if not, see if we can add up to 100 using the rest of the numbers. • two subproblems (underlined above) 52

K-Sum Problem (add up to K) Problem: find out whethere is a subset of these numbers that add up to K (and output one such subset) bool Add. Up. To. K (int numbers[], int num_len, int K) 1 2 3 4 5 6 7 8 9 { //base cases 22 34 18 80 76 1 3 19 20 if K==0 return true if K>0 and num_len==0 return false // general case: consider include last number, 20 (in this case), or not? if (Add. Up. To. K (numbers, num_len-1, K-numbers[num_len-1])) return true; //we can make K by including last num… else if (Add. Up. To. K (numbers, num_len-1, K)) return true; //we can make K by not including last num else return false; //not possible } 53

K-Sum Problem (add up to K) • Problem: find out whethere is a subset of these numbers that add up to K (and output one such subset) • bool Add. Up. To. K (int numbers[], int num_len, int K) • K=100, num_len=9 numbers: 1 2 3 4 5 6 7 8 9 22 34 18 80 76 1 3 19 20 • Overlapping subproblems? • can you give an example of overlapping subproblems? • sol: • if we include 20, but not 19, 3, 1, 76 => Add. Up. To. K(… 4, 80) //use numbers[1… 4] to make 80 • if we include 19, 1 and not 20, 3, 76 => Add. Up. To. K(…, 4, 80): same subproblems 54

K-Sum Problem (add up to K) • Problem: find out whethere is a subset of these numbers that add up to K (and output one such subset) • bool Add. Up. To. K (int numbers[], int num_len, int K) • K=100, num_len=9 numbers: 1 2 3 4 5 6 7 8 9 22 34 18 80 76 1 3 19 20 • Overlapping subproblems? • can you give an example of overlapping subproblems? • sol: • if we include 20, but not 19, 3, 1, 76 => Add. Up. To. K(… 4, 80) //use numbers[1… 4] to make 80 • if we include 19, 1 and not 20, 3, 76 => Add. Up. To. K(…, 4, 80): same subproblems • Memoization or Tabulation: store subproblem solutions 55

K-Sum Problem: tabulation /*whethere is a subset of these numbers that add up to K, and output one such subset */ bool Add. Up. To. K_Tabulation (int numbers[], int num_len, int K) { bool C[K+1][num_len+1]; // C[k][n]: can we add up to k using numbers[1…n] 1 2 3 4 5 6 7 8 9 for n=0 to num_len C[0][n] = 0 // if K==0 return true 22 34 18 80 76 1 3 19 20 for k=1 to K C[k][0] = false //fill in array row by row, left to right for k=1 to K for n=1 to num_len if C[k][n-1]==true C[k][n]=true //we can make k without last number //otherwise, can we include numbers[n] to make k? else if k==numbers[n] C[k][n] = true; else if k>numbers[n] and C[k-numbers[n]][n-1]==true C[k][n] = true; else //k<numbers[n] or cannot make k-numbers[n] using numbers[1…n-1] C[k][n] = false return C[K][num_len]; 56

Knapsack without repetition • Input: given weight capacity of a knapsack, W; and n different objects, with weights and values given by array w[ ], v[ ] • • there is one of each type object: one gold bar, one diamond… finding a subset of objects … • Output: objects to select so that total value is maximized and total weights <= W • We could enumerate all possible subsets (as in lab 2) • => Running time • Plan: • recursive solution • use memoization or tabulation to improve 57

/* Output max. value, and objects to select @param W: given weight capacity, >=0 @ param n: # of objects, n>=0 @param w, v: weights and values @return max value achievable from obj [1…n] */ Just Recursion! • Problem size has two dimensions: W and n Knapsack_Norepeat (W, w, v, n) • Recursive calls reduce problem size in one or both dimension { • eventually reach base case if W==0 or n == 0 //base case • Running time return 0 • in worst case T(n)=2 T(n-1) , n is the number of objects //general case: reduce to smaller problems? • ==> T(n) = 2 n //Q: include n-th obj or not, which one yields larger value? if (w[n] > W) //it’s possible to include n-th obj V 1 = Knapsack_Norepeat (W-w[n], w, v, n-1) + V[n] //if we include n-th obj V 2 = Knapsack_Norepeat (W, w, v, n-1) //if we don’t include n-th obj return max(V 1, V 2) else //impossible to include n-th obj // only one option: do not include n-th obj return Knapsack_Norepeat (W, w, v, n-1) } 58

Knapsack_Norepeat (W, w, v, n) { initialize V[W+1][n+1] to store solutions to subproblems // V[w][n] is the max value achievable with weight capacity w and obj 1…n fill V with -1 Knapsack_Norepeat_helper (W, w, v, n, V); } Recursion and Memoization Knapsack_Norepeat_helper (W, w, v, n, V) { if (V[w][n]>=0) // If the problem has been solved before…. return V[w][n] if (w==0 or n==0) V[w][n]= 0 return V[w][n] Running time analysis? T(w, n) = O (nm) //general case: reduce to smaller problems? //Q: include n-th obj or not, which one yields larger value? if (w[n] > W) //it’s possible to include n-th obj V 1 = Knapsack_Norepeat_helper (W-w[n], w, v, n-1, V) + V[n] V 2 = Knapsack_Norepeat_helper (W, w, v, n-1 , V) V[w][n] = max (V 1, V 2) return V[w][n] else //impossible to include n-th obj // only one option: do not include n-th obj V[w][n] = Knapsack_Norepeat_helper (W, w, v, n-1 , V) return V[w][n]; } 59

Outline • • • Introduction via example: rod cutting Characteristics of problems that can be solved using dynamic programming More one dimensional examples • • • Knapsack with repetition, Maximal subarray problem, Longest increasing subsequence use one dimensional array to store subproblem solutions Two dimensional problem spaces • K-Sum • Knapsack without repetition • Longest common subsequence • Matrix chain multiplication (skipped) 60

Longest Common Subseq. • Given a sequence, X = 〈x 1, x 2, …, xm〉, where xi is a letter from a certain alphabet, a subsequence of X is a subset of elements in sequence X taken in order but not necessarily consecutive e. g. , X = 〈A, B, C, B, D, A, B〉, here are some subsequences of X: 〈A, B, D〉, 〈B, C, D, B〉, 〈A〉, áñ, áA, B, C, B, D, A, Bñ • How many possible subsequences are there for X? • • e. g. , DNA alphabet is {A, C, G, T} • Denote length of a sequence X by |X|, which is the number of letters in the sequence • e. g. , X = 〈A, B, C, B, D, A, B〉, |X|=7

Longest Common Subseq. • Given two sequences, X = 〈x 1, x 2, …, xm〉, Y = 〈y 1, y 2, …, yn〉 where xi, yi are letters, find a longest common subsequence (LCS) of X and Y • a sequence that is subsequence of X, and is a subsequence of Y • and is of the same or longer length than all common subsequences of X and Y

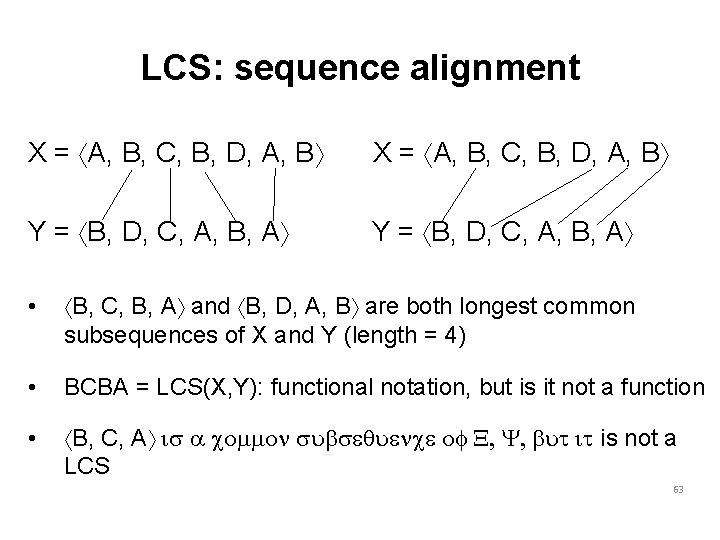
LCS: sequence alignment X = áA, B, C, B, D, A, Bñ Y = áB, D, C, A, B, Añ • áB, C, B, Añ and áB, D, A, Bñ are both longest common subsequences of X and Y (length = 4) • BCBA = LCS(X, Y): functional notation, but is it not a function • áB, C, Añ is a common subsequence of X, Y, but it is not a LCS 63

Brute-Force Solution 1. /* Check every subsequence of X[1. . m] to see if it is also a subsequence of Y[1. . n]. */ 2. LCS (X, Y) 3. { 4. for each of 2 m subsequence, s, of X 5. //check if s is a subsequence of Y, O(n) time 6. k = |s| //k is length of s 7. j=1 8. for i=1 to k 9. while ( Y[j]!=s[i] and j<=n) 10. j++ // scan Y for a letter matching s[i] 11. if j>n // cannot match s[i] 12. break and s not a subsequence Y 13. 14. s is subsequence of Y, update longest 15. 16. } Worst-case running time: O(n 2 m) 64

Thinking about subproblems • Given a sequence X = 〈x 1, x 2, …, xm〉, we define i-th prefix of X (for i = 0, 1, 2, …, m) as Xi = 〈x 1, x 2, …, xi〉 • for example, X = 〈A, B, C, B, D, A, B〉, we have the following prefixes: • X 2 = 〈A, B〉, X 4 = 〈A, B, C, B〉, • X 0 = 〈〉, a special prefix that is an empty sequence • X 7 = 〈A, B, C, B, D, A, B〉, a special prefix that is original sequence • What’s X 5 ? • We focus on length of LCS first, • Define: c[i, j] = | LCS (Xi, Yj) = |LCS(X[1. . i], Y[1. . j])|, i. e. , the length of a LCS of i-th prefix of X, Xi = áx 1, x 2, …, xiñ, and j-th prefix of Y, Yj = áy 1, y 2, …, yjñ. 65

Recursive Solution. Case 1 /* Return the longest subsequence of X, Y @param X: is a string @param Y: is a string @return the longest common subsequence of X and Y*/ LCS (X, Y) m = |X|, n = |Y| if X[m] ==Y[n] e. g. : X = áA, B, D, Eñ Y = áZ, B, Eñ • find a LCS of Xm-1 and Yn-1, (here, X 3 = áA, B, Dñ and Y 2 = áZ, Bñ, <B>) • append X[m] to the LCS of Xm-1 and Yn-1 => <B, E> 66

Recursive Solution. Case 2 if X[m] ¹ Y[n] e. g. : X = áA, B, D, Gñ Y = áZ, B, Dñ Either the G or the D is not in the LCS (they cannot be both in LCS) LCS(X, Y) = Longer { LCS(Xm - 1, Y), If we ignore last element in X LCS (X, Yn-1)} If we ignore last element in Y • Must solve two subproblems 67

/* Return the longest subsequence of X, Y Recursion @param X: is a string @param Y: is a string Three Questions? @return the longest common subsequence of X and Y*/ LCS (X, Y) { m=|X|, n=|Y| if (|X| == 0 or |Y|==0) return “ “; //empty string //general case X = áA, B, D, Eñ // can we match last letters of X and Y? Y = áZ, B, Eñ if X[m] == Y[n] return LCS(Xm-1, Yn-1)+X[m] //concatenated with last letter else // Xm and Yn cannot be both in LCS X = áA, B, D, Gñ s 1 = LCS(Xm-1, Yn) Y = áZ, B, Dñ s 2 = LCS(Xm, Yn-1) return longer of s 1 and s 2 } Here we need to calculate prefix (Xm-1, Yn-1), and pass them to recursive calls 68

/* Return the longest subsequence of X, Y @param X : is a string Recursion @param Y: is a string Three Questions? @return the longest common subsequence of Xm and Yn*/ LCS (X, Y, m, n ) { if (m== 0 or n==0) return “ “; //empty string //general case // can we match last letters of X and Y? if X[m] == Y[n] X = áA, B, D, Eñ return LCS(X, Y, m-1, n-1)+X[m] //concatenated with last letter Y = áZ, B, Eñ else // Xm and Yn cannot be both in LCS s 1 = LCS(X, Y, m-1, n ) s 2 = LCS(X, Y, m, n-1) X = áA, B, D, Gñ return longer of s 1 and s 2 Y = áZ, B, Dñ } // keep X, Y as they are, use parameters to specify prefix length // subproblem’s size is given by m and n, at least one dimension is decreased 69

Optimal substructure & Overlapping Subproblems • A recursive solution contains a “small” number of distinct subproblems repeated many times. • • • e. g. , LCS (5, 5) depends on LCS(4, 4), LCS(4, 5), LCS(5, 4) Exercise: Draw subproblem dependence graph • each node is a subproblem • directed edge represents “calling”, “uses solution of” relation Small number of distinct subproblems: • total number of distinct LCS subproblems for two strings of lengths m and n is mn. 70

Tabulation to avoid recalculation • Given two sequences X = áx 1, x 2, …, xmñ, Y = áy 1, y 2, …, ynñ • To ease tracing, we focus on finding length of LCS c[i, j] = | LCS (Xi, Yj) | // length of LCS c[i-1, j-1] + 1 if X[i]= Y[j] c[i, j] = max(c[i, j-1], c[i-1, j]) otherwise (i. e. , if X[i] ≠ Y[j]) 71

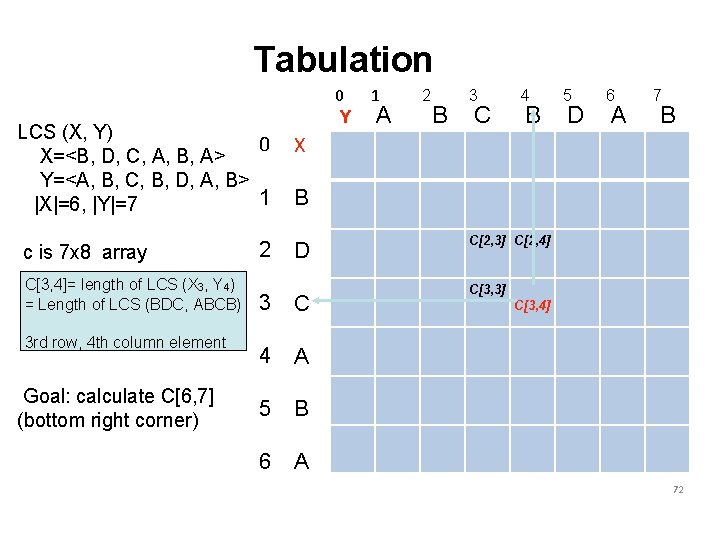
Tabulation 0 Y LCS (X, Y) 0 X=<B, D, C, A, B, A> Y=<A, B, C, B, D, A, B> 1 |X|=6, |Y|=7 X 2 D c is 7 x 8 array C[3, 4]= length of LCS (X 3, Y 4) = Length of LCS (BDC, ABCB) 3 rd row, 4 th column element Goal: calculate C[6, 7] (bottom right corner) 1 A 2 B 3 C 4 B 5 D 6 A 7 B B 3 C 4 A 5 B 6 A C[2, 3] C[2, 4] C[3, 3] C[3, 4] 72

Memoization algorithm Memoization: After computing a solution to a subproblem, store it in a table. Subsequent calls check the table to avoid redoing work. LCS (X, Y) create and initialize table c[m][n] to -1 LCS_helper(X, Y, |X|, |Y|, c) LCS_helper(X, Y, i, j, c) if c[i, j] = NIL // LCS(i, j) has not been solved yet then if i==0 or j==0 c[i, j]=0 return 0 if x[i] = y[j] c[i, j] ←LCS_helper(x, y, i– 1, j– 1, c) + 1 else c[i, j] ←max{ LCS_helper(x, y, i– 1, j, c), LCS_helper(x, y, i, j– 1, c) } else return c[i, j] 73

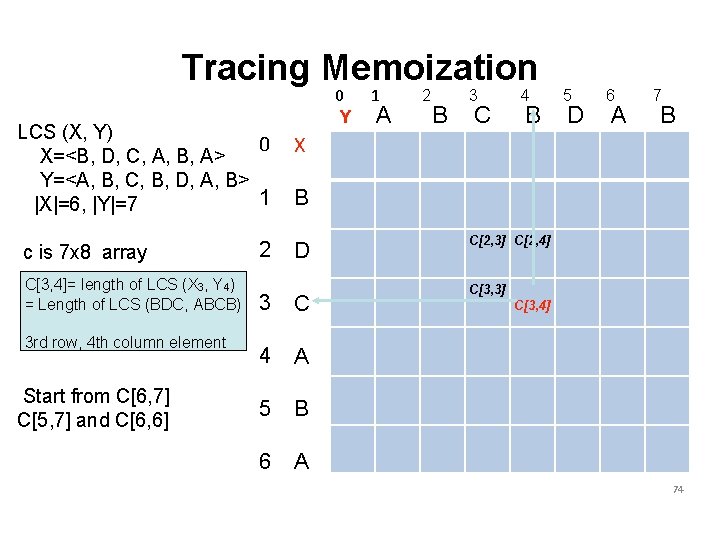
Tracing Memoization 0 Y LCS (X, Y) 0 X=<B, D, C, A, B, A> Y=<A, B, C, B, D, A, B> 1 |X|=6, |Y|=7 X 2 D c is 7 x 8 array C[3, 4]= length of LCS (X 3, Y 4) = Length of LCS (BDC, ABCB) 3 rd row, 4 th column element Start from C[6, 7] C[5, 7] and C[6, 6] 1 A 2 B 3 C 4 B 5 D 6 A 7 B B 3 C 4 A 5 B 6 A C[2, 3] C[2, 4] C[3, 3] C[3, 4] 74

Bottom-Up 0 Y Initialization: base c[i, j] = 0 if i=0, or j=0 0 X //Fill table row by row // from left to right for (int i=1; i<=m; i++) for (int j=1; j<=n; j++) update c[i, j] 1 B 2 D 3 C return c[m, n] 4 A 5 B 6 A Running time = Θ(mn) C[3, 4]= length of LCS (X 3, Y 4) = Length of LCS (BDC, ABCB) 3 rd row, 4 -th column element 1 A 2 B 3 C 4 B 5 D 6 A 7 B C[2, 3] C[2, 4] C[3, 3] C[3, 4] 75

Dynamic-Programming Algorithm Reconstruct LCS tracing backward: Where do we get value of C[i, j] from? • C[i-1, j-1]+1 ( ) • C[i-1, j] ( ) • C[i, j-1] ( ) Use a table b[i][j] to store above arrows (Up, Left, LU) A B C B D A B 0 0 0 0 0 1 1 1 D 0 0 1 1 1 2 2 2 C 0 0 1 2 2 2 A 0 1 1 2 2 2 3 3 B 0 1 2 2 3 3 3 4 0 1 2 2 3 3 4 4 B A Output B C B Output A 76

Remark • Longest common subsequence algorithm is similar to • minimum edit distance problem (used by spell checker to suggest a correction) • Needleman-Wansh Alg. (used in bioinformatics to align protein or nucleotide sequences) 77

Matrix: a 2 D (rectangular) array of numbers, symbols, or expressions, arranged in rows and columns. e. g. , a 2 × 3 matrix (there are two rows and three columns) Each element of a matrix is denoted by a variable with two subscripts, a 2, 1 element at second row and first column of a matrix A. an m × n matrix A: 78

Matrix Multiplication: Dimension of A, B, and A x B? Total (scalar) multiplication: 4 x 2 x 3=24 Total (scalar) multiplication: n 2 xn 1 xn 3 79

Multiplying a chain of Matrix Multiplication Given a sequence/chain of matrices, e. g. , A , A there are different ways to calculate A A A 1 1 2 2 3, 3 1. (A 1 A 2)A 3) 2. (A 1(A 2 A 3)) Dimension of A 1: 10 x 100 A 2: 100 x 5 A 3: 5 x 50 all yield the same result But not same efficiency 80

Matrix Chain Multiplication Given a chain <A 1, A 2, … An> of matrices, where matrix Ai has dimension pi-1 x pi, find optimal fully parenthesize product A 1 A 2…An that minimizes number of scalar multiplications. Chain of matrices <A , A , A >: five distinct ways 1 A 1: p 1 x p 2 2 A 2: p 2 x p 3 3 4 A 3: p 3 x p 4 A 4: p 4 x p 5 # of multiplication: p 3 p 4 p 5+ p 2 p 3 p 5+ p 1 p 2 p 5 Find the one with minimal multiplications? 81

Matrix Chain Multiplication • Given a chain <A 1, A 2, … An> of matrices, where matrix Ai has dimension pi-1 x pi, find optimal fully parenthesize product A 1 A 2…An that minimizes number of scalar multiplications. • Let m[i, j] be the minimal # of scalar multiplications needed to calculate Ai. Ai+1…Aj (m[1…n]) is what we want to calculate) • Recurrence relation: how does m[i…j] relate to smaller problem • First decision: pick k (can be i, i+1, …j-1) where to divide Ai. Ai+1…Aj into two groups: (Ai…Ak)(Ak+1…Aj) • (Ai…Ak) dimension is pi-1 x pk, (Ak+1…Aj) dimension is pk x pj 82

Summary • Keys to DP • • Recursive algorithm => optimal Substructure overlapping subproblems Write recurrence relation for subproblem: i. e. , how to calculate solution to a problem using sol. to smaller subproblems Implementation: • memoization (table+recursion) • bottom-up table based (smaller problems first) • Insights and understanding comes from practice! 83