Minimum Spanning Trees CISC 4080 Computer Algorithms CIS

Minimum Spanning Trees CISC 4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang

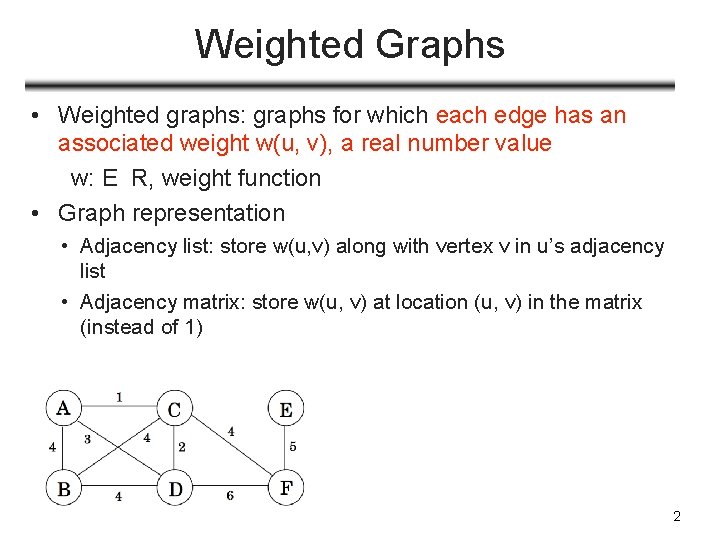
Weighted Graphs • Weighted graphs: graphs for which each edge has an associated weight w(u, v), a real number value w: E R, weight function • Graph representation • Adjacency list: store w(u, v) along with vertex v in u’s adjacency list • Adjacency matrix: store w(u, v) at location (u, v) in the matrix (instead of 1) 2

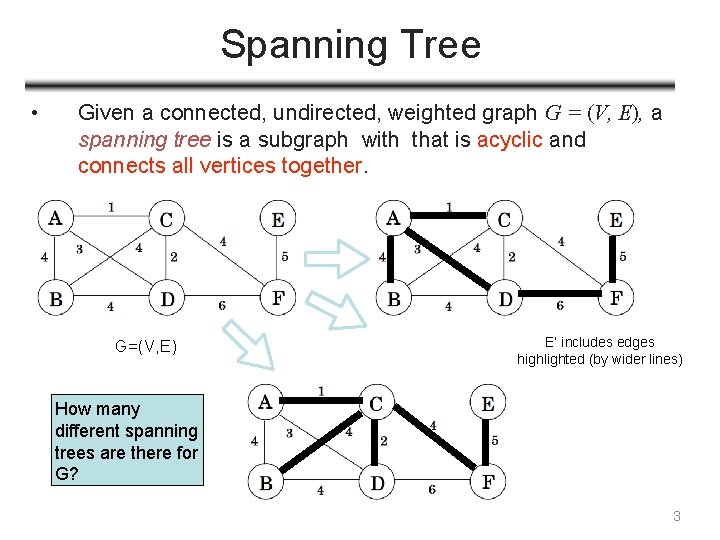
Spanning Tree • Given a connected, undirected, weighted graph G = (V, E), a spanning tree is a subgraph with that is acyclic and connects all vertices together. G=(V, E) E’ includes edges highlighted (by wider lines) How many different spanning trees are there for G? 3

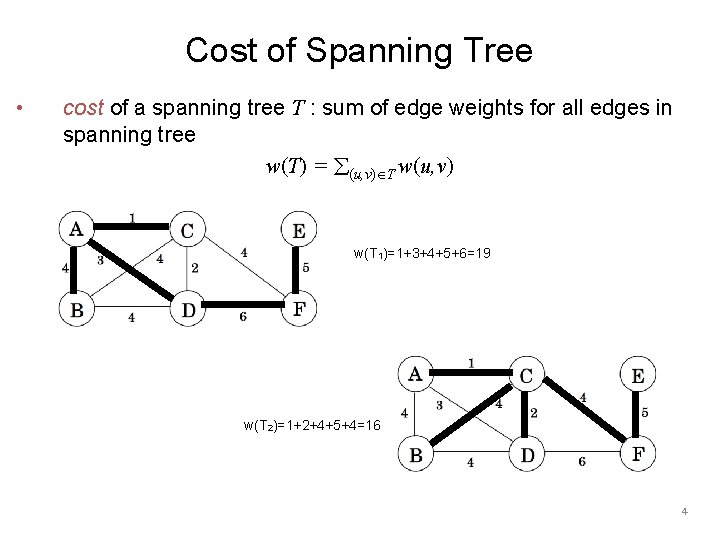
Cost of Spanning Tree • cost of a spanning tree T : sum of edge weights for all edges in spanning tree w(T) = å(u, v)ÎT w(u, v) w(T 1)=1+3+4+5+6=19 w(T 2)=1+2+4+5+4=16 4

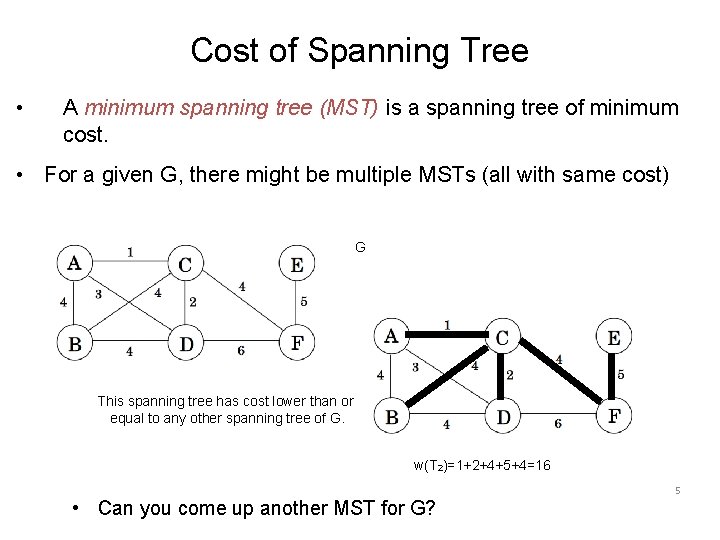
Cost of Spanning Tree • A minimum spanning tree (MST) is a spanning tree of minimum cost. • For a given G, there might be multiple MSTs (all with same cost) G This spanning tree has cost lower than or equal to any other spanning tree of G. w(T 2)=1+2+4+5+4=16 5 • Can you come up another MST for G?

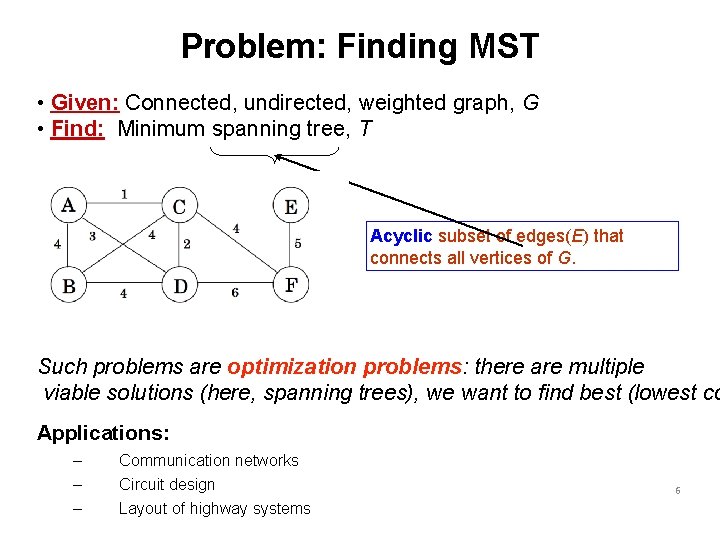
Problem: Finding MST • Given: Connected, undirected, weighted graph, G • Find: Minimum spanning tree, T Acyclic subset of edges(E) that connects all vertices of G. Such problems are optimization problems: there are multiple viable solutions (here, spanning trees), we want to find best (lowest co Applications: – – – Communication networks Circuit design Layout of highway systems 6

Greedy Algorithms • A problem solving strategy • other strategies: brute force, divide and conquer, randomization, dynamic programming, … • Greedy algorithms/strategies for solving optimization problem • build up a solution step by step • (local optimization) in each step always choose the option that offers best immediate benefits (a myopic approach) • not worrying about global optimization… • Performance of greedy algorithms: • Sometimes yield optimal solution, sometimes yield suboptimal (i. e. , not optimal) • Sometimes: we can bound difference from optimal… 7

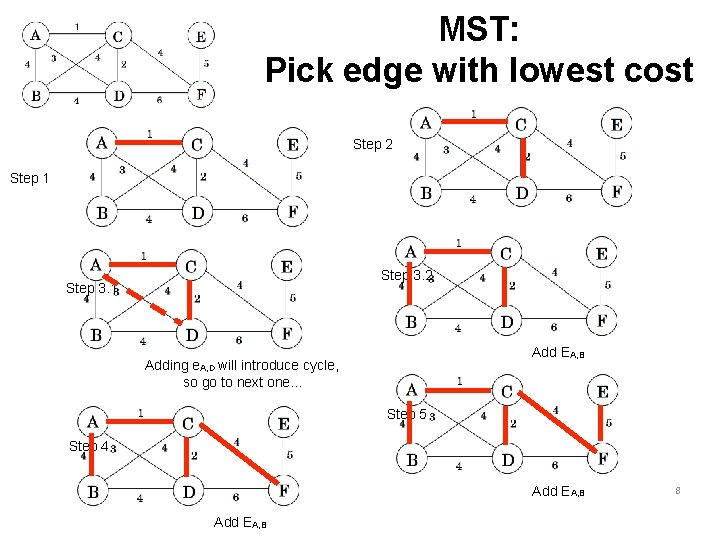
MST: Pick edge with lowest cost Step 2 Step 1 Step 3. 2 Step 3. 1 Add EA, B Adding e. A, D will introduce cycle, so go to next one… Step 5 Step 4 Add EA, B 8

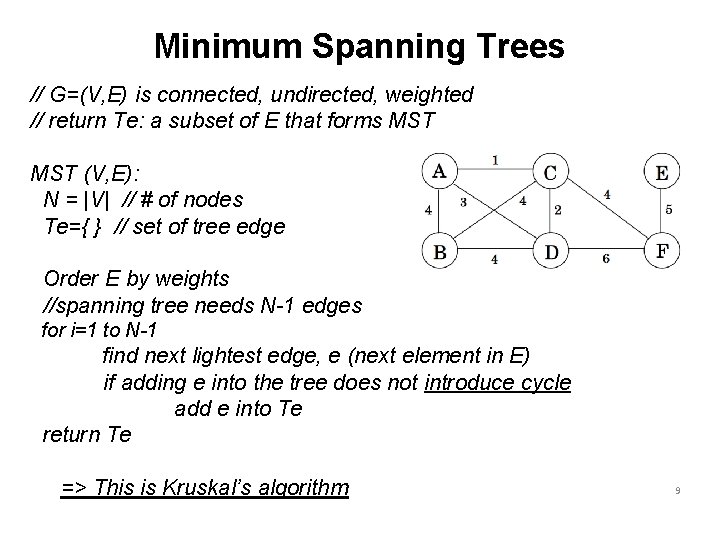
Minimum Spanning Trees // G=(V, E) is connected, undirected, weighted // return Te: a subset of E that forms MST (V, E): N = |V| // # of nodes Te={ } // set of tree edge Order E by weights //spanning tree needs N-1 edges for i=1 to N-1 find next lightest edge, e (next element in E) if adding e into the tree does not introduce cycle add e into Te return Te => This is Kruskal’s algorithm 9

Kruskal’s Algorithm Implementation detail: * Maintain sets of nodes that are connected by tree edges * find(u): return the set that u belongs to * find(u)=find(v) means u, v belongs to same group (i. e. , u and v are already connected)

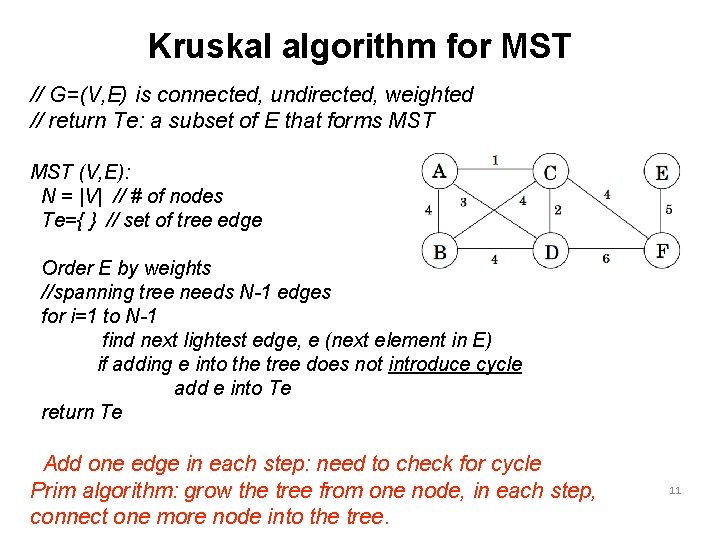
Kruskal algorithm for MST // G=(V, E) is connected, undirected, weighted // return Te: a subset of E that forms MST (V, E): N = |V| // # of nodes Te={ } // set of tree edge Order E by weights //spanning tree needs N-1 edges for i=1 to N-1 find next lightest edge, e (next element in E) if adding e into the tree does not introduce cycle add e into Te return Te Add one edge in each step: need to check for cycle Prim algorithm: grow the tree from one node, in each step, connect one more node into the tree. 11

Prim algorithm for MST // G=(V, E) is connected, undirected, weighted // return Et: set of tree edges in MST_Prim (V, E): 1. N = |V| // # of nodes 2. Q = empty priority queue of nodes 3. 4. //start from a random node s 5. s a node from V 6. cost[s] = 0; Q. enqueue (s) 7. Vt = {s} 8. 9. //initialize all other nodes 10. for each none u in V-Vt, 11. cost[u] = w(u, s) if (u, s) E 12. = if (u, s) 13. prev[u] = s if (u, s) 14. Q. enqueue (u) 15. 16. 17. Repeat for N times 18. //add lowest cost node to tree 19. u = Q. dequeue() 20. add u to Vt 21. add edge (prev[u], u) into Et 22. 23. //update all other nodes cost 24. for each node v in V-Vt 25. if w(u, v) < cost[v] 26. cost[v] = w(u, v) 27. prev[v] = u 28. end of Repeat loop 29. 30. return Et 12

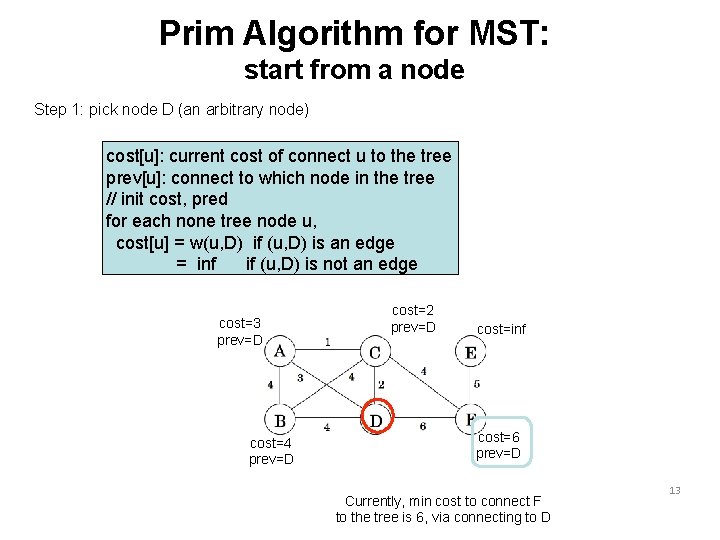
Prim Algorithm for MST: start from a node Step 1: pick node D (an arbitrary node) cost[u]: current cost of connect u to the tree prev[u]: connect to which node in the tree // init cost, pred for each none tree node u, cost[u] = w(u, D) if (u, D) is an edge = inf if (u, D) is not an edge cost=3 prev=D cost=4 prev=D cost=2 prev=D cost=inf cost=6 prev=D Currently, min cost to connect F to the tree is 6, via connecting to D 13

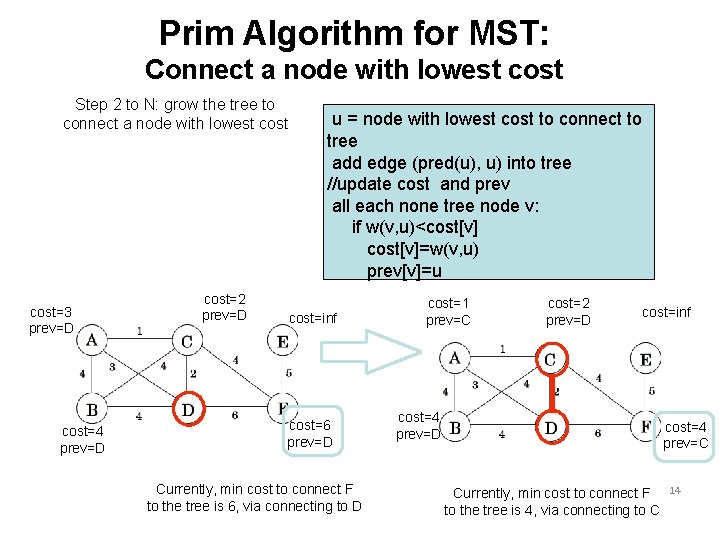
Prim Algorithm for MST: Connect a node with lowest cost Step 2 to N: grow the tree to connect a node with lowest cost=3 prev=D cost=4 prev=D cost=2 prev=D u = node with lowest cost to connect to tree add edge (pred(u), u) into tree //update cost and prev all each none tree node v: if w(v, u)<cost[v]=w(v, u) prev[v]=u cost=inf cost=6 prev=D Currently, min cost to connect F to the tree is 6, via connecting to D cost=1 prev=C cost=2 prev=D cost=inf cost=4 prev=D cost=4 prev=C Currently, min cost to connect F to the tree is 4, via connecting to C 14

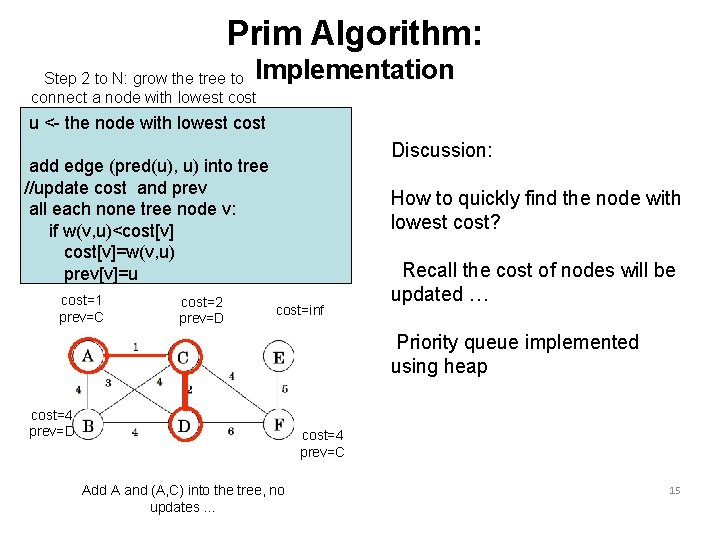
Prim Algorithm: Implementation Step 2 to N: grow the tree to connect a node with lowest cost u <- the node with lowest cost Discussion: add edge (pred(u), u) into tree //update cost and prev all each none tree node v: if w(v, u)<cost[v]=w(v, u) prev[v]=u cost=1 prev=C cost=2 prev=D How to quickly find the node with lowest cost? cost=inf Recall the cost of nodes will be updated … Priority queue implemented using heap cost=4 prev=D cost=4 prev=C Add A and (A, C) into the tree, no updates … 15

Summary • Minimal Spanning Tree Problem • application: finding the lowest cost way to connect a set of nodes • • an example of optimization problem Greedy algorithm • myopic, choose what’s looks to be the best option at current step. • • sometimes lead to optimal solution, sometimes not Two MST algorithms • Kruscal: grow the tree by adding one edge a time (choose the edge with lowest weight and does not introduce cycle) • Prim: grow the tree by adding one node a time, choosing the 16