Lecture 8 Paradigm 6 Dynamic Programming n Popularized

Lecture 8. Paradigm #6 Dynamic Programming n Popularized by Richard Bellman ("Dynamic Programming", Princeton University Press, 1957; call number QA 264. B 36). Chapter 15 of CLRS. n Typically, dynamic programming reduces the complexity of a problem from 2 n to O(n 3) or O(n 2) or even O(n). n It does so by keeping track of already computed results in a bottom-up fashion, hence avoiding enumerating all possibilities. n Typically applies to optimization problems.

Example 1. Efficient multiplication of matrices (Section 15. 2 of CLRS. ) n Suppose we are given the following 3 matrices: M 1 10 x 100 n M 2 100 x 5 n M 3 5 x 50 n There are two ways to compute M 1*M 2*M 3: M 1 (M 2 M 3) or (M 1 M 2 ) M 3 n Since the cost of multiplying a p x q matrix by a q x r matrix is pqr multiplications, the cost of M 1 (M 2 M 3) is 100 x 50 + 10 x 100 x 50 = 75, 000 multiplications, while the cost of (M 1 M 2) M 3 is 10 x 100 x 5 + 10 x 50 = 7, 500 multiplications: a difference of n a factor of 10.

Naïve approach n We could enumerate all possibilities, and then take the minimum. How many possibilities are there? n The LAST multiplication performed is either M 1*(M 2. . . Mn), or (M 1 M 2)*(M 3. . . Mn), or. . . (M 1 M 2. . . )(Mn). Therefore, W(n), the number of ways to compute M 1 M 2. . . Mn, satisfies the following recurrence: W(n) = Σ 1 ≤ k < n W(k)W(n-k) --- Catalan number n Now it can be proved by induction that W(n) = (2 n-2 choose n 1)/n. Using Stirling's approximation, which says that n! = √(2πn) nn e-n (1 + o(1)), we have (2 n choose n) ~ 22 n/√(π n), n We conclude that W(n) ~ 4 n n-3/2, which means our naive approach will simply take too long (about 1010 steps when n = 20).

Dynamic Programming approach n Let’s avoid all the re-computation of the recursive approach. n Observe: Suppose the optimal method to compute M 1 M 2. . . Mn were to first compute M 1 M 2. . . Mk (in some order), then compute Mk+1. . . Mn (in some order), and then multiply these together. Then the method used for M 1 M 2. . . Mk must be optimal, for otherwise we could substitute a superior method and improve the optimal method. Similarly, the method used to compute Mk+1. . . Mn must also be optimal. The only thing left to do is to find the best possible k, and there are only n choices for that. n Letting m[i, j] represent the optimal cost for computing the product Mi. . . Mj, we see that m[i, j] = min { m[i, k] + m[k+1, j] + p[i-1]p[k]p[j] }, i ≤ k < j n k represents the optimal place to break the product Mi. . . Mj into two pieces. Here p is an array such that M 1 is of dimension p[0] × p[1], M 2 is of dimension p[1] × p[2], . . . etc.

Implementing it --- O(n 3) time n Like the Fibonacci number example, we cannot implement this by recursion. It will be exponential time. n MATRIX-MULT-ORDER(p) /* p[0. . n] is an array holding the dimensions of the matrices; matrix i has dimension p[i-1] x p[i] */ for i : = 1 to n do m[i, i] : = 0 for d : = 1 to n-1 do // d is the size of the sub-problem. for i : = 1 to n-d do j : = i+d m[i, j] : = infinity; for k : = i to j-1 do q : = m[i, k] + m[k+1, j] + p[i-1]*p[k]*p[j] if q < m[i, j] then m[i, j] : = q s[i, j] : = k // optimal position for breaking m[i, j] return(m, s)

Actually multiply the matrices n We have stored the break points k’s in the array s. s[i, j] represents the optimal place to break the product Mi. . . Mj. We can use s now to multiply the matrices: n MATRIX-MULT(M, s, i, j) /* Given the matrix s calculated by MATRIX-MULT-ORDER. The list of matrices M = [M 1, M 2, . . . , Mn]. Starting and finishing indices i and j. This routine computes the product Mi. . . Mj using the optimal method */ if j > i then X : = MATRIX-MULT(M, s, i, s[i, j]); Y : = MATRIX-MULT(M, s, s[i, j]+1, j); return(X*Y); else return(Mi)

Longest Common Subsequence (LCS) Application: comparison of two DNA strings Ex: X= {A B C B D A B }, Y= {B D C A B A} Longest Common Subsequence: X= AB C BDAB Y= BDCAB A Brute force algorithm would compare each subsequence of X with the symbols in Y

LCS Algorithm n if |X| = m, |Y| = n, then there are 2 m subsequences of x; we must compare each with Y (n comparisons) n So the running time of the brute-force algorithm is O(n 2 m) n Notice that the LCS problem has optimal substructure: solutions of subproblems are parts of the final solution – often, this is when you can use dynamic programming. n Subproblems: “find LCS of pairs of prefixes of X and Y”

LCS Algorithm n First we’ll find the length of LCS. Later we’ll modify the algorithm to find LCS itself. n Let Xi, Yj be the prefixes of X and Y of length i and j respectively n Let c[i, j] be the length of LCS of Xi and Yj n Then the length of LCS of X and Y will be c[m, n]

LCS recursive solution n We start with i = j = 0 (empty substrings of x and y) n Since X 0 and Y 0 are empty strings, their LCS is always empty (i. e. c[0, 0] = 0) n LCS of empty string and any other string is empty, so for every i and j: c[0, j] = c[i, 0] = 0

LCS recursive solution n When we calculate c[i, j], we consider two cases: n First case: x[i]=y[j]: one more symbol in strings X and Y matches, so the length of LCS Xi and Yj equals to the length of LCS of smaller strings Xi-1 and Yi-1 , plus 1

LCS recursive solution n Second case: x[i] != y[j] n As symbols don’t match, our solution is not improved, and the length of LCS(Xi , Yj) is the same as before, we take the maximum of LCS(Xi, Yj-1) and LCS(Xi-1, Yj) Think: Why can’t we just take the length of LCS(Xi-1, Yj-1)12? 9/26/2020

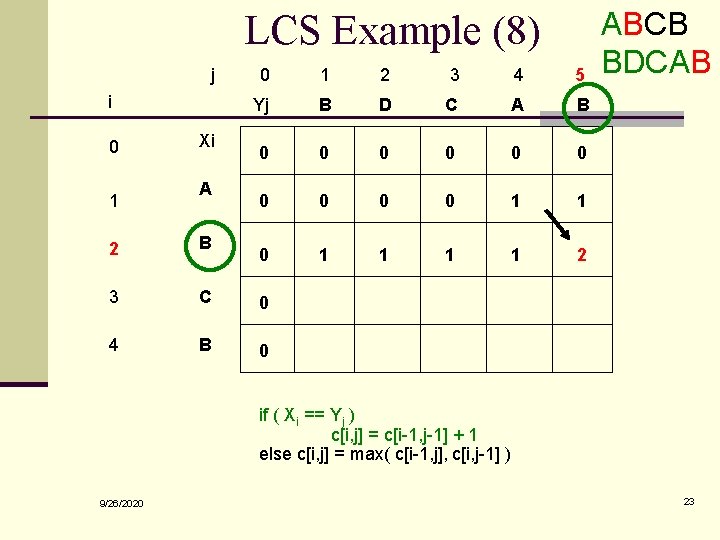
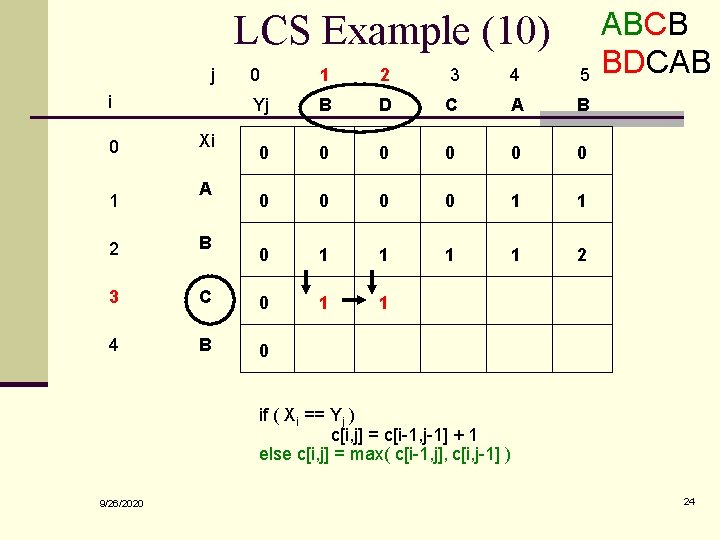
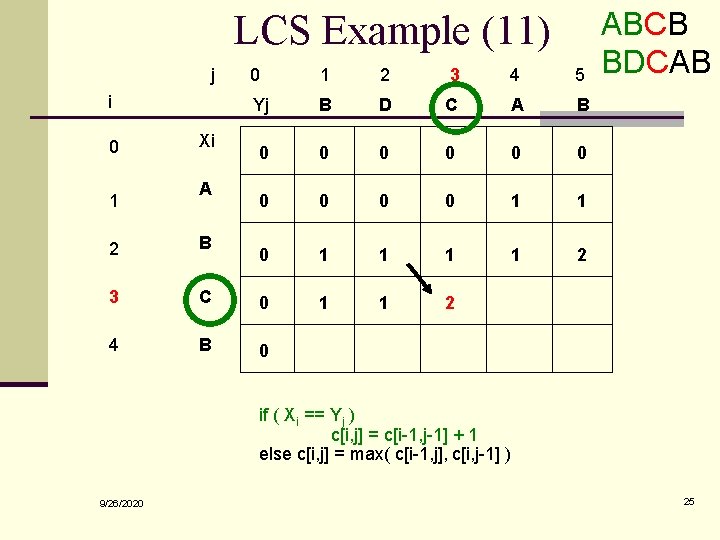
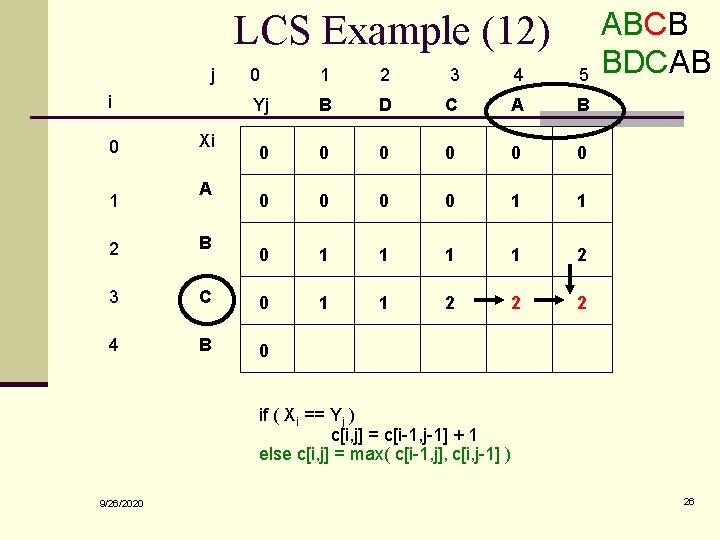
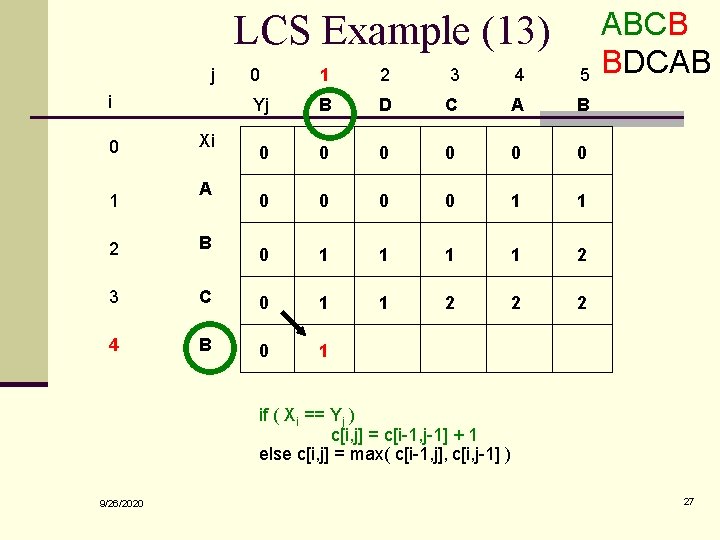
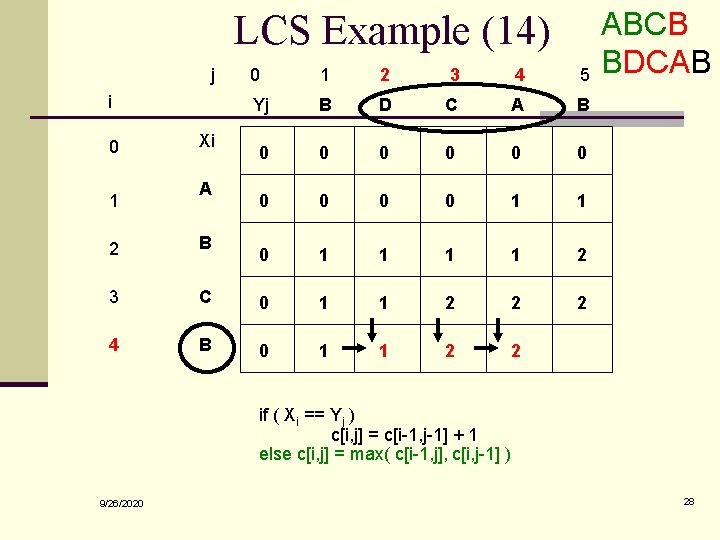
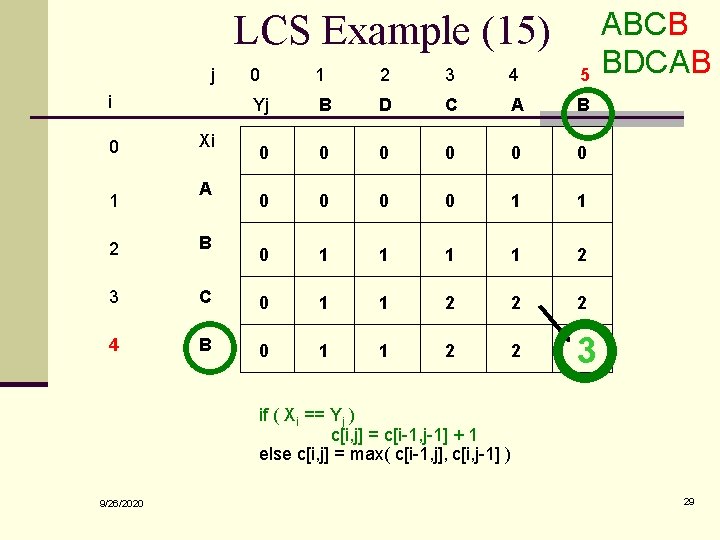
LCS Length Algorithm LCS-Length(X, Y) 1. m = length(X) // get the # of symbols in X 2. n = length(Y) // get the # of symbols in Y 3. for i = 1 to m c[i, 0] = 0 // special case: Y 0 4. for j = 1 to n c[0, j] = 0 // special case: X 0 5. for i = 1 to m // for all Xi 6. for j = 1 to n // for all Yj 7. if ( Xi == Yj ) 8. c[i, j] = c[i-1, j-1] + 1 9. else c[i, j] = max( c[i-1, j], c[i, j-1] ) 10. return c

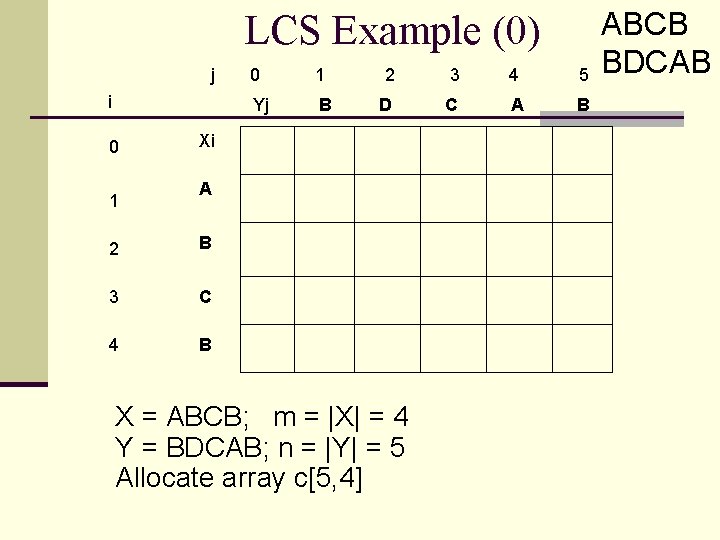
LCS Example We’ll see how LCS algorithm works on the following example: n X = ABCB n Y = BDCAB LCS(X, Y) = BCB X=AB C B Y= BD CAB

LCS Example (0) j i 0 1 Yj B 2 3 4 5 D C A B Xi A 2 B 3 C 4 B X = ABCB; m = |X| = 4 Y = BDCAB; n = |Y| = 5 Allocate array c[5, 4] ABCB BDCAB

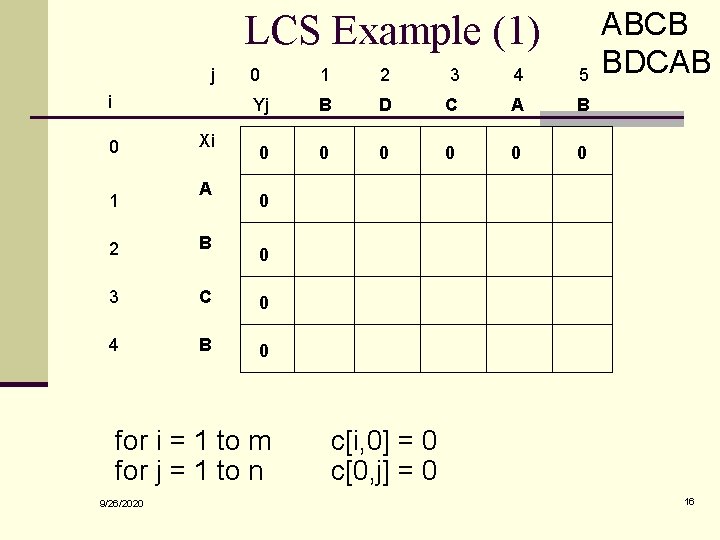
LCS Example (1) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 2 B 3 C 0 4 B 0 0 for i = 1 to m for j = 1 to n 9/26/2020 ABCB BDCAB c[i, 0] = 0 c[0, j] = 0 16

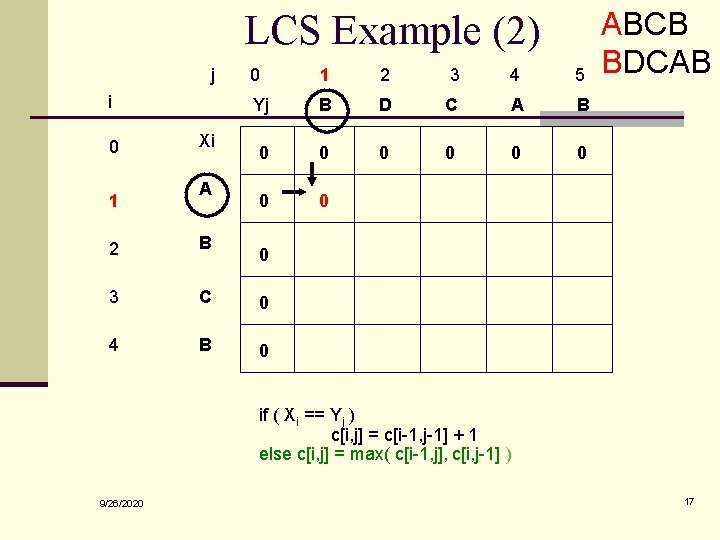
LCS Example (2) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 2 B 3 C 0 4 B 0 ABCB BDCAB 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 17

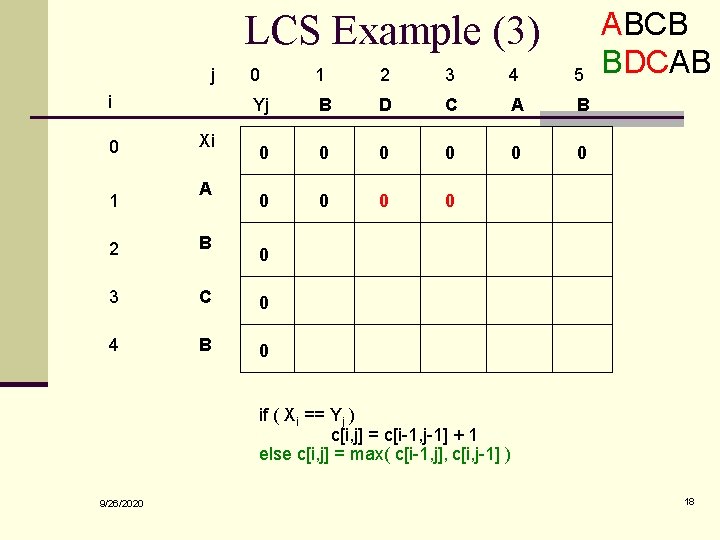
LCS Example (3) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 2 B 3 C 0 4 B 0 ABCB BDCAB 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 18

LCS Example (4) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 2 B 3 C 0 4 B 0 ABCB BDCAB 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 19

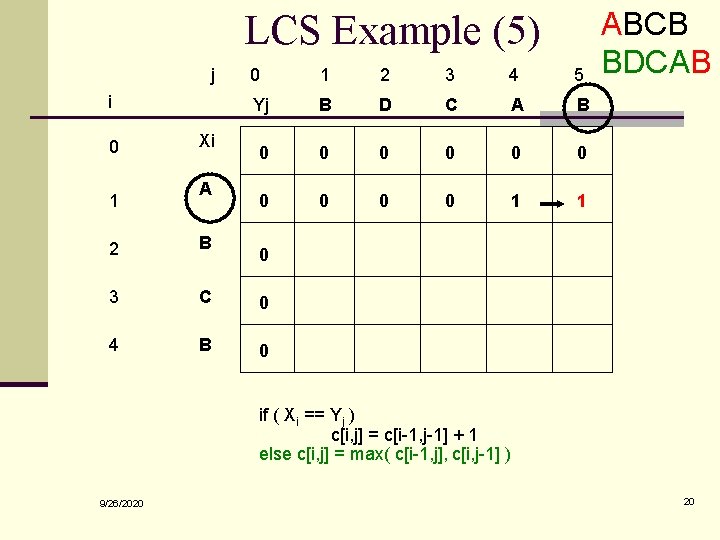
LCS Example (5) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 B 3 C 0 4 B 0 ABCB BDCAB 0 if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 20

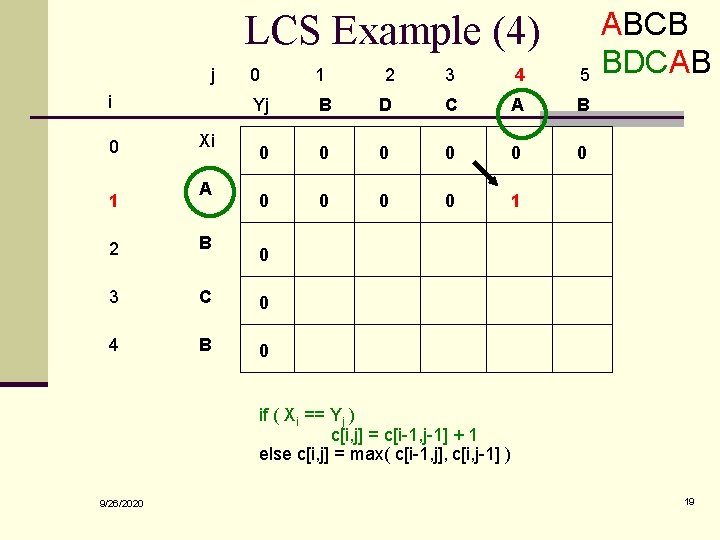
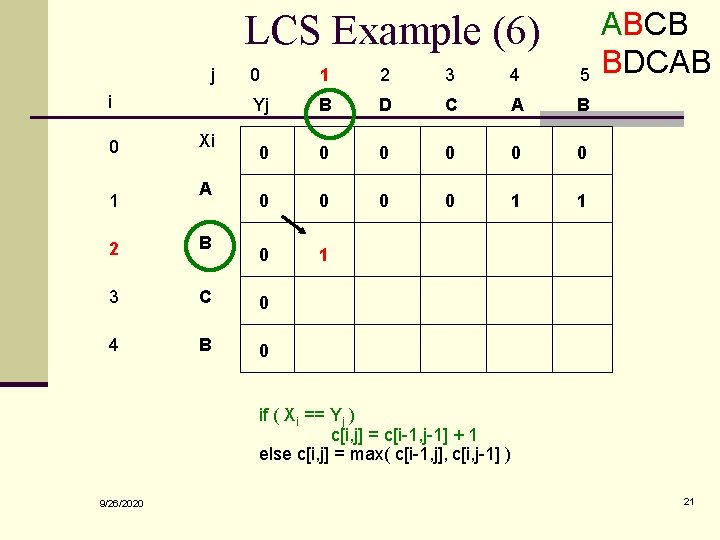
LCS Example (6) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 0 1 2 B 3 C 0 4 B 0 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 21

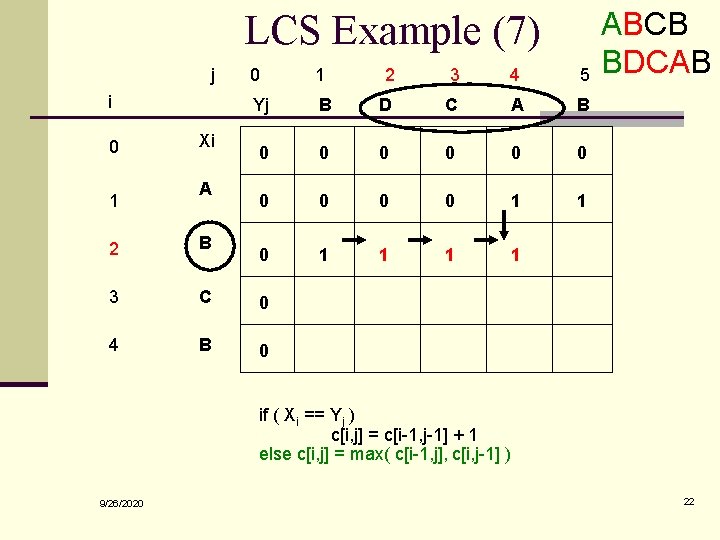
LCS Example (7) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 B 3 C 0 4 B 0 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 22

LCS Example (8) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 4 B 0 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 23

LCS Example (10) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 1 2 B 3 C 0 4 B 0 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 24

LCS Example (11) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 1 2 2 B 3 C 0 4 B 0 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 25

LCS Example (12) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 1 2 2 B 3 C 0 4 B 0 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 26

LCS Example (13) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 1 2 2 B 3 C 0 1 4 B 0 1 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 27

LCS Example (14) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 2 B 3 C 0 1 1 2 2 4 B 0 1 1 2 2 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 28

LCS Example (15) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 1 1 2 2 2 4 B 0 1 1 2 2 3 ABCB BDCAB if ( Xi == Yj ) c[i, j] = c[i-1, j-1] + 1 else c[i, j] = max( c[i-1, j], c[i, j-1] ) 9/26/2020 29

LCS Algorithm Running Time n LCS algorithm calculates the values of each entry of the array c[m, n] n So what is the running time? O(m*n) since each c[i, j] is calculated in constant time, and there are m*n elements in the array 9/26/2020 30

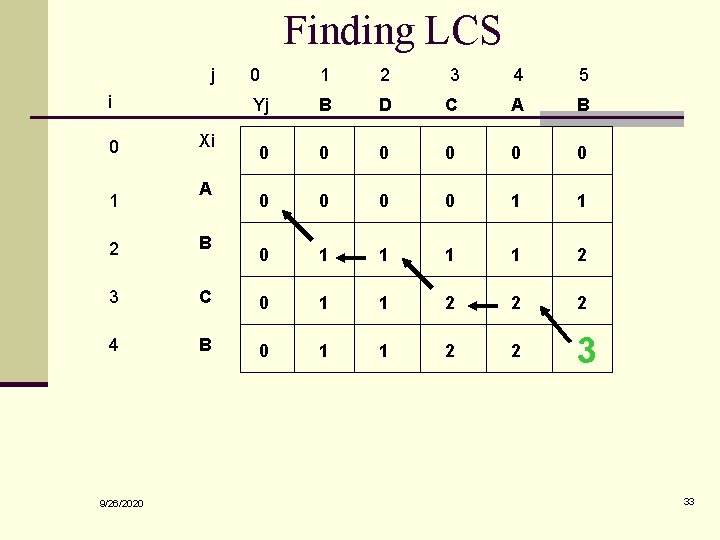
How to find actual LCS n So far, we have just found the length of LCS, but not LCS itself. n We want to modify this algorithm to make it output Longest Common Subsequence of X and Y Each c[i, j] depends on c[i-1, j] and c[i, j-1] or c[i-1, j-1] For each c[i, j] we can say how it was acquired: 2 2 2 3 9/26/2020 For example, here c[i, j] = c[i-1, j-1] +1 = 2+1=3 31

How to find actual LCS - continued n Remember that n n n So we can start from c[m, n] and go backwards Whenever c[i, j] = c[i-1, j-1]+1, remember x[i] (because x[i] is a part of LCS) When i=0 or j=0 (i. e. we reached the beginning), output remembered letters in reverse order 9/26/2020 32

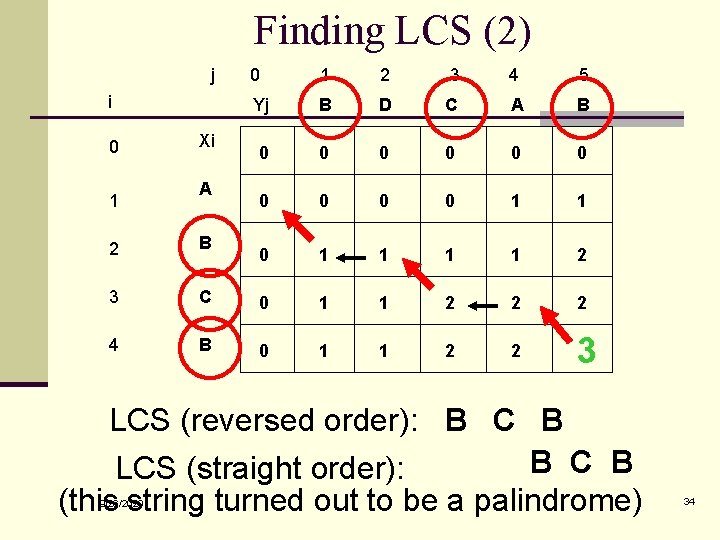
Finding LCS j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 1 1 2 2 2 4 B 0 1 1 2 2 3 9/26/2020 33

Finding LCS (2) j i 0 1 Xi A 0 1 2 3 4 5 Yj B D C A B 0 0 0 0 0 1 1 2 2 B 3 C 0 1 1 2 2 2 4 B 0 1 1 2 2 3 LCS (reversed order): B C B LCS (straight order): (this string turned out to be a palindrome) 9/26/2020 34

If we have time, we will do some exercises in class: n Edit distance: Given two text strings A of length n and B of length m, you want to transform A into B with a minimum number of operations of the following types: delete a character from A, insert a character into A, or change some character in A into a new character. The minimal number of such operations required to transform A into B is called the edit distance between A and B. n Balanced Partition: Given a set of n integers each in the range 0. . . K. Partition these integers into two subsets such that you minimize |S 1 - S 2|, where S 1 and S 2 denote the sums of the elements in each of the two subsets.