Advanced Dynamic Programming HKOI Training 2009 Hackson Leung

Advanced Dynamic Programming HKOI Training 2009 Hackson Leung 28 th March 2009 Acknowledgement: References and slides are extracted from: 1. Dynamic Programming, 19 -05 -2007, by Kelly Choi 2. [Advanced] Dynamic Programming, 24 -04 -2004, by cx

What should you know? Concept in Recurrence Basic Recursion [Intermediate] 2009 -01 -24 Functions [Advanced] 2009 -02 -21 Divide and Conquer [Intermediate] 2009 -03 -14 Refer to those notes if you are not familiar with

Simple Problem Revisited You have ∞ valued coins They are $0. 5, $1, $2 and $5 respectively Tell me how many ways I can make the total amount of N dollar(s) E. g. N = 1, we have $0. 5+$0. 5 $1 alone Condition I: Count $1+$2 and $2+$1 are different

Simple Problem Revisited How can we perform it in EXHAUSTION? Algorithm Count(Amount v) Begin if (v is zero) return 1; //Base Case Let sum = 0 for i in {0. 5, 1, 2, 5} if v – i >= 0 then sum = sum + Count(v-i) return sum End Count Performance: O(4 v)

Simple Problem Revisited How can we perform it in EXHAUSTION? Performance: O(4 v) When v is reasonably large (say, v = 18), the algorithm is very slow Cure?

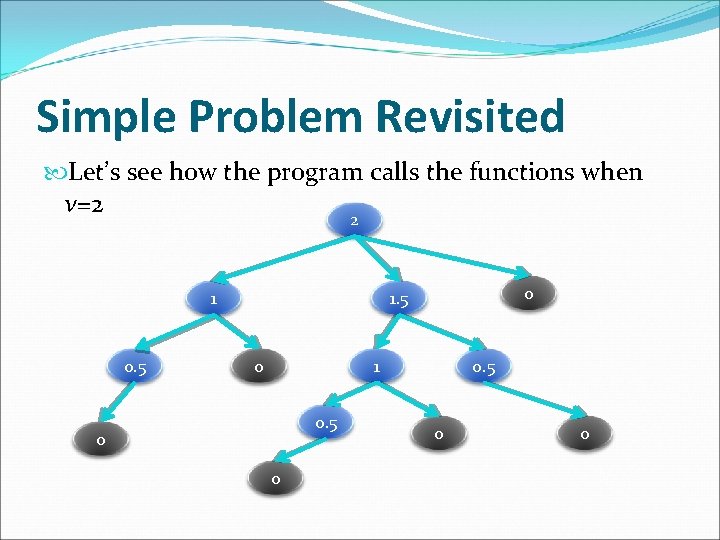
Simple Problem Revisited Let’s see how the program calls the functions when v=2 2 1 0. 5 0 0

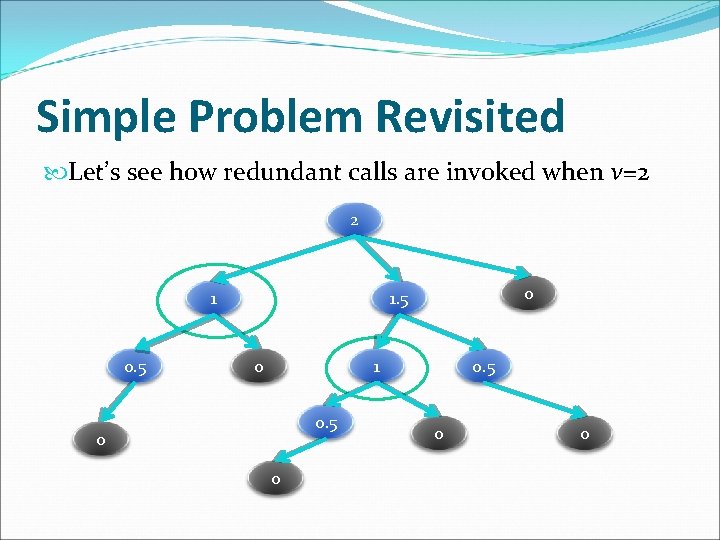
Simple Problem Revisited Let’s see how redundant calls are invoked when v=2 2 1 0. 5 0 0

Simple Problem Revisited Does two results for Count(1) differ? We see that invoking Count(1) from Count(2) and Count(1. 5) should give same result We call this Overlapping Sub-problems (重疊子問題) Why don’t we STORE the redundant calls?

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 V F(v) 0 1 0. 5 -1 1. 5 -1 2 -1

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 1 0. 5 0 0 V F(v) 0 1 0. 5 1 1 -1 1. 5 -1 2 -1

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 1 0. 5 0 0 V F(v) 0 1 0. 5 1 1 2 1. 5 -1 2 -1

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 1 0. 5 0 1 V F(v) 0 1 0. 5 1 1 2 1. 5 -1 2 -1

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 1 0. 5 0 1 0. 5 V F(v) 0 1 0. 5 1 1 2 1. 5 -1 2 -1

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 1 0. 5 0 0 1. 5 0 1 0. 5 V F(v) 0 1 0. 5 1 1 2 1. 5 3 2 -1

Simple Problem Revisited Why don’t we STORE the redundant calls? 2 1 0. 5 0 0 1. 5 0 1 0. 5 V F(v) 0 1 0. 5 1 1 2 1. 5 3 2 6

Simple Problem Revisited Why don’t we STORE the redundant calls? We call that Memo(r)ization The implementation strategy is Top-Down Performance?

Simple Problem Revisited �You have ∞ valued coins �They are $0. 5, $1, $2 and $5 respectively �Tell me how many ways I can make the total amount of N dollar(s) �Condition I: Count $1+$2 and $2+$1 are different �Condition II: Ignore repetitions

Simple Problem Revisited You have finite valued coins They are $0. 5, $1, $2 and $5 respectively Tell me how many ways I can make the total amount of N dollar(s) Condition I: Count $1+$2 and $2+$1 are different Condition II: Ignore repetitions

So far… We know that in solving DP questions it must have the following properties Overlapping Sub-problems

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di -8 5 10 Let me think about it -2 6 di-1 di 3 -4 -1 Hey, tell me the best answer if you are the end of the chain

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di -8 5 10 -2 Calculating… di-1

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di -8 5 10 I tell you, the best answer including me is 13 -2 6 di-1 di 3 -4 -1

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di -8 5 10 -2 6 di-1 di 3 -4 -1 If I include 13, my best answer should be 19 Otherwise 6

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di -8 5 10 -2 I tell you, the best answer including me is … 6 3 di di+1 -4 -1

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di We just ask the best answer that includes di-1 Why do we trust the best answer from di-1? Prove it by yourselves We call this property the optimal substructure (最 優子結構) Observing this property is somehow difficult Caution: Greedy also share this property!

Simple Problem Revisited II Diamond Chain [HKOJ 1010] When considering a diamond di We just ask the best answer that includes di-1 Why do we trust the best answer before di? Prove it by yourselves We call this property the memoryless property (無 後效性) Only the past event(s) determine the current event Observing this property is somehow difficult, too

Simple Problem Revisited II Variant What if we consider a RING? di: My neighbors could be my past events’ candidates!

So far… We know that in solving DP questions it must have the following properties Overlapping Sub-problems Optimal Substructure Memoryless

Next Step Sometimes I know a problem that consists of the required properties can be solved in DP, but… Memo(r)ization may cause Runtime Error due to stack overflow error Consider in problem I, N = 1, 000 I don’t know how to formulate

Next Step Sometimes I know a problem that consists of the required properties can be solved in DP, but… Memo(r)ization may cause Runtime Error due to stack overflow error Consider in problem I, N = 1, 000 In top down implementation, we request the previous events (formally, we call it states) Recall a nice property called memoryless We can compute all the previous states first, then determine the current Bottom Up approach

Next Step An event should be called a state How to describe a state is very important Wrong or insufficient info to describe the state would lead to wrong result e. g. if I want to predict the weather in a particular day, I must know the weather of previous day. So the date and its weather must both be present In problem I, how to describe the state?

Next Step An event should be called a state From previous examples, we know that there are relationships between past and current states In mathematical term, we call that state transition equation (狀態轉移方程) In words, we know that Count(N) is combining the case of all reducible values’ count. In mathematics,

Bottom Up Usually the procedure of bottom up implementation is. Algorithm Bottom-Up Begin For Any State N as current state For any previous state k If condition is satisfied then Transit state N from k End Bottom-Up Very often you may see lots of loops in DP solutions Usually transition takes place within the last loop Remember the base case!

Bottom Up Problem I, in bottom-up Algorithm Count Begin Let C[N], where C[0] = 1 For i : = 1 to N do For j : = {0. 5, 1, 2, 5} do If i – j >= 0 then C[i] += C[i-j]; End Count

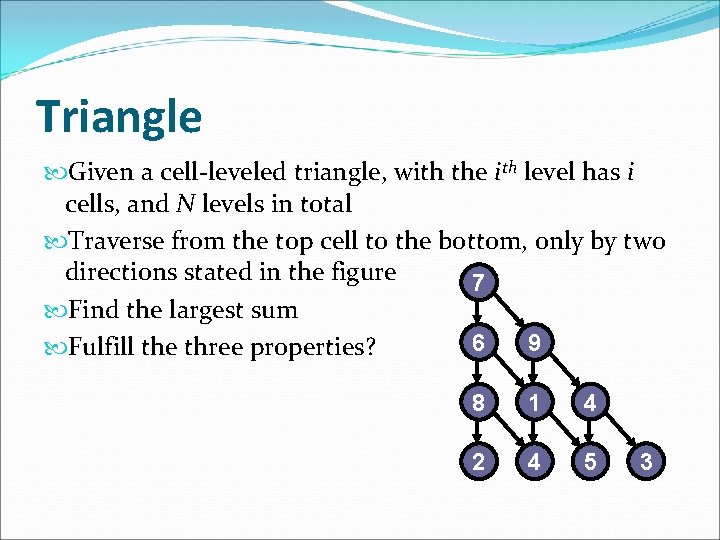
Triangle Given a cell-leveled triangle, with the ith level has i cells, and N levels in total Traverse from the top cell to the bottom, only by two directions stated in the figure 7 Find the largest sum 6 9 Fulfill the three properties? 8 1 4 2 4 5 3

Triangle Defining a state The ith level? The ith level, jth cell? What does a state store? If you don’t know, please refer to the task description again… Let S[i][j] stores the optimum value

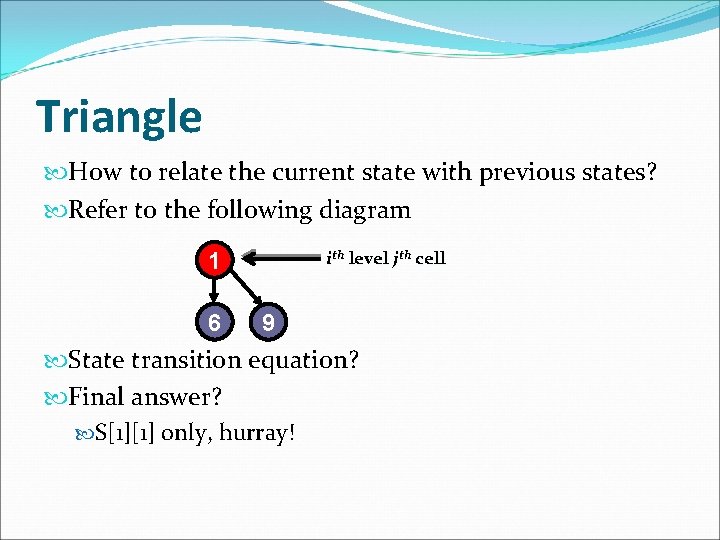
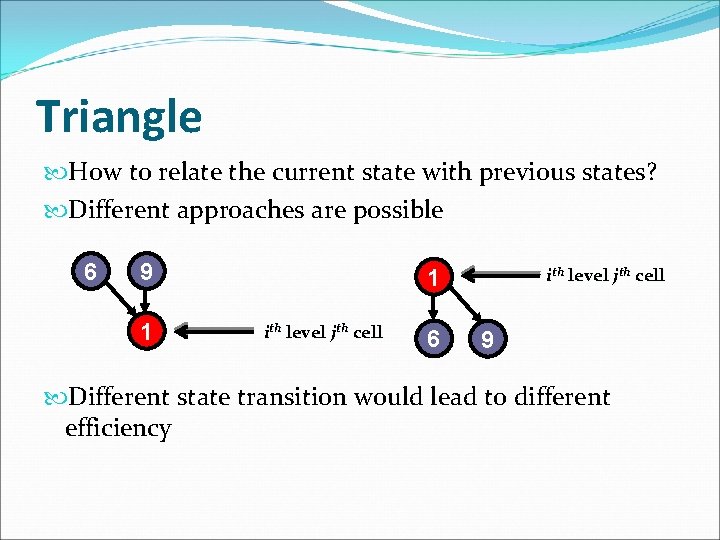
Triangle How to relate the current state with previous states? Refer to the following diagram 6 9 1 ith level jth cell State transition equation? Final answer? Every cell at the bottom can be the answer Need extra check

Triangle How to relate the current state with previous states? Refer to the following diagram 1 6 ith level jth cell 9 State transition equation? Final answer? S[1][1] only, hurray!

Triangle How to relate the current state with previous states? Different approaches are possible 6 9 1 1 ith level jth cell 6 ith level jth cell 9 Different state transition would lead to different efficiency

Edit Distance Given two strings A and B You can insert, delete or change a character to A Find the minimum changes made to transform A to B e. g. it takes 3 changes to transform “text” to “tree”

Edit Distance First, define the state (important!) Think of what makes an event Can we induce the past events? Bare in mind: those past events must be sufficient to determine the current state What are we assuming on previous states? The past states store the minimal change to transform a substring of A to a substring of B Formulation? More complex

Edit Distance Variants LCS (Longest Common Subsequence) Show me how you can transform it!

Non-spacious Writing You have to write an article, single paragraph You have typed N words in order, each word has length Wi Every word must have one space in between for separation Each line can only have at most L letters For each line, the unused space shows the emptiness by squaring its count Minimize the emptiness

Non-spacious Writing Example “HKOI” “is” “the” “goodest” “and” “fun” “: o)” A line can only have 7 letters at most Best layout H K O I I S T H E G O O D E S T A N D : F U N O ) Emptiness = 9 + 16 = 26

Non-spacious Writing Determine the state Is the number of line important? State transition equation? Constraints N < 1, 000 L < 100 Length of any word < L Algorithm? H K O I I S T H E G O O D E S T A N D : O ) F U N

Non-spacious Writing Considering in different order the previous states may lead to different complexities O(N 2) vs O(NL) Please think if your algorithm can pass the time limit and resources limit or not before implementing

Common Mode DP on rectangular array Again we use more memory as a trade off for time 以空間換取時間 DP on trees DP on ugly states Special representation on state is required

Optimization for DP If we need lots of different states, it probably implies More for-loops More space needed for a state State transition becomes expensive Cure? Memory Optimization – Rolling Array (滾動數組) Runtime Optimization

Challenging Problem 1 3 6 -8 -7 0 22 7 0 -1 1 -4 12 Turkish Roulette 0 12 A roulette of S slots Each slot has a number You are given B balls A ball occupies 2 slots Each ball has its number A slot can be occupied by one ball For each ball, let L be the sum of the two slots’ values times its number If the number on ball is negative, you gain $L, otherwise you lose $L -3 5 3 1

Challenging Problem 1 -4 12 12 3 1 6 -8 -7 0 22 7 0 -1 Turkish Roulette 0 A roulette of S slots Each slot has a number Xi You are given B balls Each ball has its number Yj Conditions: 3 < S < 250 1 < B < └S / 2┘ -64 < Xi, Yj < 64, for 1 < i < S, 1 < j < B Derive the solution by yourself! -3 5 3 1

Challenging Problem Painting [HKOI IOI/NOI TFT 2008 Q 3] N critical points Consecutive up-down-wave Minimize difference between up and down area Minimize total area for tie breaks

Practice Problems HKOJ 1010 – Diamond Ring HKOJ 1053 – Longest Common Substring HKOJ 1058 – The Triangle II

Last Words Learning DP should be Fun! The idea in solving a problem is very interesting Beneficial! You can deal with more types of problems Sorrow! Thinking how to solve is painful Suggestion Please understand this notes thoroughly in order to attend the next training

Q&A I hear and I forget. I see and I remember. I do and I understand.