Lecture 5 Dynamic Programming Outline Knapsack revisited How





![Pseudo-code Knapsack 1. Initialize a[i, 0] = 0, a[0, j] = 0 (Base Case) Pseudo-code Knapsack 1. Initialize a[i, 0] = 0, a[0, j] = 0 (Base Case)](https://slidetodoc.com/presentation_image/67de6fb3eb4e7d675477775d6dd3cc1f/image-8.jpg)
![Longest Common Subsequence • Input: two strings a[] = ‘ababcde’ and b[] = ‘abbecd’ Longest Common Subsequence • Input: two strings a[] = ‘ababcde’ and b[] = ‘abbecd’](https://slidetodoc.com/presentation_image/67de6fb3eb4e7d675477775d6dd3cc1f/image-9.jpg)
- Slides: 11

Lecture 5 Dynamic Programming

Outline • Knapsack revisited: How to output the optimal solution, and how to prove correctness? • Longest Common Subsequence • Maximum Independent Set on Trees.

Example 2 Knapsack Problem • There is a knapsack that can hold items of total weight at most W. There are now n items with weights w 1, w 2, …, wn. Each item also has a value v 1, v 2, …, vn. • Goal: Select some items to put into knapsack 1. Total weight is at most W. 2. Total value is as large as possible. • Output: the set of items to put into the Knapsack

Recall: States and Transition function • Example: Capacity W = 4, 3 items with (weight, value) = (1, 2), (2, 3), (3, 4). • States (sub-problems): What is the maximum value for a Knapsack with capacity j (= 0, 1, 2, 3, 4) and the first i (= 0, 1, 2, 3) items? • Use a[i, j] to denote this maximum value, we have a[i, j] = max a[i - 1, j - wi] + vi (item i in knapsack) a[i - 1, j] (item i not in knapsack)

Dynamic Programming Table • Example: Capacity W = 4, 3 items with (weight, value) = (1, 2), (2, 3), (3, 4). 0 1 2 3 4 0 0 0 1 0 2 2 2 0 2 3 5 5 3 0 2 3 5 6 +4

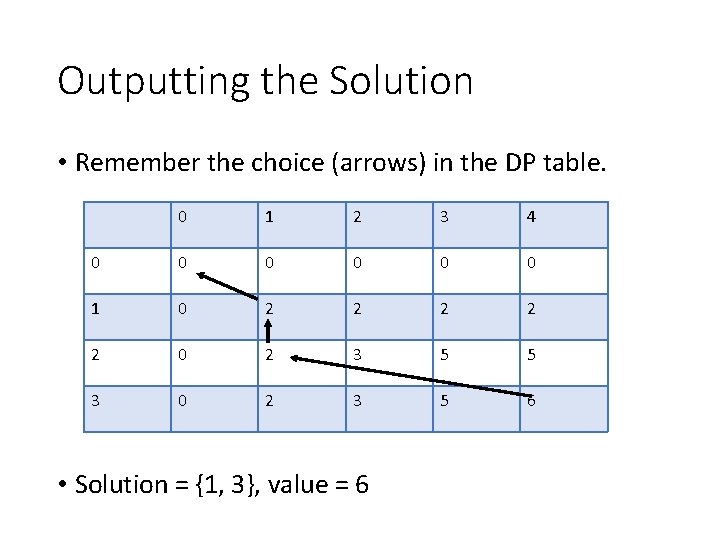
Outputting the Solution • Remember the choice (arrows) in the DP table. 0 1 2 3 4 0 0 0 1 0 2 2 2 0 2 3 5 5 3 0 2 3 5 6 • Solution = {1, 3}, value = 6

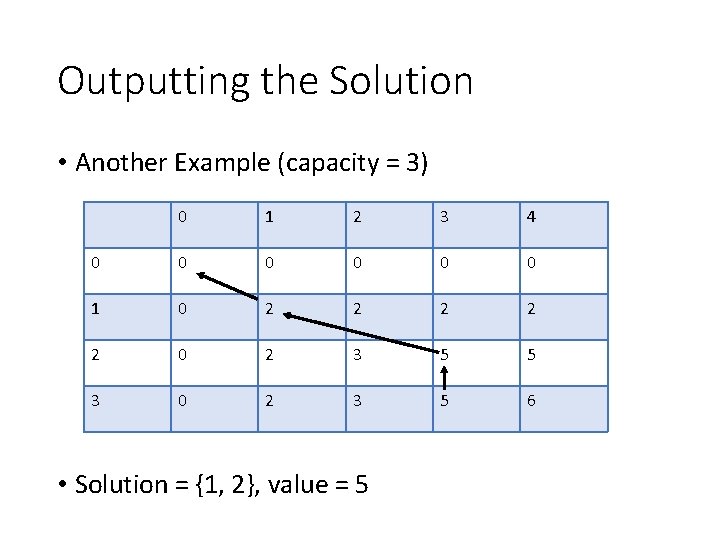
Outputting the Solution • Another Example (capacity = 3) 0 1 2 3 4 0 0 0 1 0 2 2 2 0 2 3 5 5 3 0 2 3 5 6 • Solution = {1, 2}, value = 5
![Pseudocode Knapsack 1 Initialize ai 0 0 a0 j 0 Base Case Pseudo-code Knapsack 1. Initialize a[i, 0] = 0, a[0, j] = 0 (Base Case)](https://slidetodoc.com/presentation_image/67de6fb3eb4e7d675477775d6dd3cc1f/image-8.jpg)
Pseudo-code Knapsack 1. Initialize a[i, 0] = 0, a[0, j] = 0 (Base Case) 2. FOR i = 1 to n (Enumerate #items) 3. FOR j = 1 to W (Enumerate capacity) 4. a[i, j] = a[i-1, j] (Case 1: not using item i) 5. IF j >= w[i] and a[i-1, j-w[i]] + v[i] > a[i, j] (if Case 2 is better) 6. a[i, j] = a[i-1, j-w[i]] + v[i] (Case 2: using item i) Output(n, W) 1. IF n = 0 or W = 0 THEN RETURN 2. IF a[n, W] = a[n-1, W] THEN 3. Output(n-1, W) 4. ELSE 5. Output(n-1, W-w[n]) 6. Print(n) (Case 1) (Case 2)
![Longest Common Subsequence Input two strings a ababcde and b abbecd Longest Common Subsequence • Input: two strings a[] = ‘ababcde’ and b[] = ‘abbecd’](https://slidetodoc.com/presentation_image/67de6fb3eb4e7d675477775d6dd3cc1f/image-9.jpg)
Longest Common Subsequence • Input: two strings a[] = ‘ababcde’ and b[] = ‘abbecd’ • Subsequence: same definition as in LIS (can skip characters) E. g. ‘abac’ is a subsequence of a[], but not b[] ‘abed’ is a subsequence of b[] but not a[] • Goal: Find the length of the longest common subsequence (LCS) In this example: LCS = ‘abbcd’, length = 5.

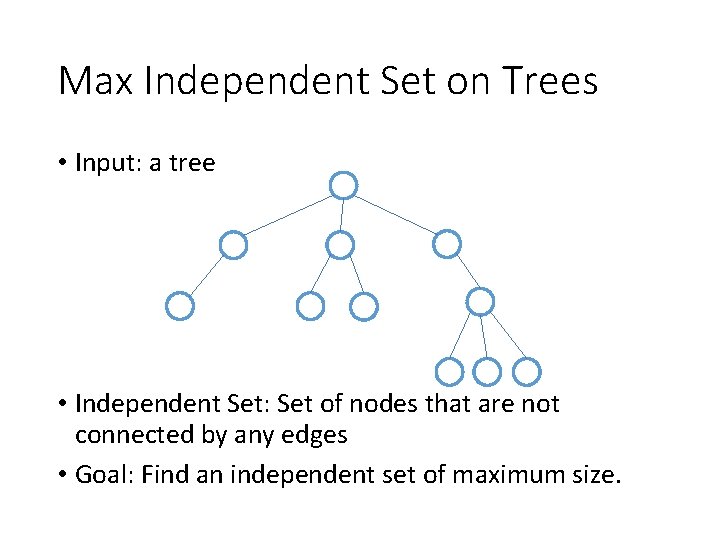
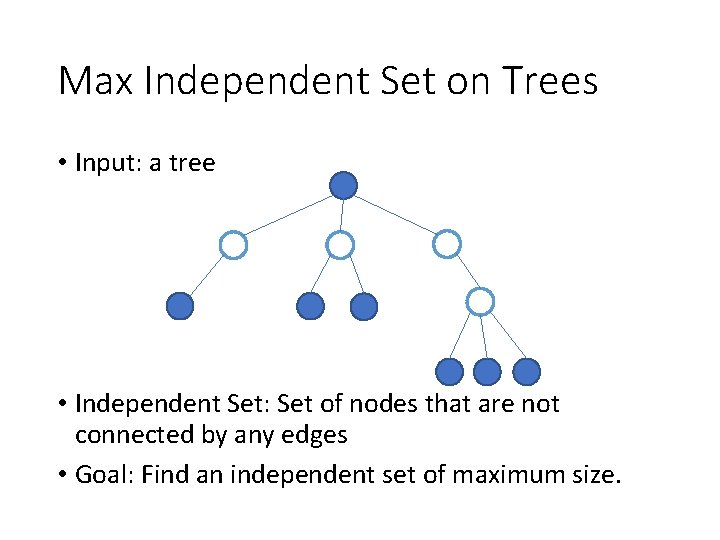
Max Independent Set on Trees • Input: a tree • Independent Set: Set of nodes that are not connected by any edges • Goal: Find an independent set of maximum size.

Max Independent Set on Trees • Input: a tree • Independent Set: Set of nodes that are not connected by any edges • Goal: Find an independent set of maximum size.