DYNAMIC PROGRAMMING GENERAL METHOD Dynamic Programming is an

DYNAMIC PROGRAMMING – GENERAL METHOD • Dynamic Programming is an algorithm design technique for optimization problems: often minimizing or maximizing. • Like divide and conquer, DP solves problems by combining solutions to sub-problems. • Unlike divide and conquer, sub-problems are not independent. – Sub-problems may share sub-problems • The term Dynamic Programming comes from Control Theory, not computer science. Programming refers to the use of tables (arrays) to construct a solution. • In dynamic programming we usually reduce time by increasing the amount of space • We solve the problem by solving sub-problems of increasing size and saving each optimal solution in a table (usually). • The table is then used for finding the optimal solution to larger problems. • Time is saved since each sub-problem is solved only once.

DYNAMIC PROGRAMMING – APPLICATIONS • • • MATRIC-CHAIN MULTIPLICATION OPTIMAL BINARY SEARCH TREES 0/1 KNAPSACK PROBLEM ALL PAIRS SHORTEST PATH PROBLEM TRAVELLING SALES PERSON PROBLEM RELIABILITY DESIGN

MATRIC-CHAIN MULTIPLICATION • Given : a chain of matrices {A 1, A 2, …, An}. • Once all pairs of matrices are parenthesized, they can be multiplied by using the standard algorithm as a sub-routine. • A product of matrices is fully parenthesized if it is either a single matrix or the product of two fully parenthesized matrix products, surrounded by parentheses. • For example, if the chain of matrices is {A, B, C, D}, the product A, B, C, D can be fully parenthesized in 5 distinct ways: (A ( B ( C D ))), (A (( B C ) D )), ((A B ) ( C D )), ((A ( B C )) D), ((( A B ) C ) D ).

MATRIC-CHAIN MULTIPLICATION • Example: A[30][35], B[35][15], C[15][5] minimum of A*B*C A*(B*C) = 30*35*5 + 35*15*5 = 7, 585 (A*B)*C = 30*35*15 + 30*15*5 = 18, 000 • Dynamic programming – time complexity of Ω(n 3) and space complexity of Θ(n 2).

OPTIMAL BINARY SEARCH TREES • OBST is one special kind of advanced tree. • It focus on how to reduce the cost of the search of the BST. • It may not have the lowest height ! • It needs 3 tables to record probabilities, cost, and root. • The case of search are two situations, one is success, and the other, without saying, is failure. • We can get the first statement : (i=1~n) ∑ pi + (i=0~n) ∑ qi = 1

OPTIMAL BINARY SEARCH TREES • For i 1 to n+1 do e[i, i-1] qi-1 do w[i, i-1] qi-1 For l 1 to n do for i 1 to n-l +1 do j i+l-1 e[i, j] ∞ w[i, j] w[i, j-1]+pj+qj For r i to j do t e[i, r-1]+e[r+1, j]+w[i, j] if t<e[i, j] then e[i, j] t root [i, j] r Return e and root

0/1 KNAPSACK PROBLEM • Given some items, pack the knapsack to get the maximum total value. Each item has some weight and some value. Total weight that we can carry is no more than some fixed number W. • So we must consider weights of items as well as their values. • Given a knapsack with maximum capacity W, and a set S consisting of n items • Each item i has some weight wi and benefit value bi (all wi and W are integer values) • The problem is called a “ 0 -1” problem, because each item must be entirely accepted or rejected.

0/1 KNAPSACK PROBLEM for w = 0 to W V[0, w] = 0 for i = 1 to n V[i, 0] = 0 for i = 1 to n for w = 0 to W if wi <= w // item i can be part of the solution if bi + V[i-1, w-wi] > V[i-1, w] V[i, w] = bi + V[i-1, w- wi] else V[i, w] = V[i-1, w] // wi > w

ALL PAIRS SHORTEST PATH PROBLEM • Consider a shortest path pijm from vi to vj such that |pijm| ≤ m i. e. , path pijm has at most m edges. • no negative-weight cycle all shortest paths are simple m is finite m ≤ n – 1 • i = j |pii|= 0 & ω(pii) = 0 • -1 i ≠ j decompose path pijm into pikm-1 & vk → vj , where|pikm |≤ m - 1 pikm-1 should be a shortest path from vi to vk by optimal substructure property. • Therefore, δ (vi , vj ) = δ (vi , vk ) + ωk j

ALL PAIRS SHORTEST PATH PROBLEM • • • given W = D 1 , compute a series of matrices D 2, D 3, . . . , Dn-1 , where Dm = ( dijm ) for m = 1, 2, . . . , n-1 final matrix Dn-1 contains actual shortest path weights, i. e. , dijn-1 = δ (vi , vj ) SLOW-APSP( W ) D 1 ← W for m ← 2 to n-1 do Dm ← EXTEND( Dm-1 , W ) return Dn-1 EXTEND ( D , W ) D = ( d ij ) is an n x n matrix for i ← 1 to n do for j ← 1 to n do d ij ← ∞ for k ← 1 to n do d ij ← min{d ij , d ik + ωk j} return D

TRAVELLING SALES PERSON PROBLEM d(i, j) = (direct) distance between city i and city j. The constraint basically says that x is a permutation of the cities (1, 2, 3, …, n) Make sure that you appreciate the role of { } in this formulation.

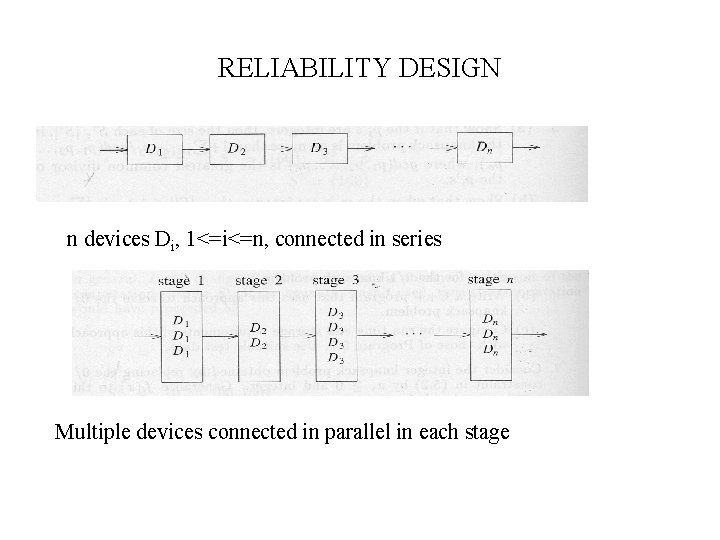
RELIABILITY DESIGN • • • Solve a problem with a multiplicative optimization function Several devices are connected in series ri be the reliability of device Di Reliability of the entire system Duplicate : multiple copies of the same device type are connected in parallel use switching circuits

RELIABILITY DESIGN n devices Di, 1<=i<=n, connected in series Multiple devices connected in parallel in each stage