Differential Calculus The derivative or derived function of







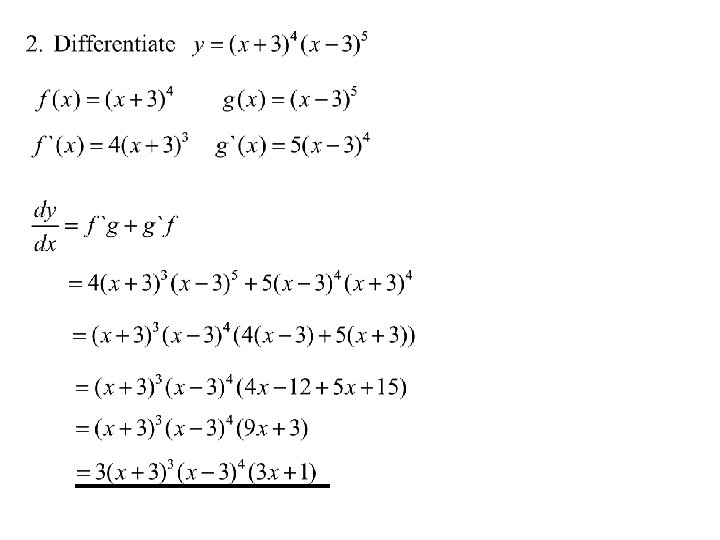



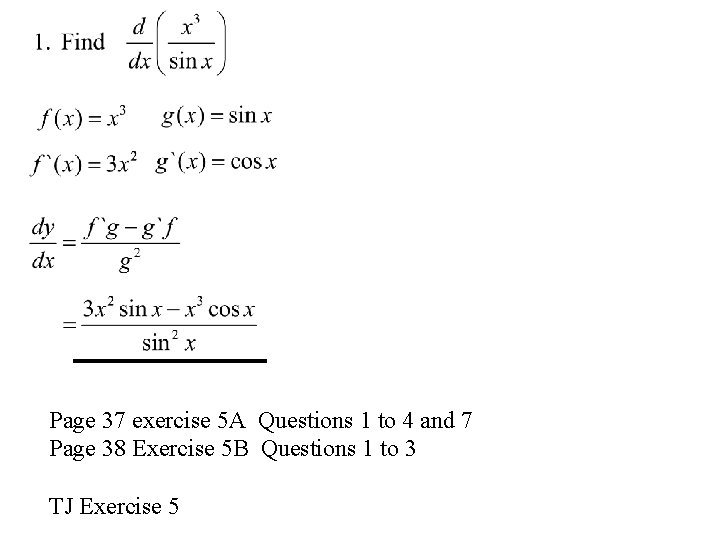


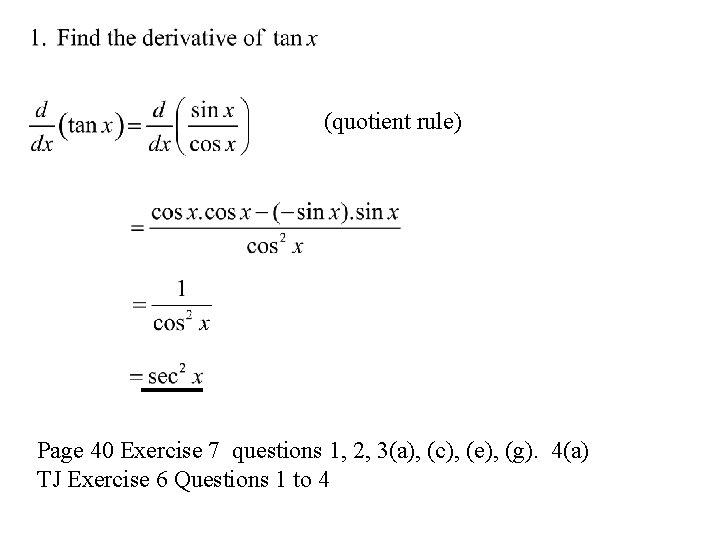
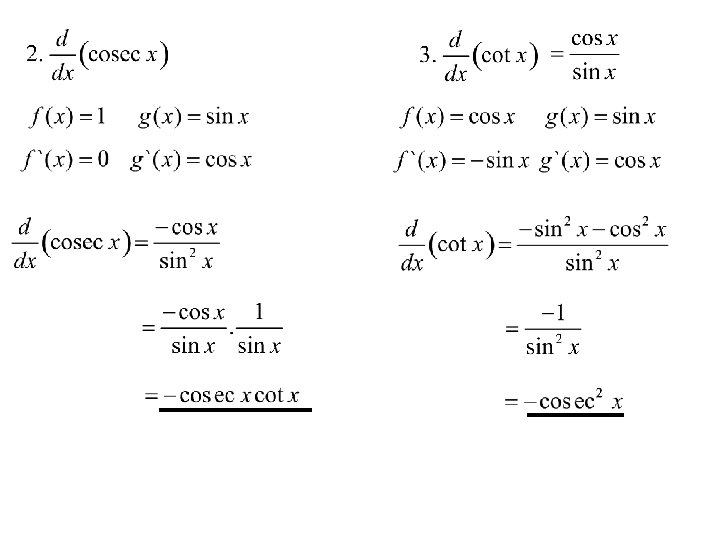



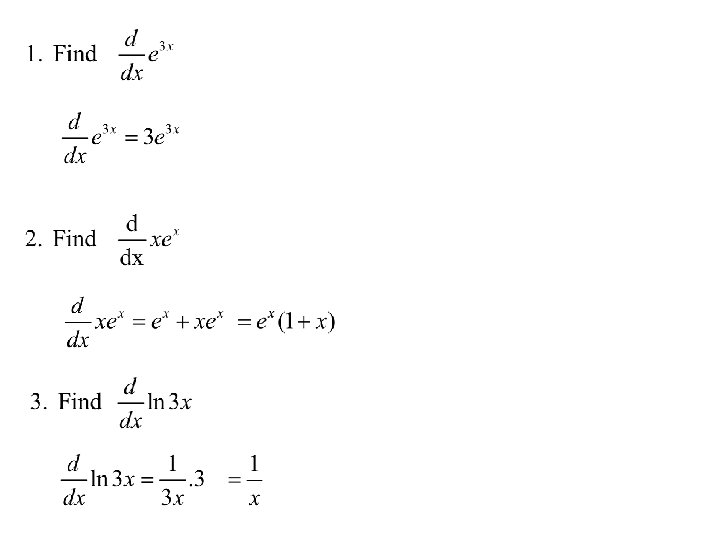
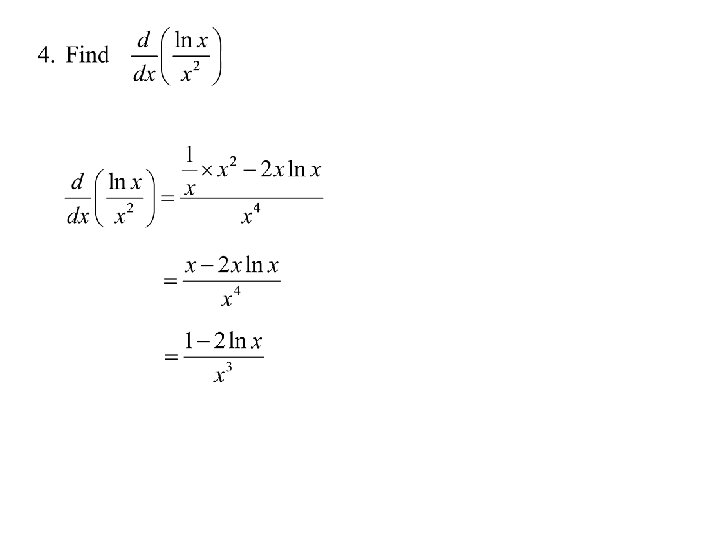


















- Slides: 42

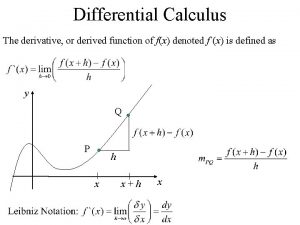
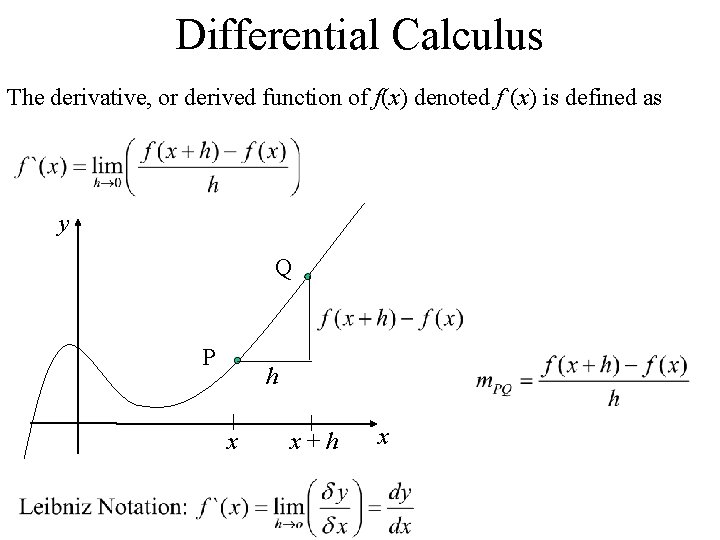
Differential Calculus The derivative, or derived function of f(x) denoted f`(x) is defined as y Q P h x x+h x

Differentiation from first principles Given that f(x) is differentiable, we can use the definition to prove that if


Further practice on page 29 Exercise 1 A Questions 1, 4, 5 and 7 TJ Exercise 1 But not just Yet……. .

CAUTION Not all functions are differentiable. y = tan(x). Here, tan(x) has ‘breaks’ in the graph where the gradient is undefined y x Although the graph is continuous, the derivative at zero is undefined as the left derivative is negative and the right derivative is positive. For a function to be differentiable, it must be continuous.

Further practice on page 29 Exercise 1 A Questions 1, 4, 5 and 7 TJ Exercise 1 Differentiation reminder: Page 32 Exercise 3 A Questions 1(a), (d), 2(a), (c), (d) 3(a), 4(a), 6(a) TJ Exercise 2 TJ Exercise 3

The Product Rule Using Leibniz notation, OR

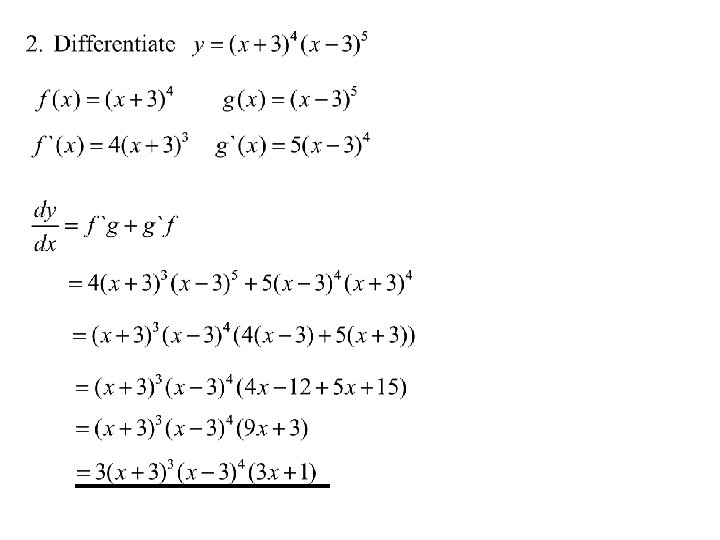


Page 35 exercise 4 A Questions 1, 2(b) and 3 Page 36 exercise 4 B Questions 1(b), 3 and 4 TJ Exercise 4

The Quotient Rule Using Leibniz notation, OR
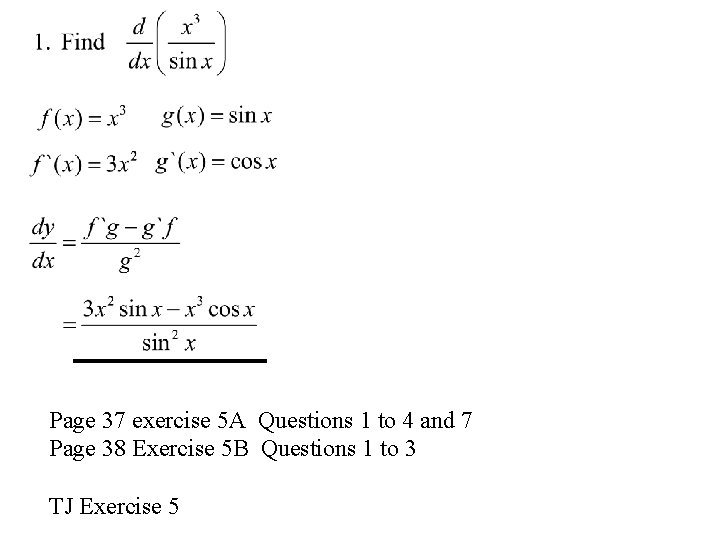
Page 37 exercise 5 A Questions 1 to 4 and 7 Page 38 Exercise 5 B Questions 1 to 3 TJ Exercise 5

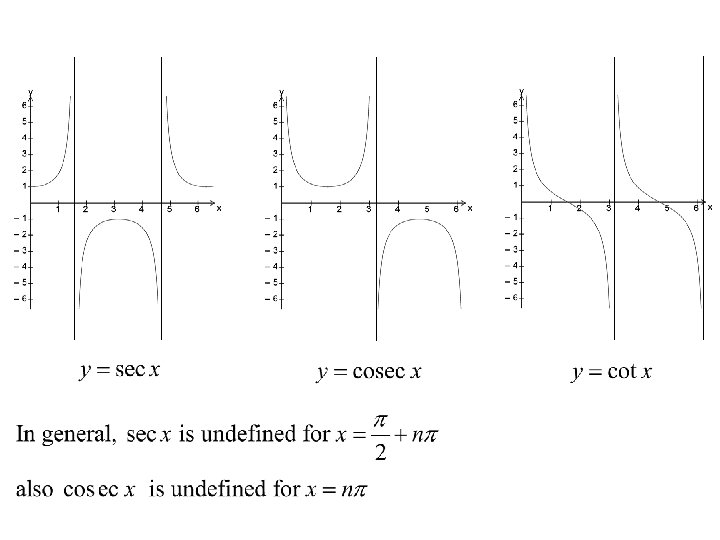
Sec, Cosec, cot and tan Unlike the sine and cosine functions, the graphs of sec and cosec functions have ‘breaks’ in them. The functions are otherwise continuous but for certain values of x, are undefined.


undefined
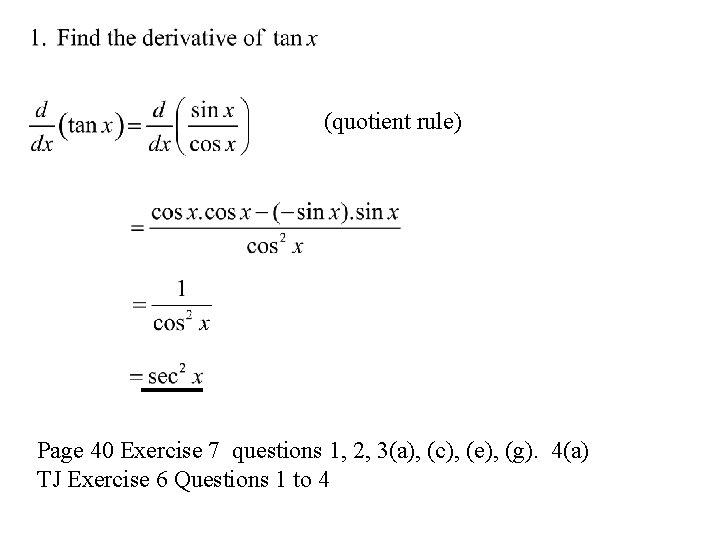
(quotient rule) Page 40 Exercise 7 questions 1, 2, 3(a), (c), (e), (g). 4(a) TJ Exercise 6 Questions 1 to 4
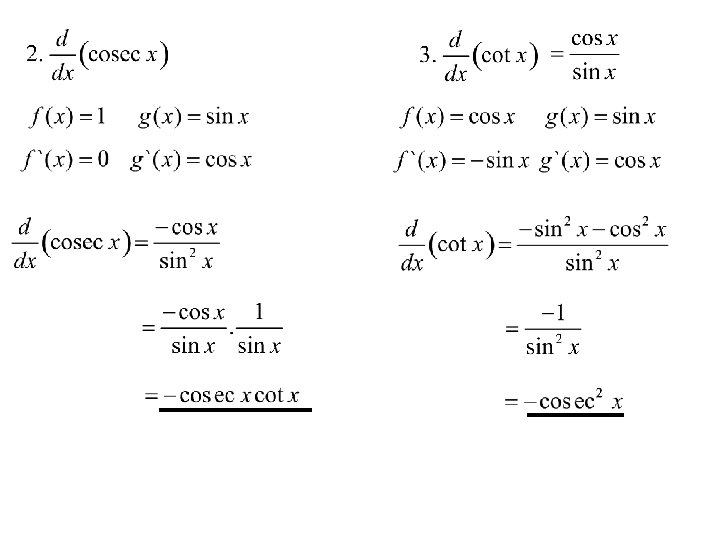

Exponential and Logarithmic functions

Proof 1. Let us examine this limit. When a approaches e, the limit approaches 1.

Proof 2. Differentiating both sides with respect to x. Using the chain rule.
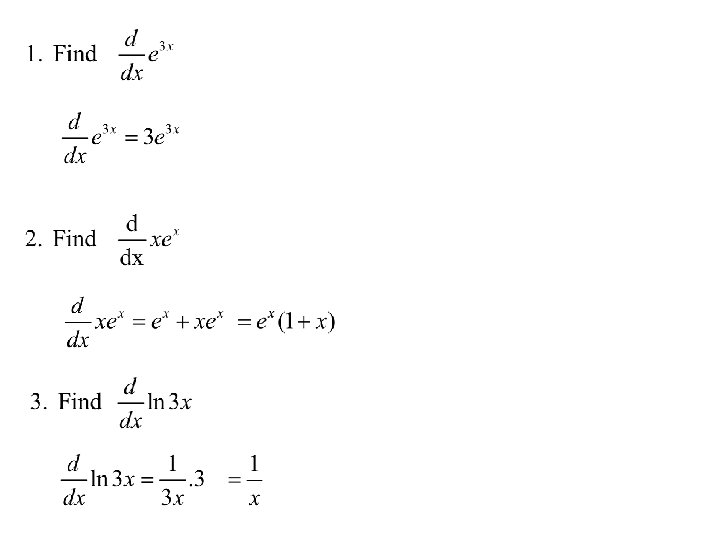
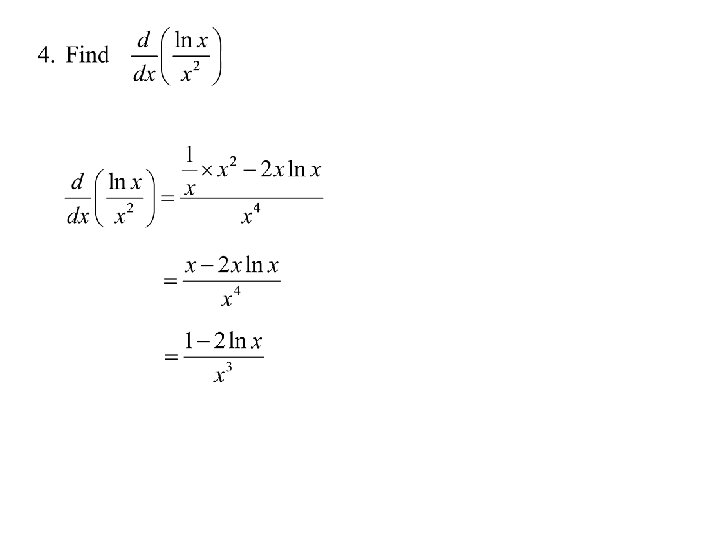

Higher derivatives Function 1 st derivative etc. 2 nd Derivative………. . nth Derivative

Page 43 Exercise 8 A Questions 1(b), (d), 2(b), (c), (d), 3(a), (b), (c). 4(d), (e), 5(a), (c), (e), 6(b), (c), (e) TJ Exercise 6 Page 46 Exercise 9 A Qu. 1 to 6 Review Chapter 2. 1

Applications of Differential Calculus Let displacement from an origin be a function of time. Velocity is a rate of change of displacement. Acceleration is a rate of change of velocity. Note: The use of units MUST be consistent.

A particle travels along the x axis such that x(t) = 4 t 3 – 2 t + 5, where x represents its displacement in metres from the origin ‘t’ seconds after observation began. (a) How far from the origin is the particle at the start of observation? (b) Calculate the velocity and acceleration of the particle after 3 seconds. Hence the particle is 5 m from the origin at the start of the observation.

A body travels along a straight line such that S = t 3 – 6 t 2 + 9 t + 1, where S represents its displacement in metres from the origin after observation began. (a) (b) (c) (d) Find when (i) the velocity and (ii) the acceleration is zero. When is the distance S increasing? When is the velocity of the body decreasing? Describe the motion of the particle during the first 4 seconds of observation.

The velocity is zero when t = 1 or 3 seconds. The acceleration is zero when t = 2 seconds.

(b) S is increasing when This occurs when the graph of above the x axis is Hence the distance S is increasing when t < 1 and when t > 3 seconds. (c) V is decreasing when Hence the velocity is decreasing when t < 2 seconds.

At t = 0, the particle is 1 m from the origin with a velocity of 9 ms-1 decelerating at a rate of 12 ms-2. At t = 1, the particle is 5 m from the origin at rest decelerating at a rate of 6 ms-2. At t = 2, the particle is 3 m from the origin with a velocity of -3 ms-1 with zero acceleration. At t = 3, the particle is 1 m from the origin at rest accelerating at a rate of 3 ms-2. At t = 4, the particle is 5 m from the origin with a velocity of 9 ms-1 accelerating at a rate of 12 ms-2.

Page 51 Exercise 1 Questions 1(a), (b), (d), (f), 2(a), (c), (e), 3, 4, 6, 7, 8, 10, 12. TJ Exercise 7.

Extreme Values of a Function (Extrema) Critical Points A critical point of a function is any point (a, f(a)) where f `(a) = 0 or where f `(a) does not exist.

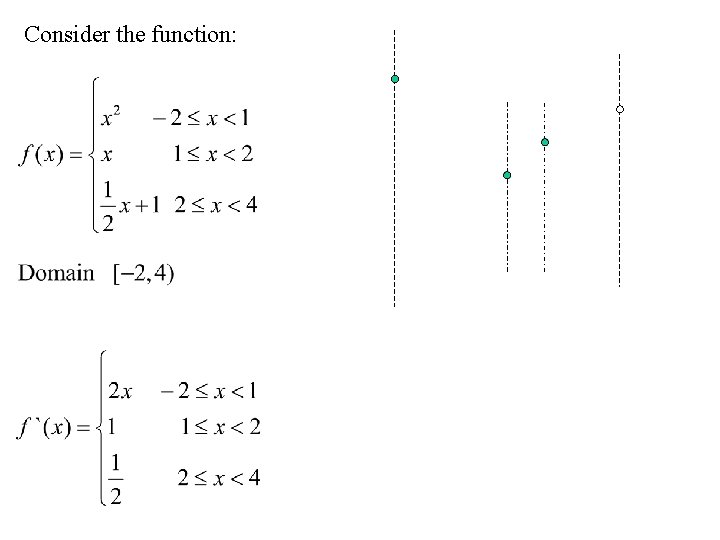
Consider the function:

Critical points are: A E D C B A (-2, 4) f `(-2) does not exist. (Right differentiable at x = -2) B (0, 0) f `(0) = 0. (Turning point) C (1, 1) f `(1) does not exist. Left derivative =2, right derivative = 1 D (2, 2) f `(2) does not exist. Left derivative = 1, right derivative = 0. 5 E is not a critical point as it is not in the domain of f.

Local extrema Local extreme values occur either at the end points of the function, turning points or critical points within the interval of the domain. Consider the function, 3 is the local maximum value -1 is the local minimum value If extrema occurs at end points then they are end point maximums or end point minimums.

In short, (i) Local maximum / minimum turning points (ii) End point values (iii) Critical points The Nature of Stationary Points. If f `(a) = 0 then a table of values over a suitable interval centred at a provides evidence of the nature of the stationary point that must exist at a. A simpler test does exist. It is the second derivative test.

If the second derivative test is easier to determine than making a table of signs then this provides an efficient technique to finding the nature of stationary points. Page 56 Exercise 2 Questions 1, 3(a), (c), (e), (g), (i) Page 60 Exercise 3 Questions 1(a), (c), (e), 5(a) to (d) TJ Exercise 8

Optimisation Problems Optimisation problems appear in many guises – often in the context in which they are set can be somewhat misleading. 1. Read the question at least TWICE. 2. Draw a sketch where appropriate. This should help you introduce any variables you are likely to need. It may be that you come back to the diagram to add in an extra ‘x’ etc. 3. Try to translate any information in the question into a mathematical statement. 4. Identify the variables to be optimised and then express this variable as a function of one of the other variables. 5. Find the critical numbers for the function arrived at in step 4. 6. Determine the local extrema and if necessary the global extrema.

1. An open box with a rectangular base is to be constructed from a rectangular piece of card measuring 16 cm by 10 cm. A square is to be cut out from each corner and the sides folded up. Find the size of the cut out squares so that the resulting box has the largest possible volume. 16 – 2 x x x 10 – 2 x (max / min V occurs when = 0)

Hence the cut out squares should be 2 cm in length.

Page 63 Exercise 4 A. Note Question 8 can’t be done but try to prove me wrong!! Page 64 Exercise 4 B is VERY Difficult. (VERY) TJ Exercise 9
 What is fundamental theorem
What is fundamental theorem Divergence de gradient
Divergence de gradient Carrying capacity equation calculus
Carrying capacity equation calculus Differential calculus functions
Differential calculus functions Differentiation formulas
Differentiation formulas The derivative of a function
The derivative of a function Differentiability implies continuity example
Differentiability implies continuity example Chain rule derivative
Chain rule derivative Inverse function
Inverse function Log and exponential derivatives
Log and exponential derivatives The derivative of a function
The derivative of a function Exponential differentiation
Exponential differentiation Differentiating inverse trigonometric functions
Differentiating inverse trigonometric functions Derivative of exponential function
Derivative of exponential function Chain rule derivative
Chain rule derivative Hyperbolic trig derivatives
Hyperbolic trig derivatives Bessels equation
Bessels equation Bessel differential equation
Bessel differential equation Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Thang điểm glasgow
Thang điểm glasgow Chúa yêu trần thế alleluia
Chúa yêu trần thế alleluia Các môn thể thao bắt đầu bằng tiếng đua
Các môn thể thao bắt đầu bằng tiếng đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tiính động năng
Công thức tiính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ 101012 bằng
101012 bằng Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ V. c c
V. c c Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể