Clculo Numrico Mdulo V Resoluo Numrica de Sistemas

Cálculo Numérico Módulo V Resolução Numérica de Sistemas Lineares – Parte I Profs. : Bruno Correia da Nóbrega Queiroz José Eustáquio Rangel de Queiroz Marcelo Alves de Barros

Sistemas Lineares n Forma Geral onde: aij xi bi coeficientes incógnitas termos independentes 2

Sistemas Lineares n Exemplo 01 2, 4, -5, 4, 1, -5, 2, 4 e 5 coeficientes x 1, x 2 e x 3 incógnitas 5, 2 e -1 termos independentes 3

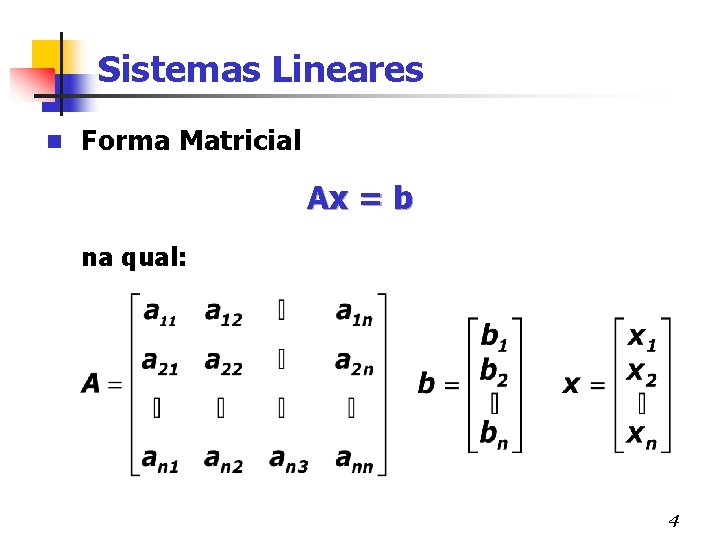
Sistemas Lineares n Forma Matricial Ax = b na qual: 4

Sistemas Lineares n Exemplo 02 4 Forma Geral 4 Forma Matricial 5

Sistemas Lineares n Classificação I 4 Impossível Não possui solução l Exemplo 03 6

Sistemas Lineares n Classificação II 4 Possível Possui 1 ou mais soluções l Determinado Solução única t Exemplo 04 7

Sistemas Lineares n Classificação III 4 Possível Possui 1 ou mais soluções l Indeterminado Mais de uma solução t Exemplo 05 8

Sistemas Lineares n Classificação IV 4 Possível Possui 1 ou mais soluções l Homogêneo Vetor b=0 (x=0 sempre existe solução) t Exemplo 06 9

Sistemas Lineares n Sistemas Triangulares: 4 Possibilidade de resolução de forma Direta l Inferior 10

Sistemas Lineares n Sistemas Triangulares: 4 Possibilidade de resolução de forma Retroativa l Superior 11

Solução Retroativa n Exemplo 7: 4 Dado o sistema: 4 Primeiro passo para sua resolução: 12

Solução Retroativa n Exemplo 7: 4 Segundo passo: 4 Terceiro passo: 13

Solução Retroativa n Exemplo 7: 4Último passo: 14

Métodos Numéricos n Diretos 4 Solução pode ser encontrada a partir de um número finito de passos l Método de Gauss l Método da Eliminação de Jordan l Fatoração LU 15

Métodos Numéricos n Iterativos 4 Solução a partir de uma seqüência de aproximações para o valor do vetor solução x , até que seja obtido um valor que satisfaça à precisão pré-estabelecida l Método de Jacobi l Método de Gauss – Seidel 16

Método de Gauss n Propósito 4 Transformação do sistema linear a ser resolvido em um sistema linear triangular; triangular 4 Resolução do sistema linear triangular de forma retroativa 17

Método de Gauss n Transformação do Sistema Linear 4 Troca da ordem das linhas; 4 Multiplicação de uma das equações por um número real não nulo; 4 Substituição de uma das equações por uma combinação linear dela mesma com outra equação. 18

Método de Gauss n Passos do Método de Gauss 4 Construção da matriz aumentada Ab 19

Método de Gauss n Passos do Método de Gauss 4 Passo 1: l Eliminar os coeficientes de x 1 presentes nas linhas 2, 3, . . . , n - sendo a 21 = a 31, =. . . = an 1 = 0 - sendo a 11 chamado de pivô da coluna l Substituir a linha 2, L 2, pela combinação linear 20

Método de Gauss n Passos do Método de Gauss 4 Substituir a linha 3, L 3, pela combinação linear: 21

Método de Gauss n Passos do Método de Gauss 4 Continuar a substituição até a linha n; 4 Caso algum elemento app=0, achar outra linha k onde akp≠ 0 e trocar tais linhas. Caso a linha k não exista, o sistema linear não possui solução. 22

Método de Gauss n Passos do Método de Gauss 4 Eliminar os coeficientes de x 2 nas linhas 3, 4, . . . , n (fazer a 32=a 42=. . . =an 2 = 0); 4 Eliminar os coeficientes de x 3 nas linhas 4, 5, . . . , n (fazer a 43=a 53=. . . =an 3 = 0) e assim sucessivamente. 23

Método de Gauss n Exemplo 8: 4 Resolver o sistema: l Matriz aumentada Ab 24

Método de Gauss n Exemplo 8: 4 Faz-se: 4 Assim: 25

Método de Gauss n Exemplo 8: 4 Faz-se: 4 Assim: 26

Método de Gauss n Exemplo 8: 4 Obtém-se a matriz: 27

Método de Gauss n Exemplo 8: 4 Substituindo a linha 3 por: 4 Têm-se: 28

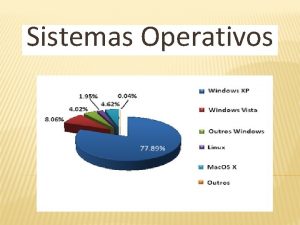
Método de Gauss n Exemplo 8: 4 A matriz [Ab] fica assim com os seguintes valores: 29

Método de Gauss n Exemplo 8: 4 Usa-se a solução retroativa: 30

Método de Gauss n Exemplo 9: 4 Resolver o sistema. 4 Representando aumentada: o sistema pela matriz 31

Método de Gauss n Exemplo 9: 4 Escolhendo a primeira linha como pivô, obtém-se: 32

Método de Gauss n Exemplo 9: 4 Representando o sistema pela matriz aumentada: 33

Método de Gauss n Exemplo 9: 4 Escolhendo agora a segunda linha como pivô, têm-se: 34

Método de Gauss n Exemplo 9: 4 Obtêm-se a seguinte matriz ampliada: 35

Método de Gauss n Exemplo 9: 4 O que termina com a triangulação: 36

Método de Gauss n Exemplo 9: 4 Com solução: x 3 = -3, 9888/3, 3463=-1, 1918 x 2 =[ -16, 3 - (-4, 74) (-1, 1920)]/(-12, 82) = 1, 7121 x 1 = [10 - 5, 4(1, 7122) - 3, 3(-1, 1920)]/1, 5 = 3, 1251 37

Método do Pivoteamento Parcial n Semelhante ao método de Gauss; n Minimiza a amplificação de erros de arredondamento durante as eliminações; n Consiste em escolher o elemento de maior módulo em cada coluna para ser o pivô. 38

Método do Pivoteamento Parcial n Exemplo 10: 4 Resolver o sistema com precisão de 4 casas decimais 39

Método do Pivoteamento Parcial n Exemplo 10: 4 Matriz aumentada original deve ser ajustada: 40

Método do Pivoteamento Parcial n Exemplo 10: 4 Sistema inalterado, elemento pivô 4, 2 4 Encontrar as novas linhas: 41

Método do Pivoteamento Parcial n Exemplo 10: 4 A matriz ampliada fica da forma: 4 Como o elemento coluna, tem-se: já é o pivô da 2ª 42

Método do Pivoteamento Parcial n Exemplo 10: 4 A matriz ampliada fica na forma: 43

Método do Pivoteamento Parcial n Exemplo 10: 4 A solução do sistema triangular que resultou dessas operações é: x 3 = -3, 9886/3, 3463 = -1, 1919 x 2 = [5, 8214 -1, 6929 (-1, 1919)]/(4, 5786) = 1, 7121 x 1 = [11, 7 - 2, 3(1, 7121)- 4, 5(-1, 1919)]/4, 2 = 3, 1252 44

Método do Pivoteamento Parcial Exemplo 9: Exemplo 10 (com pivoteamento): x 3 = -1, 1918 x 2 = 1, 7121 x 1 = 3, 1252 x 3 = -1, 1919 x 2 = 1, 7121 x 1 = 3, 1251 Solução encontrada no Matlab: x 1 = -1, 19198135 x 2 = 1, 71216783 x 3 = 3, 12522144522145 45

Método de Jordan n Consiste em efetuar operações sobre as equações do sistema, com a finalidade de obter um sistema diagonal equivalente; n Um sistema diagonal é aquele em que os elementos aij da matriz coeficiente [A] são iguais a zero, para i≠j, ≠j i, j = 1, 2, . . . , n. 46

Método de Jordan n Sistema diagonal equivalente: 47

Método de Jordan n Exemplo 11: 4 A partir do sistema: 4 Com matriz aumentada: 48

Método de Jordan n Exemplo 11: 4 Substituindo a linha 2 por: 4 Substituindo a linha 3 por : 49

Método de Jordan n Exemplo 11: 4 A matriz ampliada resulta em: 4 Substituindo a linha 3 por: 50

Método de Jordan n Exemplo 11: 4 A matriz ampliada resulta em: 4 Substituindo a linha 2 por 51

Método de Jordan n Exemplo 11: 4 Matriz ampliada resulta em: 4 Substituindo a linha 1 por 52

Método de Jordan n Exemplo 11: 4 Substituindo a linha 1 por: 4 A matriz ampliada fica da seguinte forma: 53

Método de Jordan n Exemplo 11: 4 E as soluções são: l x 1 =-2, 556 , x 2= -0, 285, x 3=4, 783 54

Decomposição em LU n O objetivo é fatorar a matriz dos coeficientes A em um produto de duas matrizes L e U. 4 Seja: 55

Decomposição em LU n E a matriz coeficiente A: 4 Tem-se, então: 56

Decomposição em LU n Para se obter os elementos da matriz L e da matriz U, deve-se calcular os elementos das linhas de U e os elementos da colunas de L como segue. 57

Decomposição em LU n 1ª linha de U: Faze-se o produto da 1ª linha de L por todas as colunas de U e a iguala com todos os elementos da 1ª linha de A, assim: 58

Decomposição em LU n 1ª coluna de L: Faz-se o produto de todas as linhas de L, (da 2ª a até a nª), pela 1ª coluna de U e a iguala com os elementos da 1ª coluna de A, (abaixo da diagonal principal), principal obtendo , 59

Decomposição em LU n 2ª linha de U: Faz-se o produto da 2ª linha de L por todas as colunas de U, (da 2ª até a nª), e igualando com os elementos da 2ª linha de A, (da diagonal principal em diante), diante obtêm-se , 60

Decomposição em LU n 2ª coluna de L: Faz-se o produto de todas as linhas de L (da 3ª até a nª) pela 2ª coluna de U e a iguala com os elementos da 2ª coluna de A, (abaixo da diagonal principal), principal obtendo , 61

Decomposição em LU n Temos a seguinte fórmula geral: 62

Decomposição em LU n Resumo de Passos: 4 Seja um sistema Ax = b de ordem n, onde A satisfaz as condições da fatoração LU. 4 Então, o sistema Ax = b pode ser escrito como: l LUx = b 63

Decomposição em LU n Resumo dos Passos: 4 Fazendo Ux = y, a equação acima reduzse a Ly = b. b 4 Resolvendo o sistema triangular inferior Ly = b, b obtém-se o vetor y. 64

Decomposição em LU n Resumo dos Passos: 4 Substituição do valor de y no sistema Ux = y Obtenção de um sistema triangular superior cuja solução é o vetor x procurado; 4 Aplicação da fatoração LU na resolução de sistemas lineares Necessidade de solução de dois sistemas triangulares 65

Erros - Avaliação de Erros n No sistema A x = b , no qual: o erro da solução é x – x’. 66

Erros - Avaliação de Erros n Procedimento de Determinação do Erro 4 Determinar: l A x’ = b’ 67

Erros – Resíduo n Procedimento de Determinação do Erro 4 Fazer: l Resíduo = b – b’ = A x - A x’ = A (x – x’) = A erro 68

Erros – Resíduo n Verifica-se que: 4 O resíduo não é o erro, apenas uma estimativa do mesmo; 4 Quanto menor for o resíduo, menor será o erro. 69

Erros – Resíduo n Exemplo 12: 4 Refinar a solução do sistema: 4 Cuja solução encontrada através pelo método de Gauss, utilizando a solução retroativa é: 70

Erros – Resíduo n Exemplo 12: 4 O resíduo calculado é: 4 Vê-se pelo resíduo que a precisão alcançada não foi satisfatória. 4 O vetor x(0) é chamado de vetor solução 71

Erros – Resíduo n Exemplo 12: 4 Com o intuito de melhorar a solução, considera-se um novo vetor x(1) chamado de vetor solução melhorado 72

Erros – Resíduo n Exemplo 12: 4 De forma que : x(1) = x(0) + δ(0), onde δ(0) é o vetor de correção Assim: 73

Erros – Resíduo n Exemplo 12: 4 Calcular o vetor de correção: 74

Erros – Resíduo n Exemplo 12: 4 A solução é: 75

Erros – Resíduo n Exemplo 12: 4 Desta forma, a solução melhorada será: 76

Erros – Resíduo n Exemplo 12: 4 Cujo novo resíduo é: 77

Erros – Resíduo n Exemplo 12: 4 Em exemplos onde o resíduo ainda não seja satisfeito pode-se utilizar o mesmo procedimento: x(2)=x(1)+δ(1) 4 Assim, o vetor correção δ(1), será calculado por A δ(1) =r(1). 78

Erros – Resíduo n Exemplo 12: 4 Acha-se assim, sempre uma solução melhorada e com resíduo tendendo a zero. 79

Sistemas Lineares - Bibliografia 4 Ruggiero, M. A. Gomes & Lopes, V. L. da R. Cálculo Numérico: Aspectos teóricos e computacionais. MAKRON Books, 1996, 2ª ed. 4 Asano, C. H. & Colli, E. Cálculo Numérico: Fundamentos e Aplicações. Departamento de Matemática Aplicada – IME/USP, 2007. 4 Sanches, I. J. & Furlan, D. C. Métodos Numéricos. DI/UFPR, 2006. 4 Paulino, C. D. & Soares, C. Erros e Propagação de Erros, Notas de aula, SE/ DM/ IST [Online] http: //www. math. ist. utl. pt/stat/pe/qeb/semestr e_1_2004 -2005/PE_erros. pdf [Último acesso 07 de Junho de 2007]. 80