SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Área Académica: Ingeniería Mecánica Profesor: Ing. Francisco Javier Barrera González. Periodo: Julio – Diciembre 2016

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Resumen • Los alumnos necesitan saber resolver sistemas de ecuaciones lineales de varias variables por diferentes métodos, para aplicarlos a problemas reales. Abstract • Students need to know how to solve systems of linear equations of several variables by different methods to apply them to real problems. Keywords: Linear equations.

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES • Un sistema de ecuaciones es un conjunto de ecuaciones con las mismas incógnitas. • Un sistema de ecuaciones lineales es un sistema de ecuaciones en el que cada ecuación es lineal. • Una solución de un sistema es una asignación de valores para las incógnitas que hace verdadera cada una de las ecuaciones. • Resolver un sistema significa determinar todas las soluciones del sistema.

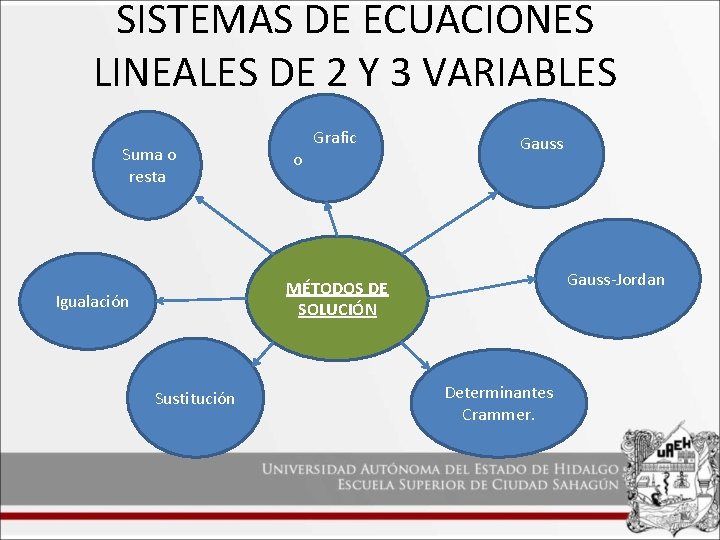
SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Suma o resta o Grafic Gauss-Jordan MÉTODOS DE SOLUCIÓN Igualación Sustitución Determinantes Crammer.

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES MÉTODO GRAFICO • EJEMPLO. Resuelve por el método grafico el sistema: X – 2 y = 10 Ec. (1) 2 X + 3 y = – 8 Ec. (2) De la Ec. (1): si X = 0 entonces ahora si y = 0 : -2 y = 10 X = 10 y = 10 /(-2) y = -5

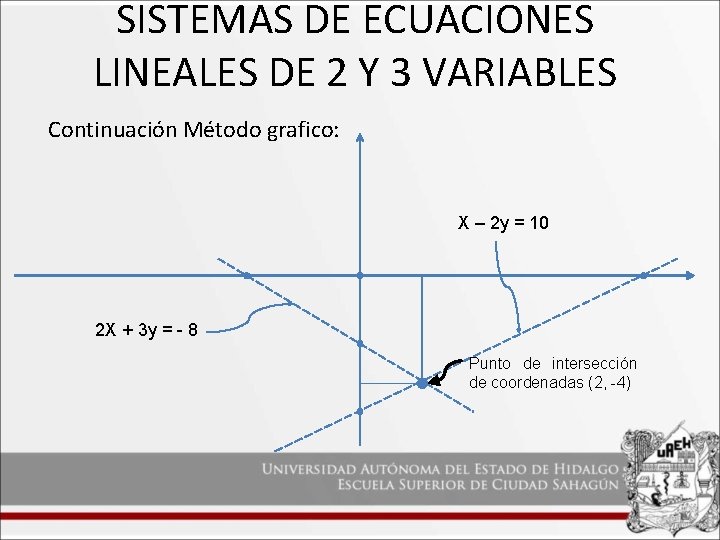
SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método grafico: De la Ec. (2): si X = 0 entonces ahora si y = 0 : 3 y = -8 2 X = - 8 y = - 8 /3 X = -8 /2 X=-4 Estos valores representan líneas con la intersección en los ejes, donde se intersectan estas dos rectas así definidas es la solución la sistema.

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método grafico: X – 2 y = 10 2 X + 3 y = - 8 Punto de intersección de coordenadas (2, -4)

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES MÉTODO DE SUMA O RESTA (REDUCCIÓN). Consiste en modificar las ecuaciones del sistema, de tal manera que se igualen en valor absoluto los coeficientes de una de las incógnitas y tenga signos contrarios, por lo que al sumarse algebraicamente las ecuaciones se elimina una de las incógnitas, generando una ecuación lineal con una incógnita que es fácil de resolver. EJEMPLO. Resolver el sistema: 4 X + 6 Y = - 3 Ec. (1) 5 X + 7 Y = - 2 Ec. (2)

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Multiplicamos la Ec. (1) por 5 y la Ec. (2) por (-4), y sumamos los resultados de las operaciones anteriores: 5 ( 4 X + 6 Y = – 3 ) 20 X + 30 Y = – 15 – 4 ( 5 X + 7 Y = – 2 ) – 20 X – 28 Y = 8 2 Y = – 7 Por lo tanto : Y = – 7 /2 Ahora sustituyendo el valor de (Y) en cualquier de las ecuaciones originales, obtenemos: 5 X + 7 (– 7 /2 ) = – 2 5 X – 49/2 =– 2

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método Suma o Resta (reducción). 5 X = – 2 + (49/2) = 45/2 Por lo tanto X = (45/2) / 5 = 45/10 X=9/2 De modo que: X=9/2 Y = – 7 /2

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método Suma o Resta (reducción). 5 X = – 2 + (49/2) = 45/2 Por lo tanto X = (45/2) / 5 = 45/10 X=9/2 De modo que: X=9/2 Y = – 7 /2

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Método de Igualación. Éste método consiste en desarrollar los siguientes pasos: 1. Despejar la misma incógnita en cada una de las ecuaciones del sistema dado. 2. Se igualan entre sí las expresiones obtenidas, de tal forma eliminamos una de las incógnitas y quedando una ecuación con una incógnita. 3. Resolvemos la ecuación de primer grado resultante. 4. Se sustituye el valor determinado en cualquiera de las ecuaciones originales para obtener el valor de la otra incógnita.

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES EJEMPLO: Resolver el siguiente sistema. Método de igualación 6 X + 2 Y = – 10 9 X + 4 Y = – 24 Despejando (Y) en ambas ecuaciones, nos da: 2 Y = – 10 – 6 X 4 Y = – 24 – 9 X Y = (– 10 – 6 X)/2 Y = (– 24 – 9 X)/4 Igualando entre si ambas expresiones, obtenemos: (– 10 – 6 X)/2 = (– 24 – 9 X)/4 4 (– 10 – 6 X) = 2(– 24 – 9 X)

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método de igualación. – 40 – 24 X = – 48 – 18 X – 24 X + 18 X = – 48 + 40 – 6 X= – 8 X = (– 8 / – 6) X = 4/3 Sustituyendo el valor de (X) en cualquiera de las ecuaciones originales, obtenemos: 9(4/3) + 4 Y = – 24

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método de igualación. 12 + 4 Y = – 24 – 12 4 Y = – 36 Y = (– 36 / 4) Y=– 9

SISTEMAS DE ECUACIONES LINEALES DE 2 Y 3 VARIABLES Continuación Método de igualación. 12 + 4 Y = – 24 – 12 4 Y = – 36 Y = (– 36 / 4) Y=– 9

SISTEMAS DE ECUACIONES LINEALES DE DOS VARIABLES MÉTODO DE SUSTITUCIÓN. Resolver un sistema por éste método, realizamos los siguientes pasos: 1. Despejamos en cualquiera de los sistemas de ecuaciones una de las incógnitas en términos de la otra. 2. Se sustituye la expresión para la incógnita despejada en la otra ecuación que no se ha utilizado; se obtiene una ecuación con una incógnita. 3. Se resuelve la ecuación de primer grado resultante. 4. Se sustituye el valor determinado en cualquiera de las ecuaciones original para determinar el valor de la otra incógnita.

SISTEMAS DE ECUACIONES LINEALES DE DOS VARIABLES EJEMPLO METODO DE SUSTITUCIÓN: Resolver el sistema de ecuaciones: 7 X – 4 Y = 5 Ec. (1) 9 X + 8 Y = 13 Ec. (2) De la Ec. (1) despejamos la “Y” en términos de X: – 4 Y = 5 – 7 X Y = [(5 – 7 X)/(– 4)] Sustituimos éste valor en la Ec. (2), originando una ecuación de una incógnita. 9 X + 8 [(5 – 7 X)/(– 4)] = 13

SISTEMAS DE ECUACIONES LINEALES DE DOS VARIABLES Continuación MÉTODO DE SUSTITUCIÓN: 9 X – 10 + 14 X = 13 9 X + 14 X = 13 + 10 23 X = 23 X=1 Sustituyendo el valor obtenido de X en cualquiera de las ecuaciones originales, determinamos: 7 (1) – 4 Y = 5 – 7 Y = (– 2) /(– 4) Y = 1/2

SISTEMAS DE ECUACIONES LINEALES DE DOS VARIABLES NOTA: Para comprobar la solución de cualquiera de los métodos anteriores sólo basta con sustituir los valores obtenidos de las incógnitas en las ecuaciones originales del sistema, si las igualdades se cumplen entonces la solución es correcta.

Referencias James Stewart, Lothar Redlin, Saleem watson (y L. Devore (2012). Precálculo Matemáticas para el cálculo. Cengage Learning, México 6° edición.