Diferenciacin e Integracin numrica Programacin Numrica Diferenciacin La

Diferenciación e Integración numérica Programación Numérica

Diferenciación La diferenciación numérica puede calcularse usando la definición de derivada Tomando una h pequeña. Si h > 0 se llama fórmula de diferencia progresiva, si h < 0 se llama fórmula de diferencia regresiva.

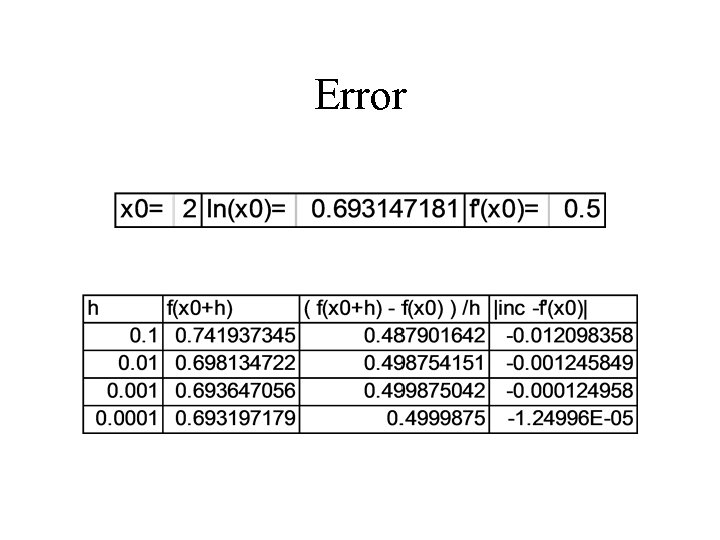
Error

Preguntas rápidas Obtenga la derivada de las siguientes funciones en el punto especificado utilizando Excel o Matlab. Compárelas con el valor obtenido analíticamente. 1. f(x) = 3 x sen(2 x), x = p/6 2. f(x) = 5 ln(x + 1) – x 2/5, x = 1. 2

Fórmulas de diferencias divididas hacia adelante Primera derivada Segunda derivada Tercera derivada

Fórmulas de diferencias divididas centradas Primera derivada Segunda derivada Tercera derivada

Fórmulas de diferencias divididas hacia atrás Primera derivada Segunda derivada Tercera derivada

Ejemplo f (x) = – 0. 1 x 4 – 0. 15 x 3 – 0. 5 x 2 – 0. 25 x+1. 2

Datos no espaciados regularmente Para derivar datos no espaciados regularmente se utiliza la siguiente fórmula. Se requiere conocer la función en tres puntos.

Ejemplo El flujo de calor en la interfaz suelo-aire puede calcularse con la ley de Faraday Donde q = flujo de calor, k = coeficiente de difusividad térmica (3. 5 x 10 -7), r = la densidad del suelo (1800), C = calor específico del suelo (840). 10 12 13. 5 Aire Suelo 1. 25 = – 1. 333 q = 70. 56 3. 75

Integración numérica A los métodos de integración se les llama cuadratura numérica. Seleccionaremos un conjunto de nodos [x 0, . . . , xn] del intervalo [a, b]. Después integramos un polinomio interpolante de Lagrange Se obtiene: Donde

Regla del trapecio Utilizando un polinomio interpolante lineal de Lagrange. Donde h = x 1 – x 0 = Esta fórmula vale cuando f(x) tiene valores positivos. P 1 f Da valores exactos para polinomios de grado 1. x 0 = a x 1 = b

Pregunta rápida Muestre que se cumple la regla del trapecio

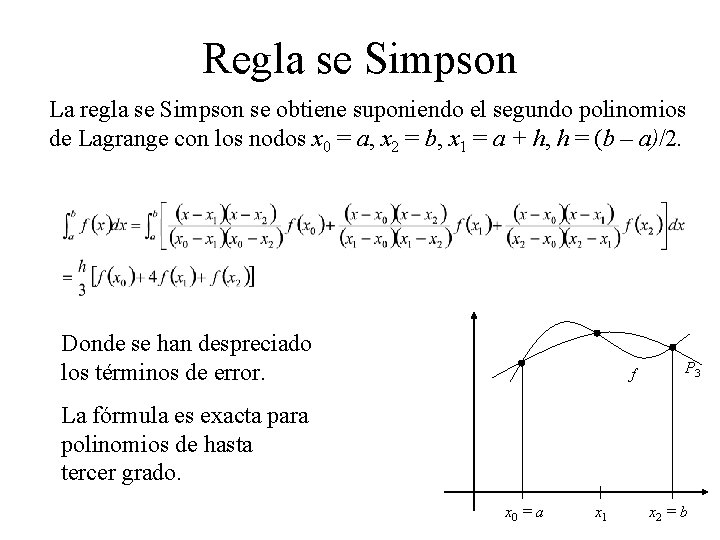
Regla se Simpson La regla se Simpson se obtiene suponiendo el segundo polinomios de Lagrange con los nodos x 0 = a, x 2 = b, x 1 = a + h, h = (b – a)/2. Donde se han despreciado los términos de error. f P 3 La fórmula es exacta para polinomios de hasta tercer grado. x 0 = a x 1 x 2 = b

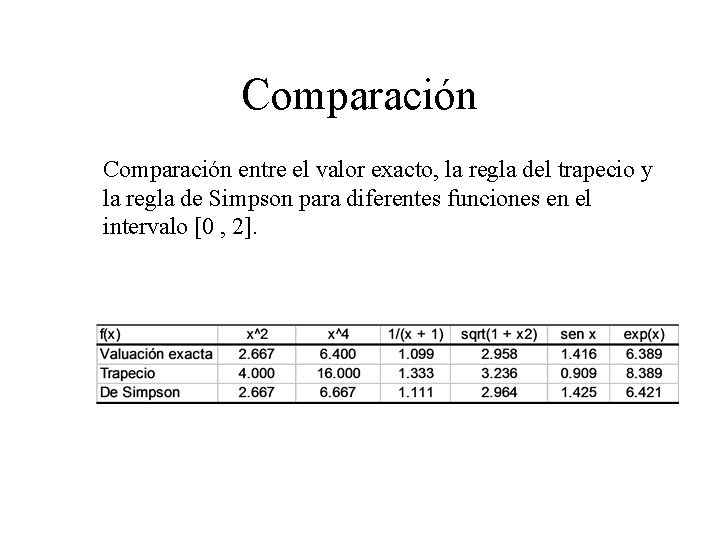
Comparación entre el valor exacto, la regla del trapecio y la regla de Simpson para diferentes funciones en el intervalo [0 , 2].

Regla de Simpson 3/8 Ajustando polinomios de Lagrange de orden 3 usando cuatro puntos se llega a la regla de Simpson de 3/8 También puede expresarse por: Esta regla es útil cuando el número de puntos es impar.

Integración numérica compuesta Integrando ex por Simpson en [0, 4] El error es: 53. 59815 – 56. 76958 = – 3. 17143 Separando en dos integrales:

Dividiendo en 4 intervalos El error es: 53. 59815 – 53. 61622 = – 0. 01807

Regla compuesta de Simpson Teorema. Sea f C 4[a, b], n par, h = (b – a)/n, y xj = a + jh para cada j = 0, 1, 2, . . . n. La regla de Simpson para n subintervalos puede escribirse como: y= f(x) x 0 = a x 2 j-1 x 2 j+1 xn = b

Regla compuesta del trapecio Teorema. Sea f C 4[a, b], n par, h = (b – a)/n, y xj = a + jh para cada j = 0, 1, 2, . . . n. La regla del trapecio para n subintervalos puede escribirse como: y= f(x) x 0 = a x 1 xj-1 xj xn– 1 xn = b

Regla compuesta del punto medio Teorema. Sea f C 4[a, b], n par, h = (b – a)/(n+2), y xj = a + (j+1)h para cada j = – 1, 0, 1, 2, . . . n+1. La regla de compuesta del punto medio para n subintervalos puede escribirse como: y= f(x) x 0 = a x 0 x 1 xj-1 xj xj+1 xn xn+1 = b

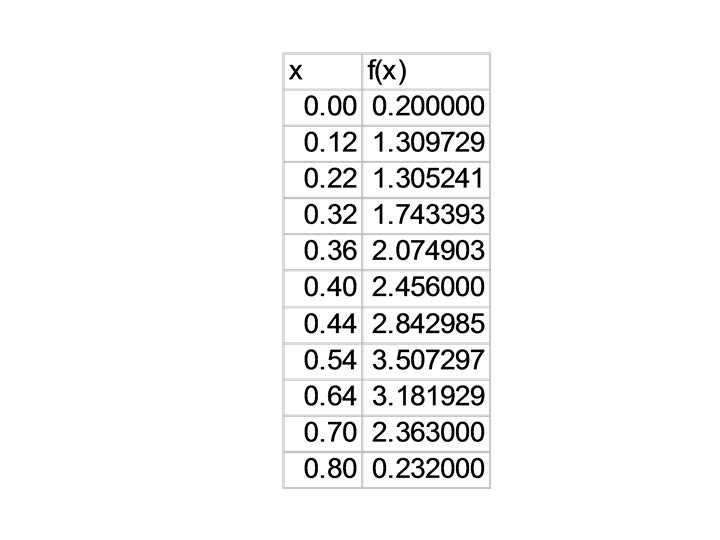
Datos con espaciamiento irregular Si los datos están espaciados de forma irregular, como en el caso de datos experimentales, la integración puede llevarse a cabo mediante la aplicación de la regla del trapecio a cada subintervalo. Donde hi = ancho del segmento i.

Ejemplo Determinar la distancia recorrida para los datos siguientes: t min 1 2 3. 25 4. 5 6 7 8 9 9. 5 10 V m/s 5 6 5. 5 7 8. 5 8 6 7 7 5 t = [1 2 3. 25 4. 5 6 7 8 9 9. 5 10]; v = [5 6 5. 5 7 8. 5 8 6 7 7 5]; suma = 0; for i=2: length(t) suma = suma + (t(i)-t(i-1))*(v(i-1)+v(i))/2; end suma ans = 60. 3750

Algoritmos Regla del trapecio Algoritmos para la regla del trapecio de uno solo segmento function trap(h, f 0, f 1) trap = h*(f 0+f 1)/2 end Algoritmos para la regla del trapecio de múltiples segmentos function trap(h, n, f) sum = f 0; for i = 1, n– 1 sum = sum + 2*fi end sum = sum + fn trap = h*sum/2 end

Algoritmos Regla simple de Simpson Regla de Simpson de 1/3 function simp 13(h, f 0, f 1, f 2) simp 13 = 2*h*(f 0+4*f 1+f 2)/6 end Regla de Simpson de 3/8 function simp 38(h, f 0, f 1, f 2, f 3) simp 38 = 3*h*(f 0+3*f 1+3*f 2+f 3)/8 end

Regla de Simpson 1/3 múltiple Function simp 13 m(h, n, f) sum = f 0 for i = 1, n– 2, 2 sum = sum+4*fi+2*fi+1 end sum = sum+4 fn-1+fn simp 13 m = h*sum/3 end

Algoritmos Regla compuesta de Simpson Regla de Simpson de número de segmentos pares o impares function simpint(a, b, n, f) h = (b-a)/n if n=1 then sum=trap() else m = n odd = n/2 -int(n/2) if odd>0 and n>1 then sum = sum + simp 38(h, fn-3, fn-2, fn-1, fn) m = n-3 end if m>1 then sum = sum + simp 13 m(h, m, f) end simpint = sum end

Ejemplo Trapecio Sea la siguiente función: f (x) = 0. 2 + 25 x – 200 x 2 + 675 x 3 – 900 x 4 + 400 x 5 Integrada en el intervalo de a = 0 a b = 0. 8 con trapecio: Valor real I = 1. 64053333 f (a) = 0. 2000 f (b) = 0. 2320 I = h (f (b) – f (a) )/2 0. 17280000 error = 89. 47%

Ejemplo Simpson 1/3 Sea la siguiente función: f (x) = 0. 2 + 25 x – 200 x 2 + 675 x 3 – 900 x 4 + 400 x 5 Integrada en el intervalo de a = 0 a b = 0. 8 con trapecio: Valor real I = 1. 64053333 f (a) = 0. 2 f ((a+b)/2) = 2. 456 f (b) = 0. 232 I = 0. 8 (0. 2+4(2. 456)+0. 232)/6 = 1. 36746667 error = 16. 6%

Ejemplo Simpson 3/8 Sea la siguiente función: f (x) = 0. 2 + 25 x – 200 x 2 + 675 x 3 – 900 x 4 + 400 x 5 Integrada en el intervalo de a = 0 a b = 0. 8 con trapecio: Valor real I = 1. 64053333 f (0) = 0. 2 f (0. 26667) = 1. 432724 f (0. 5333) = 3. 487177 f (0. 8) = 2. 232 I = 0. 8 (0. 2+3(1. 432724+3. 487177)+ 2. 232 )/8 = 1. 519170 error = 7. 4%

Ejemplo Simpson 1/3 y Simpson 3/8 Sea la siguiente función: f (x) = 0. 2 + 25 x – 200 x 2 + 675 x 3 – 900 x 4 + 400 x 5 Integrada en el intervalo de a = 0 a b = 0. 8 con 5 segmentos, con trapecio 2 primeros y Simpson los 3 últimos: Valor real I = 1. 64053333 f (0) = 0. 2 f (0. 16) = 1. 29692 f (0. 32) = 1. 74339 f (0. 48) = 3. 18601 f (0. 64) = 3. 18193 f (0. 8) = 0. 23200 Simpson 1/3: I 1/3 = 0. 32*(0. 2 +4(1. 29692)+ 1. 74339 )/6 = 0. 3803237 Simpson 3/8 I 3/8 = 0. 48 (1. 74339 +3(3. 18601 + 3. 18193 )+ 2. 232 )/8 = 1. 264754 I = 1. 645077 error = 0. 28%