Modelado Matemtico de Sistemas Fsicos Resolucin de Sistemas

Modelado Matemático de Sistemas Físicos Resolución de Sistemas de Ecuaciones No Lineales • En esta clase, trataremos la resolución mixta simbólica y numérica de sistemas de ecuaciones no lineales acopladas. • El método de rasgadura brinda también una solución eficiente para el tratamiento de sistemas de ecuaciones no lineales. • La iteración numérica de los sistemas de ecuaciones no lineales puede limitarse a las variables de rasgadura. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Contenido • • Febrero 5, 2008 Sistemas de ecuaciones no lineales Iteración de Newton con rasgadura Iteración de Newton de sistemas de ecuaciones lineales © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Sistemas de Ecuaciones No Lineales: Ejemplo I Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

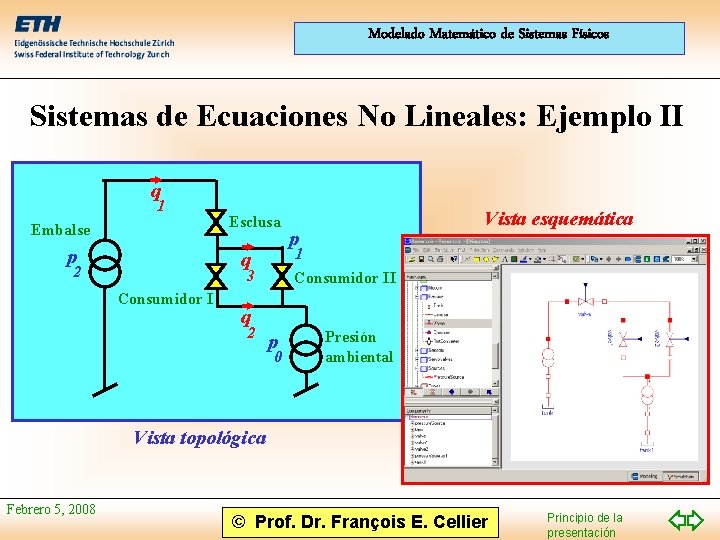
Modelado Matemático de Sistemas Físicos Sistemas de Ecuaciones No Lineales: Ejemplo II q 1 Embalse p Esclusa 3 Consumidor I p 1 q 2 Vista esquemática Consumidor II q 2 p 0 Presión ambiental Vista topológica Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

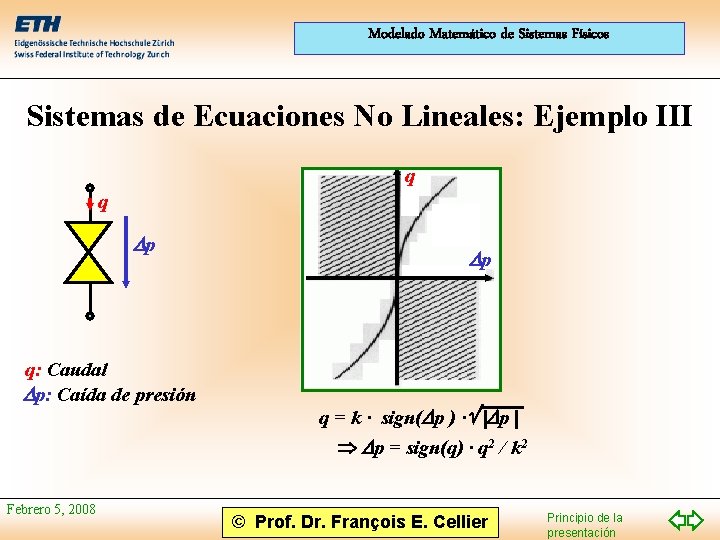
Modelado Matemático de Sistemas Físicos Sistemas de Ecuaciones No Lineales: Ejemplo III q q p q: Caudal p: Caída de presión Febrero 5, 2008 p q = k · sign( p ) · p p = sign(q) · q 2 / k 2 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Sistemas de Ecuaciones No Lineales: Ejemplo IV q 1 Embalse p Esclusa 1 q 2 3 Consumidor II q 2 p 0 Febrero 5, 2008 p Presión ambiental p 2 = 100 p 0 = 1 f. S(q 1 , p 2) = 0 f. I(q 2 , p 0 , p 1) = 0 f. II(q 3 , p 0 , p 1) = 0 q 1 = q 2 + q 3 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Sistemas de Ecuaciones No Lineales: Ejemplo V p 2 = 100 p 0 = 1 f. S (q 1 , p 2 ) = 0 f. I (q 2 , p 0 , p 1 ) = 0 f. II (q 3 , p 0 , p 1 ) = 0 q 1 - q 2 - q 3 = 0 Sistema de ecuaciones no lineales con 4 incógnitas Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton I x n f n Sistema de ecuaciones no lineales: f(x) = 0 Vector inicial: x 0 Fórmula de iteración: x i+1 = x i - x i x n Incremento: x i = H(x i )-1 · f(x i ) H n n Matriz Hessiana: f(x) H(x) = x Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton: Ejemplo I x= p 1 q 2 q 3 f(x) = H(x) = Febrero 5, 2008 p 2 - p 1 - sign(q 1) · q 12 /k 12 p 1 – p 0 - sign(q 2) · q 22 /k 22 =0 p 1 – p 0 - sign(q 3) · q 32 /k 32 q 1 - q 2 - q 3 -1 -2|q 1 |/k 12 0 0 1 0 -2|q 2 |/k 22 0 0 -2|q 3 |/k 32 1 0 -1 -1 0 1 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton II Cálculo del incremento: x i = H(x i )-1 · f(x i ) H(x i ) · x i = f(x i ) Sistema lineal de ecuaciones con incógnitas x Febrero 5, 2008 x n © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton con Rasgadura I p 2 = 100 p 0 = 1 f. S (q 1 , p 2 ) = 0 f. I (q 2 , p 0 , p 1 ) = 0 f. II (q 3 , p 0 , p 1 ) = 0 q 1 - q 2 - q 3 = 0 p 2 = 100 p 0 = 1 f. S (q 1 , p 2 ) = 0 f. I (q 2 , p 0 , p 1 ) = 0 f. II (q 3 , p 0 , p 1 ) = 0 q 1 - q 2 - q 3 = 0 Elección Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton con Rasgadura II p 2 = 100 p 0 = 1 f. S (q 1 , p 2 ) = 0 f. I (q 2 , p 0 , p 1 ) = 0 f. II (q 3 , p 0 , p 1 ) = 0 q 1 - q 2 - q 3 = 0 p 2 = 100 p 0 = 1 q 1 = q 2 + q 3 p 1 = f 1 (q 1 , p 2 ) q 2 = f 2 (p 0 , p 1 ) q 3 = f 3 (p 0 , p 1 ) q 1 = f 2 (p 0 , p 1 ) + f 3 (p 0 , p 1 ) = f 2 (p 0 , f 1 (q 1 , p 2 ) ) + f 3 (p 0 , f 1 (q 1 , p 2 )) Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton con Rasgadura III q 1 = f 2 (p 0 , p 1 ) + f 3 (p 0 , p 1 ) = f 2 (p 0 , f 1 (q 1 , p 2 ) ) + f 3 (p 0 , f 1 (q 1 , p 2 )) x = q 1 f(x) = q 1 - f 2 (p 0 , f 1 (q 1 , p 2 ) ) - f 3 (p 0 , f 1 (q 1 , p 2 )) = 0 H(x i ) · x i = f(x i ) Febrero 5, 2008 Sistema lineal de ecuaciones con incógnita x x 1 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton : Ejemplo II p 2 = 100 p 0 = 1 q 1 = q 2 + q 3 p 1 = p 2 - sign(q 1 ) · q 12 / k 12 q 2 = k 2 · sign(p 1 - p 0 ) · p 1 - p 0 q 3 = k 3 · sign(p 1 - p 0 ) · p 1 - p 0 pq 1 q 1 = 1 pp 1 q 1 = - 2|q 1| / k 12 pq 2 q 1 = k 2 / ( 2 · p 1 - p 0 ) · pp 1 q 1 pq 3 q 1 = k 3 / ( 2 · p 1 - p 0 ) · pp 1 q 1 f = q 1 - q 2 - q 3 h = pq 1 q 1 - pq 2 q 1 - pq 3 q 1 Febrero 5, 2008 La sustitución simbólica de expresiones casi nunca es provechosa. Es mucho mejor iterar sobre todas las ecuaciones y derivar cada ecuación en forma separada para determinar las derivadas parciales. © Prof. Dr. François E. Cellier Principio de la presentación

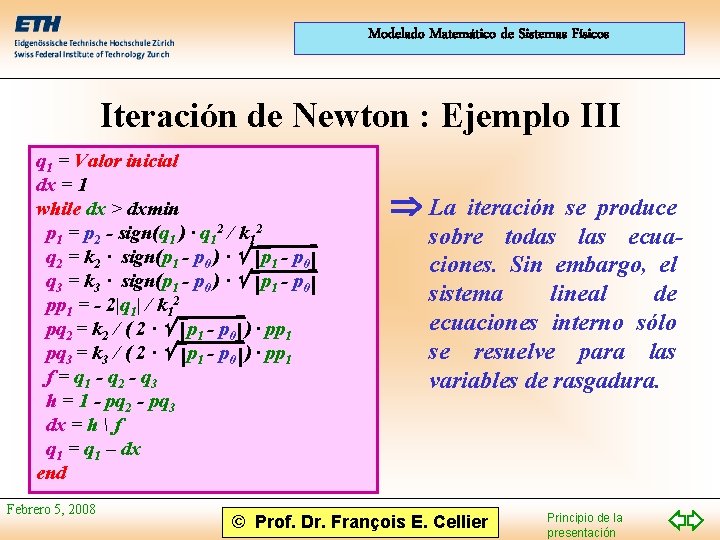
Modelado Matemático de Sistemas Físicos Iteración de Newton : Ejemplo III q 1 = Valor inicial dx = 1 while dx > dxmin p 1 = p 2 - sign(q 1 ) · q 12 / k 12 q 2 = k 2 · sign(p 1 - p 0 ) · p 1 - p 0 q 3 = k 3 · sign(p 1 - p 0 ) · p 1 - p 0 pp 1 = - 2|q 1| / k 12 pq 2 = k 2 / ( 2 · p 1 - p 0 ) · pp 1 pq 3 = k 3 / ( 2 · p 1 - p 0 ) · pp 1 f = q 1 - q 2 - q 3 h = 1 - pq 2 - pq 3 dx = h f q 1 = q 1 – dx end Febrero 5, 2008 La iteración se produce sobre todas las ecuaciones. Sin embargo, el sistema lineal de ecuaciones interno sólo se resuelve para las variables de rasgadura. © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Iteración de Newton en Sistemas Lineales Sistema lineal: A·x = b f(x) = A·x – b = 0 H(x) = f(x)/ x = A A· x = A·x – b x = x – A-1·b x 1 = x 0 – (x 0 – A-1·b) = A-1·b Febrero 5, 2008 La iteración de Newton converge tras una sola iteración. © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Conclusiones • El método de rasgadura es igualmente apto para el uso con sistemas lineales y no lineales. • La iteración de Newton en un sistema de ecuaciones no lineales conduce internamente a la resolución de un sistema de ecuaciones lineales. La matriz Hessiana de este sistema de ecuaciones lineales sólo necesita ser determinada para las variables de rasgadura. • La iteración de Newton puede también utilizarse muy eficientemente para la resolución de sistemas lineales en muchas variables ya que converge en un sólo paso (con el cálculo correcto de la matriz H(x)). • En la práctica, la matriz H(x) generalmente se aproxima de manera numérica en lugar de calcularse analíticamente. • De todas maneras, las técnicas de manipulación simbólica de fórmulas pueden usarse para obtener expresiones simbólicas de los elementos de la matriz Hessiana. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación