Modelado Matemtico de Sistemas Fsicos El Algoritmo de

Modelado Matemático de Sistemas Físicos El Algoritmo de Tarjan para la Ordenación de Ecuaciones • En esa presentación introducimos un algoritmo de ordenación de ecuaciones que encuentra bucles algebraicos de tamaño mínimo y los aísla de forma sistemática y algorítmica. • El algoritmo de Tarjan consiste es un algoritmo gráfico que simultáneamente ordena sistemas grandes de ecuaciones horizontalmente y verticalmente. El algoritmo además detecta bucles algebraicos de tamaño mínimo. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Contenido • • La matriz de incidencia estructural El dígrafo de la estructura El algoritmo de Tarjan La rasgadura de sistemas algebraicos de ecuaciones Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos La Matriz de Incidencia Estructural I • La matriz de incidencia estructural contiene una fila para cada ecuación del sistema EDA y una columna para cada incógnita del sistema de ecuaciones. • Ya que un sistema completo de ecuaciones siempre contiene el mismo número de ecuaciones que de incógnitas, la matriz de incidencia estructural es cuadrada. • El elemento <i, j> de la matriz de incidencia estructural trata con la ecuación i y con la incógnita j. El elemento recibe un valor de 1 si la variable indicada aparece en la ecuación considerada. Si no es el caso, el elemento <i, j> recibe un valor de 0. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos La Matriz de Incidencia Estructural: Un Ejemplo 1: U 0 = f(t) 2: i 0 = i. L + i. R 1 3: u. L = U 0 4: di. L/dt = u. L / L 1 5: v 1 = U 0 6: u. R 1 = v 1 – v 2 7: i. R 1 = u. R 1 / R 1 8: v 2 = u. C 9: i. C = i. R 1 – i. R 2 10: du. C/dt = i. C / C 1 11: u. R 2 = u. C 12: i. R 2 = u. R 2 / R 2 Febrero 5, 2008 U 0 S= 01 02 03 04 05 06 07 08 09 10 11 12 1 0 1 0 0 0 0 i 0 u. L 0 1 0 0 0 1 1 0 0 0 0 di. L v u i 1 R 1 v 2 dt 0 0 0 1 0 0 0 1 1 0 0 0 © Prof. Dr. François E. Cellier 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 i. C du. C u. R 2 i. R 2 dt 0 0 0 0 1 1 0 0 0 0 0 0 1 1 Principio de la presentación 0 0 0 0 1

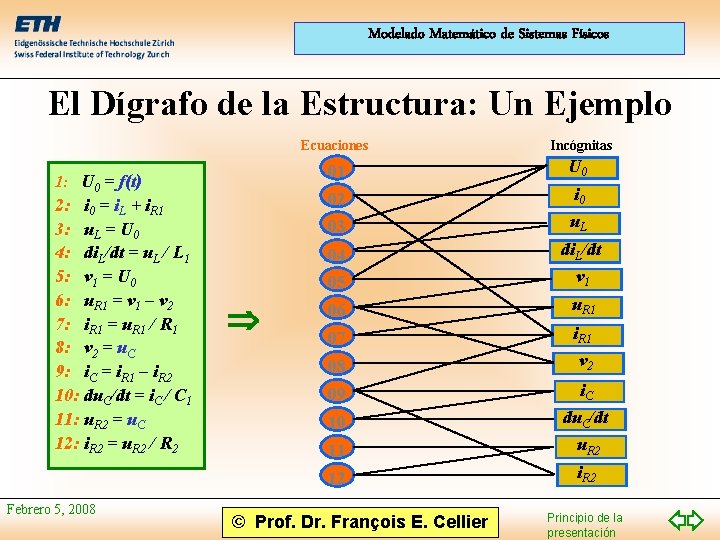
Modelado Matemático de Sistemas Físicos El Dígrafo de la Estructura • El dígrafo de la estructura contiene la misma información que la matriz de incidencia estructural. La información es representada de forma diferente. • El dígrafo de la estructura enumera las ecuaciones a la izquierda y las incógnitas a la derecha. Una conexión entre una ecuación y una incógnita indica que la incógnita aparece en la ecuación. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Dígrafo de la Estructura: Un Ejemplo 1: U 0 = f(t) 2: i 0 = i. L + i. R 1 3: u. L = U 0 4: di. L/dt = u. L / L 1 5: v 1 = U 0 6: u. R 1 = v 1 – v 2 7: i. R 1 = u. R 1 / R 1 8: v 2 = u. C 9: i. C = i. R 1 – i. R 2 10: du. C/dt = i. C / C 1 11: u. R 2 = u. C 12: i. R 2 = u. R 2 / R 2 Febrero 5, 2008 Ecuaciones Incógnitas 01 U 0 02 i 0 03 u. L 04 05 di. L/dt v 1 06 u. R 1 07 i. R 1 08 v 2 09 i. C 10 du. C/dt 11 u. R 2 12 i. R 2 © Prof. Dr. François E. Cellier Principio de la presentación

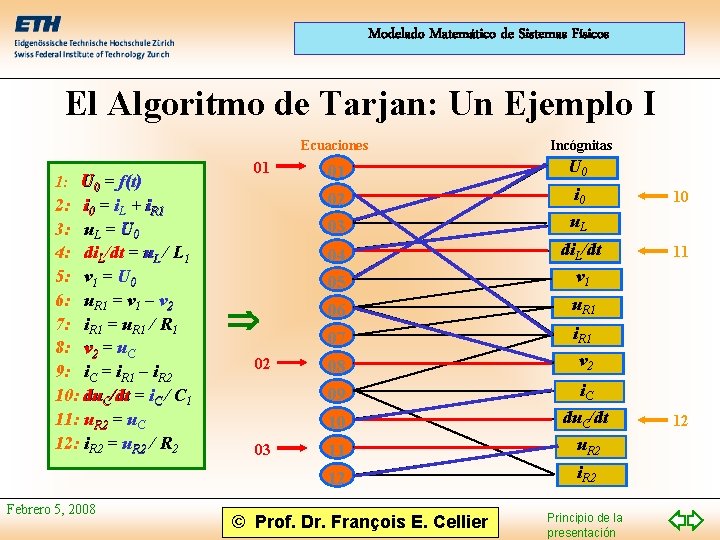
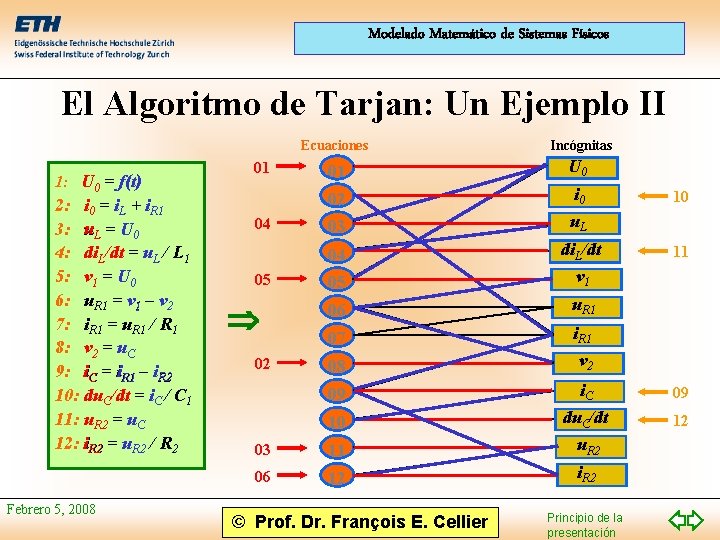
Modelado Matemático de Sistemas Físicos El Algoritmo de Tarjan • El algoritmo de Tarjan es basado en el dígrafo estructural. • Se trata de un algoritmo de coloración del dígrafo. Si una ecuación tiene solamente una conexión negra, esta conexión se colorea en rojo; la ecuación se enumera de nuevo empezando con 1; y todas las conexiones negras que terminan en la misma variable se colorean en azul. Si una variable tiene solamente una conexión negra, esta conexión se colorea en rojo; la ecuación se enumera de nuevo empezando con n; y todas las conexiones negras que comienzan en la misma ecuación se colorean en azul. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos El Algoritmo de Tarjan: Un Ejemplo I 1: U 0 = f(t) 2: i 0 = i. L + i. R 1 3: u. L = U 0 4: di. L/dt = u. L / L 1 5: v 1 = U 0 6: u. R 1 = v 1 – v 2 7: i. R 1 = u. R 1 / R 1 8: v 2 = u. C 9: i. C = i. R 1 – i. R 2 10: du. C/dt = i. C / C 1 11: u. R 2 = u. C 12: i. R 2 = u. R 2 / R 2 Febrero 5, 2008 01 02 03 Ecuaciones Incógnitas 01 U 0 02 i 0 03 u. L 04 05 di. L/dt v 1 06 u. R 1 07 i. R 1 08 v 2 09 i. C 10 du. C/dt 11 u. R 2 12 i. R 2 © Prof. Dr. François E. Cellier Principio de la presentación 10 11 12

Modelado Matemático de Sistemas Físicos El Algoritmo de Tarjan: Un Ejemplo II 1: U 0 = f(t) 2: i 0 = i. L + i. R 1 3: u. L = U 0 4: di. L/dt = u. L / L 1 5: v 1 = U 0 6: u. R 1 = v 1 – v 2 7: i. R 1 = u. R 1 / R 1 8: v 2 = u. C 9: i. C = i. R 1 – i. R 2 10: du. C/dt = i. C / C 1 11: u. R 2 = u. C 12: i. R 2 = u. R 2 / R 2 Febrero 5, 2008 Ecuaciones Incógnitas 01 U 0 02 i 0 03 u. L 04 05 di. L/dt v 1 06 u. R 1 07 i. R 1 08 v 2 09 i. C 09 10 du. C/dt 12 03 11 u. R 2 06 12 i. R 2 01 04 05 02 © Prof. Dr. François E. Cellier Principio de la presentación 10 11

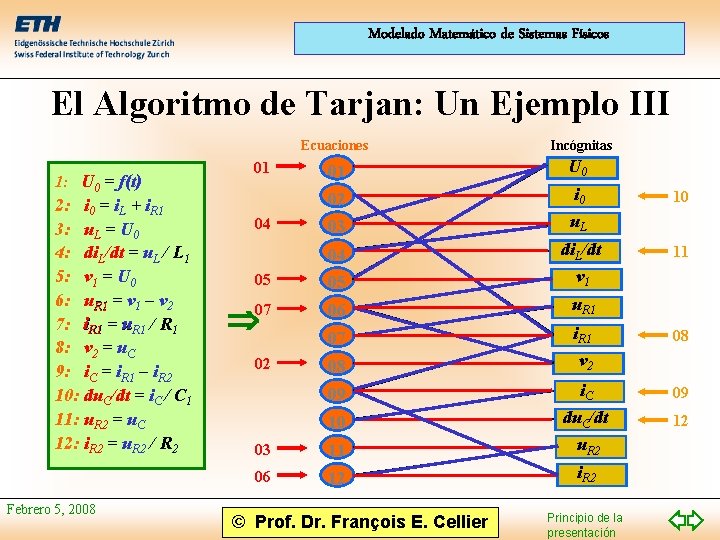
Modelado Matemático de Sistemas Físicos El Algoritmo de Tarjan: Un Ejemplo III 1: U 0 = f(t) 2: i 0 = i. L + i. R 1 3: u. L = U 0 4: di. L/dt = u. L / L 1 5: v 1 = U 0 6: u. R 1 = v 1 – v 2 7: i. R 1 = u. R 1 / R 1 8: v 2 = u. C 9: i. C = i. R 1 – i. R 2 10: du. C/dt = i. C / C 1 11: u. R 2 = u. C 12: i. R 2 = u. R 2 / R 2 Febrero 5, 2008 Ecuaciones Incógnitas 01 U 0 02 i 0 03 u. L 04 05 di. L/dt v 1 06 u. R 1 07 i. R 1 08 v 2 09 i. C 09 10 du. C/dt 12 03 11 u. R 2 06 12 i. R 2 01 04 05 07 02 © Prof. Dr. François E. Cellier Principio de la presentación 10 11 08

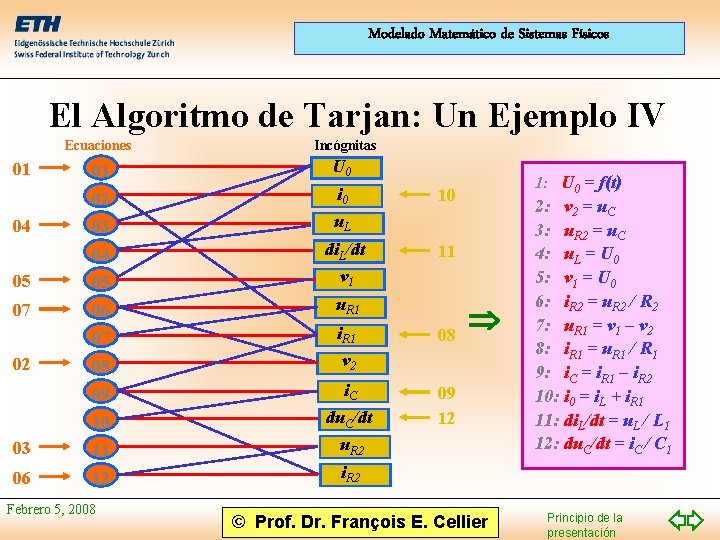
Modelado Matemático de Sistemas Físicos El Algoritmo de Tarjan: Un Ejemplo IV 01 04 Ecuaciones Incógnitas 01 U 0 02 i 0 03 u. L 04 05 05 di. L/dt v 1 07 06 u. R 1 07 i. R 1 08 v 2 09 i. C 10 du. C/dt 03 11 u. R 2 06 12 i. R 2 02 Febrero 5, 2008 1: U 0 = f(t) 10 11 08 09 12 © Prof. Dr. François E. Cellier 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C/dt = i. C / C 1 Principio de la presentación

Modelado Matemático de Sistemas Físicos La Matriz de Incidencia Estructural II 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C/dt = i. C / C 1 Febrero 5, 2008 U 0 v 2 u. R 2 u. L v 1 i. R 2 u. R 1 i. C S= 01 02 03 04 05 06 07 08 09 10 11 12 1 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 i 0 di. L du. C dt dt 0 0 0 0 0 1 0 0 La 0 0 0 0 0 1 0 0 0 1 matriz de incidencia estructural del sistema de ecuaciones completamente ordenadas es triangular inferior. © Prof. Dr. François E. Cellier Principio de la presentación

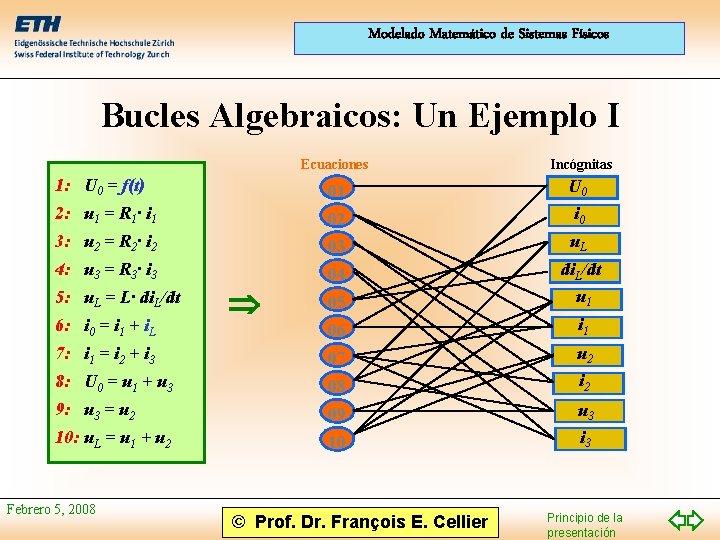
Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo I Ecuaciones Incógnitas 1: U 0 = f(t) 01 U 0 2: u 1 = R 1· i 1 02 i 0 3: u 2 = R 2· i 2 03 u. L 4: u 3 = R 3· i 3 04 05 di. L/dt u 1 06 i 1 7: i 1 = i 2 + i 3 07 u 2 8: U 0 = u 1 + u 3 08 i 2 9: u 3 = u 2 09 u 3 10: u. L = u 1 + u 2 10 i 3 5: u. L = L· di. L/dt 6: i 0 = i 1 + i. L Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

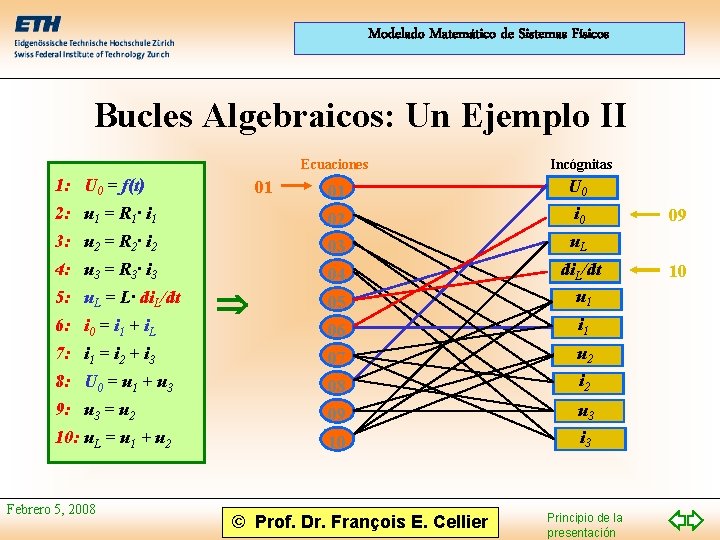
Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo II Ecuaciones Incógnitas 01 U 0 2: u 1 = R 1· i 1 02 i 0 3: u 2 = R 2· i 2 03 u. L 4: u 3 = R 3· i 3 04 05 di. L/dt u 1 06 i 1 7: i 1 = i 2 + i 3 07 u 2 8: U 0 = u 1 + u 3 08 i 2 9: u 3 = u 2 09 u 3 10: u. L = u 1 + u 2 10 i 3 1: U 0 = f(t) 5: u. L = L· di. L/dt 6: i 0 = i 1 + i. L Febrero 5, 2008 01 © Prof. Dr. François E. Cellier Principio de la presentación 09 10

Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo III 01 1: U 0 = f(t) 2: u 1 = R 1· i 1 3: u 2 = R 2· i 2 4: u 3 = R 3· i 3 5: u. L = L· di. L/dt 6: i 0 = i 1 + i. L 7: i 1 = i 2 + i 3 8: U 0 = u 1 + u 3 9: u 3 = u 2 10: u. L = u 1 + u 2 Febrero 5, 2008 Ecuaciones Incógnitas 01 U 0 02 i 0 09 03 u. L 04 05 di. L/dt u 1 08 10 06 i 1 07 u 2 08 i 2 09 u 3 10 i 3 El algoritmo se atasca porque no se encuentran más ni ecuaciones ni variables con una sola conexión negra. © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos La Rasgadura de Bucles Algebraicos I • La heurística siguiente puede usarse para encontrar variables de rasgadura adecuadas: A cada conexión negra dale como peso el número de conexiones negras de su ecuación más el número de conexiones negras de su variable. Para cada conexión negra con peso máximo, colorea esa conexión temporalmente en rojo y todas las demás conexiones negras de su ecuación y de su variable en azul. Calcula cuantas ecuaciones adicionales pueden hacerse causal de esa manera y selecciona permanentemente la conexión con peso máximo que permite hacer causal el más grande número de ecuaciones adicionales. Su ecuación se llama ecuación residual y su variable se llama variable de rasgadura. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

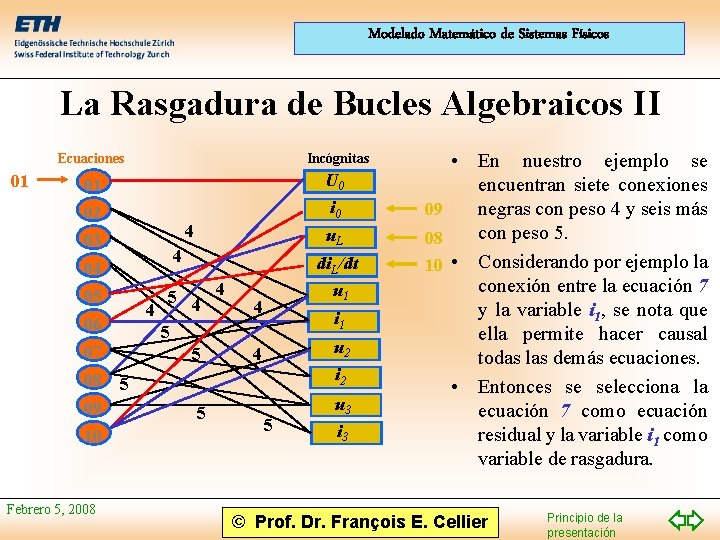
Modelado Matemático de Sistemas Físicos La Rasgadura de Bucles Algebraicos II 01 Ecuaciones Incógnitas 01 U 0 02 i 0 03 04 05 06 07 08 5 09 10 Febrero 5, 2008 4 u. L 4 5 4 4 4 5 5 di. L/dt u 1 4 i 1 u 2 4 i 2 5 5 u 3 i 3 • En nuestro ejemplo se encuentran siete conexiones negras con peso 4 y seis más 09 con peso 5. 08 10 • Considerando por ejemplo la conexión entre la ecuación 7 y la variable i 1, se nota que ella permite hacer causal todas las demás ecuaciones. • Entonces se selecciona la ecuación 7 como ecuación residual y la variable i 1 como variable de rasgadura. © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo IV Ecuaciones Incógnitas 01 U 0 2: u 1 = R 1· i 1 02 i 0 09 3: u 2 = R 2· i 2 03 u. L 4: u 3 = R 3· i 3 04 05 di. L/dt u 1 08 10 06 i 1 07 u 2 8: U 0 = u 1 + u 3 08 i 2 9: u 3 = u 2 09 u 3 10: u. L = u 1 + u 2 10 i 3 1: U 0 = f(t) 5: u. L = L· di. L/dt 6: i 0 = i 1 + i. L 7: i 1 = i 2 + i 3 01 02 Selección Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

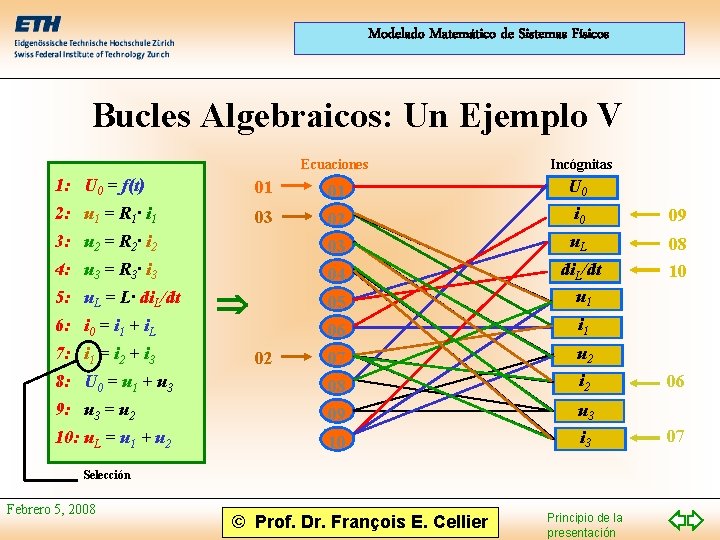
Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo V Ecuaciones Incógnitas 1: U 0 = f(t) 01 01 U 0 2: u 1 = R 1· i 1 03 02 i 0 09 3: u 2 = R 2· i 2 03 u. L 4: u 3 = R 3· i 3 04 05 di. L/dt u 1 08 10 06 i 1 07 u 2 8: U 0 = u 1 + u 3 08 i 2 9: u 3 = u 2 09 u 3 10: u. L = u 1 + u 2 10 i 3 5: u. L = L· di. L/dt 6: i 0 = i 1 + i. L 7: i 1 = i 2 + i 3 02 Selección Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación 06 07

Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo VI Ecuaciones Incógnitas 1: U 0 = f(t) 01 01 U 0 2: u 1 = R 1· i 1 03 02 i 0 09 3: u 2 = R 2· i 2 03 u. L 4: u 3 = R 3· i 3 04 05 di. L/dt u 1 08 10 06 i 1 07 u 2 05 08 i 2 06 9: u 3 = u 2 09 u 3 10: u. L = u 1 + u 2 10 i 3 5: u. L = L· di. L/dt 6: i 0 = i 1 + i. L 7: i 1 = i 2 + i 3 8: U 0 = u 1 + u 3 02 04 Selección Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación 07

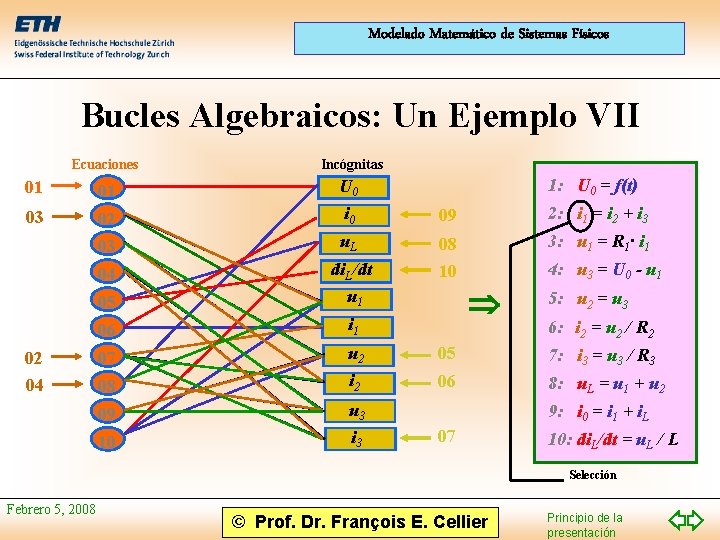
Modelado Matemático de Sistemas Físicos Bucles Algebraicos: Un Ejemplo VII Ecuaciones Incógnitas 01 01 U 0 03 02 i 0 09 2: i 1 = i 2 + i 3 03 u. L 3: u 1 = R 1· i 1 04 05 di. L/dt u 1 08 10 06 i 1 07 u 2 05 7: i 3 = u 3 / R 3 08 i 2 06 8: u. L = u 1 + u 2 09 u 3 10 i 3 02 04 1: U 0 = f(t) 4: u 3 = U 0 - u 1 5: u 2 = u 3 6: i 2 = u 2 / R 2 9: i 0 = i 1 + i. L 07 10: di. L/dt = u. L / L Selección Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

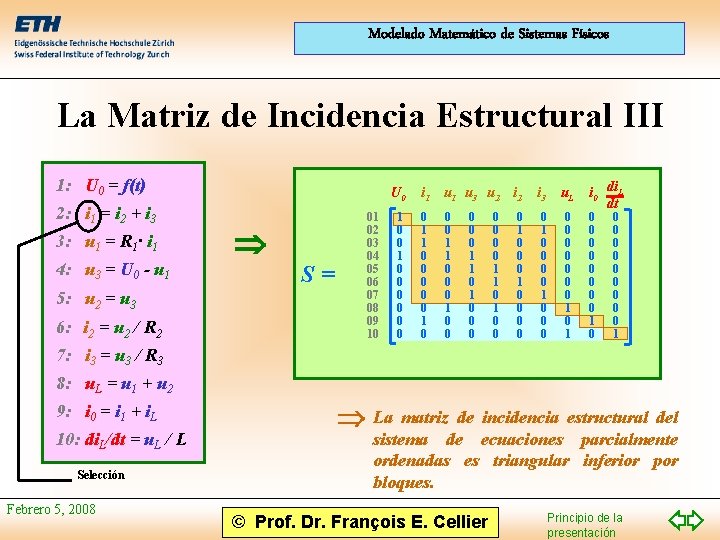
Modelado Matemático de Sistemas Físicos La Matriz de Incidencia Estructural III 1: U 0 = f(t) 2: i 1 = i 2 + i 3 3: u 1 = R 1· i 1 4: u 3 = U 0 - u 1 5: u 2 = u 3 6: i 2 = u 2 / R 2 U 0 S= 01 02 03 04 05 06 07 08 09 10 1 0 0 0 0 i 1 u 3 ui 32 i 2 0 1 1 0 0 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 i 3 u. L 0 1 0 0 0 0 1 i 0 di. L dt 0 0 0 0 1 0 0 0 0 0 1 7: i 3 = u 3 / R 3 8: u. L = u 1 + u 2 9: i 0 = i 1 + i. L 10: di. L/dt = u. L / L Selección Febrero 5, 2008 La matriz de incidencia estructural del sistema de ecuaciones parcialmente ordenadas es triangular inferior por bloques. © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos La Solución de Bucles Algebraicos I • El algoritmo de Tarjan identifica y aísla bucles algebraicos. • El algoritmo transforma la matriz de incidencia estructural a la forma TIB (triangular inferior por bloques). Los bloques en la diagonal se quedan de tamaño mínimo. • Las variables de rasgadura no se seleccionan de una forma verdaderamente óptima. Eso no sería razonable porque puede enseñarse que la selección óptima de las variables de rasgadura requiere un algoritmo np-completo. En su lugar se propuso un algoritmo heurístico que normalmente resulta en un número pequeño de variables de rasgadura aunque no necesariamente en el número mínimo. • El algoritmo de Tarjan no trata con la cuestión de como los bucles algebraicos estén resueltos. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos La Solución de Bucles Algebraicos II • Los bucles algebraicos pueden resolverse usando métodos analíticos o numéricos. • Si las ecuaciones del bucle son no lineales una iteración de Newton sobre las variables de rasgadura es normalmente óptima. • Si las ecuaciones del bucle son lineales y si se trata de un bucle relativamente grande (más de 5 ecuaciones y variables), la iteración de Newton es aún la solución óptima. • Si las ecuaciones del bucle son lineales y si se trata de un bucle relativamente pequeño, las ecuaciones pueden resolverse o por técnicas de matrices o por manipulación de formulas. • El entorno de modelado de Modelica usa heurísticas para elegir automáticamente la técnica más adecuada en cada caso. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Referencias • Elmqvist H. and M. Otter (1994), “Methods for tearing systems of equations in object-oriented modeling, ” Proc. European Simulation Multiconference, Barcelona, Spain, pp. 326 -332. • Tarjan R. E. (1972), “Depth first search and linear graph algorithms, ” SIAM J. Comp. , 1, pp. 146 -160. Febrero 5, 2008 © Prof. Dr. François E. Cellier Principio de la presentación