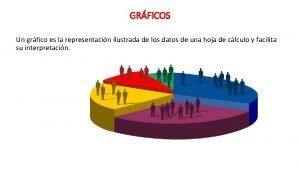
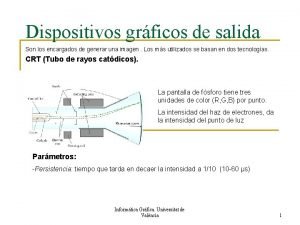
Modelado Matemtico de Sistemas Fsicos Grficos de Ligaduras

Modelado Matemático de Sistemas Físicos Gráficos de Ligaduras de Sistemas Mecánicos • Veremos ahora con algo más de detalle el modelado de sistemas mecánicos 1 D utilizando gráficos de ligaduras. • En primer lugar, veremos el problema de las restricciones holonómicas en sistemas mecánicos. • Luego, discutiremos como puede construirse una librería de gráficos de ligaduras envasados de sistemas mecánicos. • Finalmente, veremos un algoritmo simbólico para la selección de estados. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Contenido • Variables de estado en sistemas mecánicos • Restricciones holonómicas • Envase de gráficos de ligaduras de sistemas mecánicos • Selección de estados • Condiciones iniciales • Variables protegidas • Ejemplo • Algoritmo de selección de estados Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Variables de Estado en Sistemas Mecánicos • Ya hemos visto que las masas (inercias) pueden modelarse usando inductores de gráficos de ligaduras, mientras que los muelles pueden modelarse utilizando capacidades. Luego, las variables de estado naturales para una descripción en gráficos de ligaduras de sistemas mecánicos son las velocidades (angulares) absolutas de los cuerpos y las fuerzas (pares de torsión) en los muelles. • En el modelo de un sistema mecánico descrito de esta manera, las posiciones (angulares) se pierden. Éstas no son necesarias para una descripción propia y completa de la dinámica del sistema. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Restricciones Holonómicas I • Esto causa problemas, ya que es relevante saber si dos cuerpos ocupan el mismo lugar en el mismo instante, es decir, si los cuerpos chocan entre sí. • También, cuando dos cuerpos están conectados en un punto (por ejemplo a través de una articulación), no alcanza con decir que las velocidades de estos puntos son iguales. Debe decirse que las posiciones son idénticas. • Tales restricciones posicionales, en la literatura de la mecánica, se denominan restricciones holonómicas. • Las restricciones correspondientes en la velocidad (restricciones no holonómicas) no necesitan especificarse por separado ya que pueden derivarse automáticamente de las restricciones holonómicas. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Restricciones Holonómicas II • Por esto, convendría encontrar una descripción alternativa que utilice velocidades y posiciones absolutas de los cuerpos como variables de estado, dejando de lado las fuerzas en los muelles. • ¿Puede hacerse esto en el marco de la metodología de los gráficos de ligaduras? • Sí, y así es como se construyeron las dos librerías de gráficos de ligaduras envasados de mecánica 1 D (para movimientos de traslado y de giro). Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

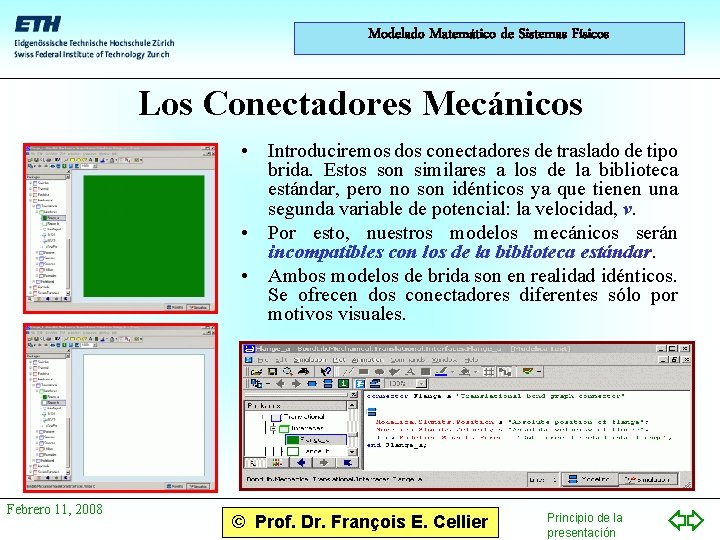
Modelado Matemático de Sistemas Físicos Los Conectadores Mecánicos • Introduciremos dos conectadores de traslado de tipo brida. Estos son similares a los de la biblioteca estándar, pero no son idénticos ya que tienen una segunda variable de potencial: la velocidad, v. • Por esto, nuestros modelos mecánicos serán incompatibles con los de la biblioteca estándar. • Ambos modelos de brida son en realidad idénticos. Se ofrecen dos conectadores diferentes sólo por motivos visuales. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

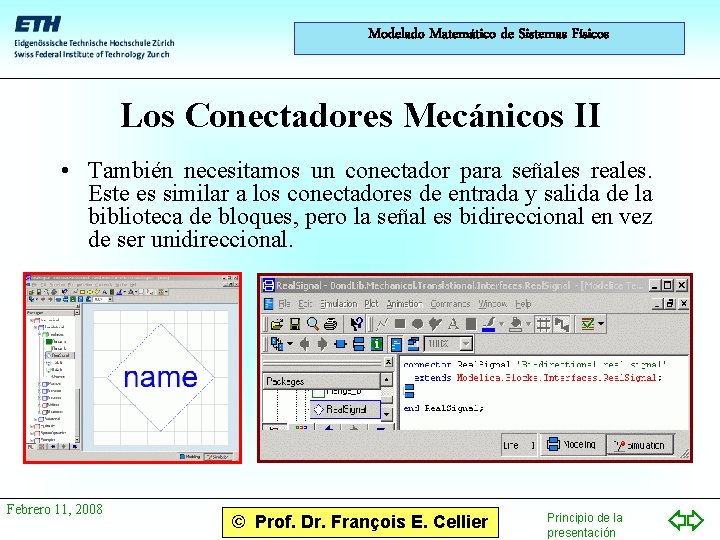
Modelado Matemático de Sistemas Físicos Los Conectadores Mecánicos II • También necesitamos un conectador para señales reales. Este es similar a los conectadores de entrada y salida de la biblioteca de bloques, pero la señal es bidireccional en vez de ser unidireccional. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

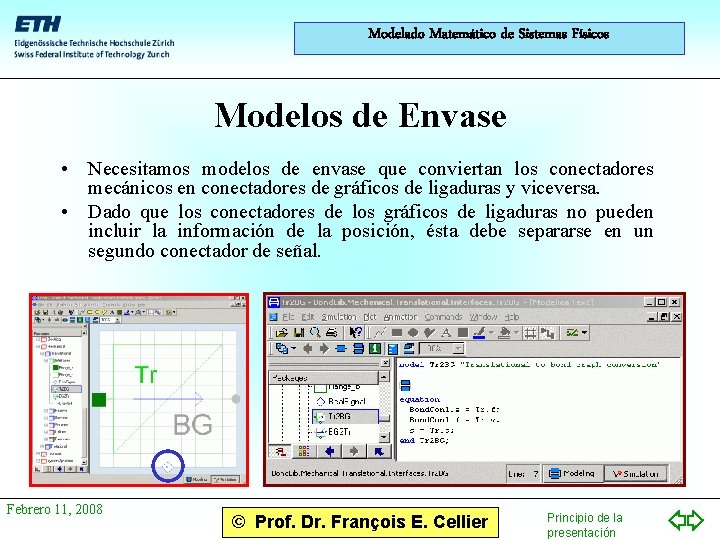
Modelado Matemático de Sistemas Físicos Modelos de Envase • Necesitamos modelos de envase que conviertan los conectadores mecánicos en conectadores de gráficos de ligaduras y viceversa. • Dado que los conectadores de los gráficos de ligaduras no pueden incluir la información de la posición, ésta debe separarse en un segundo conectador de señal. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

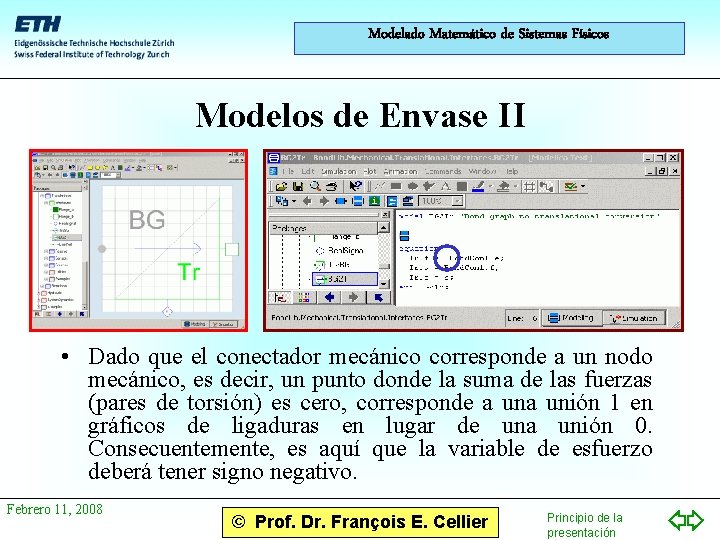
Modelado Matemático de Sistemas Físicos Modelos de Envase II • Dado que el conectador mecánico corresponde a un nodo mecánico, es decir, un punto donde la suma de las fuerzas (pares de torsión) es cero, corresponde a unión 1 en gráficos de ligaduras en lugar de una unión 0. Consecuentemente, es aquí que la variable de esfuerzo deberá tener signo negativo. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

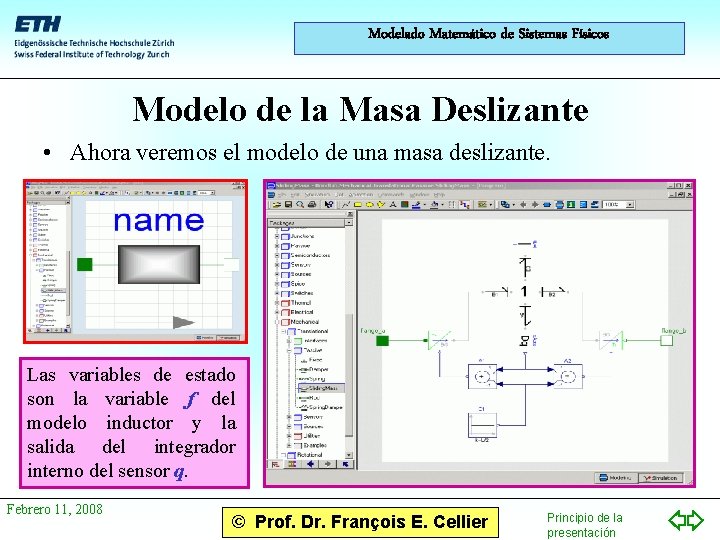
Modelado Matemático de Sistemas Físicos Modelo de la Masa Deslizante • Ahora veremos el modelo de una masa deslizante. Las variables de estado son la variable f del modelo inductor y la salida del integrador interno del sensor q. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

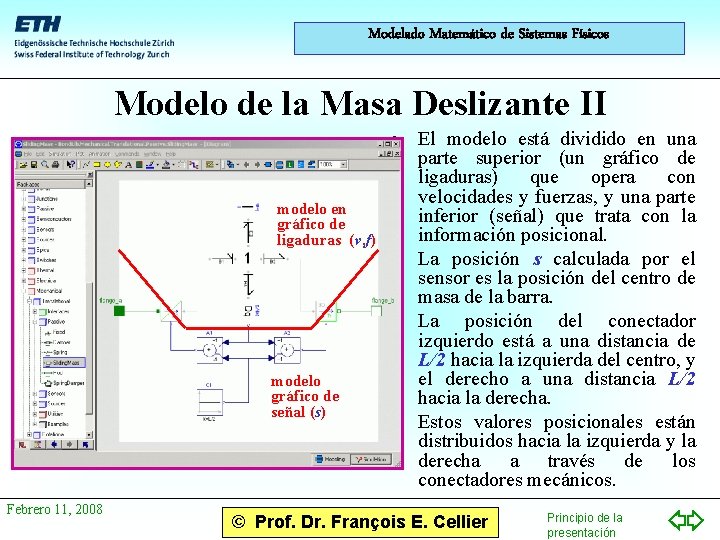
Modelado Matemático de Sistemas Físicos Modelo de la Masa Deslizante II modelo en gráfico de ligaduras (v, f) modelo gráfico de señal (s) Febrero 11, 2008 • El modelo está dividido en una parte superior (un gráfico de ligaduras) que opera con velocidades y fuerzas, y una parte inferior (señal) que trata con la información posicional. • La posición s calculada por el sensor es la posición del centro de masa de la barra. • La posición del conectador izquierdo está a una distancia de L/2 hacia la izquierda del centro, y el derecho a una distancia L/2 hacia la derecha. • Estos valores posicionales están distribuidos hacia la izquierda y la derecha a través de los conectadores mecánicos. © Prof. Dr. François E. Cellier Principio de la presentación

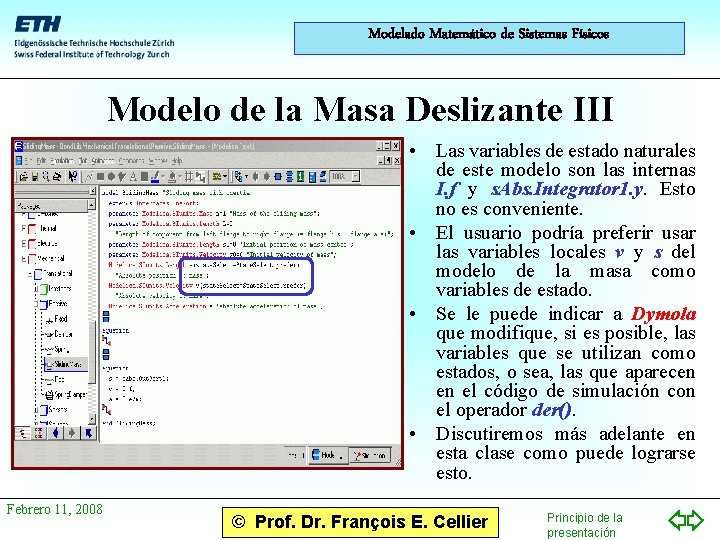
Modelado Matemático de Sistemas Físicos Modelo de la Masa Deslizante III • Las variables de estado naturales de este modelo son las internas I. f y s. Abs. Integrator 1. y. Esto no es conveniente. • El usuario podría preferir usar las variables locales v y s del modelo de la masa como variables de estado. • Se le puede indicar a Dymola que modifique, si es posible, las variables que se utilizan como estados, o sea, las que aparecen en el código de simulación con el operador der(). • Discutiremos más adelante en esta clase como puede lograrse esto. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

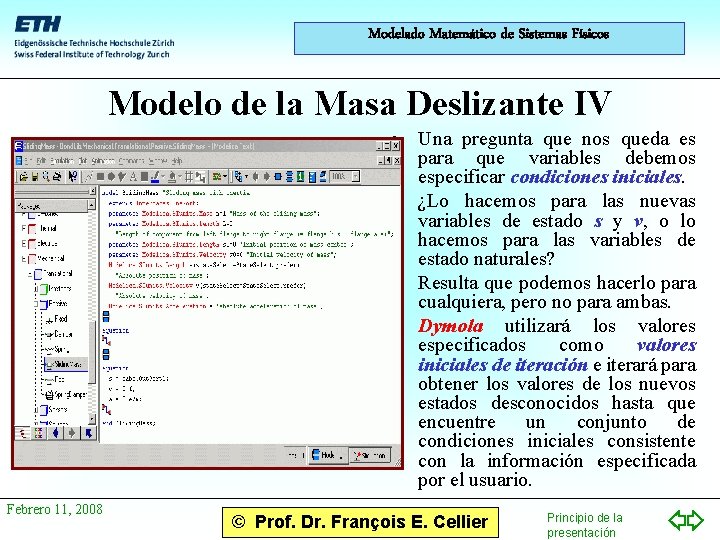
Modelado Matemático de Sistemas Físicos Modelo de la Masa Deslizante IV • Una pregunta que nos queda es para que variables debemos especificar condiciones iniciales. • ¿Lo hacemos para las nuevas variables de estado s y v, o lo hacemos para las variables de estado naturales? • Resulta que podemos hacerlo para cualquiera, pero no para ambas. • Dymola utilizará los valores especificados como valores iniciales de iteración e iterará para obtener los valores de los nuevos estados desconocidos hasta que encuentre un conjunto de condiciones iniciales consistente con la información especificada por el usuario. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

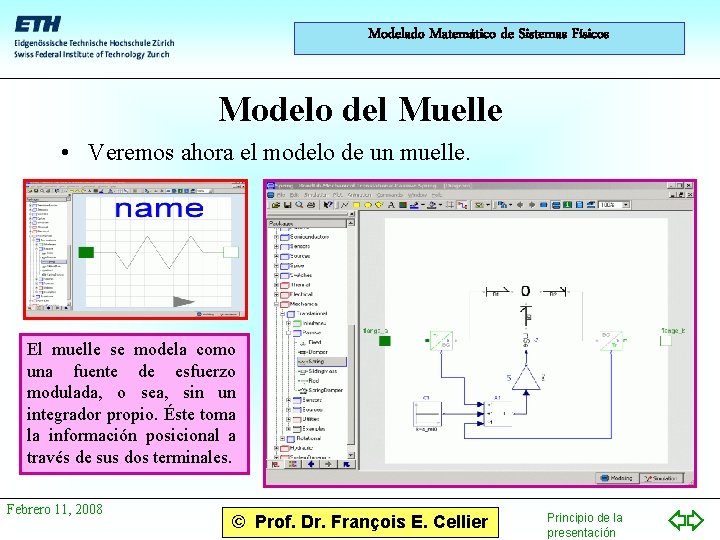
Modelado Matemático de Sistemas Físicos Modelo del Muelle • Veremos ahora el modelo de un muelle. El muelle se modela como una fuente de esfuerzo modulada, o sea, sin un integrador propio. Éste toma la información posicional a través de sus dos terminales. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

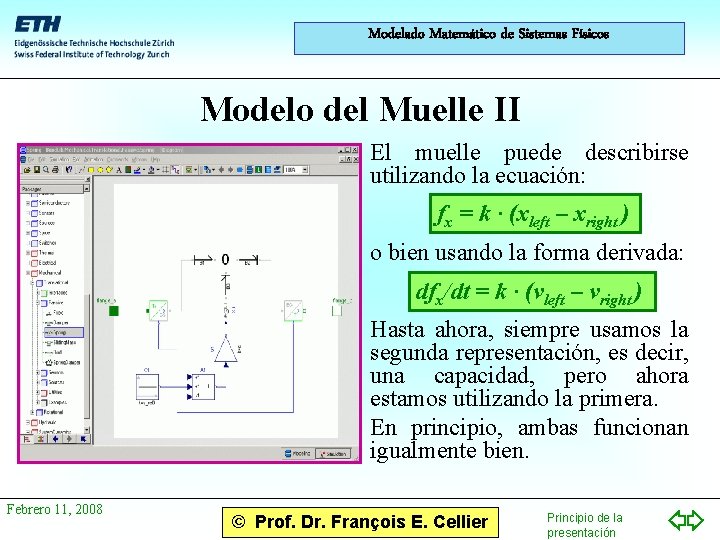
Modelado Matemático de Sistemas Físicos Modelo del Muelle II • El muelle puede describirse utilizando la ecuación: fx = k · (xleft – xright ) • o bien usando la forma derivada: dfx/dt = k · (vleft – vright ) • Hasta ahora, siempre usamos la segunda representación, es decir, una capacidad, pero ahora estamos utilizando la primera. • En principio, ambas funcionan igualmente bien. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Modelo del Muelle III • Hay un problema, sin embargo. • El nuevo modelo de muelle toma la información posicional necesaria a través de sus dos terminales. • Como la información posicional se calcula únicamente en las masas y marcos inerciales, este modelo puede ser colocado sólo entre dos masas o entre una masa y la tierra. • En particular, no es posible conectar en serie un muelle y un amortiguador. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Modelo del Muelle IV • El modelo anterior (con una capacidad) no tiene esta limitación. • Por esto, nuestro nuevo modelo de muelle explota un pequeño truco. • … el mismo truco que de hecho usa la biblioteca estándar, aunque sin ofrecer una interpretación en gráficos de ligaduras. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Modelo del Muelle V • La capa de las ecuaciones no ofrece ninguna sorpresa. • La posición y velocidad relativa del muelle se calculan aquí, ya que estas son variables que el usuario podría querer graficar. El resto de los modelos de la biblioteca son lo que esperaríamos que fueran, y por lo tanto no hace falta discutirlos aquí. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

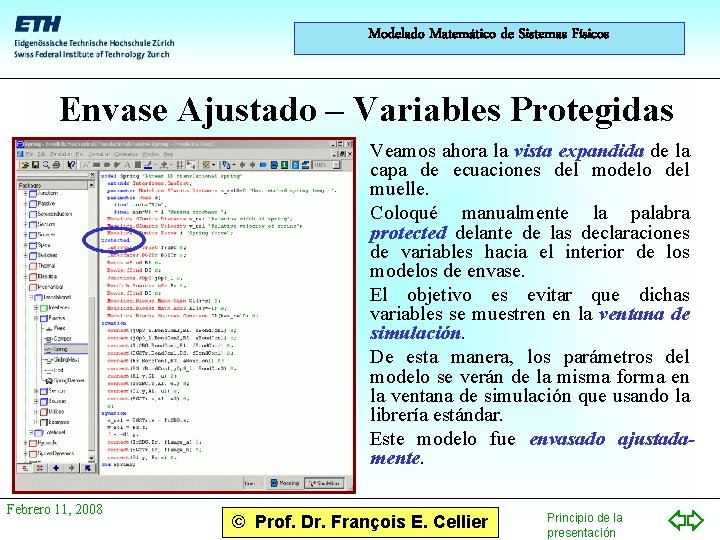
Modelado Matemático de Sistemas Físicos Envase Ajustado – Variables Protegidas • Veamos ahora la vista expandida de la capa de ecuaciones del modelo del muelle. • Coloqué manualmente la palabra protected delante de las declaraciones de variables hacia el interior de los modelos de envase. • El objetivo es evitar que dichas variables se muestren en la ventana de simulación. • De esta manera, los parámetros del modelo se verán de la misma forma en la ventana de simulación que usando la librería estándar. • Este modelo fue envasado ajustadamente. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

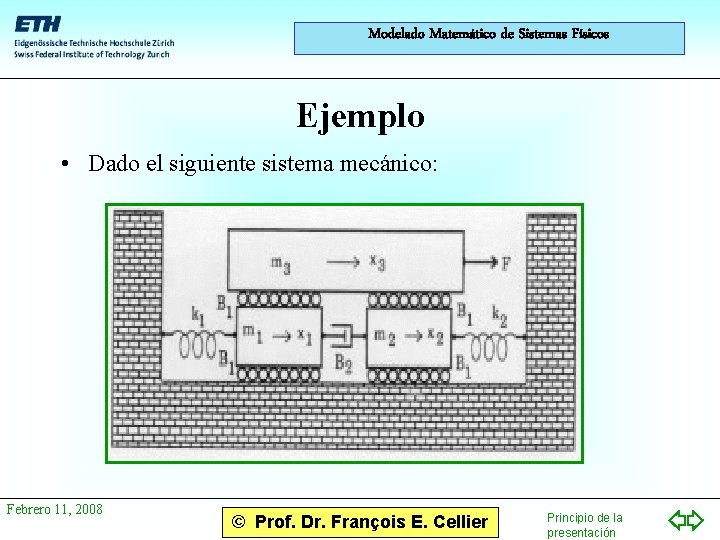
Modelado Matemático de Sistemas Físicos Ejemplo • Dado el siguiente sistema mecánico: Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

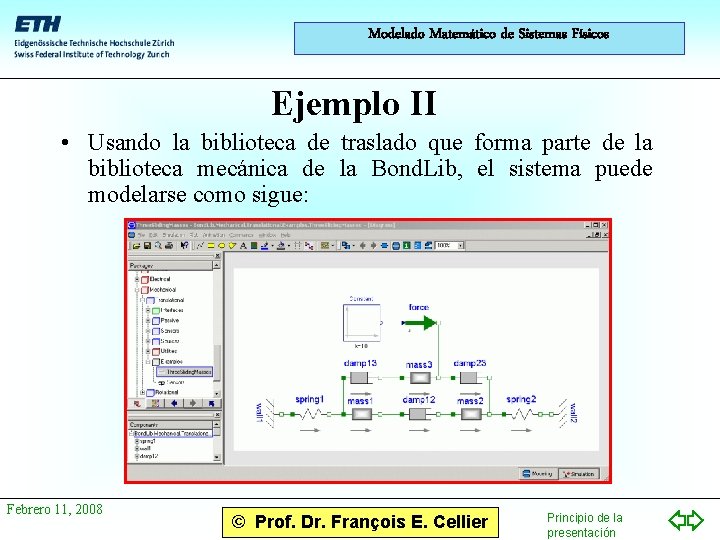
Modelado Matemático de Sistemas Físicos Ejemplo II • Usando la biblioteca de traslado que forma parte de la biblioteca mecánica de la Bond. Lib, el sistema puede modelarse como sigue: Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

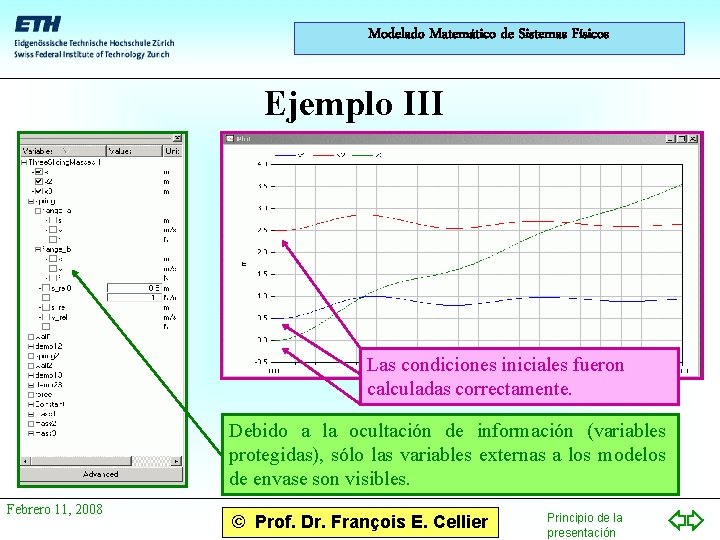
Modelado Matemático de Sistemas Físicos Ejemplo III Las condiciones iniciales fueron calculadas correctamente. Debido a la ocultación de información (variables protegidas), sólo las variables externas a los modelos de envase son visibles. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado • Hasta ahora siempre usamos los voltajes a través de una capacidad y las corrientes a través de una inductancia como variables de estado. • Si tratamos con sistemas multicuerpos, importa mucho la selección de las variables de estado, porque influye fuertemente la eficacia del código de simulación obtenido. • Si seleccionamos las variables de estado bien, el número de ecuaciones de simulación de un sistema multicuerpos estructurado como un árbol crece de forma lineal con el número de grados de libertad. • Si seleccionamos mal las variables de estado, el número de ecuaciones de simulación crece con la cuarta potencia del número de grados de libertad. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado II • Para esto tendríamos que usar las posiciones y velocidades relativas de las articulaciones como variables de estado preferidas. • Dymola soporta el concepto de elegir variables de estado diferentes de aquellas que el sistema usaría normalmente. • Para ello, el usuario puede declarar variables de estado deseadas de la forma siguiente: Real x(state. Select = State. Select. prefer) • Dymola cumplimenta esta instrucción por medio de una versión modificada del algoritmo de Pantelides. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado III • Si la variable de estado deseada ya aparece de forma derivada, úsala si es posible como variable de estado. • Si la variable de estado deseada no aparece aún de forma derivada, se debe derivar la ecuación que evalúa la variable deseada, añadirla al conjunto de las ecuaciones y generar un nuevo integrador para ella. • Ahora tenemos una ecuación superflua. • Si hay variables algebraicas adicionales que se derivan en el proceso de la diferenciación, se derivan las ecuaciones que definen estas variables también y se añaden al conjunto de ecuaciones sin introducir nuevos integradores para ellas. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado IV • En el proceso de estas diferenciaciones adicionales, las nuevas variables y ecuaciones se añaden al conjunto de tal manera que al final del proceso todavía nos queda una ecuación superflua. • Si la variable de estado deseada es legítima, aparece al menos una de las variables de estado seleccionadas antes en el conjunto de las ecuaciones derivadas. • Se elimina el integrador asociado con esta variable del sistema. Ahora tenemos de nuevo el mismo número de ecuaciones y variables. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

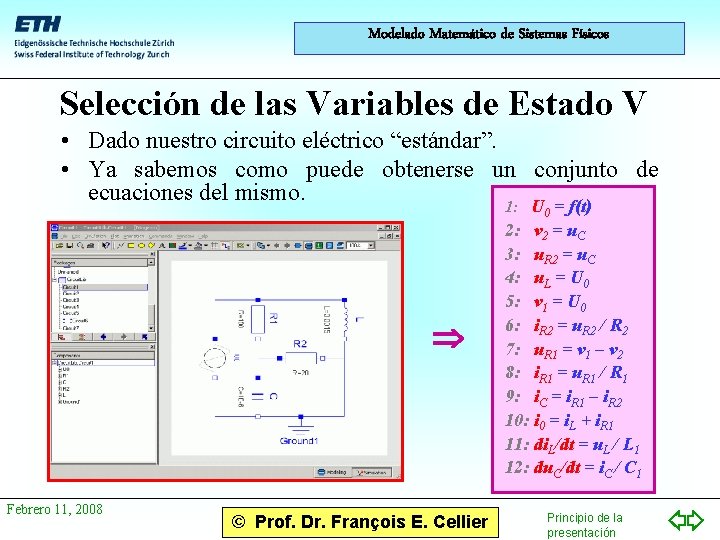
Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado V • Dado nuestro circuito eléctrico “estándar”. • Ya sabemos como puede obtenerse un conjunto de ecuaciones del mismo. 1: U = f(t) 0 Febrero 11, 2008 © Prof. Dr. François E. Cellier 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C/dt = i. C / C 1 Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado VI • Queremos obtener un conjunto modificado de ecuaciones de simulación que use la variable u. R 1 como variable de estado, eliminando una de las variables de estado naturales del conjunto. • Para mostrar el método aplicaremos manualmente el algoritmo de selección de las variables de estado. Febrero 11, 2008 © Prof. Dr. François E. Cellier Principio de la presentación

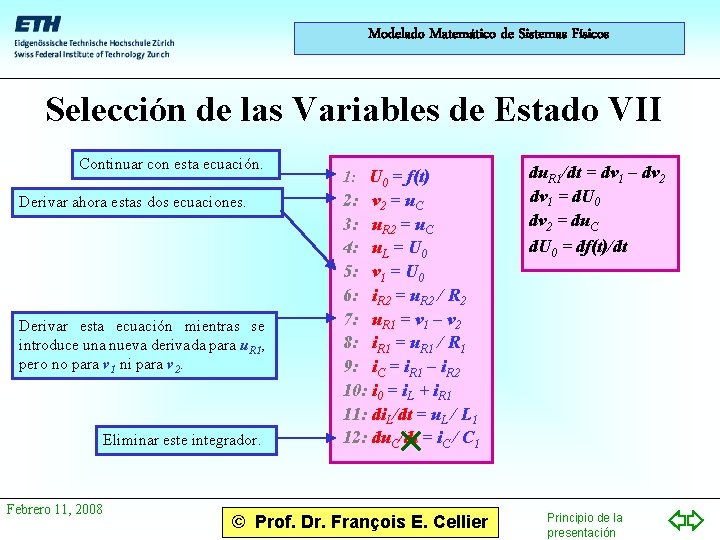
Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado VII Continuar con esta ecuación. Derivar ahora estas dos ecuaciones. Derivar esta ecuación mientras se introduce una nueva derivada para u. R 1, pero no para v 1 ni para v 2. Eliminar este integrador. Febrero 11, 2008 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C/dt = i. C / C 1 © Prof. Dr. François E. Cellier du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado VIII • Ahora se aplica el algoritmo de Tarjan al nuevo conjunto. 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 Febrero 11, 2008 du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 © Prof. Dr. François E. Cellier du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado IX 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 Febrero 11, 2008 du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 © Prof. Dr. François E. Cellier du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado X 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 Febrero 11, 2008 du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 © Prof. Dr. François E. Cellier du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado XI 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 Febrero 11, 2008 du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 © Prof. Dr. François E. Cellier du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt Principio de la presentación

Modelado Matemático de Sistemas Físicos Selección de las Variables de Estado XII 1: U 0 = f(t) 2: v 2 = u. C 3: u. R 2 = u. C 4: u. L = U 0 5: v 1 = U 0 6: i. R 2 = u. R 2 / R 2 7: u. R 1 = v 1 – v 2 8: i. R 1 = u. R 1 / R 1 9: i. C = i. R 1 – i. R 2 10: i 0 = i. L + i. R 1 11: di. L/dt = u. L / L 1 12: du. C = i. C / C 1 Febrero 11, 2008 du. R 1/dt = dv 1 – dv 2 dv 1 = d. U 0 dv 2 = du. C d. U 0 = df(t)/dt • Finalizamos con 16 ecuaciones y 16 incógnitas en lugar de las 12 ecuaciones y 12 incógnitas que había originalmente. • Esta solución es un poco menos eficiente en cuanto al tiempo de ejecución. • Sin embargo, las variables que aparecen derivadas en el modelo son la corriente del inductor i. L y el voltaje en la resistencia u. R 1. © Prof. Dr. François E. Cellier Principio de la presentación