APLICACINES DE LAS DERIVADAS En clculo es importante

APLICACIÓNES DE LAS DERIVADAS. En cálculo es importante conocer el comportamiento de una función f sobre un intervalo dado. ¿El intervalo tiene un valor máximo o un mínimo? ¿Dónde es creciente o decreciente la función? Las derivadas se utilizan para responder a esta preguntas Puntos Críticos. Definición. Decimos que x=c es un punto crítico de la función f(x), si f(c) existe y si lo siguiente es cierto: f’(c)=0 ó f’(c) no existe

Nótese que se requiere que f(c) exista, a fin de que x=c sea un punto crítico. Ejemplo: Determine los puntos críticos de la función: Solución: Encontramos la derivada de la función:

La derivada es un polinomio y es continua en todos los puntos. Los puntos críticos serán aquellos en los cuales la derivada es cero: Por lo tanto los puntos críticos serán: Ejemplo: Determine los puntos críticos de la función: Solución: Reordenando y derivando tendremos:

Nótese que al eliminar el exponente negativo, podemos identificar que t=0 es un punto crítico para esta función, ¿Porque? No existe la derivada. ¿f(c) esta definida en t=0? . Si. por lo tanto t=0 será un punto crítico. Ahora encontremos el punto en el cual la derivada es cero (suponiendo que exista): Reordenando g’(t) obtenemos: En esta expresión racional, ¿en que momento obtenemos un valor de cero en el numerador? Por lo tanto los puntos críticos serán:

Ejemplo: Determine los puntos críticos de la función: Solución: Derivando obtenemos: ¿En que momento podemos considerar que la derivada de esta función no existe? Cuando tengamos un cero en el denominador. Resolviendo tenemos:

Dado que cero al cuadrado siempre es cero, entonces la derivada no existirá en los puntos: w=3 y w=-2 ¿Esta definida la función en estos puntos? No, por lo tanto no son puntos críticos. Debemos recordar que para tener un punto crítico, la función debe existir en este punto. Por lo tanto ¿como encontramos un punto crítico en la derivada de la función? Podemos encontrar los puntos en los que la derivada es cero. ¿Como?

Si, por lo tanto obtendremos dos puntos críticos. Ejemplo: Determine los puntos críticos de la función: Solución: Derivando obtenemos: Factorizando obtenemos:

Esta función es continua en todos los puntos. ¿Como determinamos el momento en que la derivada tiene un valor de cero? Por lo tanto tendremos los siguientes puntos críticos: Ejemplo: Determine los puntos críticos de la función: Solución: Derivando obtenemos:

¿En que momento la derivada no existe? Cuando x tiene un valor negativo o cuando x=0. ¿Serán entonces puntos críticos de la función? No, porque tampoco está definida la función, es decir para f(0). ¿cuál es el valor de la derivada a x=0. Dado que la derivada no existe en x=0, debido a la presencia del logaritmo natural, entonces la derivada tampoco puede ser cero ahí. La derivada solo será cero si igualamos con cero esa parte:

Obteniéndose un solo punto crítico. Valores Máximos y Mínimos. Definición. 1. - Se dice que f(x) tiene un máximo (o global) absoluto en x=c si para cada x en el dominio de la función que se considera. 2. - Se dice que f(x) tiene un máximo (o local) relativo en x=c si para cada x en algún intervalo abierto alrededor de x=c.

3. - Se dice que f(x) tiene un mínimo (o global) absoluto en x=c si para cada x en el dominio de la función que se considera. 2. - Se dice que f(x) tiene un mínimo (o local) relativo en x=c si para cada x en algún intervalo abierto alrededor de x=c. Pautas. Cuando se dice “intervalo abierto alrededor de c”, significa que es posible encontrar un intervalo (a, b), el cual no incluye los puntos finales. Es decir, c estará contenido en dicho intervalo sin ser cualquiera de los puntos finales. Los puntos máximos y mínimos se llaman también los extremos de la función. De tal modo que los extremos relativos serán los máximos y mínimos relativos, mientras que los extremos absolutos serán los máximos y mínimos absolutos. Tendremos un máximo (o mínimo) absoluto en x=c , siempre y cuando f(c) sea el valor mas grande (o mas pequeño) en el dominio de la función considerada.

Todo lo que se requiere para que un punto sea un máximo o mínimo relativo, es que el punto sea un máximo o mínimo en algún intervalo de x’s alrededor de x=c. Puede haber valores de la función mas grandes o menores en algún otro lugar, pero relativo a x=c o local a x=c, f(c) es mas grande o mas pequeño que todos los valores alrededor de c. Los extremos relativos no ocurren en los puntos finales del dominio, solo en el interior del mismo. Por lo tanto es posible buscar valores en el dominio, alrededor de x=c, a fin de verificar que realmente sea un máximo o un mínimo. Esto se puede ver gráficamente:

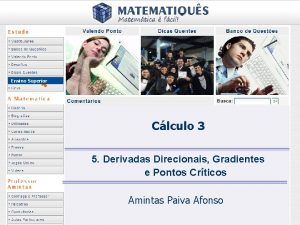
Ejemplo: Identifique en la gráfica los máximos y mínimos, relativos y absolutos. Solución: Máximos relativos en x=b y x=d Mínimo relativo en x=c. ¿ x=e es un mínimo relativo? Máximo absoluto en x=d Mínimo absoluto en x=a

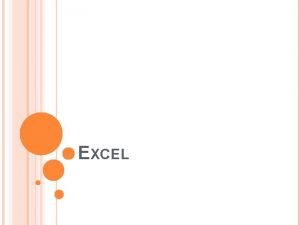
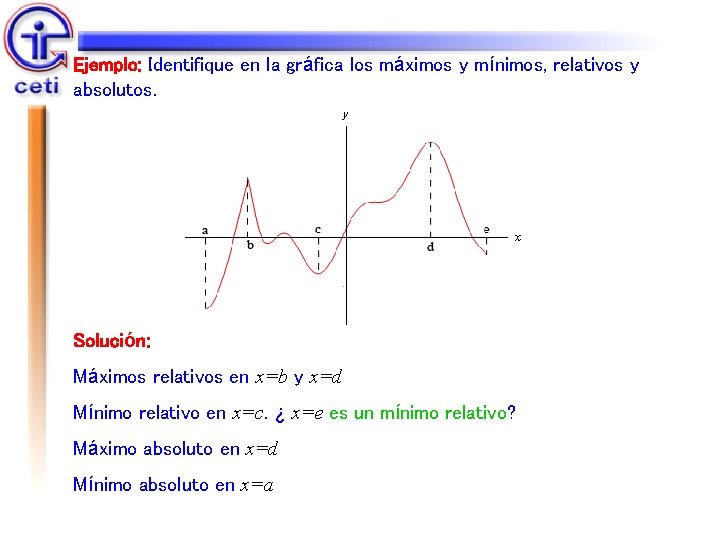
Ejemplo: Identifique los extremos relativos y absolutos de la siguiente función. f(x)=x 2 en Solución: Para [-1, 2] tenemos Mínimo absoluto y relativo en x=0 Máximo absoluto en x=2 ¿x=-1 es un mínimo relativo? La función no tiene máximos relativos [-1, 2]; [-2, 2]

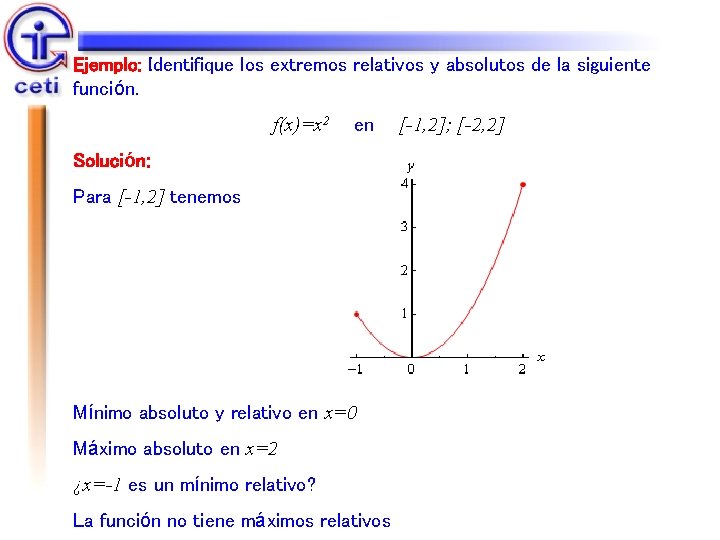
Solución: Para [-2, 2] tenemos Mínimo absoluto y relativo en x=0 Máximos absoluto en x=2 y x=-2 La función no tiene máximos relativos

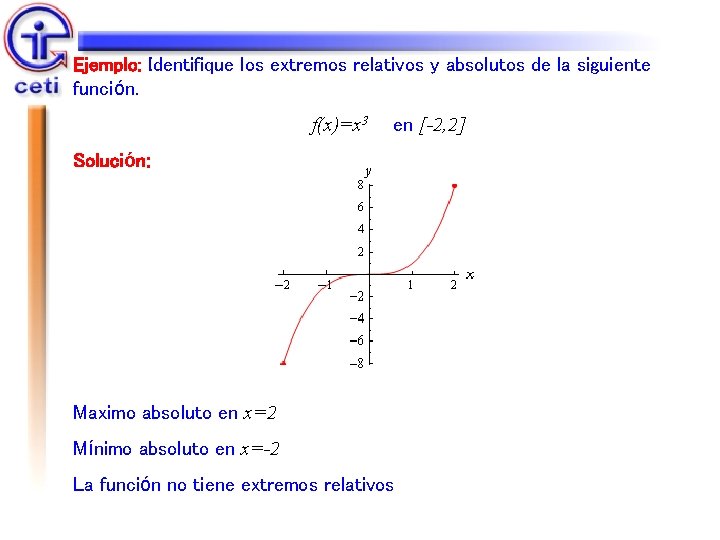
Ejemplo: Identifique los extremos relativos y absolutos de la siguiente función. f(x)=x 3 en [-2, 2] Solución: Maximo absoluto en x=2 Mínimo absoluto en x=-2 La función no tiene extremos relativos

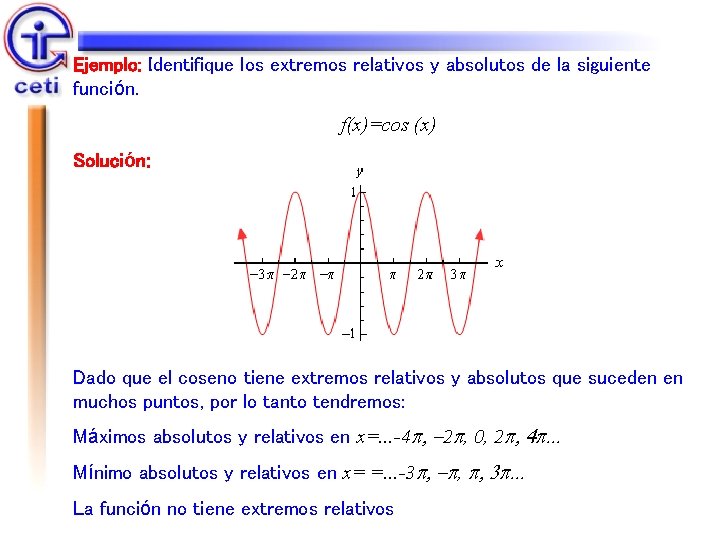
Ejemplo: Identifique los extremos relativos y absolutos de la siguiente función. f(x)=cos (x) Solución: Dado que el coseno tiene extremos relativos y absolutos que suceden en muchos puntos, por lo tanto tendremos: Máximos absolutos y relativos en x=. . . -4 p, -2 p, 0, 2 p, 4 p. . . Mínimo absolutos y relativos en x= =. . . -3 p, -p, p, 3 p. . . La función no tiene extremos relativos

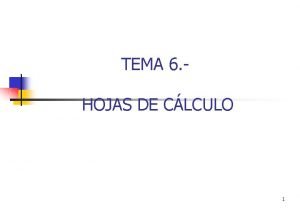
Teorema del Valor Extremo: Suponiendo que f(x) es continua en el intervalo [a, b] entonces habrá dos números tales que f(c) es un máximo absoluto de la función y f(d) es un mínimo absoluto de la función. Pautas Si tenemos una función continua en [a, b] entonces existe la garantía de tener un máximo y un mínimo absolutos para la función en algún lugar del intervalo. El teorema no nos dice nada acerca de extremos absolutos al trabajar sin intervalos. Es imprescindible que la función sea continua en ese intervalo para aplicar el teorema. Teorema de Fermat: Si f(x) tiene un extremo relativo en x=c y f’(c) existe, entonces x=c es un punto crítico de f(x). De hecho este será un punto crítico tal que f’(c)=0.

Pautas Nótese que se dice que f’(c)=0 porque también se supone que f’(c) existe. Este teorema nos muestra que existe una relación entre puntos críticos y extremos relativos. De hecho, nos permitirá obtener una lista de extremos relativos. Ya que un extremo relativo puede ser un punto crítico, una lista de puntos críticos nos dará una lista de los extremos relativos posibles.

Evaluando extremos absolutos. Dada una función continua, f(x), en un intervalo [a, b] se requiere determinar el extremo absoluto de la función. Dado que tenemos un intervalo, y también estamos suponiendo que la función es continua, el Teorema del Valor Extremo nos dice que podemos determinarlo. Hemos visto que los extremos absolutos pueden ocurrir en los puntos terminales, o en un extremo relativo. Así mismo se ha visto, de acuerdo con el Teorema de Fermat, que una lista de puntos críticos, es también una lista de extremos relativos. Debemos recordar por lo tanto que los extremos absolutos no son mas que los valores mas grandes y más pequeños de una función, por lo tanto lo que necesitamos es una lista de posibles extremos absolutos, sustituirlos dentro de la función e identificar el valor más pequeño y el más grande.

Procedimiento para Obtener Extremos Absolutos de f(x) en [a, b] 1. - Verifique la función es continua en el intervalo [a, b]. 2. - Encuentre todos los puntos críticos de f(x), que se encuentran en el intervalo [a, b] 3. - Evalúe la función en los puntos críticos encontrados y en los puntos finales. 4. - Identifique los extremos absolutos. Ejemplo. Determine los extremos absolutos para la siguiente función en el intervalo dado. ¿Es continua la función en el intervalo dado? Las funciones polinomiales son continuas y por lo tanto es continua en este intervalo en particular. ¿Cómo encontramos lo puntos críticos? La derivada de la función nos permite encontrar los puntos críticos.

Entonces los puntos críticos serán: t=-2 y t=1 ¿Estos puntos caen en el intervalo que nos interesa? Si. Debemos recordar que solo nos interesan los puntos críticos que caen en el intervalos en cuestión. Ahora evaluamos la función con los puntos críticos obtenidos y con los puntos terminales. Así que podemos identificar que los valores extremos de g(t) son: Máximo absoluto = 24 el cual se da a t=-2 (un punto crítico). Mínimo absoluto = -28 el cual se da a t=-4, un punto final del intervalo.

Ejemplo. Determine los extremos absolutos para la siguiente función en el intervalo dado. Solución. En el primer ejemplo encontramos que los puntos críticos fueron: t=-2 y t=1 Sin embargo, en este caso debido al intervalo que en que estamos trabajando, nuestro único punto crítico sería t=1. Ahora evaluamos la función en el único punto crítico y en los puntos finales del intervalo. Entonces lo valores extremos serán: Máximo absoluto = 8 en t=2 Mínimo absoluto = -3 en t=1

Ejemplo. Suponga que la cantidad de dinero en una cuenta de banco después de t años, esta dado por: Determine la cantidad máxima y mínima de dinero en la cuenta durante los primeros diez años. Solución. En este caso se está preguntando por los extremos absolutos de A(t) en el intervalo [0, 10]. ¿Es continua la función? Si, y por lo tanto podemos calcular los extremos absolutos. Obtenemos la derivada de la función:

La derivada existe en todos los puntos, y sabemos que el término exponencial nunca es cero. ¿Cómo determinamos los puntos críticos? La derivada únicamente será cero cuando: Obtenemos dos puntos críticos, pero solo nos sirve t=2, por estar dentro del intervalo de interés. Evaluando la función en el punto crítico y en los puntos finales del intervalo obtenemos: Cantidad máxima = 2000 a t=0, y Cantidad mínima = 199. 66 a t=2

Ejemplo. Determine los extremos absolutos para la siguiente función en el intervalo dado. Solución. La función es continua para todas las y’s, por lo tanto podemos obtener los extremos absolutos. Obtenemos la derivada. ¿Cuales serían los puntos críticos?

Tendremos dos puntos críticos: Porque la derivada no existe en este punto, y Porque la derivada es cero en este punto Ambos valores se encuentran en el intervalo, así que evaluando la función en estos puntos, y en los puntos finales tendremos: Máximo absoluto = 0 en y=-4, y Mínimo absoluto = -15 en y=-5

Teorema del Valor Medio: Antes de dar la definición de este teorema, veamos la siguiente definición. Teorema de Rolle. Suponga que f(x) que satisface lo siguiente: 1. - f(x) es continua en el intervalo cerrado [a, b] 2. - f(x) es derivable en el intervalo abierto (a, b) 3. - f(a) = f(b) Entonces existe un número c tal que a<c<b y f’(x)=0. O en otras palabras f(x) tiene un punto crítico en (a, b)

Ejemplo. Encontrar las dos intersecciones en x de: f(x)=x 2 -3 x+2 y demostrar que f’(x)=0 en algún punto entre las intersecciones de x. Solución. Como puede verse, la función es derivable (continua) en toda la recta real. Evaluando las intersecciones obtenemos: x 2 -3 x+2=0 (x-1)(x-2)=0 De tal modo que f(1)=f(2)=0 De acuerdo con el teorema de Rolle se dabe que existe al menos una c en el intervalo (1, 2) tal que f’(c)=0. ¿Cómo determinamos esta c? Derivamos f(x) e igualamos a 0. f’(x)=2 x-3=0 Por lo tanto tendremos que x=3/2 cuando f’(x)=0 Nótese que dicho valor se encuentra en el intervalo abierto (1, 2)

Teorema del Valor Medio (TVM): Suponga que f(x) que satisface lo siguiente: 1. - f(x) es continua en el intervalo cerrado [a, b] 2. - f(x) es derivable en el intervalo abierto (a, b) Entonces existe un número c tal que a<c<b y O Interpretación geométrica del TVM Primero definamos lo siguiente: A=(a, f(a)) y B=(b, f(b)). De acuerdo con el TVM existe una c al que a<c<b y que:

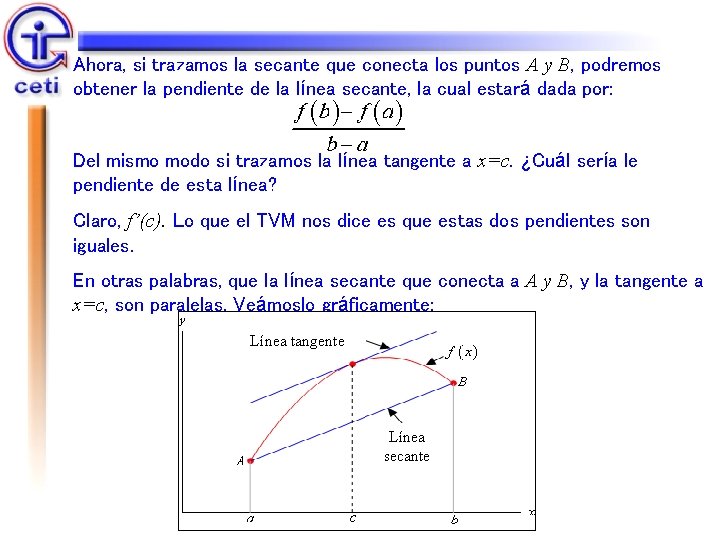
Ahora, si trazamos la secante que conecta los puntos A y B, podremos obtener la pendiente de la línea secante, la cual estará dada por: Del mismo modo si trazamos la línea tangente a x=c. ¿Cuál sería le pendiente de esta línea? Claro, f’(c). Lo que el TVM nos dice es que estas dos pendientes son iguales. En otras palabras, que la línea secante que conecta a A y B, y la tangente a x=c, son paralelas. Veámoslo gráficamente: Línea tangente Línea secante

Ejemplo. Determine todos los números c que satisfagan el Terorema del Valor Medio para la siguiente función: f(x)=x 3 +2 x 2 -x en [-1, 2] Solución. Notemos que f(x) es una función polinomial, por lo tanto continua y derivable en el intervalo dado. Primero encontremos la derivada de la función: f’(x)=3 x 2 +4 x-1 Ahora, para determinar los números que satisfacen la conclusiones del TVM, sustituimos los valores del intervalo en la derivada en: Con lo cual obtenemos la siguiente ecuación cuadrática:

Misma que podemos resolver de la siguiente manera: Con lo cual obtenemos dos valores de c: ¿Cuál número será el apropiado? El que se encuentra dentro del intervalo dado: c=0. 7863 Ejemplo. Supongamos que sabemos que f(x) es continua y diferenciable en el intervalo [-1, 2]. Supongamos a su vez que sabemos que f(6)=-2 y que. ¿Cual es el valor más largo posible para f(15)? Solución. Comencemos con la conclusión del TVM. f(15)-f(6)=f’(c)(15 -6)

Sustituyendo los valores conocidos y reordenando tenemos: f(15)=f(6)+f’(c)(15 -6)=-2+9 f’(c) De manera particular sabemos que: f(15)=-2+9 f’(c) =-2+9(10) =88 . What

OPTIMIZACION. Los problemas de optimización tienen que ver con la búsqueda del valor mas grande y mas pequeño de una función, sujeto a alguna restricción. Esta restricción será alguna condición descrita en forma de ecuación, la cual debe absoluta y positivamente ser cierta no importando cual sea la solución del problema. El primer paso para resolver este tipo de problemas es leer, analizar y entender cuidadosamente el problema. . What Una vez hecho esto, se identifica la cantidad a ser optimizada y la resctricción. Ejemplo. Se necesita cercar un predio. Se tienen 500 ft de materia para cercar y un edificio que límita el predio con uno de sus lados. Determine la dimensiones del predio que encerrará el área mas grande posible. Solución. En este tipo de problemas tendremos dos funciones.

La primera de ellas es la función que en realidad se requiere optimizar, y la segunda es la restricción. Realizar un diagrama que describa la situación es de mucha utilidad. Edificio ¿Qué queremos hacer? Maximizar el área ¿Por lo tanto cual es la función queremos optimizar, y cual es la restricción? Optimizar la función área. La cantidad de material será la restricción. ¿Cuáles son las ecuaciones que describen ambas funciones? Maximizar: A=xy Restricción: 500=x+2 y Sabemos que podemos encontrar los valores máximos y mínimos de una función, siempre y cuando esta tenga una sola variable. En este caso tenemos dos, entonces ¿como procedemos?

Podemos resolver la restricción para alguna de las dos variables, y sustituir esta en la función del área: x=500 -2 y Sustituyendo esta ecuación en la función área obtenemos una función de y: A(y)=(500 -2 y)y=500 y-2 y 2 Ahora bien, queremos encontrar el valor máximo de esta función. ¿Cuál es el intervalo que usaremos? El intervalo sería [0, 250] ¿Porqué? Cuando y=0 la cerca no tiene lados, solo ancho. Cuando y=250 la cerca solo tiene ancho, sin lados. Estos valores solo tienen sentido en la medida en que nos proporcionan los límites de un intervalo, y por el Teorema del valor Extremo podremos encontrar un máximo entre estos dos puntos.

Por lo tanto podemos decir que el valor máximo de una función continua en un intervalo cerrado se dará en los puntos críticos o en los puntos finales. Entonces derivando para encontrar los puntos críticos: A’(y)=500 -4 y Al igualar con cero y resolver esta ecuación obtenemos un solo punto crítico de: y=125 Al sustituir este valor en A(y) obtenemos un área de: A=31250 ft 2 Resultado que sería el área más grande posible. El valor de la otra dimensión será entonces: x=500 -2(125)=250

Existen otros métodos para encontrar el máximo o mínimo de una función, dado que no siempre es fácil aplicar el método del Valor Extremo. Método 1. Empleando el Método del Valor Extremo. 1. Para usar este método, el intervalo de valores óptimos posibles, llamémosle I, debe tener puntos finales finitos. 2. Así mismo, la función a optimizar debe ser continua en I, incluyendo los puntos finales. 3. Una vez que estas condiciones se cumplan, sabemos que el valor óptimo, ya sea un máximo o un mínimo, ocurrirá en cualquiera de los puntos finales del intervalo, o en algún punto crítico dentro del intervalo de posibles soluciones. En dos circunstancias este método no se podrá emplear: 1. El primero contempla que no todos los problemas tendrán un intervalos de soluciones posibles que a su vez tengan puntos finales en ambos lados.

Y la segunda es que muchas de las funciones a optimizar no serán continuas una vez que reducimos la función a una sola variable. Método 2. Empleo del ensayo de la primera derivada. En este método también se necesitará un intervalo de posibles soluciones I. Sin embargo en este caso los puntos finales no necesitan ser finitos. Se requerirá que la función sea continua en el interior de I, y solo necesitaremos que la función sea continua en los puntos finales si la función es finita y que la función realmente exista en el punto final. Supongamos que x=c es un punto de la función f(x) que estamos tratando de optimizar. La prueba de la primera derivada nos dice que si f’(x)>0 inmediatamente a la izquierda de x=c (es decir, la función se está incrementando inmediatamente a la izquierda) y si f’(x)<0 inmediatamente a la derecha de x=c (es decir, la función está decreciendo inmediatamente a la derecha) entonces x=c será un máximo relativo para f(x). Esto no significa necesariamente que el máximo absoluto de f(x) ocurra en x=c.

Supongamos como un hecho que f’(x)>0 para todas la x’s en I tal que x<c , y que f’(x)<0 para todas la x’s en I tal que x>c. Sabemos, en este caso, que la función se incrementa a la izquierda de x=c, siempre y cuando permanezcamos en I, y a la derecha la función decrece. Por lo tanto podemos decir que el máximo absoluto de f(x) en I, ocurrirá en x=c. Ensayo de la Primera Derivada para Encontrar Extremos Absolutos. Sea I el intervalo de posibles soluciones óptimas de f(x), en adición suponga que f(x) es continua en I, excepto posiblemente en los puntos finales. Finalmente suponga que x=c es un punto crítico de f(x), y que c está en el intervalo I. Si restringimos los valores de x a los que se encuentran en I, entonces: Si f’(x)>0 para todas la x<c y si f’(x)<0 para todas la x>c, entonces f(c) será el valor máximo absoluto de f(x) en el intervalo I. Si f’(x)<0 para todas la x<c y si f’(x)>0 para todas la x>c, entonces f(c) será el valor mínimo absoluto de f(x) en el intervalo I.

Método 3. Empleo del Ensayo de la Segunda Derivada para Encontrar Extremos Absolutos. Sea I el intervalo de posibles soluciones óptimas de f(x), en adición suponga que f(x) es continua en I, excepto posiblemente en los puntos finales. Finalmente suponga que x=c es un punto crítico de f(x), y que c está en el intervalo I. Entonces: Si f’’(x)>0 para todas las x’s en I entonces f(c) será el valor mínimo absoluto de f(x) en el intervalo I. Si f’’(x)<0 para todas las x’s en I, entonces f(c) será el valor máximo absoluto de f(x) en el intervalo I. Ejemplo. Se quiere construir una caja cuya base tiene de largo 3 veces su ancho. El material usado para construir la tapa y el fondo cuesta $10/ft 2, y el material usado para los costados cuesta $6/ft 2. Si la caja debe tener un volumen de 50 ft 3, determine las dimensiones que minimizarán el costo de construcción de la caja. Solución. Primero dibujemos un esquema.

Se quiere minimizar el costo de construcción bajo la restricción de que la caja debe tener un volumen de 50 ft 3. Debemos obtener una ecuación que nos relacione los costos de cada uno de los lados con las dimensiones. Entonces: Minimizar: C=10(2 lw)+6(2 wh+2 lh)=60 w 2+48 wh Restricción: 50=lwh=3 w 2 h Como en el ejemplo anterior, se requiere obtener una función con una sola variable, así podemos deshacernos de h con lo siguiente:

Sustituimos h en la función costo C: Ahora obtengamos la primera y segunda derivadas de la función costo: Determinamos los puntos críticos en la primera derivada: Uno es w=0, lo cual es obvio, y también obvio es el hecho de que este valor no tiene sentido, al menos para el problema que nos ocupa. . El otro punto crítico será cuando el numerador tenga un valor de cero: Ya tenemos un solo punto crítico que tiene sentido, ahora debemos verificar que este sea realmente el mínimo absoluto. ¿Cuál método elegimos para la verificación, ¿el ensayo de la primera o segunda derivada? Para evitarnos cálculos innecesarios, empleamos el tercer método.

De este método se desprende que el valor de w que obtuvimos es positivo (para darle sentido al problema, siempre tendríamos que obtener un valor positivo). Por lo tanto sustituyendo en C’’(w) obtenemos que C’’(w)>0 Y concluimos que w=1. 8821 es el mínimo costo absoluto. Ahora encontramos la dimensiones restantes: ¿cuál será el costo mínimo? C(1. 8821)=$637. 60

Ejemplo. Se quiere construir una caja con una base cuadrada y solo se tienen 10 m 2 de material para ser usado en la construcción de la caja. Suponiendo que todo el material se emplee en la construcción, determine el volumen máximo que se obtendrá. Solución. Primero dibujemos un esquema. Queremos maximizar el volumen y la cantidad de material es la restricción, por lo tanto tendremos el siguiente par de ecuaciones: Maximizar: V=lwh=w 2 h Restricción: 10=2 lw+2 wh+2 lh=2 w 2+4 wh Resolviendo la ecuación de restricción para h y sustituyendo en la ecuación de volumen obtenemos:

La primera y segunda derivada serían: Igualando a cero la primera derivada obtenemos: Tenemos dos puntos críticos, de los cuales, al menos para el problema que nos ocupa, solo el positivo tiene sentido. Empleando como criterio la segunda derivada, ¿podemos decir que hemos obtenido el máximo absoluto? Si, puesto que V’’(w)<0. Por lo tanto el volumen será: V(1. 2910)=2, 1517 m 3 ¿En términos de la primera derivada que observamos?

Que si w<1. 2910, entonces V’(w)>0, es decir a la izquierda del punto crítico el volumen se estará incrementando, y del mismo modo si w>1. 2910, entonces V’(w)<0 , es decir a la derecha del punto crítico el volumen estará decreciendo. Y las dimensiones de la caja serán: Ejemplo. Un fabricante necesita manufacturar un cilindro que pueda contener 1. 5 L de líquido. Determine las dimensiones de la lata que minimizarán la cantidad usada en su construcción. Solución. En este problema la restricción es el volumen y la función a minimizar es el área de la lata, es decir, el área de la pared y las tapas de la lata.

un cilindro que pueda contener 1. 5 L de líquido. Determine las dimensiones de la lata que minimizarán la cantidad usada en su construcción. Solución. En este problema la restricción es el volumen y la función a minimizar es el área de la lata, es decir, el área de la pared y las tapas de la lata. Entonces las ecuaciones del volumen y del área del cilindro serán: V=(pr 2)(h)= pr 2 h Las ecuaciones a manejar serán entonces: Minimizar: A=2 prh+2 pr 2 Restricción: 1500=pr 2 h A=2 prh+2 pr 2

Resolviendo la restricción en términos de h y sustituyendo en A tenemos: Obtenemos la derivada: ¿Cuáles son los puntos críticos? r=0 y r=6. 2035 Aplicando el creiterio de la primera derivada podemos darnos cuenta que para de r<6. 2035 obtendremos valores de A’(r)<0 y para valores de r>6. 2035 obtendremos valores de A’(r)>0. Por lo tanto tendremos un mínimo absoluto en r=6. 2035.