APLICACIONES DE LAS DERIVADAS mjp APLICACIONES DE LAS

APLICACIONES DE LAS DERIVADAS

mjp APLICACIONES DE LAS DERIVADAS Aplicaciones de la Derivada Aplicaciones de la Primera Derivada Monotonía (Crecimiento/Decrecimiento) Extremos relativos (Máximos – Mínimos) Aplicaciones de la Segunda Derivada Curvatura (Concavidad/Convexidad) Puntos de inflexión Representación gráfica de funciones Optimización Pág. 2

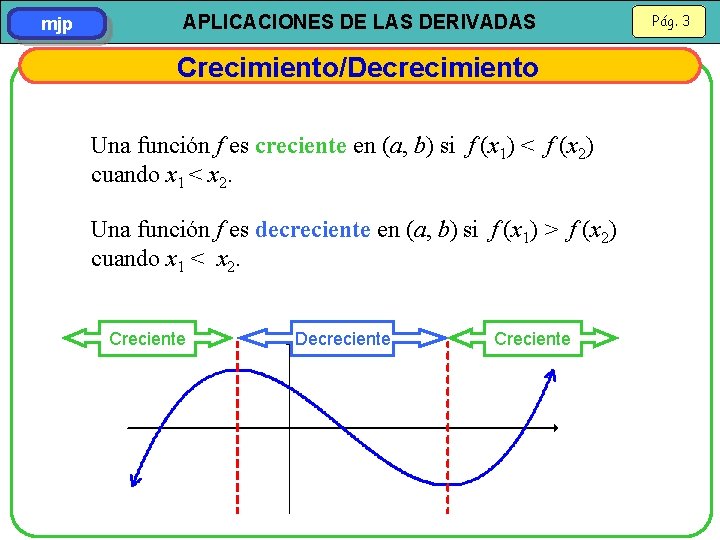
mjp APLICACIONES DE LAS DERIVADAS Crecimiento/Decrecimiento Una función f es creciente en (a, b) si f (x 1) < f (x 2) cuando x 1 < x 2. Una función f es decreciente en (a, b) si f (x 1) > f (x 2) cuando x 1 < x 2. Creciente Decreciente Creciente Pág. 3

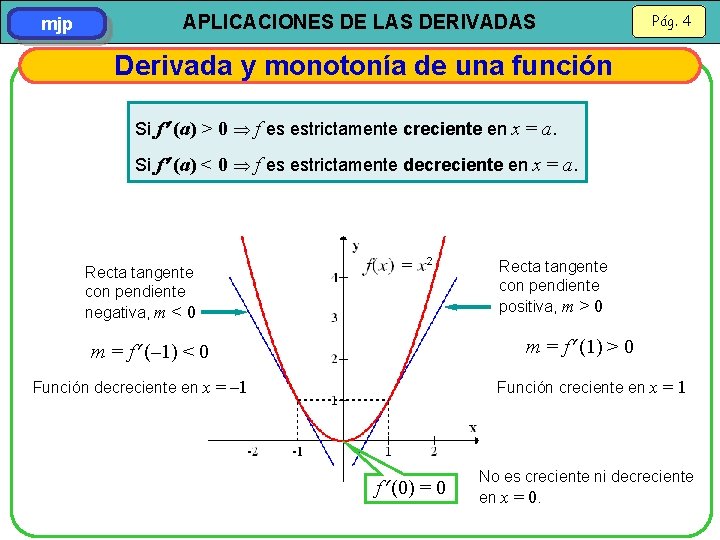
mjp APLICACIONES DE LAS DERIVADAS Pág. 4 Derivada y monotonía de una función Si f (a) > 0 f es estrictamente creciente en x = a. Si f (a) < 0 f es estrictamente decreciente en x = a. Recta tangente con pendiente positiva, m > 0 Recta tangente con pendiente negativa, m < 0 m = f (1) > 0 m = f (– 1) < 0 Función decreciente en x = – 1 Función creciente en x = 1 f (0) = 0 No es creciente ni decreciente en x = 0.

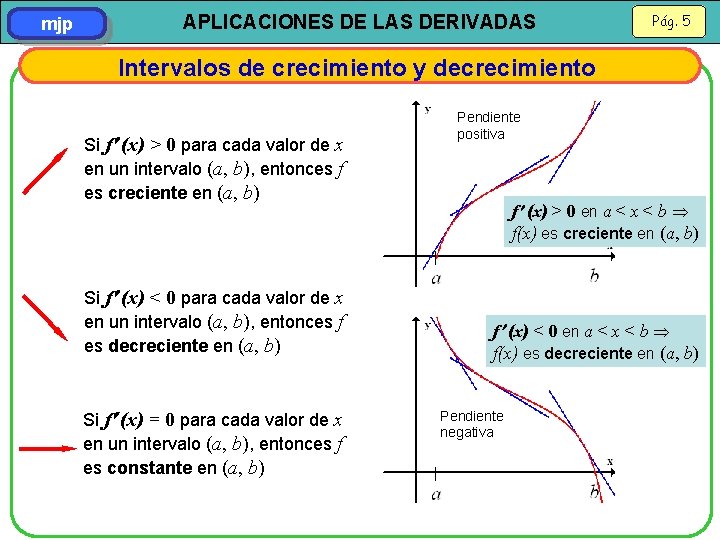
mjp APLICACIONES DE LAS DERIVADAS Pág. 5 Intervalos de crecimiento y decrecimiento Si f (x) > 0 para cada valor de x en un intervalo (a, b), entonces f es creciente en (a, b) Si f (x) < 0 para cada valor de x en un intervalo (a, b), entonces f es decreciente en (a, b) Si f (x) = 0 para cada valor de x en un intervalo (a, b), entonces f es constante en (a, b) Pendiente positiva f (x) > 0 en a < x < b f(x) es creciente en (a, b) f (x) < 0 en a < x < b f(x) es decreciente en (a, b) Pendiente negativa

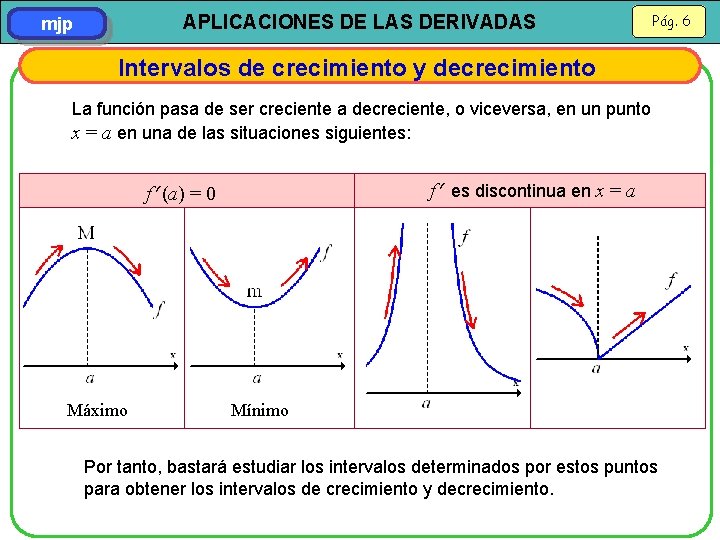
APLICACIONES DE LAS DERIVADAS mjp Pág. 6 Intervalos de crecimiento y decrecimiento La función pasa de ser creciente a decreciente, o viceversa, en un punto x = a en una de las situaciones siguientes: f es discontinua en x = a f (a) = 0 Máximo Mínimo Por tanto, bastará estudiar los intervalos determinados por estos puntos para obtener los intervalos de crecimiento y decrecimiento.

mjp APLICACIONES DE LAS DERIVADAS Intervalos de crecimiento y decrecimiento Diagrama de signos para determinar los intervalos donde f (x) es Crec. /Decr. : 1. Hallar todos los valores de x para los cuales f (x) = 0 o f (x) es discontinua e identificar intervalos abiertos con estos puntos. 2. Prueba un punto c en cada intervalo para obtener el signo de f (c). a. Si f (x) > 0, f es creciente en ese intervalo. b. Si f (x) < 0, f es decreciente en ese intervalo. Pág. 7

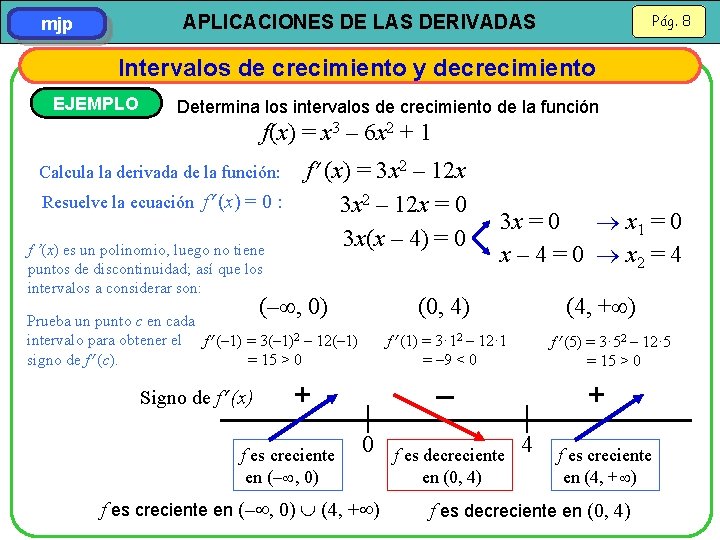
Pág. 8 APLICACIONES DE LAS DERIVADAS mjp Intervalos de crecimiento y decrecimiento EJEMPLO Determina los intervalos de crecimiento de la función f(x) = x 3 – 6 x 2 + 1 f (x) = 3 x 2 – 12 x Resuelve la ecuación f (x) = 0 : 3 x 2 – 12 x = 0 3 x(x – 4) = 0 f ’(x) es un polinomio, luego no tiene Calcula la derivada de la función: puntos de discontinuidad; así que los intervalos a considerar son: (– , 0) (0, 4) Prueba un punto c en cada intervalo para obtener el f (– 1) = 3(– 1)2 – 12(– 1) signo de f (c). = 15 > 0 Signo de f (x) + f es creciente en (– , 0) 3 x = 0 x 1 = 0 x – 4 = 0 x 2 = 4 (4, + ) f (1) = 3· 12 – 12· 1 = – 9 < 0 0 f es creciente en (– , 0) (4, + ) – f es decreciente en (0, 4) f (5) = 3· 52 – 12· 5 = 15 > 0 4 + f es creciente en (4, + ) f es decreciente en (0, 4)

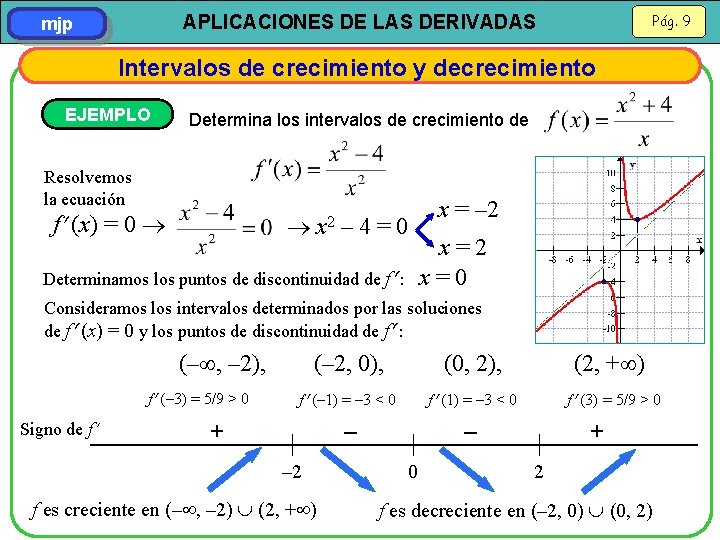
Pág. 9 APLICACIONES DE LAS DERIVADAS mjp Intervalos de crecimiento y decrecimiento EJEMPLO Determina los intervalos de crecimiento de Resolvemos la ecuación f (x) = 0 x 2 – 4=0 x = – 2 x=2 Determinamos los puntos de discontinuidad de f : x = 0 Consideramos los intervalos determinados por las soluciones de f (x) = 0 y los puntos de discontinuidad de f : (– , – 2), f (– 3) = 5/9 > 0 Signo de f + (– 2, 0), (0, 2), (2, + ) f (– 1) = – 3 < 0 f (3) = 5/9 > 0 – – – 2 f es creciente en (– , – 2) (2, + ) 0 2 + f es decreciente en (– 2, 0) (0, 2)

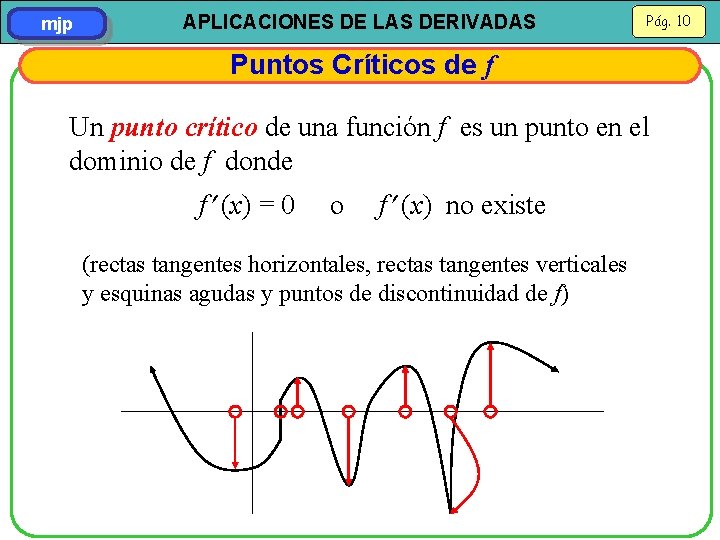
mjp APLICACIONES DE LAS DERIVADAS Pág. 10 Puntos Críticos de f Un punto crítico de una función f es un punto en el dominio de f donde f (x) = 0 o f (x) no existe (rectas tangentes horizontales, rectas tangentes verticales y esquinas agudas y puntos de discontinuidad de f)

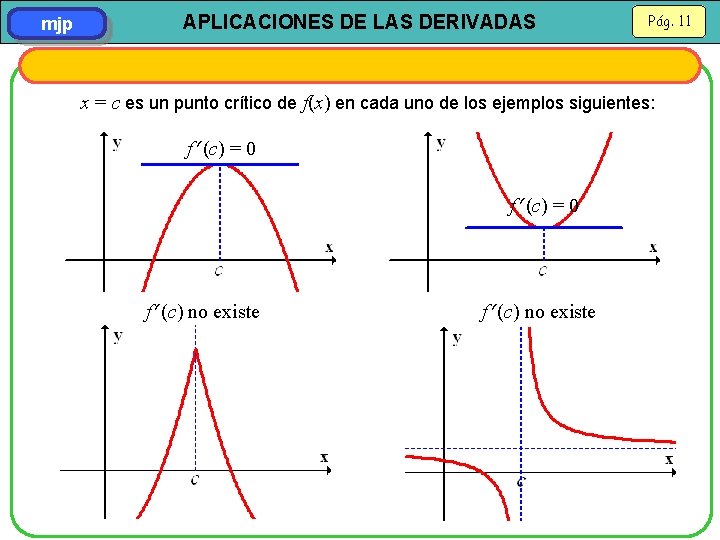
mjp APLICACIONES DE LAS DERIVADAS Pág. 11 x = c es un punto crítico de f(x) en cada uno de los ejemplos siguientes: f (c) = 0 f (c) no existe

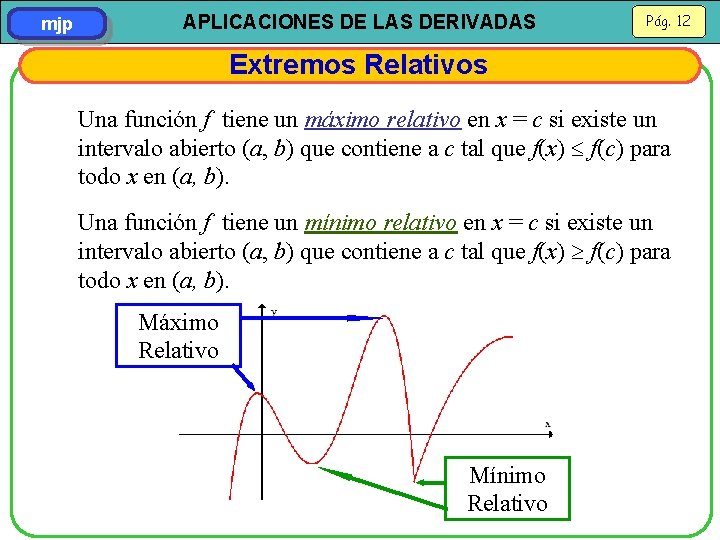
mjp APLICACIONES DE LAS DERIVADAS Pág. 12 Extremos Relativos Una función f tiene un máximo relativo en x = c si existe un intervalo abierto (a, b) que contiene a c tal que f(x) f(c) para todo x en (a, b). Una función f tiene un mínimo relativo en x = c si existe un intervalo abierto (a, b) que contiene a c tal que f(x) f(c) para todo x en (a, b). Máximo Relativo Mínimo Relativo

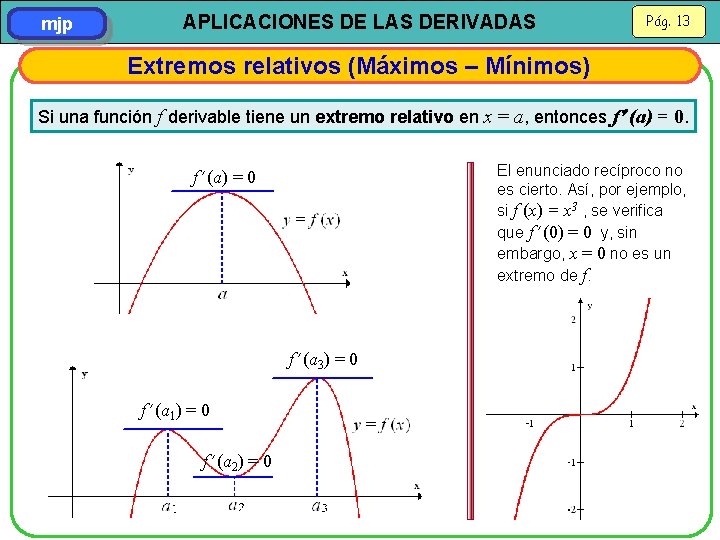
mjp APLICACIONES DE LAS DERIVADAS Pág. 13 Extremos relativos (Máximos – Mínimos) Si una función f derivable tiene un extremo relativo en x = a, entonces f (a) = 0. El enunciado recíproco no es cierto. Así, por ejemplo, si f (x) = x 3 , se verifica que f (0) = 0 y, sin embargo, x = 0 no es un extremo de f. f (a) = 0 f (a 3) = 0 f (a 1) = 0 f (a 2) = 0

mjp APLICACIONES DE LAS DERIVADAS Pág. 14 Extremos relativos (Máximos – Mínimos) Los extremos relativos (Máximos y Mínimos) deberemos buscarlos entre los puntos que son solución de la ecuación f (x) = 0. Veamos como distinguir si un punto en el que la primera derivada se hace cero es máximo o mínimo a partir de: - El signo de la primera derivada a ambos lados del punto. - El signo de la segunda derivada en el punto.

mjp APLICACIONES DE LAS DERIVADAS Pág. 15 Extremos relativos (Máximos – Mínimos) La prueba de la Primera Derivada 1. Determina los puntos críticos de f, en los que f (x) = 0 2. Determina el signo de la derivada de f a la izquierda y a la derecha del punto crítico. Signo de f (x) + – c Signo de f (x) – + c Signo de f (x) + + c Signo de f (x) – c – f(c) es un máximo relativo f(c) es un mínimo relativo f(c) no es extremo relativo

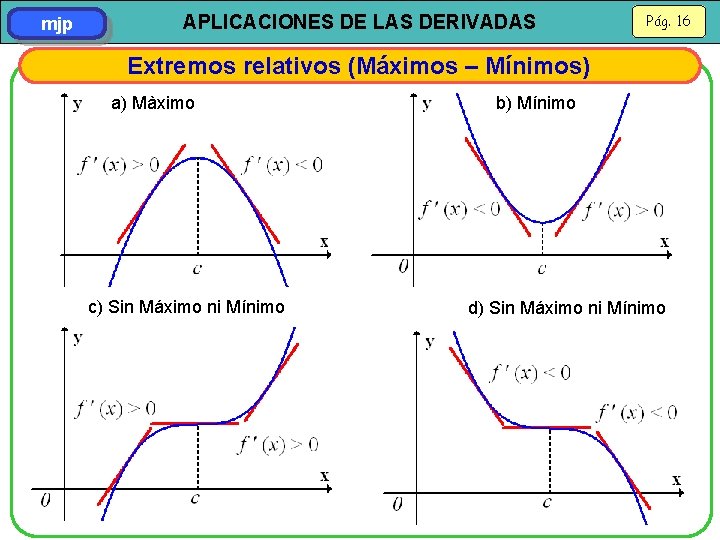
mjp APLICACIONES DE LAS DERIVADAS Pág. 16 Extremos relativos (Máximos – Mínimos) a) Màximo c) Sin Máximo ni Mínimo b) Mínimo d) Sin Máximo ni Mínimo

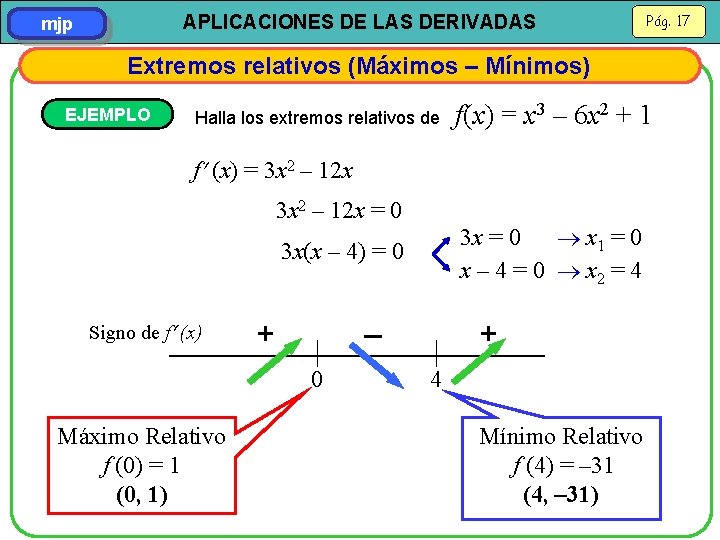
APLICACIONES DE LAS DERIVADAS mjp Pág. 17 Extremos relativos (Máximos – Mínimos) EJEMPLO Halla los extremos relativos de f(x) = x 3 – 6 x 2 + 1 f (x) = 3 x 2 – 12 x = 0 3 x = 0 x 1 = 0 x – 4 = 0 x 2 = 4 3 x(x – 4) = 0 Signo de f (x) Máximo Relativo f (0) = 1 (0, 1) + 0 – 4 + Mínimo Relativo f (4) = – 31 (4, – 31)

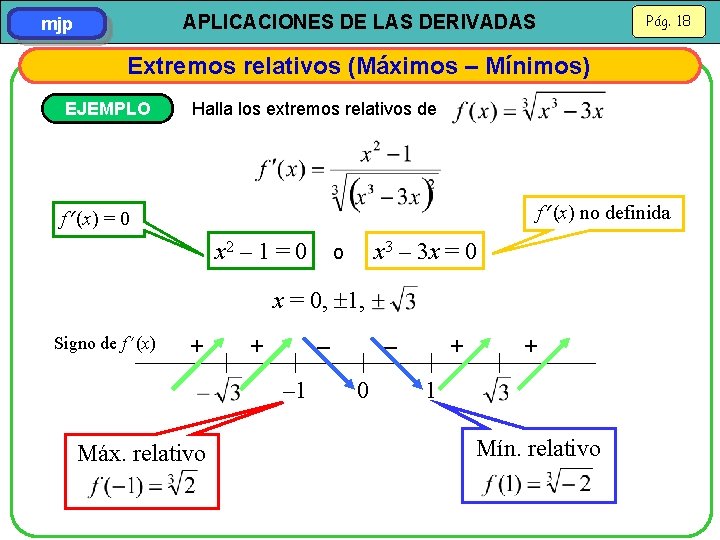
Pág. 18 APLICACIONES DE LAS DERIVADAS mjp Extremos relativos (Máximos – Mínimos) EJEMPLO Halla los extremos relativos de f (x) no definida f (x) = 0 x 2 – 1 = 0 x 3 – 3 x = 0 o x = 0, 1, Signo de f (x) + + – 1 Máx. relativo – 0 – + + 1 Mín. relativo

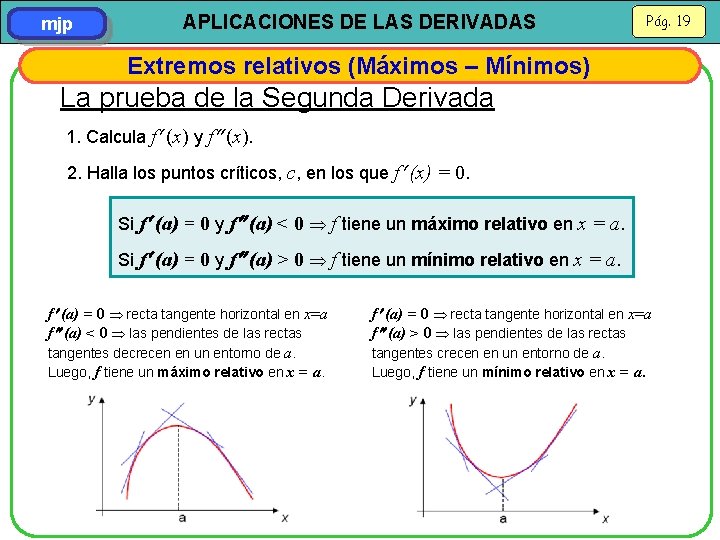
mjp APLICACIONES DE LAS DERIVADAS Pág. 19 Extremos relativos (Máximos – Mínimos) La prueba de la Segunda Derivada 1. Calcula f (x) y f (x). 2. Halla los puntos críticos, c, en los que f (x) = 0. Si f (a) = 0 y f (a) < 0 f tiene un máximo relativo en x = a. Si f (a) = 0 y f (a) > 0 f tiene un mínimo relativo en x = a. f (a) = 0 recta tangente horizontal en x=a f (a) < 0 las pendientes de las rectas tangentes decrecen en un entorno de a. Luego, f tiene un máximo relativo en x = a. f (a) = 0 recta tangente horizontal en x=a f (a) > 0 las pendientes de las rectas tangentes crecen en un entorno de a. Luego, f tiene un mínimo relativo en x = a.

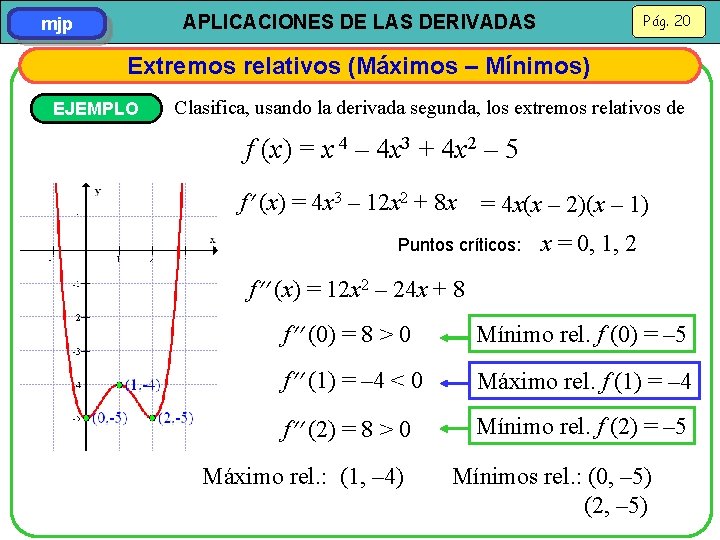
Pág. 20 APLICACIONES DE LAS DERIVADAS mjp Extremos relativos (Máximos – Mínimos) EJEMPLO Clasifica, usando la derivada segunda, los extremos relativos de f (x) = x 4 – 4 x 3 + 4 x 2 – 5 f (x) = 4 x 3 – 12 x 2 + 8 x = 4 x(x – 2)(x – 1) Puntos críticos: x = 0, 1, 2 f (x) = 12 x 2 – 24 x + 8 f (0) = 8 > 0 Mínimo rel. f (0) = – 5 f (1) = – 4 < 0 Máximo rel. f (1) = – 4 f (2) = 8 > 0 Mínimo rel. f (2) = – 5 Máximo rel. : (1, – 4) Mínimos rel. : (0, – 5) (2, – 5)

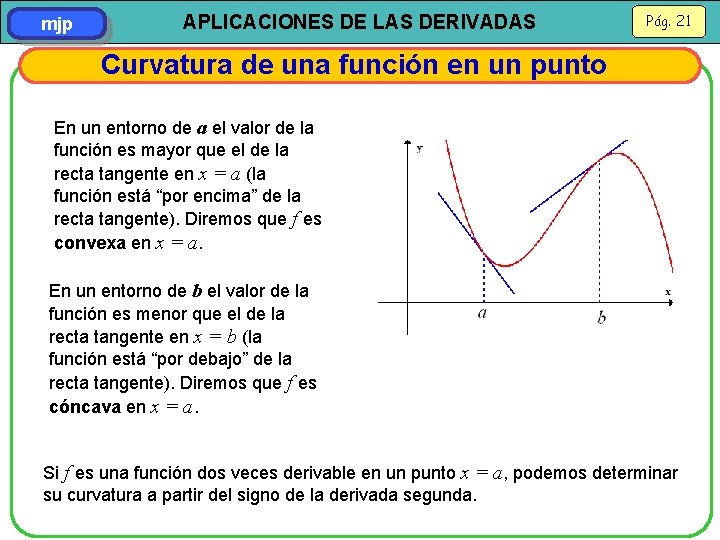
mjp APLICACIONES DE LAS DERIVADAS Pág. 21 Curvatura de una función en un punto En un entorno de a el valor de la función es mayor que el de la recta tangente en x = a (la función está “por encima” de la recta tangente). Diremos que f es convexa en x = a. En un entorno de b el valor de la función es menor que el de la recta tangente en x = b (la función está “por debajo” de la recta tangente). Diremos que f es cóncava en x = a. Si f es una función dos veces derivable en un punto x = a, podemos determinar su curvatura a partir del signo de la derivada segunda.

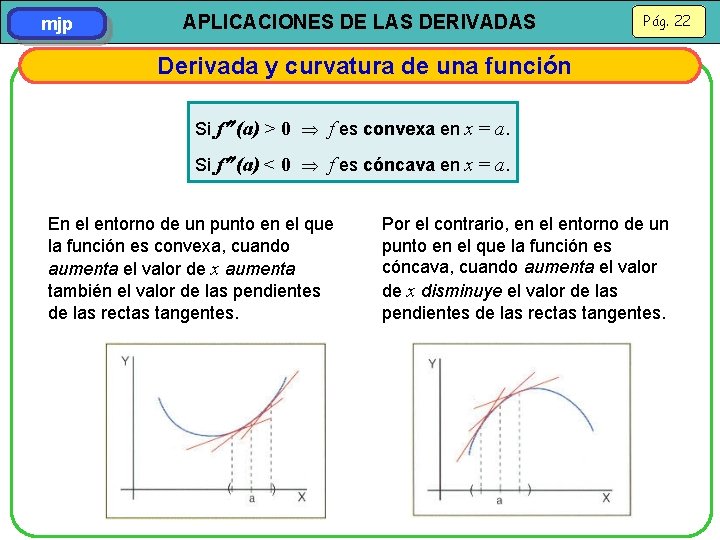
mjp APLICACIONES DE LAS DERIVADAS Pág. 22 Derivada y curvatura de una función Si f (a) > 0 f es convexa en x = a. Si f (a) < 0 f es cóncava en x = a. En el entorno de un punto en el que la función es convexa, cuando aumenta el valor de x aumenta también el valor de las pendientes de las rectas tangentes. Por el contrario, en el entorno de un punto en el que la función es cóncava, cuando aumenta el valor de x disminuye el valor de las pendientes de las rectas tangentes.

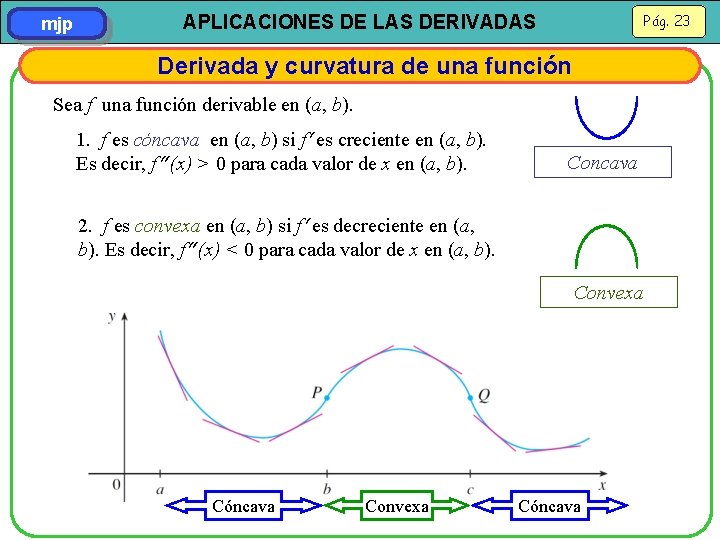
mjp Pág. 23 APLICACIONES DE LAS DERIVADAS Derivada y curvatura de una función Sea f una función derivable en (a, b). 1. f es cóncava en (a, b) si f es creciente en (a, b). Es decir, f (x) > 0 para cada valor de x en (a, b). Concava 2. f es convexa en (a, b) si f es decreciente en (a, b). Es decir, f (x) < 0 para cada valor de x en (a, b). Convexa Cóncava

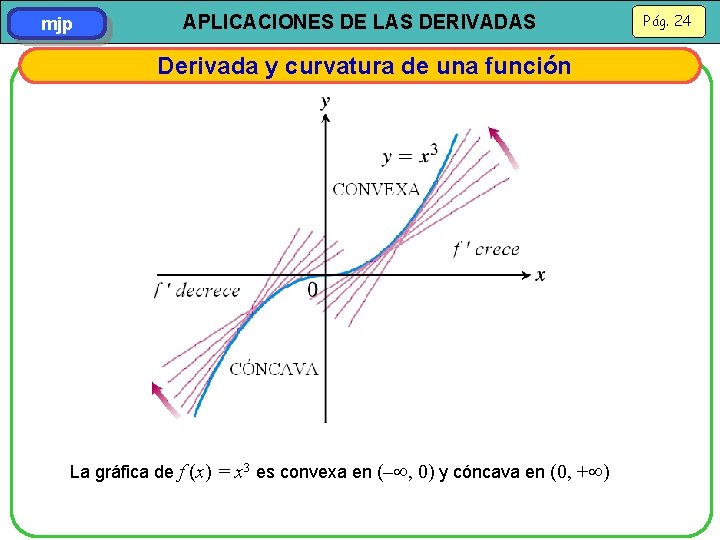
mjp APLICACIONES DE LAS DERIVADAS Derivada y curvatura de una función La gráfica de f (x) = x 3 es convexa en (– , 0) y cóncava en (0, + ) Pág. 24

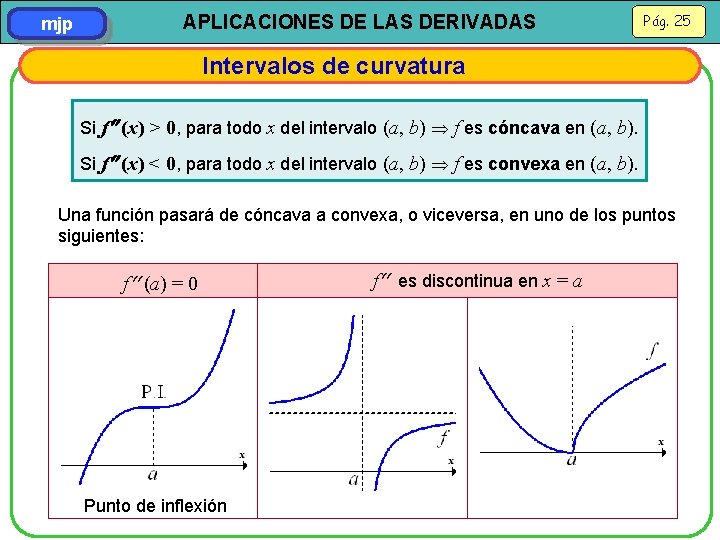
mjp APLICACIONES DE LAS DERIVADAS Pág. 25 Intervalos de curvatura Si f (x) > 0, para todo x del intervalo (a, b) f es cóncava en (a, b). Si f (x) < 0, para todo x del intervalo (a, b) f es convexa en (a, b). Una función pasará de cóncava a convexa, o viceversa, en uno de los puntos siguientes: f (a) = 0 Punto de inflexión f es discontinua en x = a

mjp APLICACIONES DE LAS DERIVADAS Intervalos de curvatura Determinar los Intervalos de Curvatura 1. Determina los valores para los que la segunda derivada de f es cero o no definida. Identifica los intervalos abiertos con estos puntos. 1. Determina el signo de f en cada intervalo del paso 1 probando un punto, c , de cada intervalo. f (c) > 0 f es cóncava en el intervalo. f (c) < 0 f es convexa en el intervalo. Pág. 26

APLICACIONES DE LAS DERIVADAS mjp Intervalos de curvatura EJEMPLO Determina los intervalos de curvatura de la función f(x) = x 3 – 6 x 2 + 1 f (x) = 3 x 2 – 12 x f (x) = 6 x – 12 = 6(x – 2) f (x) = 0 6(x – 2) = 0 x = 2 Signo de f f convexa en (– , 2) – 2 + f cóncava en (2, ) Pág. 27

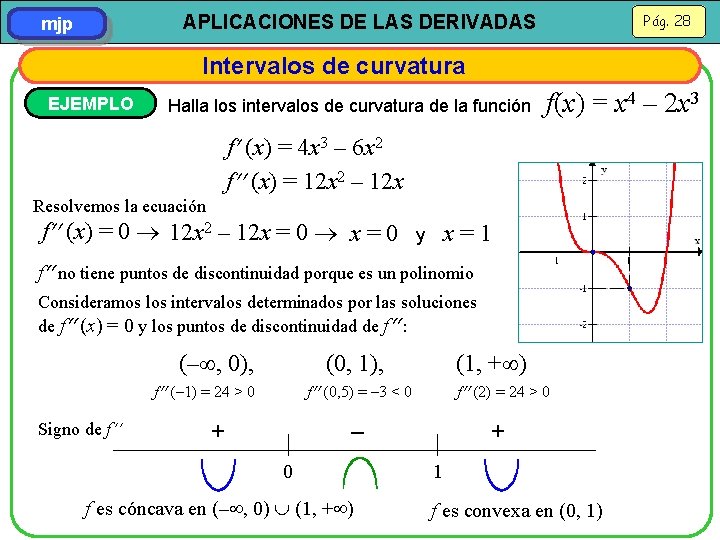
Pág. 28 APLICACIONES DE LAS DERIVADAS mjp Intervalos de curvatura EJEMPLO Halla los intervalos de curvatura de la función f(x) = x 4 – 2 x 3 f (x) = 4 x 3 – 6 x 2 f (x) = 12 x 2 – 12 x Resolvemos la ecuación f (x) = 0 12 x 2 – 12 x = 0 y x=1 f no tiene puntos de discontinuidad porque es un polinomio Consideramos los intervalos determinados por las soluciones de f (x) = 0 y los puntos de discontinuidad de f : (– , 0), (0, 1), f (– 1) = 24 > 0 Signo de f + (1, + ) f (0, 5) = – 3 < 0 0 – f es cóncava en (– , 0) (1, + ) f (2) = 24 > 0 1 + f es convexa en (0, 1)

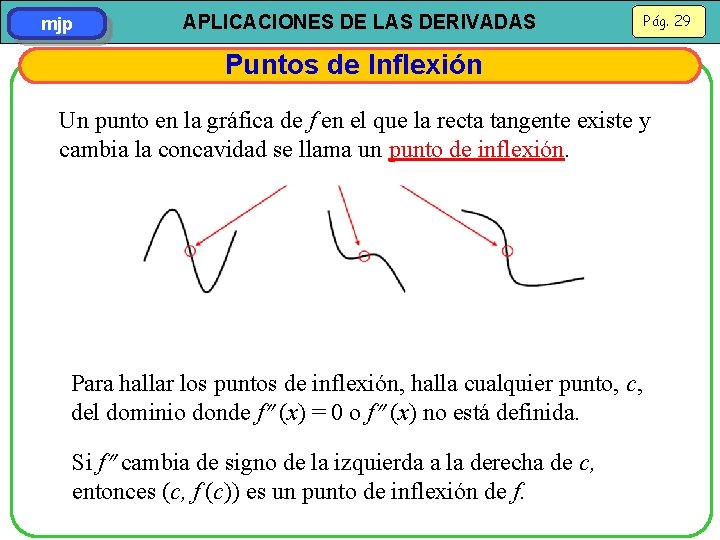
mjp APLICACIONES DE LAS DERIVADAS Pág. 29 Puntos de Inflexión Un punto en la gráfica de f en el que la recta tangente existe y cambia la concavidad se llama un punto de inflexión. Para hallar los puntos de inflexión, halla cualquier punto, c, del dominio donde f (x) = 0 o f (x) no está definida. Si f cambia de signo de la izquierda a la derecha de c, entonces (c, f (c)) es un punto de inflexión de f.

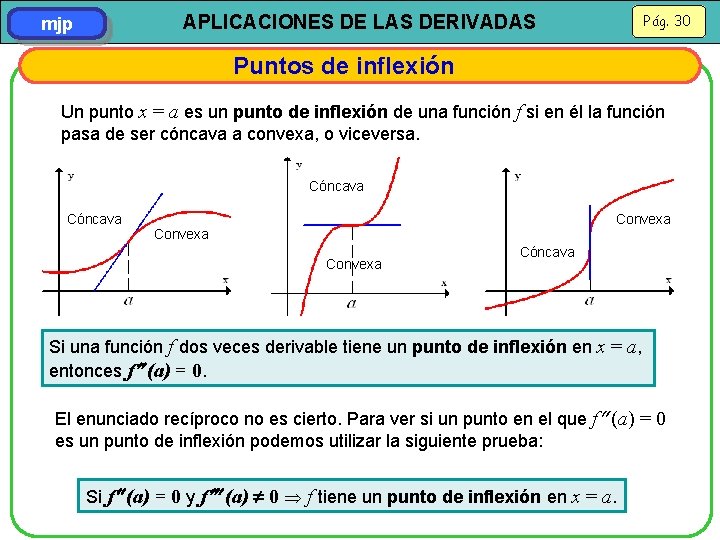
Pág. 30 APLICACIONES DE LAS DERIVADAS mjp Puntos de inflexión Un punto x = a es un punto de inflexión de una función f si en él la función pasa de ser cóncava a convexa, o viceversa. Cóncava Convexa Cóncava Si una función f dos veces derivable tiene un punto de inflexión en x = a, entonces f (a) = 0. El enunciado recíproco no es cierto. Para ver si un punto en el que f (a) = 0 es un punto de inflexión podemos utilizar la siguiente prueba: Si f (a) = 0 y f (a) 0 f tiene un punto de inflexión en x = a.

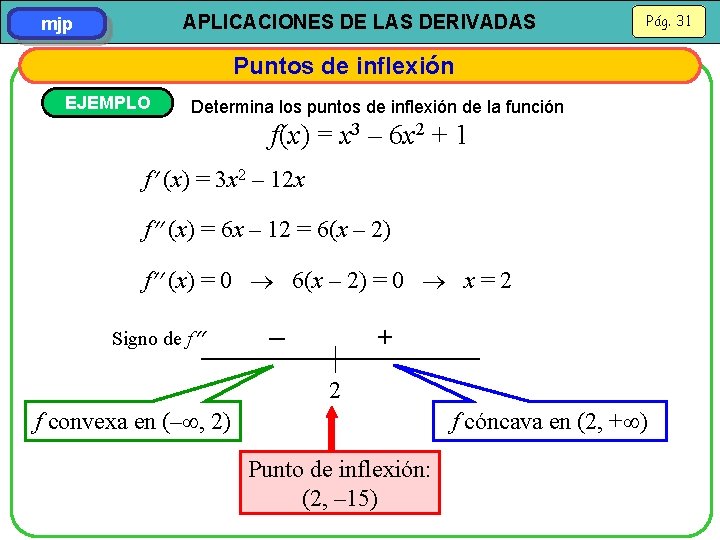
APLICACIONES DE LAS DERIVADAS mjp Pág. 31 Puntos de inflexión EJEMPLO Determina los puntos de inflexión de la función f(x) = x 3 – 6 x 2 + 1 f (x) = 3 x 2 – 12 x f (x) = 6 x – 12 = 6(x – 2) f (x) = 0 6(x – 2) = 0 x = 2 Signo de f – 2 + f convexa en (– , 2) f cóncava en (2, + ) Punto de inflexión: (2, – 15)

mjp APLICACIONES DE LAS DERIVADAS Pág. 32 Asíntotas Verticales La recta x = a es una asíntota vertical de la gráfica de la función f si lím f (x) = x a– o lím f (x) = x a+ Asíntotas Horizontales La recta y = b es una asíntota horizontal de la gráfica de la función f si lím f (x) = b x – o lím f (x) = b x +

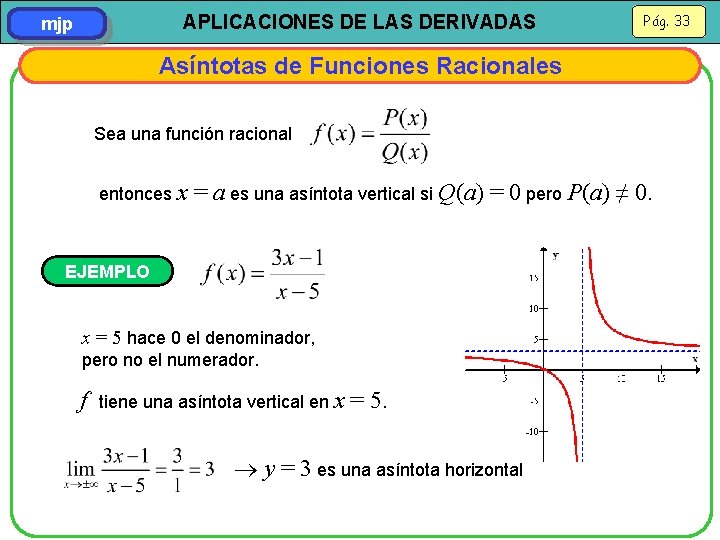
APLICACIONES DE LAS DERIVADAS mjp Pág. 33 Asíntotas de Funciones Racionales Sea una función racional entonces x = a es una asíntota vertical si Q(a) = 0 pero P(a) ≠ 0. EJEMPLO x = 5 hace 0 el denominador, pero no el numerador. f tiene una asíntota vertical en x = 5. y = 3 es una asíntota horizontal

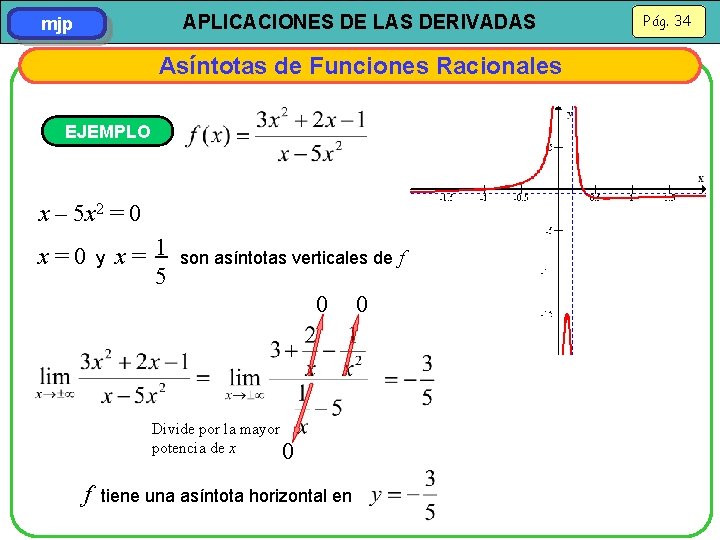
APLICACIONES DE LAS DERIVADAS mjp Asíntotas de Funciones Racionales EJEMPLO x – 5 x 2 = 0 x=0 y x= 1 5 son asíntotas verticales de f 0 Divide por la mayor potencia de x 0 f tiene una asíntota horizontal en 0 Pág. 34

APLICACIONES DE LAS DERIVADAS mjp Representación gráfica de funciones Esquema para trazar curvas 1. 2. 3. 4. 5. 6. 7. 8. 9. Dominio de f. Puntos de corte con los ejes de f, si es posible. Comportamiento en el infinito de f. Asíntotas horizontales y verticales. Intervalos donde f es creciente/decrec. Extremos relativos de f. Concavidad de f. Puntos de inflexión de f. Dibuja f, usa puntos adicionales si es necesario. Pág. 35

APLICACIONES DE LAS DERIVADAS mjp EJEMPLO Dibuja la gráfica de: f (x) = x 3 – 6 x 2 + 9 x +1 1. Dominio: (− , ). 2. Puntos de corte con los ejes: (0, 1) 3. lím f (x) = + x + y lím f (x) = – x – 4. No tiene asíntotas 5. f (x) = 3 x 2 – 12 x + 9 f crec. en (− , 1) (3, ), dec. en (1, 3) 6. Máximo relativo: (1, 5); mínimo relativo: (3, 1) 7. f (x) = 6 x – 12 f convexa en (− , 2); cóncava en (2, + ). 8. Punto de Inflexión: (2, 3) Pág. 36

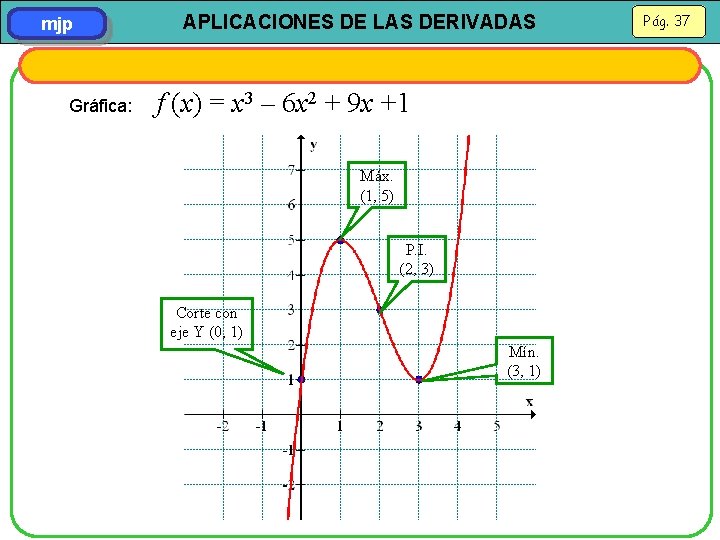
mjp Gráfica: APLICACIONES DE LAS DERIVADAS f (x) = x 3 – 6 x 2 + 9 x +1 Máx. (1, 5) P. I. (2, 3) Corte con eje Y (0, 1) Mín. (3, 1) Pág. 37

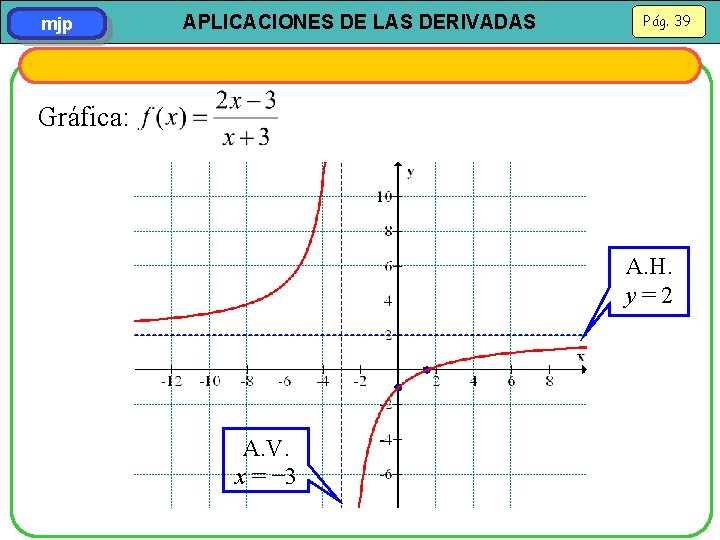
APLICACIONES DE LAS DERIVADAS mjp EJEMPLO Dibuja: 1. Dominio: x − 3 2. Puntos de corte con los ejes: (0, − 1) y (3/2, 0) 3. 4. Asíntotas Horizontal: y = 2; Vertical: x = − 3 5. f es creciente en (− , − 3) (− 3, + ). 6. No tiene extremos relativos. 7. f es cóncava hacia abajo en (− 3, ) y cóncava hacia arriba en (− , − 3). 8. No tiene puntos de inflexión Pág. 38

mjp APLICACIONES DE LAS DERIVADAS Pág. 39 Gráfica: A. H. y=2 A. V. x = − 3

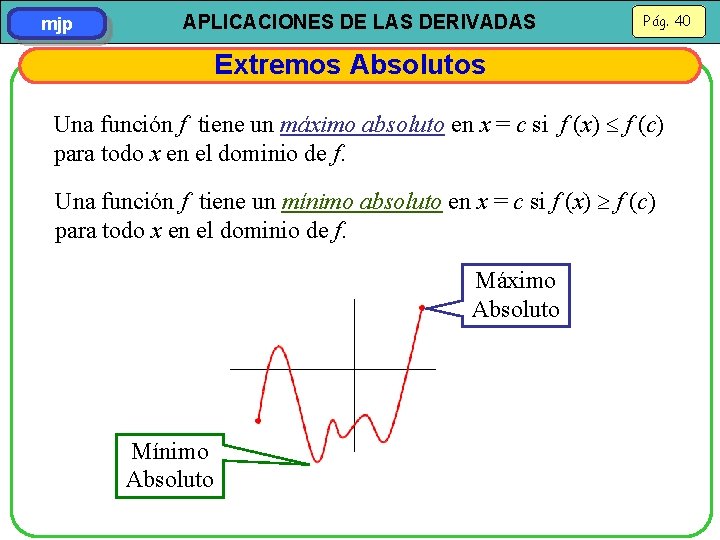
mjp APLICACIONES DE LAS DERIVADAS Pág. 40 Extremos Absolutos Una función f tiene un máximo absoluto en x = c si f (x) f (c) para todo x en el dominio de f. Una función f tiene un mínimo absoluto en x = c si f (x) f (c) para todo x en el dominio de f. Máximo Absoluto Mínimo Absoluto

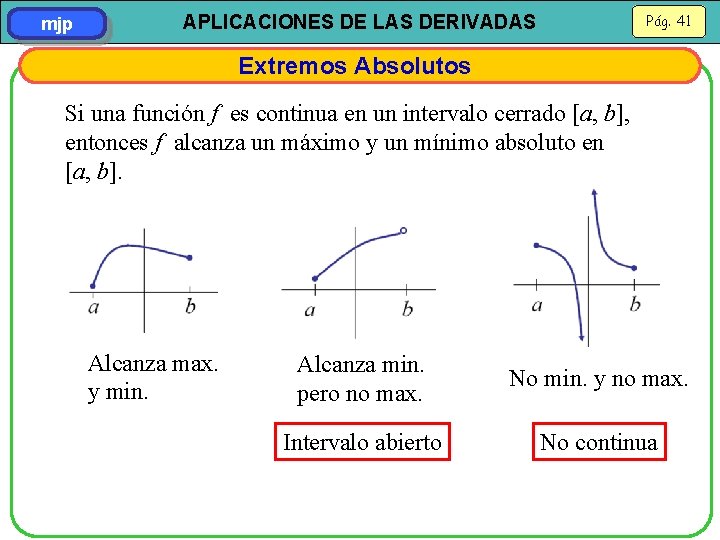
mjp Pág. 41 APLICACIONES DE LAS DERIVADAS Extremos Absolutos Si una función f es continua en un intervalo cerrado [a, b], entonces f alcanza un máximo y un mínimo absoluto en [a, b]. Alcanza max. y min. Alcanza min. pero no max. No min. y no max. Intervalo abierto No continua

Pág. 42 APLICACIONES DE LAS DERIVADAS mjp Extremos Absolutos en un Intervalo Cerrado Para hallar los extremos absolutos de una función f en un intervalo cerrado [a, b] 1. Halla los puntos críticos de f en (a, b). 2. Calcula f en cada punto crítico y en los extremos del intervalo: Mayor valor = Máximo Absoluto Menor valor = Mínimo Absoluto EJEMPLO Halla los extremos absolutos de f (x) = x 3 – 3 x 2 f (x) = 3 x 2 – 6 x = 3 x(x – 2) Valores críticos en x = 0, x = 2 f (0) = 0 f (2) = – 4 Mín. Absoluto f (4) = 16 Máx. Absoluto Evalúa en

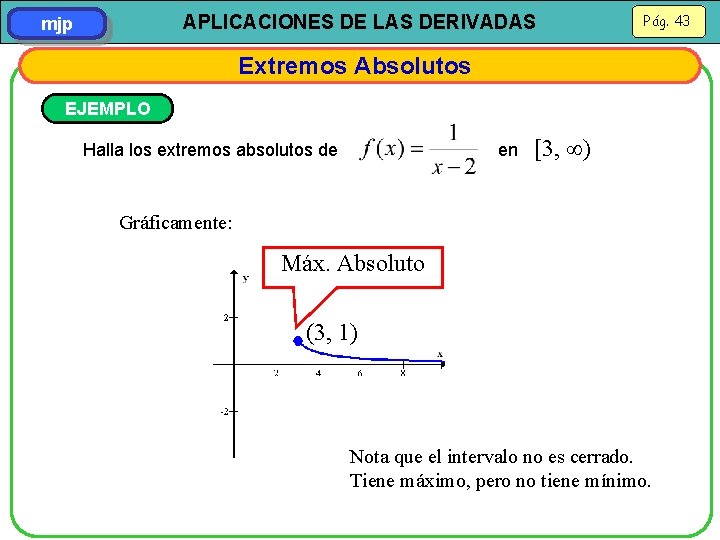
APLICACIONES DE LAS DERIVADAS mjp Pág. 43 Extremos Absolutos EJEMPLO Halla los extremos absolutos de en [3, ) Gráficamente: Máx. Absoluto (3, 1) Nota que el intervalo no es cerrado. Tiene máximo, pero no tiene mínimo.

mjp APLICACIONES DE LAS DERIVADAS Problemas de Optimización 1. Asigna una letra a cada variable mencionada en el problema. Un dibujo pude ayudar. 1. Encuentra una expresión para la cantidad a optimizar. 1. Usa las condiciones para escribir la expresión como una función en una variable (observa cualquier restricción del dominio). 4. Optimiza la función. Pág. 44

APLICACIONES DE LAS DERIVADAS mjp Pág. 45 Problemas de Optimización EJEMPLO Una caja abierta por arriba se forma cortando cuadrados idénticos en las esquinas de un cartón cuadrado de 4 dm por 4 dm. Calcula las dimensiones de la caja que hacen que su volumen sea máximo. x V = largo·ancho·alto = (4 – 2 x)x; 4 – 2 x x x en [0, 2] V(x) = 16 x – 16 x 2 + 4 x 3 V (x) = 16 – 32 x + 12 x 2 = 0 Puntos críticos: x = 2, x = 2/3 V(2) = 0 V(0) = 0 V(2/3) 4, 74 dm 2 Las dimensiones son 8/3 dm por 2/3 dm que dan cajas de volumen máximo de 4. 74 dm 3.

APLICACIONES DE LAS DERIVADAS mjp Pág. 46 Problemas de Optimización EJEMPLO Una compañía estima que la demanda de un producto fluctúa con su precio. La función de demanda es q = 1800 − 2 p donde q es el número de unidades demandadas y p el precio de cada unidad. El costo total de producir q unidades es C(q) = 135000 + 6 q + 0, 1 q 2 a) Hallar cuántas unidades q deben producirse para maximizar el beneficio. b) Hallar el precio que debe fijarse. c) Hallar el beneficio esperado. Solución El beneficio es igual a los ingresos menos los costos. La función de costos la tenemos. Debemos expresar la función de ingreso I. Sabemos que el ingreso es el producto de las unidades vendidas por el precio de cada una, I = p · q. El problema se debe resolver en términos de las unidades q, así que obtenemos p de la ecuación de demanda:

mjp APLICACIONES DE LAS DERIVADAS Pág. 47 Problemas de Optimización Reemplazando en la función de ingreso: El Beneficio B es Ingresos menos Costos: B(q) = I(q) – C(q) B(q) = 894 q – 0, 6 q 2 – 135000 a) Para obtener el máximo derivamos e igualamos a cero: B (q) = 894 – 1, 2 q = 0 q = 745 Como la segunda derivada B (q) < 0 siempre, estamos en presencia de un máximo. Así, el número de unidades que proporciona el máximo beneficio es de 745. b) Al reemplazar las unidades en la función de demanda tendremos el precio que debe fijarse: 745 = 1800 − 2 p p = 527, 5 € c) El beneficio esperado es B(745) = 894· 745 -0, 6· 7452 – 350 = = 666030 – 333015 – 135000 = 198015 €

APLICACIONES DE LAS DERIVADAS mjp Pág. 48 Problemas de Optimización EJEMPLO En un día desapacible, la temperatura T en grados centígrados varió con el tiempo t en horas según la función T (t) = t 2 – 9 t + 8 para 0 t 12. a) Calcula la temperatura a las dos de la mañana. b) ¿Cuál fue la temperatura mínima? ¿A qué hora? c) ¿A qué hora hubo 0 grados? d) Halla T (2) y explica su significado. e) Representa gráficamente la función. Solución a) Como T (t) = t 2 – 9 t + 8 , 0 t 12, la temperatura a las dos de la mañana, T(2), será: T (2) = 22 – 9· 2 + 8 = – 6 ºC b) Hallamos T (t) = 2 t – 9 = 0 t = 4, 5 A las 4, 5 horas se alcanzó la temperatura mínima de T(4, 5) = – 12, 25 ºC

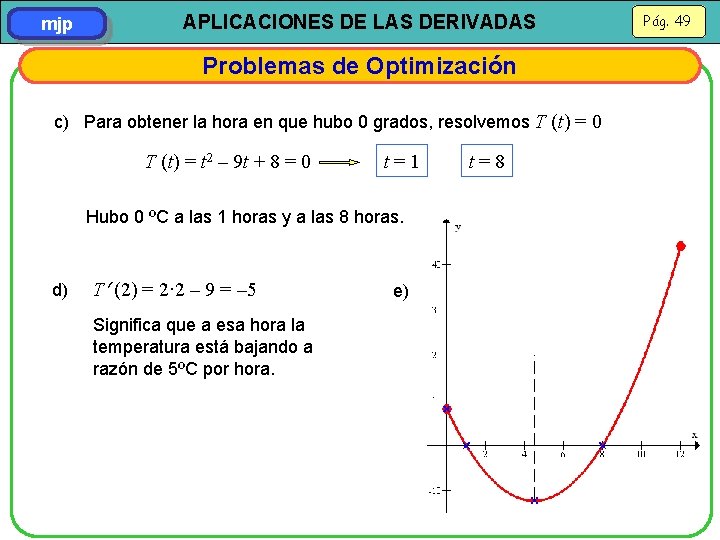
mjp APLICACIONES DE LAS DERIVADAS Problemas de Optimización c) Para obtener la hora en que hubo 0 grados, resolvemos T (t) = 0 T (t) = t 2 – 9 t + 8 = 0 t=1 Hubo 0 ºC a las 1 horas y a las 8 horas. d) T (2) = 2· 2 – 9 = – 5 Significa que a esa hora la temperatura está bajando a razón de 5ºC por hora. e) t=8 Pág. 49

mjp APLICACIONES DE LAS DERIVADAS EJERCICIOS Página 180 – 183 nº 1 - 46 Autoevaluación Pág. 50