Mximos y Mnimos Puntos de una grfica o

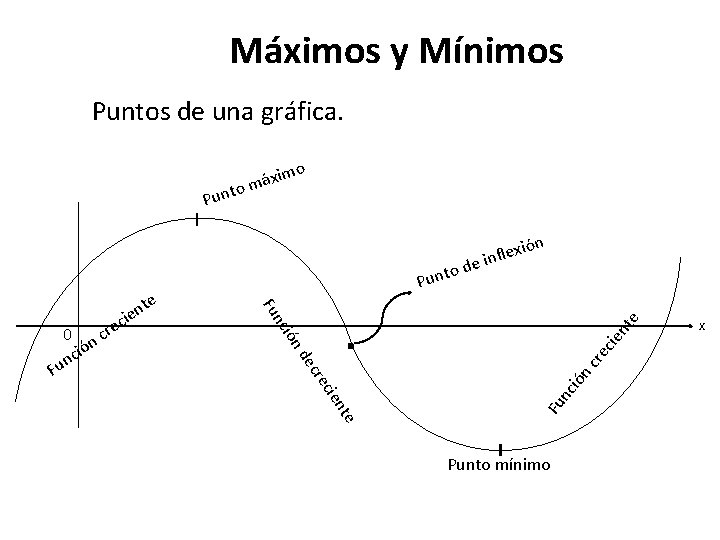
Máximos y Mínimos Puntos de una gráfica. o xim á m o Punt Fu d cr ión nc Fu te ien rec ec nd ec ie nt e . ió nc 0 n ció n Fu c e r c te n ie o Punt ón lexi f n i e Punto mínimo x

Métodos para encontrar estos puntos: Ø Máximos y mínimos • Criterio de la primera derivada. • Criterio de la segunda derivada. Ø Punto de inflexión • Criterio de la segunda derivada. Ø Sentido de la concavidad • Criterio de la segunda derivada. Ø Función creciente y decreciente • Criterio de la primera derivada.

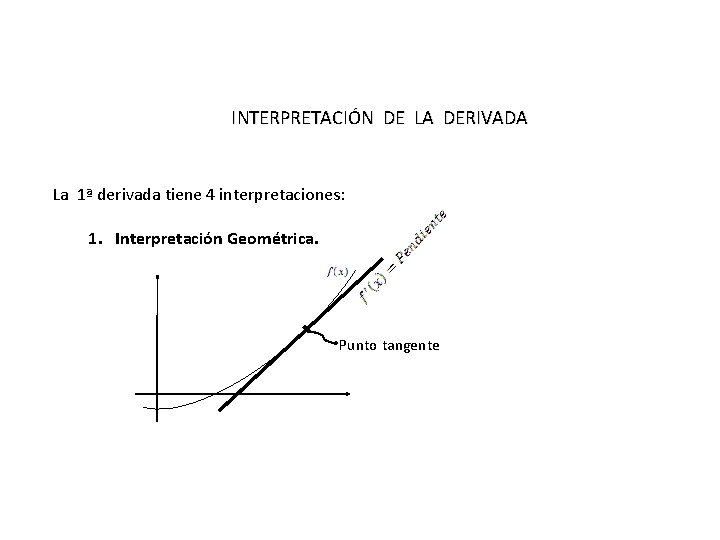
INTERPRETACIÓN DE LA DERIVADA La 1ª derivada tiene 4 interpretaciones: 1. Interpretación Geométrica. Punto tangente

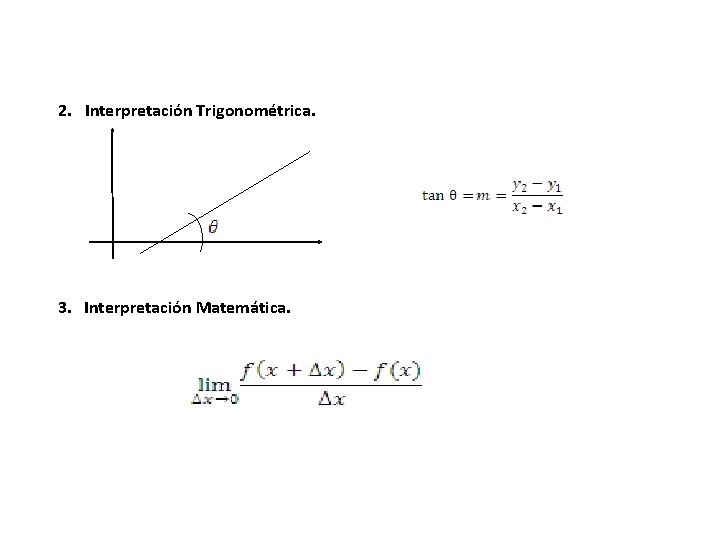
2. Interpretación Trigonométrica. 3. Interpretación Matemática.

4. Interpretación a la Física. Máximos y Mínimos • Criterio de la primera derivada. 1. Se obtiene la función 2. Se obtiene la 1 a derivada. 3. Se iguala a cero la 1ª derivada y se obtiene sus raíces o puntos críticos.

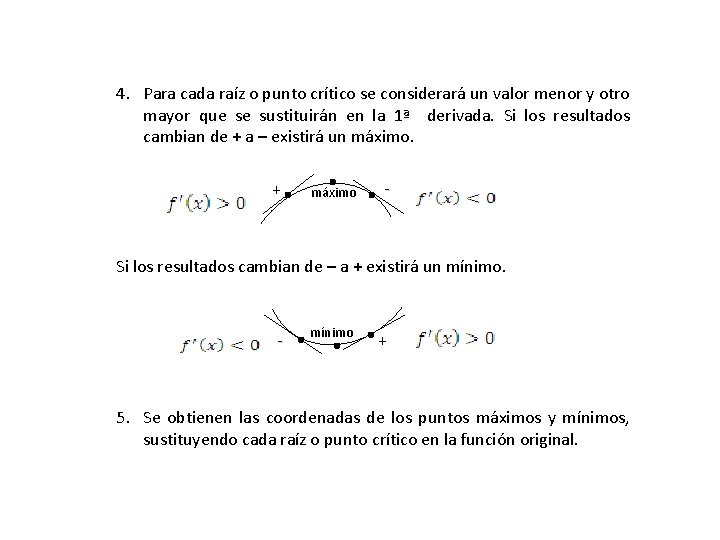
4. Para cada raíz o punto crítico se considerará un valor menor y otro mayor que se sustituirán en la 1ª derivada. Si los resultados cambian de + a – existirá un máximo. + . . . máximo Si los resultados cambian de – a + existirá un mínimo. . - mínimo + 5. Se obtienen las coordenadas de los puntos máximos y mínimos, sustituyendo cada raíz o punto crítico en la función original.

• Criterio de la segunda derivada. 1. Se obtiene la función 2. Se obtiene la 1 a y 2ª derivada. 3. Se iguala a cero la 1ª derivada y se determinan sus raíces o puntos críticos. 4. Cada raíz o punto crítico se sustituye en la 2ª derivada y si el resultado es positivo (+) existirá un mínimo, si el resultado es negativo (-) existirá un máximo y si da cero entonces no existirá ni máximo ni mínimo. máximo . . - mínimo +

Punto de Inflexión • Criterio de la segunda derivada. 1. Se obtiene la función 2. Se obtiene la 1 a y 2ª derivada. 3. Se iguala la 2ª derivada con cero y se determinan las raíces o puntos críticos. 4. Se considerará para cada raíz o punto crítico, un valor menor y otro mayor que se sustituirán en la 2ª derivada, si los resultados cambian de signo de + a - ó – a + se dice que existe un punto de inflexión, si no hay cambio de signo, entonces no existirá un punto de inflexión.

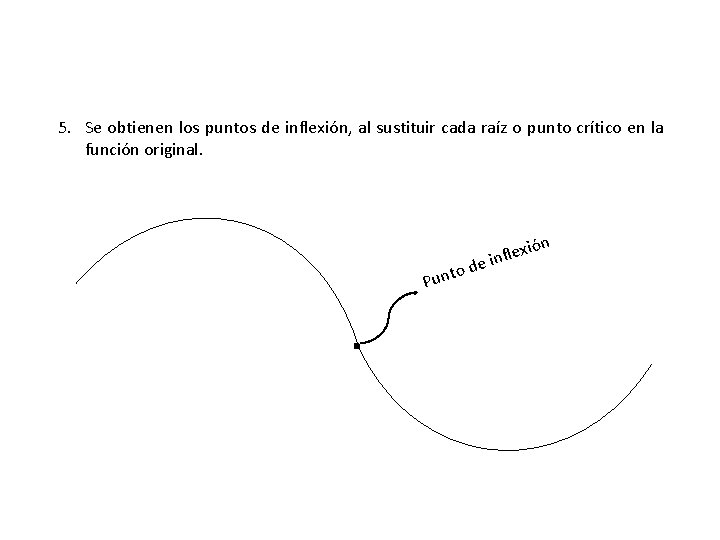
5. Se obtienen los puntos de inflexión, al sustituir cada raíz o punto crítico en la función original. o Punt . d ión x e l f e in

Sentido de la concavidad • Criterio de la segunda derivada. 1. Se obtiene la función 2. Se obtiene la 1 a y 2ª derivada. 3. Se iguala a cero la 2ª derivada y se determinan sus raíces o puntos críticos. 4. Por separado y para cada raíz se considerará un valor menor y un valor mayor, si el resultado es positivo se dice que la función es cóncava y si es negativo se tiene una función convexa o cóncava hacia abajo. (-) (+)

Función Creciente y Decreciente • Criterio de la primera derivada. 1. Se obtiene la función 2. Se obtiene la 1ª derivada. 3. Se iguala a cero la 1ª derivada y se determinan sus raíces o puntos críticos.

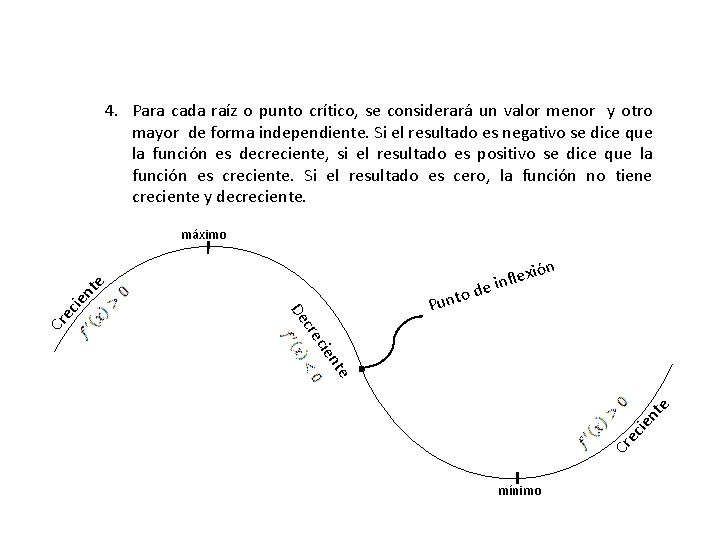
4. Para cada raíz o punto crítico, se considerará un valor menor y otro mayor de forma independiente. Si el resultado es negativo se dice que la función es decreciente, si el resultado es positivo se dice que la función es creciente. Si el resultado es cero, la función no tiene creciente y decreciente. d ien te . ec ec ón lexi f n i e Cr e nt cie cre Cr o Punt De ien te máximo mínimo

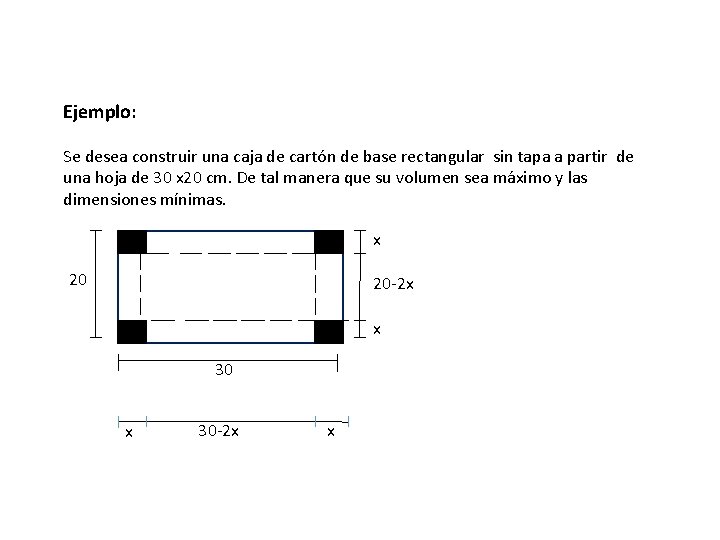
Ejemplo: Se desea construir una caja de cartón de base rectangular sin tapa a partir de una hoja de 30 x 20 cm. De tal manera que su volumen sea máximo y las dimensiones mínimas. x 20 20 -2 x x 30 -2 x x

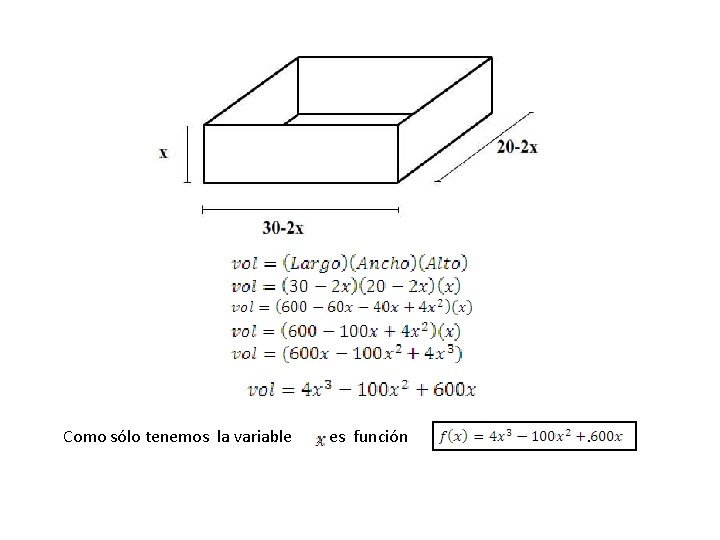
Como sólo tenemos la variable , es función .

• Método ó Criterio de la 1 era derivada para calcular los máximos y mínimos. Paso 1 Se obtiene la función Paso 2 Se determina la 1ª derivada Paso 3 Se iguala a cero y se determinan las raíces ó puntos críticos.

Se resuelve por fórmula general

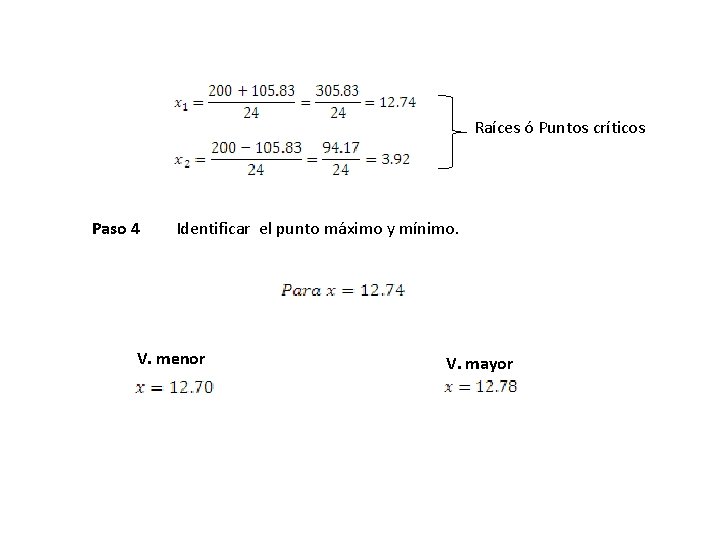
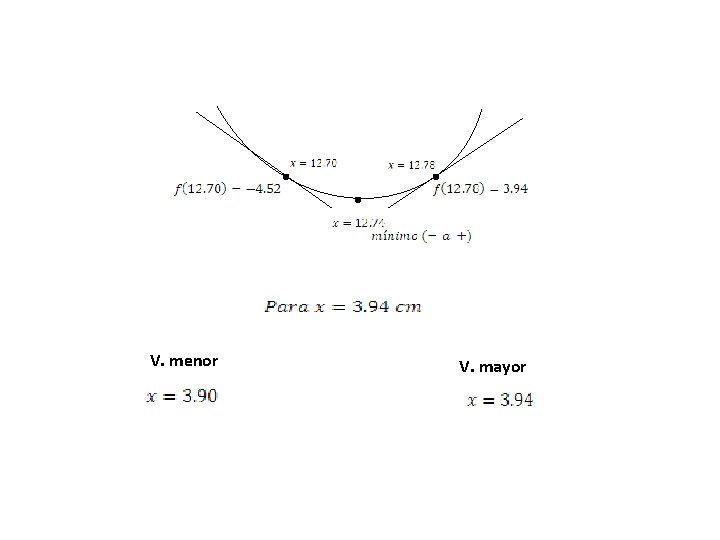
Raíces ó Puntos críticos Paso 4 Identificar el punto máximo y mínimo. V. menor V. mayor

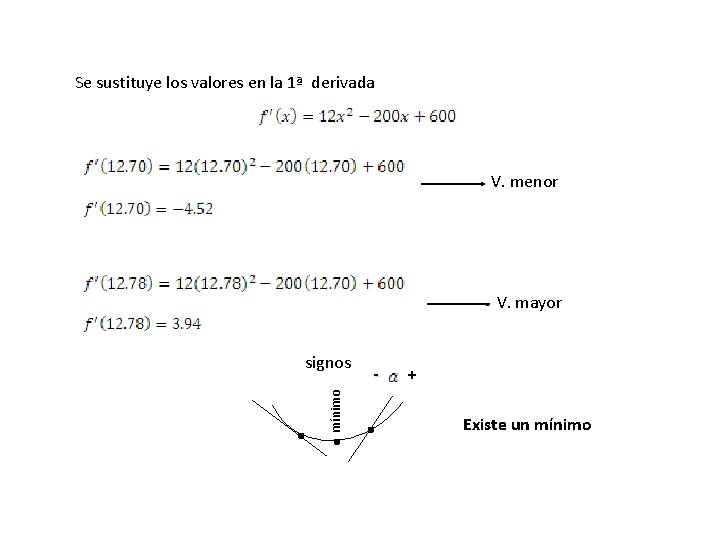
Se sustituye los valores en la 1ª derivada V. menor V. mayor mínimo signos - + Existe un mínimo . . .

. . . V. menor V. mayor

Se sustituye los valores en la 1ª derivada V. menor V. mayor signos + - Existe un máximo

. . . Paso 5 Obtención de las coordenadas. Se obtienen sustituyendo cada raíz o punto crítico en la función original. Para el punto mínimo

Para el punto máximo • Método ó Criterio de la 2ª derivada para calcular los máximos y mínimos. Paso 1 Se obtiene la 1ª derivada Paso 2 Se determinan la 1ª y 2ª derivada

Paso 3 Se iguala a cero la 1ª derivada y se determinan sus raíces ó puntos críticos. Se resuelve por fórmula general

Raíces ó Puntos críticos Paso 4 Se sustituye cada raíz en la 2ª derivada. Mínimo

Máximo Paso 5 Obtención de las coordenadas de los puntos máximos y mínimos, sustituyendo las raíces ó puntos críticos en la función original. Para el punto mínimo

Para el punto máximo • Punto de Inflexión Método de la 2ª derivada Paso 1 Se obtiene la función Paso 2 Se obtiene la 1 a y 2ª derivada.

Paso 3 Se iguala a cero la 2ª derivada y se determinan las raíces o puntos críticos. Paso 4 Para cada raíz o punto crítico, se considerará un valor menor y un valor mayor que se sustituirán en la 2ª derivada. V. menor V. mayor

Se sustituye los valores en la 2ª derivada Signos cambian de – a + Existe punto de Inflexión.

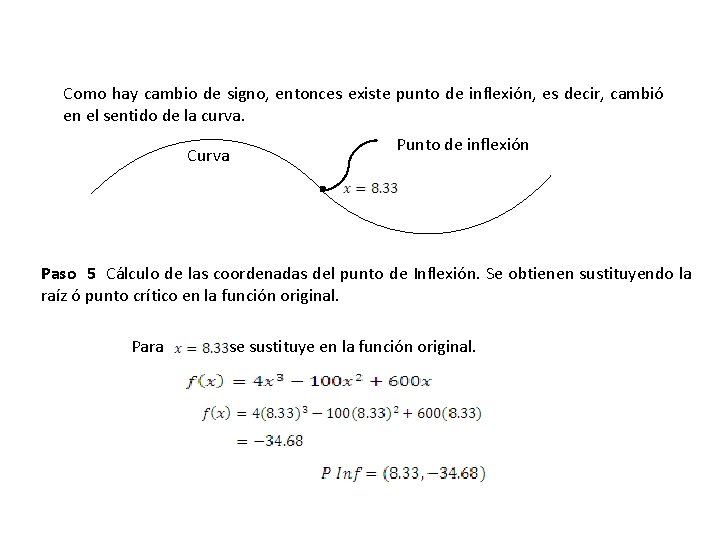
Como hay cambio de signo, entonces existe punto de inflexión, es decir, cambió en el sentido de la curva. Curva . Punto de inflexión Paso 5 Cálculo de las coordenadas del punto de Inflexión. Se obtienen sustituyendo la raíz ó punto crítico en la función original. Para se sustituye en la función original.

• Sentido de la Concavidad Método ó Criterio de la 2ª derivada Paso 1 Se obtiene la función Paso 2 Se obtiene la 1 a y 2ª derivada. Paso 3 Se iguala a cero la 2ª derivada y se determinan sus raíces o puntos críticos. Raíz ó Punto Crítico

Paso 4 Para cada raíz o punto crítico, se considerará un valor mayor y otro menor de manera independiente. V. menor V. mayor Se sustituye los valores en la 2ª derivada Función Convexa Función Cóncava

• Función Creciente y Decreciente Paso 1 Se obtiene la función Paso 2 Se determina la 1ª derivada Paso 3 Se iguala a cero y se determinan las raíces ó puntos críticos.

Se resuelve por fórmula general

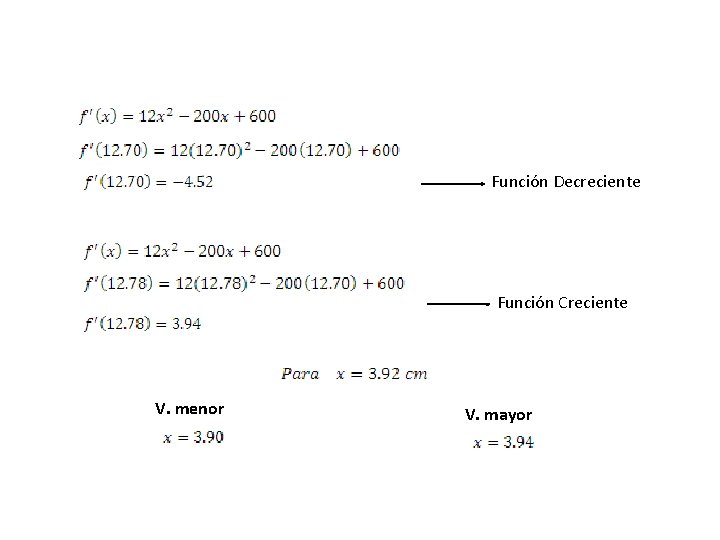
Raíces ó Puntos críticos Paso 4 Para cada raíz ó punto crítico de manera independiente, se considerará un valor menor y otro mayor que se sustituirán en la 1ª derivada. V. menor V. mayor

Función Decreciente Función Creciente V. menor V. mayor

Función Creciente Función Decreciente Resultados Punto Máximo Pmax=(3. 92, 1056. 31) Punto Mínimo Pmin=(12. 74, -315. 56) Punto Inflexión PInf=(8. 33, -34. 68)

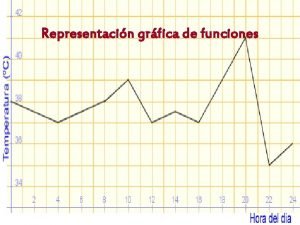
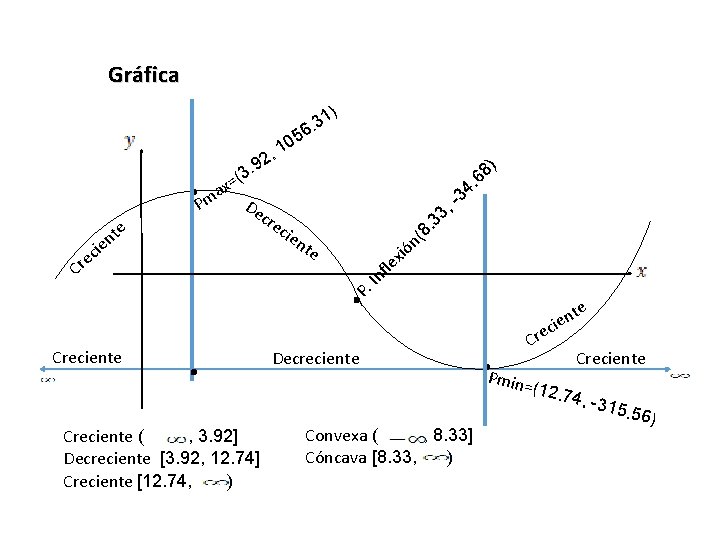
Gráfica 5 . Pmax De Creciente ) 8 6 cre cie nt e ec Cr ) 2 . 9 3 ( = te n ie 0 , 1 1 3. 6 . P. . Creciente ( , 3. 92] Decreciente [3. 92, 12. 74] Creciente [12. 74, ) - n xió fle n I 3, 3. (8 . 4 3 Decreciente Convexa ( , 8. 33] Cóncava [8. 33, ) te en i c e Cr . Pmin= (12. 7 Creciente 4, -3 15. 56 )

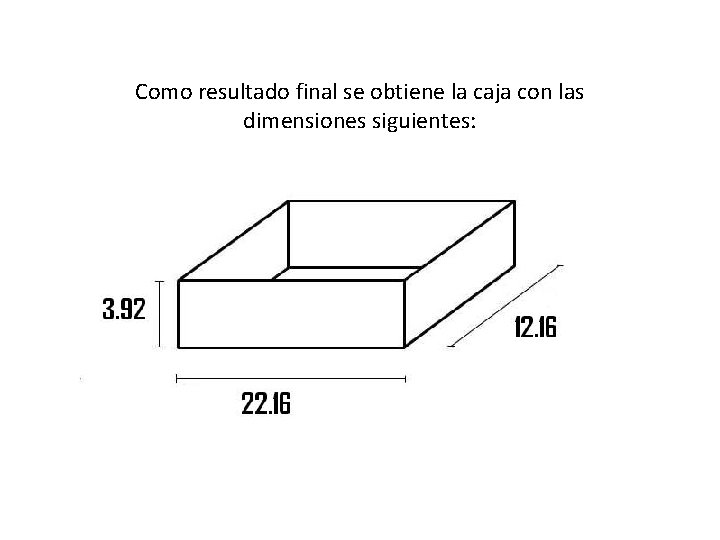
Como resultado final se obtiene la caja con las dimensiones siguientes: