Ensino Superior Clculo 3 5 Derivadas Direcionais Gradientes

Ensino Superior Cálculo 3 5. Derivadas Direcionais, Gradientes e Pontos Críticos Amintas Paiva Afonso

Derivadas Direcionais As derivadas parciais de uma função de duas variáveis f(x, y) são consideradas na direção do eixo x (fx) ou do eixo y (fy). Quando se considera uma direção qualquer no domínio de f(x, y), ou seja, no plano xy, têm-se a derivada direcional que vale: Foi considerada a direção do vetor unitário u, u = cosqi + senqj

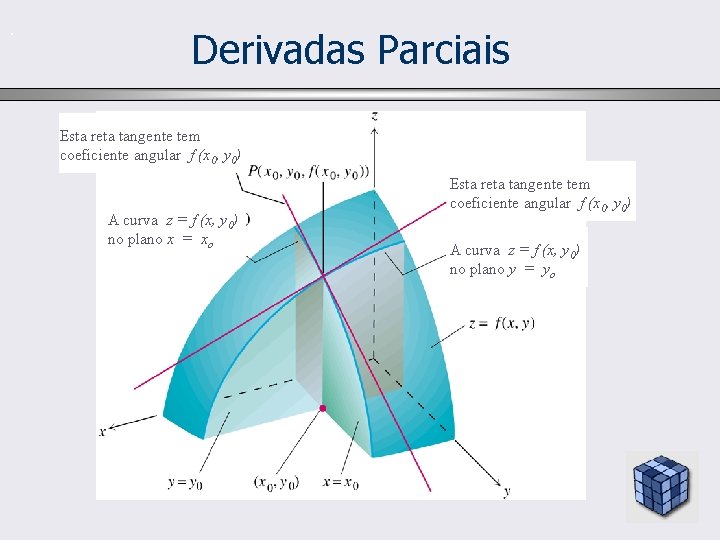
. Derivadas Parciais Esta reta tangente tem coeficiente angular f (x 0, y 0) A curva z = f (x, y 0) no plano x = xo Esta reta tangente tem coeficiente angular f (x 0, y 0) A curva z = f (x, y 0) no plano y = yo

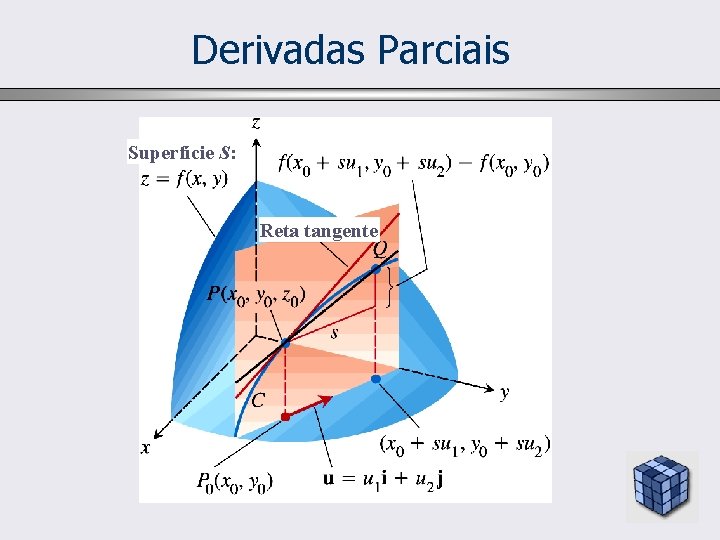
Derivadas Parciais Superfície S: Reta tangente

Gradiente de uma função de várias variáveis O segundo termo do produto escalar da derivada direcional é o vetor gradiente. Este vetor fornece a direção e sentido no qual ocorre a maio variação das curvas de níveis da função de duas variáveis.

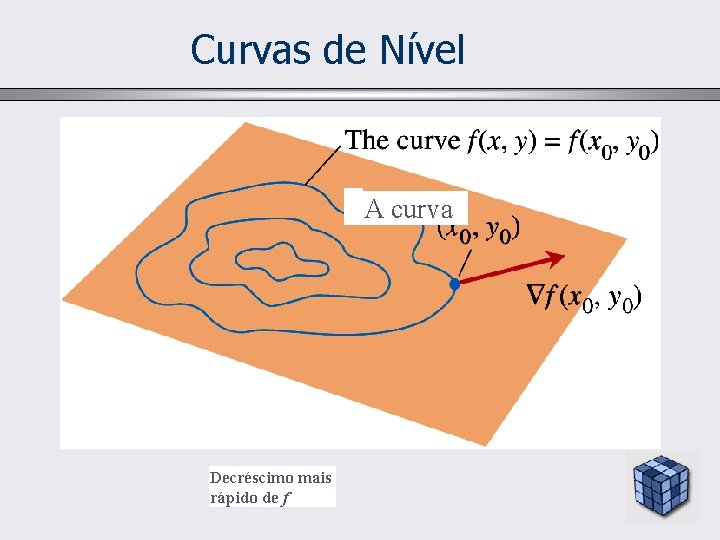
Decréscimo mais rápido de f Aumento mais rápido de f Variação zero de f

Curvas de Nível A curva Decréscimo mais rápido de f

Exercícios 1) Se f(x, y) = 5 x 2 + 3 y, ache o gradiente e o valor da função no ponto (1, 2). Ache tb a taxa de variação de f(x, y) na direção de 0, 25 p neste ponto. 2) A temperatura em cada ponto (x, y) de uma placa retangular situada no plano xy é determinada pela expressão: T(x, y) = x 2 + y 2. (a) Ache a taxa de variação da temperatura no ponto (3, 4) na direção e no sentido que fazem um ângulo de 0, 33 p com o eixo x positivo. (b) ache a direção e o sentido em que a taxa de variação no ponto (-3, 1) é máxima.

Pontos Críticos Máximo e Mínimo Local: a) f(a, b) é um valor máximo local de f(x, y), se f(a, b) > f(x, y) para todos os pontos do domínio (x, y) em um disco aberto centrado em (a, b). b) f(a, b) é um valor mínimo local de f(x, y), se f(a, b) < f(x, y) para todos os pontos do domínio (x, y) em um disco aberto centrado em (a, b). Nestes dois casos fx = fy = 0

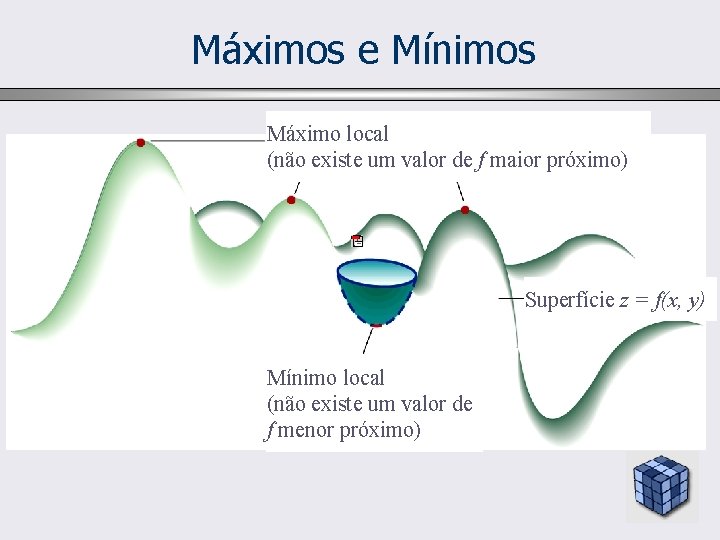
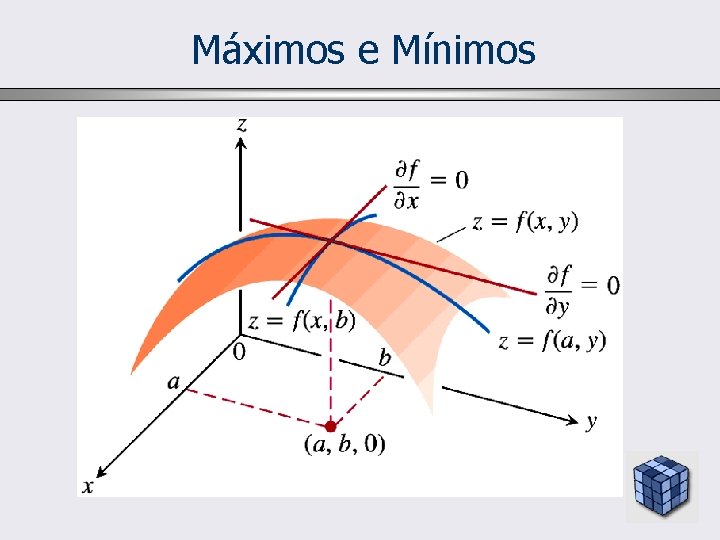
Máximos e Mínimos Máximo local (não existe um valor de f maior próximo) Superfície z = f(x, y) Mínimo local (não existe um valor de f menor próximo)

Máximos e Mínimos

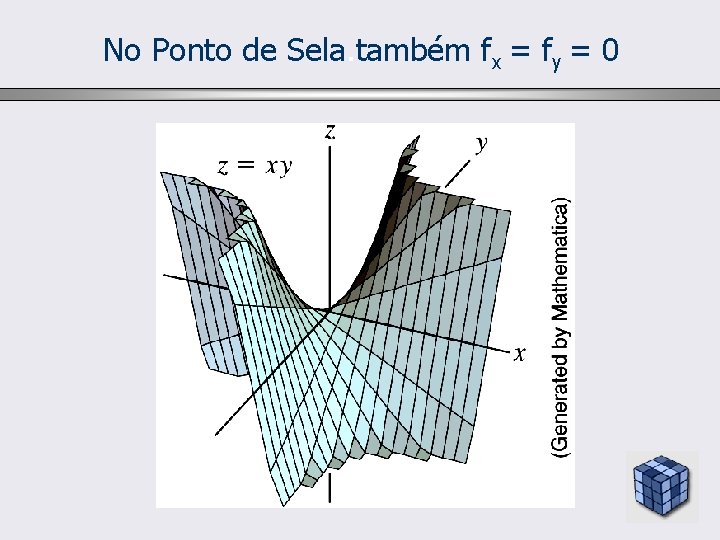
No Ponto de Sela. também fx = fy = 0

Pontos Críticos de f(x, y) Critérios: (a) Máximo: fxxfyy – (fxy)2 > 0 e fxx < 0 (b) Mínimo: fxxfyy – (fxy)2 > 0 e fxx > 0 (c) Ponto de sela: fxxfyy – (fxy)2 < 0 (d) Teste inconclusivo: fxxfyy – (fxy)2 = 0

Exercícios 1) Encontrar os valores extremos locais da função f(x, y) = xy - x 2 - y 2 - 2 x - 2 y+ 4. 2) Encontrar os valores extremos locais da função f(x, y) = xy.