Ensino Superior Clculo 3 8 Integrais Duplas Momentos

Ensino Superior Cálculo 3 8. Integrais Duplas Momentos e Centro de Gravidade Amintas Paiva Afonso

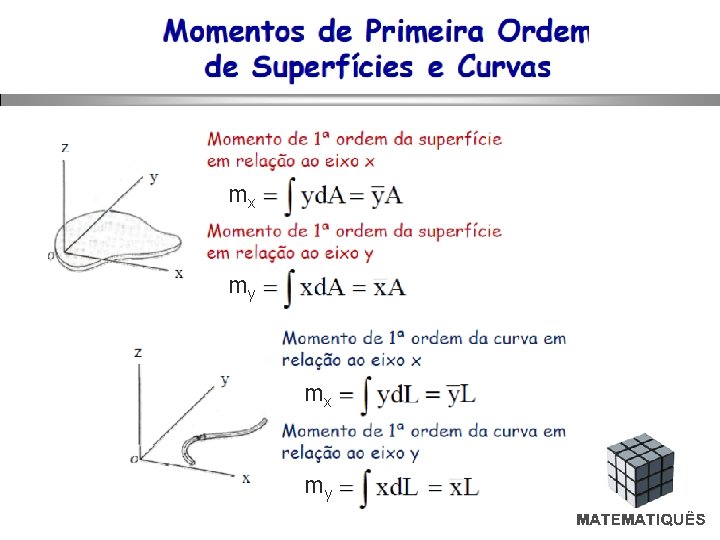
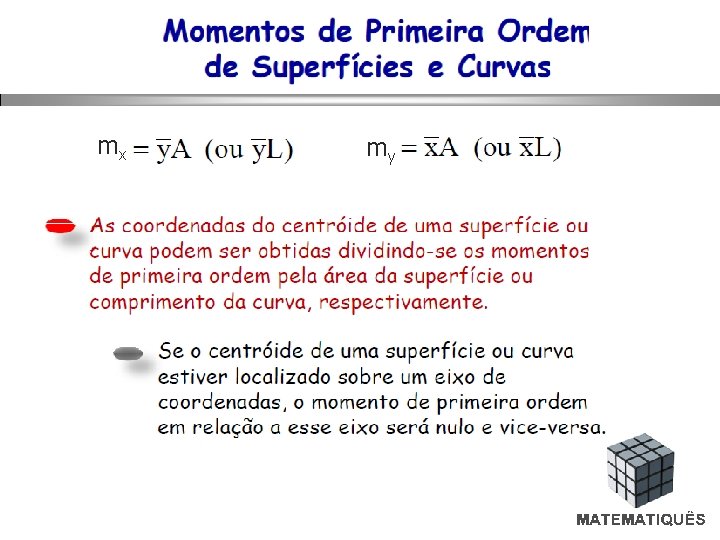
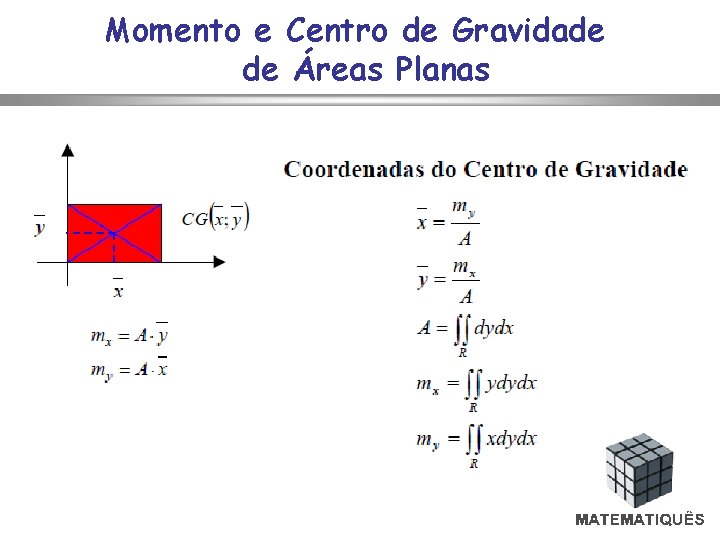
Momentos de primeira ordem ou Momentos Estáticos As integrais pertinentes ao cálculo das coordenadas do Centróide recebem o nome de Momentos de Primeira Ordem em relação aos eixos y e x, respectivamente, cuja notação é expressa por: mx my Cabe ressaltar que tais integrais podem ser entendidas, por analogia aos momentos dos pesos, como momentos das áreas em relação aos eixos coordenados, motivo pelo qual são denominadas Momentos Estáticos.

mx my

mx my

mx my

mx

my

mx

my

mx

my

Aplicações

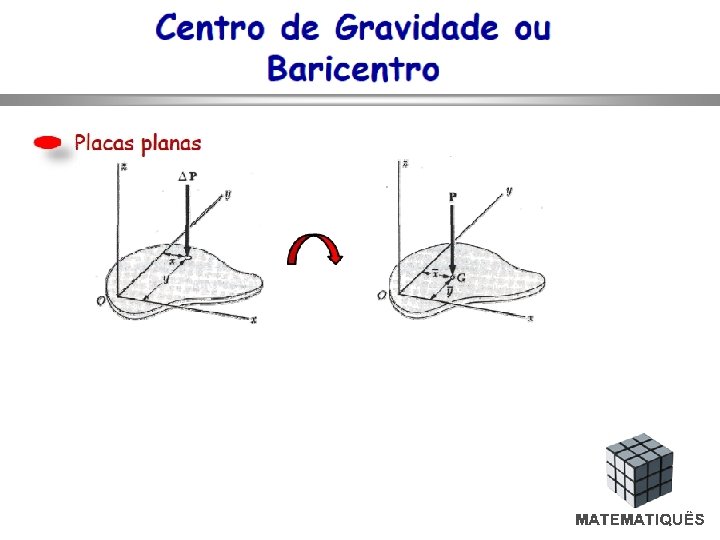
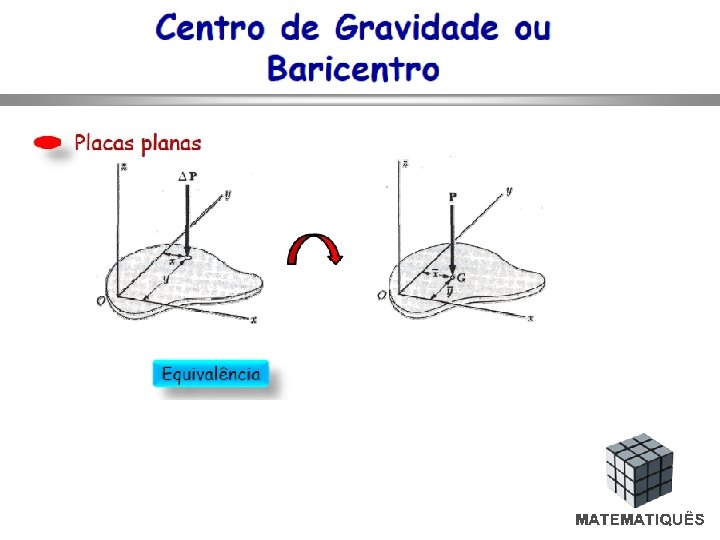
Baricentros e centróides Superfície de espessura constante Peso total P, dividida em n elementos , de pesos individuais ΔP O peso total P da superfície, conforme se sabe, é dado por: sendo que, no limite:

Baricentros e centróides Para determinar as coordenadas do ponto de aplicação da resultante P, denominado Baricentro ou Centro de Gravidade da superfície, basta escrever somatórios de momentos dos pesos em relação aos eixos , ou sejam: Levando tais expressões ao limite, tem-se: Analogamente às considerações feitas para o Peso P, tem-se: onde as coordenadas , denominadas Centróide ou Centro Geométrico da superfície A, neste caso particular, coincidem com as do Baricentro.

Momento e Centro de Gravidade de Áreas Planas

Exercícios 1) Determinar as coordenadas do centro de gravidade da Região limitada no 1º Quadrante por y = x 3 e y = 4 x. Resposta:

Exercícios 2) Determinar as coordenadas do centro de gravidade da Região limitada no 1º Quadrante por y 2 = x, x + y = 2 e y = 0. Resposta:

Momentos de segunda ordem ou Momentos de Inércia De modo análogo aos Momentos de Primeira Ordem, cujas expressões contêm funções x e y, as integrais do tipo abaixo são denominadas Momentos de Segunda Ordem ou Momentos Inércia em relação aos eixos x e y respectivamente, em notação dada por:

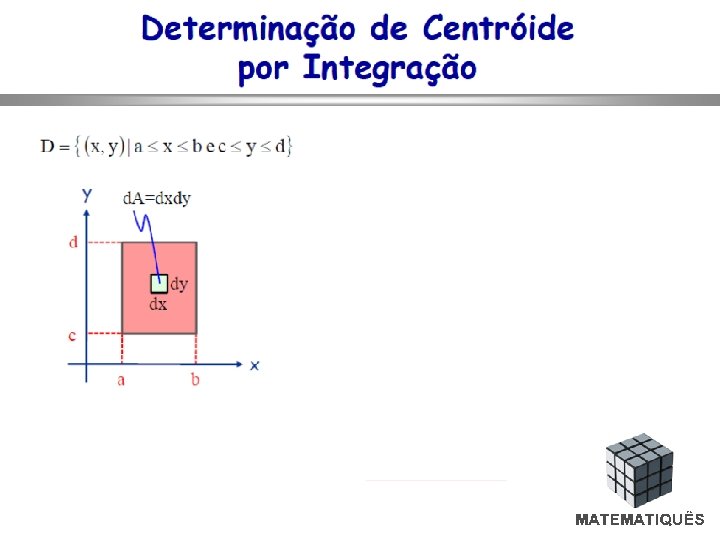
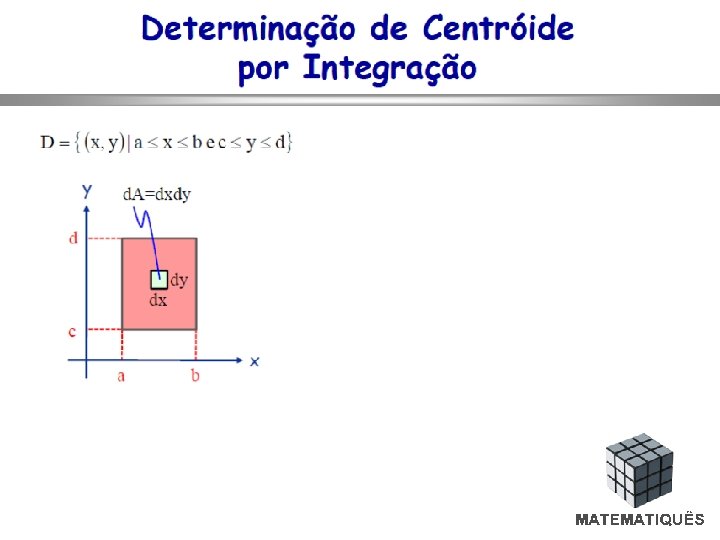
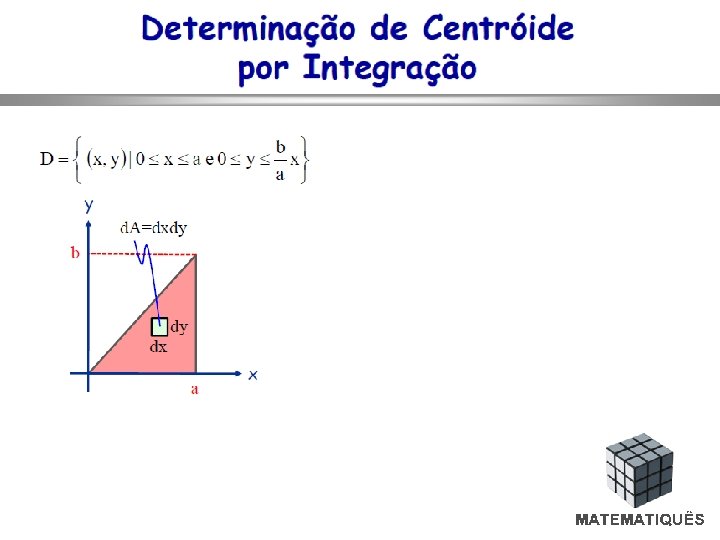
FÓRMULA PARA CÁLCULO DE INTEGRAL DUPLA Nestas integrais, a exemplo do cálculo de áreas, nota-se que é um problema de integração dupla. Para calculá-las, basta ter em conta a definição de integral dupla de uma função qualquer no domínio A localizado entre duas curvas, conforme mostra a figura seguinte:

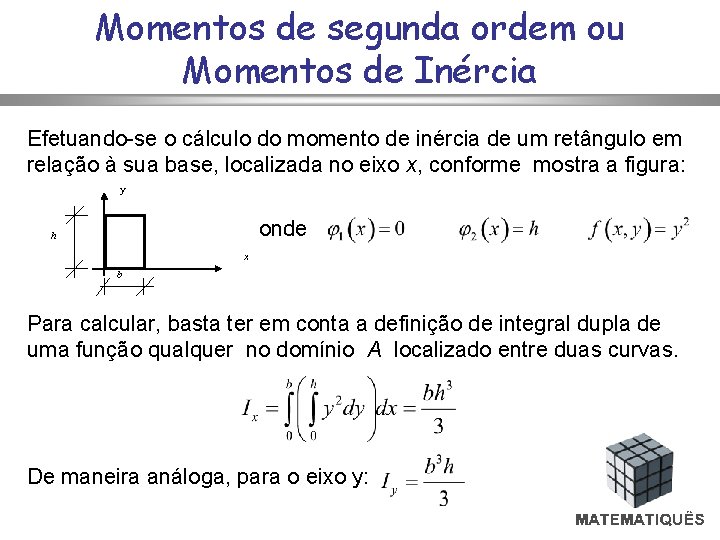
Momentos de segunda ordem ou Momentos de Inércia Efetuando-se o cálculo do momento de inércia de um retângulo em relação à sua base, localizada no eixo x, conforme mostra a figura: y onde h Para calcular, basta ter em conta a definição de integral dupla de uma função qualquer no domínio A localizado entre duas curvas. x b De maneira análoga, para o eixo y:

Cálculo dos Momentos de Inércia Fazemos o cálculo dos momentos de inércia mediante a integral: Para um objeto tridimensional é conveniente utilizar a densidade do volume: Então:

Teorema dos Eixos Paralelos O teorema dos eixos paralelos estabelece que o momento de inércia ao redor de qualquer eixo que é paralelo e que se encontra a uma distância D do eixo que passa pelo centro de massa é I = ICM + MD 2

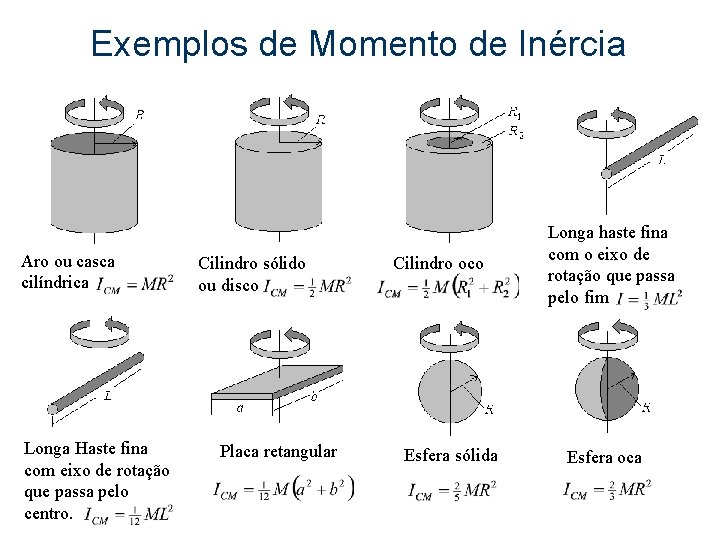
Exemplos de Momento de Inércia Aro ou casca cilíndrica Longa Haste fina com eixo de rotação que passa pelo centro. Cilindro sólido ou disco Placa retangular Cilindro oco Esfera sólida Longa haste fina com o eixo de rotação que passa pelo fim Esfera oca

Cálculo dos Momento de Inércia

Exercício 1 Determinar os momentos de inércia Ix ; Iy e I 0 da região limitada pelas curvas y 2 = 4 x; x = 4 e y = 0, no 1º Quadrante. Resposta: 107, 28

Exercício 2 Determinar os momentos de inércia Ix ; Iy e I 0 da região limitada pelas curvas y 2 = 4 x; x + y = 3 e y = 0, no 1º Quadrante. Resposta: 8, 97