Ensino Superior Clculo 3 9 Integrais Duplas Volumes

Ensino Superior Cálculo 3 9. Integrais Duplas Volumes Amintas Paiva Afonso

Integrais Duplas - Volume • Na tentativa de resolver o problema de determinar áreas, chegamos à definição de integral definida. Vamos aplicar procedimento semelhante para calcular o volume de um sólido e, no processo, chegar à definição de integral dupla.

f : IR 2 IR contínua no retângulo R = [a, b] x [c, d] y • Consideremos uma função f de duas variáveis definida em um retângulo fechado d R = [a, b] x [c, d] = { (x, y) IR 2| a < x < b, c < y < d } R c a b x

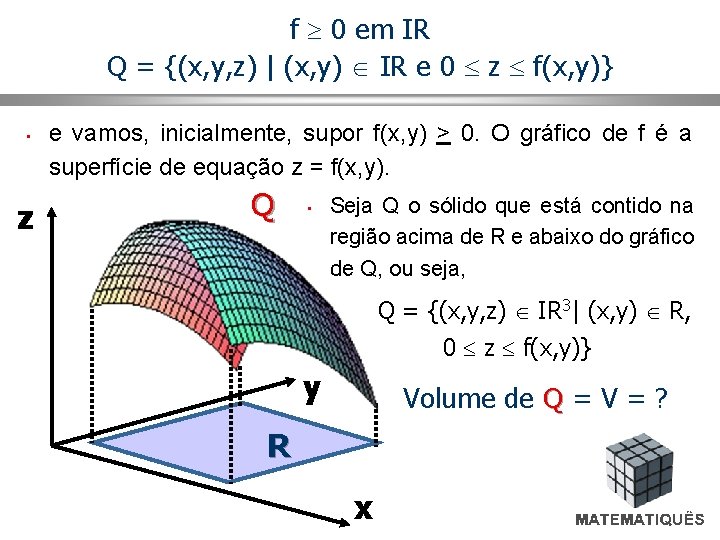
f 0 em IR Q = {(x, y, z) | (x, y) IR e 0 z f(x, y)} • z e vamos, inicialmente, supor f(x, y) > 0. O gráfico de f é a superfície de equação z = f(x, y). Q • Seja Q o sólido que está contido na região acima de R e abaixo do gráfico de Q, ou seja, Q = {(x, y, z) IR 3| (x, y) R, n 0 z f(x, y)} y Volume de Q = V = ? R x

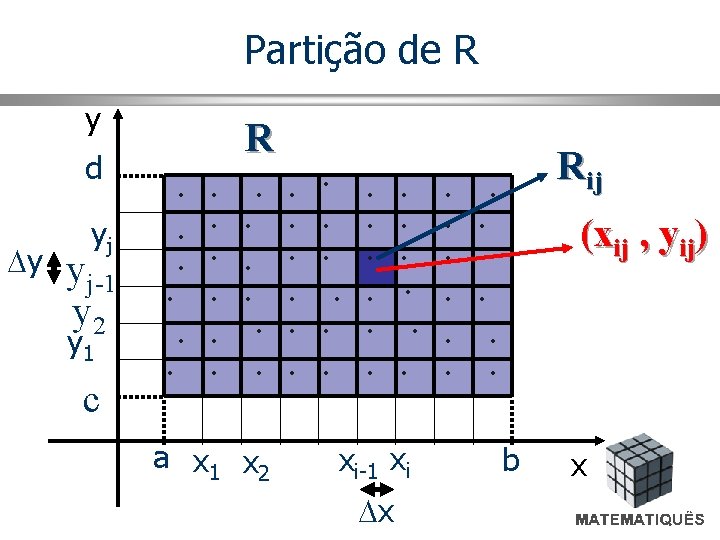
Partição de R • O primeiro passo consiste em dividir o retângulo R em subretângulos. Faremos isso dividindo o intervalo [a, b] em m subintervalos [xi-1 , xi], de mesmo comprimento x = (b – a) / m, e o intervalo [c, d] em n subintervalos [yj-1 , yj], de mesmo comprimento y = (b – a) / n. traçando retas paralelas aos eixos coordenados passando pelos extremos dos subintervalos, formamos os sub-retângulos. Rij = [xi-1, xi] x [yj-1, yj ] = {(x, y) | xi-1 < xi , yj-1 < yj } cada um dos quais com área A = x y.

Partição de R y R d y yj yj-1 y 2 y 1 c a x 1 x 2 xi-1 xi x Rij (xij , yij) b x

Integrais Duplas - Volume • Se escolhermos um ponto arbitrário (xij, yij) em cada Rij, podemos aproximar a parte de Q que está acima de cada Rij por uma caixa retangular fina (ou um prisma) com base Rij e altura f(xij, yij). O volume desta caixa é dado pela sua altura vezes a área do retângulo da base: . Vij = f(xij, yij) A.

Integrais Duplas - Volume Se seguirmos com esse procedimento para todos os retângulos e somarmos os volumes das caixas correspondentes, obteremos uma aproximação do volume total de Q: Essa dupla soma significa que, para cada sub-retângulo, calculamos o valor de f no ponto amostra escolhido, multiplicamos esse valor pela área do sub-retângulo e, então, adicionamos os resultados.

Integrais Duplas - Volume z Q f (xij , yij) Vij y R V= (xij , yij) x

Integrais Duplas - Volume

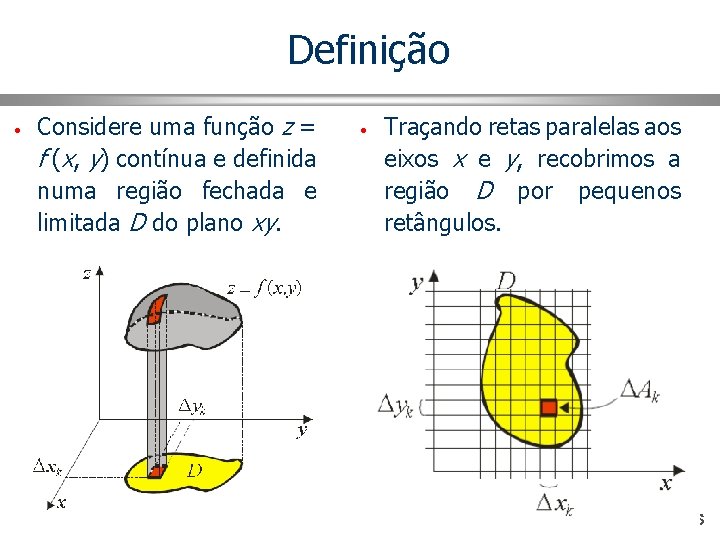
Definição • Considere uma função z = f (x, y) contínua e definida numa região fechada e limitada D do plano xy. • Traçando retas paralelas aos eixos x e y, recobrimos a região D por pequenos retângulos.

Definição • Considere somente os retângulos Rk que estão totalmente contidos em D, numerando-os de 1 a n. Em cada retângulo Rk, tome o ponto Pk = (xk , yk) e forme a soma • SOMA DE RIEMANN: onde Ak = xk. yk é a área do retângulo Rk. • Traçando-se mais retas paralelas aos eixos x e y, os retângulos ficam cada vez menores. Toma-se mais retas tal que a diagonal máxima dos retângulos Rk tende a zero quando n tende ao infinito.

Definição • Então, se existe, ele é chamado INTEGRAL DUPLA de f (xk , yk) Ak sobre a região D. Denota-se por:

Interpretação Geométrica • • Se f (x, y) 0, f (xk , yk) Ak representa o volume de um prisma reto, cuja base é o retângulo Rk e cuja altura é f (xk , yk). A soma de Riemann é a aproximação do volume limitado abaixo da região z e acima de D.

Interpretação Geométrica • Assim, se z = f (x, y) 0, então é o VOLUME DO SÓLIDO delimitado superiormente pelo gráfico de z = f (x, y) e inferiormente pela região D.

Interpretação Geométrica Área da Região D Se f(x, y) = 1 P(x, y) D, então, V = 1. área. D. Logo:

Cálculo de Volumes - Aplicações A Integral dupla dá o volume sob a superfície f(x, y)

Cálculo de Volumes - Aplicações Para f (x, y) 0, a integral nos dá o volume do sólido delimitado superiormente pelo gráfico de z = f (x, y), inferiormente pela região D e lateralmente pelo cilindro vertical cuja base é o contorno de D.

Exemplos Calcular o volume do sólido delimitado superiormente pelo gráfico de z = 4 - x - y inferiormente pela região delimitada por x = 0, x = 2, y = 0 e e lateralmente pelo cilindro vertical cuja base é o contorno de R. Resposta: V = 15/4 u. v. n. Representamos na Figura a região R (base deste sólido): n. Assim, 0 x 2 e , logo a região é do Tipo I e podemos integrar deste modo:

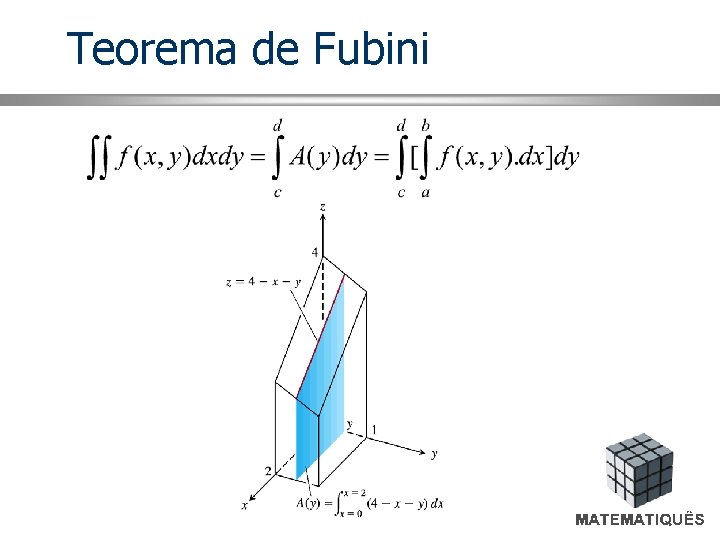
Teorema de Fubini

Teorema de Fubini

Exercícios 1) Determinar o volume do sólido limitado pelos planos coordenados pelo plano x + y + z = 3, no 1º octante. 3 3

Exercícios 2) Determinar o volume do sólido limitado por z = 4 − x 2 ; x = 0; y = 6; z = 0; y = 0. Resposta: 32 u. v

Exercícios 3) Determinar o volume do sólido limitado no 1º octante pelos cilindros x 2 + y 2 = a 2 e x 2 + z 2 = a 2. a a a Resposta: 2 a 3/3 u. v.

Exercícios 4) Determinar o volume do sólido limitado superiormente por z = 2 x + y + 4 e inferiormente por z = − x − y + 2 e lateralmente pela superfície definida pelo contorno da região D limitada pelas curvas y = x 2 – 4 e

Exercícios Resposta: -22/15 u. v.

Exercícios 5) Determine o volume do sólido S que é delimitado pelo parabolóide elíptico x 2 + 2 y 2 + z = 16, os planos x = 2 e y = 2 e os três planos coordenados. Primeiro, observamos que S é o sólido que se encontra sob a superfície e acima de Resposta: 48

Exercícios 6)Determine o volume do sólido que está abaixo do parabolóide z = x 2 + y 2 e acima da região do plano xy limitada pela reta y = 2 x e pela parábola y = x 2. y = 2 x y = x 2 Resposta: 216/35

Exercícios 8) Determine o volume do tetraedro limitado pelos planos x + 2 y + z = 2, x = 2 y, x = 0 e z = 0.

Exercícios 8) Determine o volume do tetraedro limitado pelos planos x + 2 y + z = 2, x = 2 y, x = 0 e z = 0. Resposta: 1/3

Exercícios