Ensino Superior Clculo 3 9 Integrais Duplas Coordenadas

Ensino Superior Cálculo 3 9. Integrais Duplas Coordenadas Polares Amintas Paiva Afonso

Mudança de Variáveis em Integrais Duplas Através de uma mudança de variáveis x = x(u, v) e y = y(u, v) uma integral dupla sobre uma região D do plano xy pode ser transformada numa integral dupla sobre uma região D ’ do plano uv.

Mudança de Variáveis em Integrais Duplas A correspondência entre as regiões D’ e D é BIJETORA, e podemos retornar de D para D’ através da transformação inversa u = u(x, y) e v = v(x, y). Considerando que as funções em (1) e (2) são contínuas, com derivadas parciais contínuas em D ’ e D, respectivamente, temos (3)

Mudança de Variáveis em Integrais Duplas Onde é o determinante jacobiano de x e y em relação a u e v, dado por

Mudança de Variáveis em Integrais Duplas A transformação que leva pontos (r, ) do plano r a pontos (x, y) do plano xy é dada por (4) e seu jacobiano é dado por Portanto, a fórmula (3) pode ser expressa por: (5)

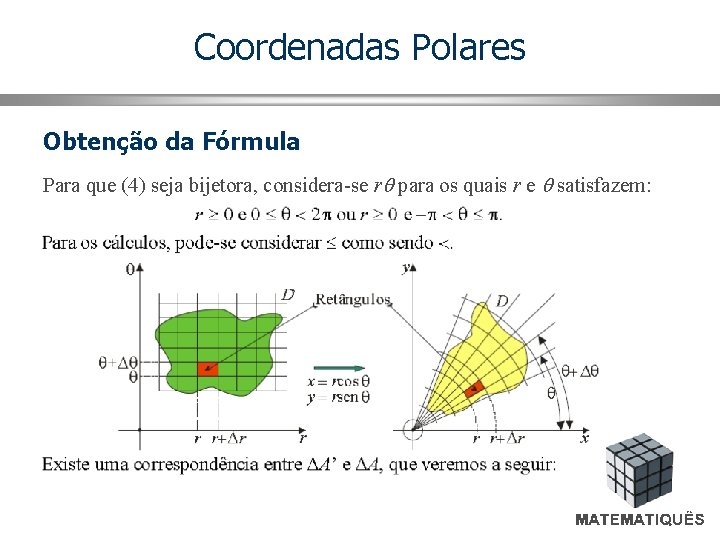
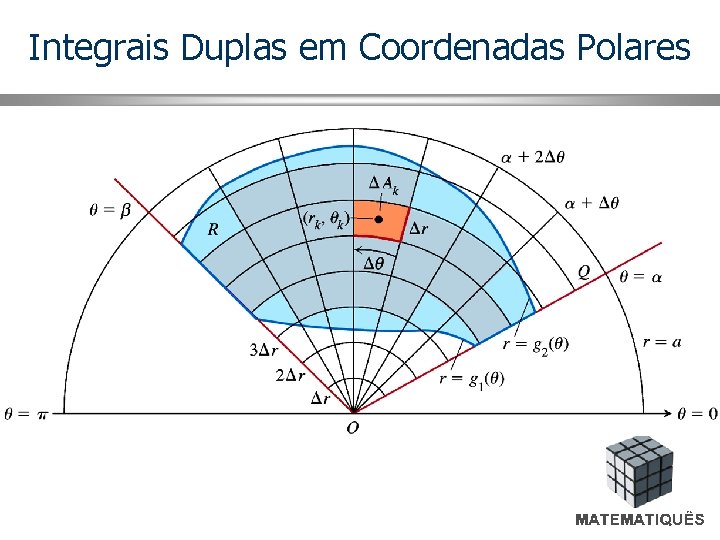
Coordenadas Polares Obtenção da Fórmula Para que (4) seja bijetora, considera-se r para os quais r e satisfazem:

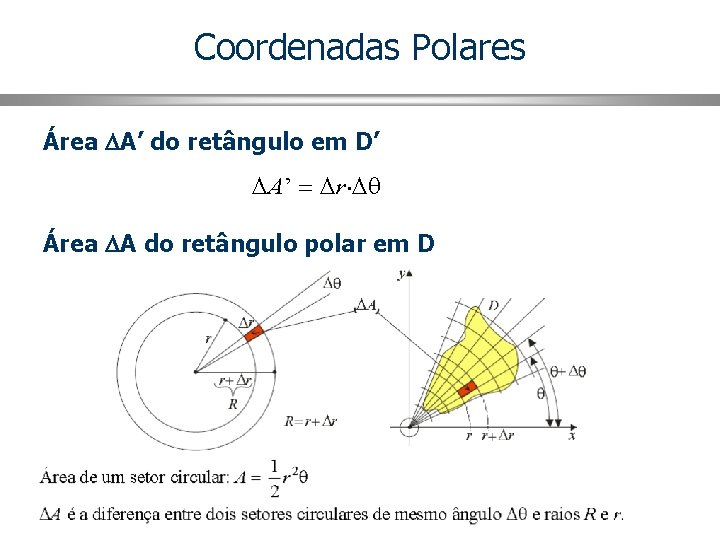
Coordenadas Polares Área A’ do retângulo em D’ Área A do retângulo polar em D

Coordenadas Polares

Coordenadas Polares

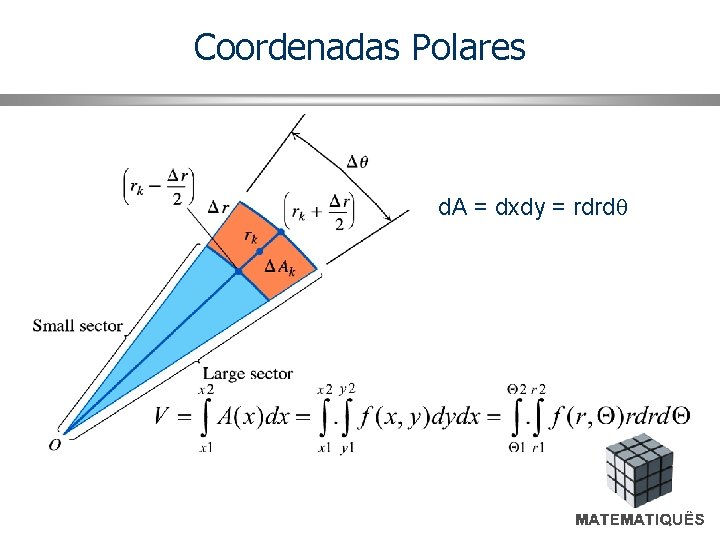
Coordenadas Polares d. A = dxdy = rdrd

Coordenadas Polares Integral Dupla em D’ Assim, obtemos o jacobiano rk da fórmula (5). Enumerando os retângulos polares e 1 a n, tome um ponto arbitrário (xk , yk) no k-ésimo retângulo. Este ponto pode ser representado por (rk cos k , rk sin k) que tem representação (rk , k) referente à região correspondente em D’. Assim, a soma de Riemann é equivalente a onde A'k = rk k é a área do k-ésimo retângulo em D’.

Coordenadas Polares Assim, se tomarmos limite com n com o máximo das diagonais dos n retângulos tendendo a zero, temos que equivale a integral dada pela fórmula (5).

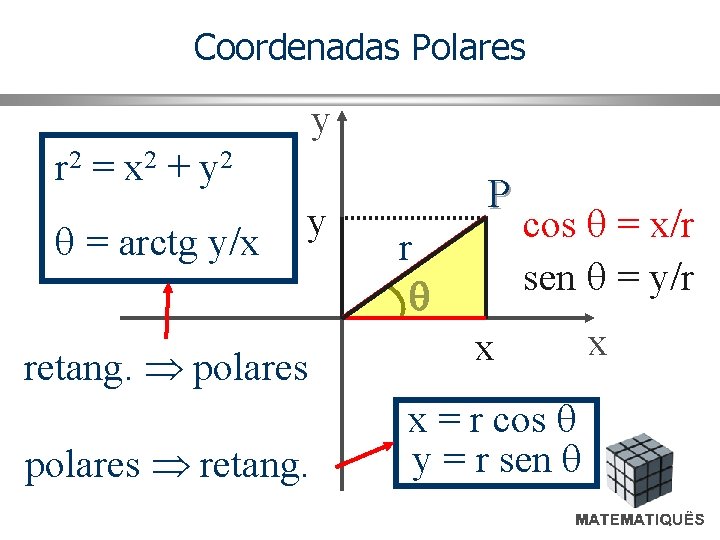
Coordenadas Polares y P(x, y) = P(r, ) y r x x Relações: r 2 = x 2 + y 2 = arctg(y/x) x = r. cos y = r. sen z=z

Coordenadas Polares

Coordenadas Polares y r 2 = x 2 + y 2 = arctg y/x y retang. polares retang. P r cos = x/r sen = y/r x x = r cos y = r sen x

Curvas em Coordenadas Polares y 2 r r = f ( ) 1 2 1 P x

Regiões em Coordenadas Polares y R 2 f 1 ( ) r f 2 ( ) 1 2 1 r = f 1 ( ) r = f 2 ( ) x

Integrais Duplas em Coordenadas Polares y R Rk = (r 12 - r 22)( - )/2 = [(r 1 + r 2)/2] ( r ) r 2 Rk r 1 unidade de área: Rk x

Integrais Duplas em Coordenadas Polares

Cálculo de Integrais Duplas em Coordenadas Polares R: r 1 ( ) r r 2 ( )

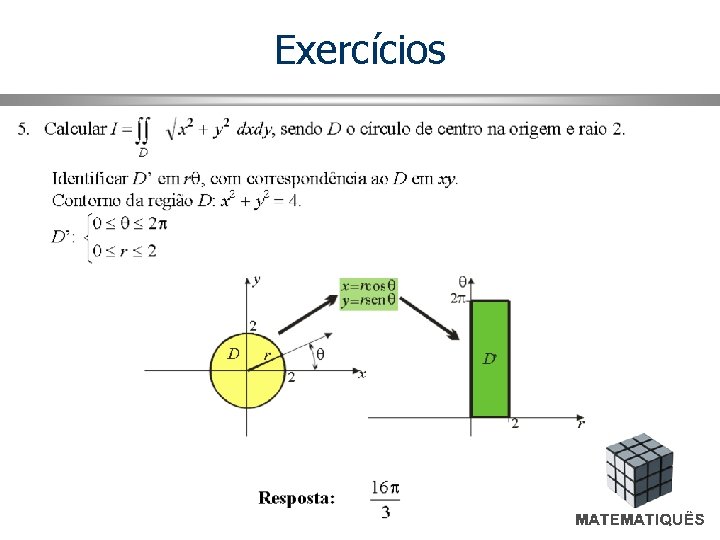
Exercícios Exemplo: Calcular R é a região semicircular, x 2 + y 2 = 1, onde y é positivo. R=1

Área de uma superfície Exemplo: Achar a área do parabolóide z = f(x, y) = x 2 + y 2 abaixo do plano z = 4. (sugestão: usar coordenadas polares).

Exercícios

Exercícios

Cálculo de Volumes - Aplicações Para f (x, y) 0, a integral nos dá o volume do sólido delimitado superiormente pelo gráfico de z = f (x, y), inferiormente pela região D e lateralmente pelo cilindro vertical cuja base é o contorno de D.

Cálculo de Volumes - Aplicações A Integral dupla dá o volume sob a superfície f(x, y)

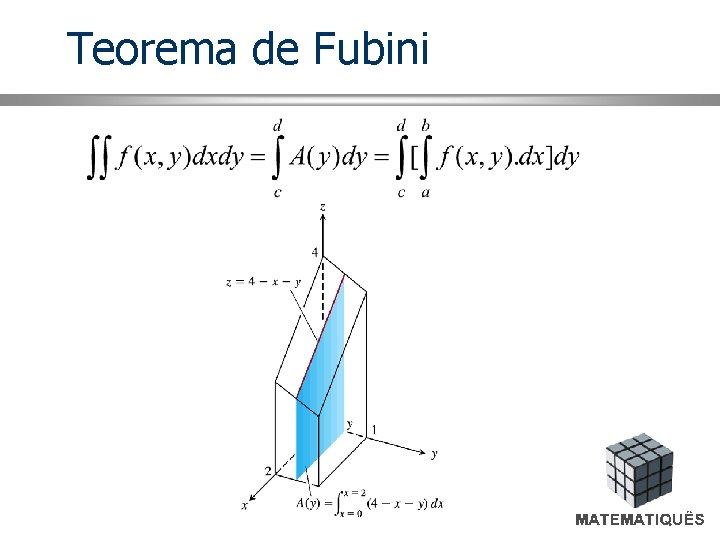
Teorema de Fubini

Teorema de Fubini

Exercícios

Cálculo Áreas de Regiões Planas Fazendo f (x, y) = 1, a área da região de integração D é dada por:

Exercícios