Captulo 5 CONEXES COM A MATEMTICA Funo modular

Capítulo 5 CONEXÕES COM A MATEMÁTICA Função modular ANOTAÇÕES EM AULA Capítulo 5 – Função modular

Módulo ou valor absoluto de um número real Módulo ou valor absoluto, de um número real x, indicado por | x|, é definido como: |x| = x, se x ≥ 0 e | x| = – x, se x < 0 Exemplos a) |4| = 4 c) |0| = 0 e) |– 4| = 4 b) |0, 25| = 0, 25 d) f) CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 1

Módulo ou valor absoluto de um número real a)|– |= (distância do ponto associado a – até a origem) b)| | = (distância do ponto associado a até a origem) c)|– 2| = 2 (distância do ponto associado a – 2 até a origem) d)|2| = 2 (distância do ponto associado a 2 até a origem) CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 2

Módulo Observação Para todo x ℝ, temos: Exemplos a) = |2 – | = – (2 – ) = – 2, pois 2 – é negativo. b) = |x – 3| = c) = x ² + 1, pois x² + 1 é positivo para qualquer x ℝ. CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 3

Função modular é a função f: ℝ ℝ tal que: f(x) = | x|, ou seja, f(x) = Há algumas funções que podem ser obtidas da função modular. Exemplos a) f(x) = | x| – 3 d) j(x) = | x| + | x + 1| b) i(x) = 9| x 2 + x| e) h(x) = | – x²| + 7 c) g(x) = f) l(x) = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 4

Gráfico da função modular § Para x ≥ 0, temos: f(x) = | x| = x CONEXÕES COM A MATEMÁTICA x y = f(x) = x (x, y) 0 y = f(0) = 0 (0, 0) 1 y = f(1) = 1 (1, 1) ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 5

Gráfico da função modular § Para x < 0, temos: f(x) = | x| = – x x – 1 – 2 CONEXÕES COM A MATEMÁTICA y = f(x) = –x y = f (– 1) = –(– 1) = 1 y = f(– 2) = –(– 2) = 2 ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 5 (x, y) (– 1, 1) (– 2, 2)

Gráfico da função modular Reunindo os dois gráficos, formamos o gráfico da função modular f(x) = | x|: D( f) = ℝ e Im( f) = ℝ+ CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 5

Exercício resolvido R 1. Calcular | x + 1|para: a) x = 7 b) x = – 8 c) qualquer número real Resolução a) Para x = 7: | x + 1| = |7 + 1| = |8| = 8 b) Para x = – 8: |x + 1| = |– 8 + 1| = |– 7| = 7 c) Pela definição de módulo, temos duas possibilidades. § |x + 1| = x + 1, se x + 1 ≥ 0, ou seja, x ≥ – 1 § |x + 1| = –( x + 1), se x + 1 < 0, ou seja, x < – 1 Portanto: | x + 1| = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 6

Exercício resolvido R 2. Determinar os possíveis valores reais de a) |x| = 7 x para: c) |x| = – 3 b) |x| = 0 Resolução a) Se | x| = 7, então x = 7 ou x = – 7 Podemos verificar: |7| = 7 e |– 7| = 7 b) Se | x| = 0, então x = 0, pois zero é o único número real cujo módulo é zero. c) A sentença | x| = – 3 é falsa para qualquer número real, pois o módulo de um número real nunca é negativo. CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 7

Exercício resolvido R 3. Determine uma expressão equivalente a cada caso, sem usar módulo. a) Se | x – 5| para x > 5. b) |x – 5| – | x – 3| para x ℝ. Resolução a) Se x > 5, temos: x – 5 > 0 Portanto: | x – 5| = x – 5 para x > 5. CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 8

Exercício resolvido R 3. Resolução b) Para x ϵ ℝ, devemos analisar três casos: § Se x < 3, temos x – 5 < 0 e x – 3 < 0. Portanto: | x – 5| – | x – 3| = – x + 5 – (– x + 3) = 2 § Se 3 ≤ x ≤ 5, temos x – 5 ≤ 0 e x – 3 ≥ 0. Portanto: | x – 5| – | x – 3| = – x + 5 – ( x – 3) = – 2 x + 8 § Se x > 5, temos x – 5 > 0 e x – 3 > 0. Portanto: | x – 5| – | x – 3| = x – 5 – ( x – 3) = – 2. Logo: | x – 5| – | x – 3| = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 8

Exercício resolvido R 4. Construa o gráfico da função g(x) = | x| + 1. Resolução Para definir os pontos do gráfico, faremos duas tabelas: § para x ≥ 0, g(x) = | x| + 1 = x + 1: x y = g(x) = x + 1 (x, y) y = g(0) = 0 + (0, 1) 0 1 1 y = g(1) = 1 + 1 (1, 2) CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 9

Exercício resolvido R 4. Construa o gráfico da função g(x) = | x| + 1. Resolução Para definir os pontos do gráfico, faremos duas tabelas: § para x < 0, g(x) = | x| + 1 = – x + 1: x y = g(x) = –x + 1 (x, y) – 1 y = g(– 1) = –(– 1) + (– 1, 2) 1 – 2 y = g(– 2) = –(– 2) + 1 CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular (– 2, 3) 5. 9

Exercício resolvido R 4. Construa o gráfico da função g(x) = | x| + 1. Resolução Observe que o gráfico da função f(x) = | x| transladado 1 unidade para cima. CONEXÕES COM A MATEMÁTICA g(x) =| x| + 1 é o ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 9

Exercício resolvido R 5. Estudar o sinal da função h(x) = | x – 1| e verificar em que intervalos ela é crescente e em quais ela é decrescente. Resolução Para estudar o sinal da função, vamos construir seu gráfico. Observando que a expressão se anula para = 1, faremos §duas tabelas: Para x ≥ 1, h(x) = | x – 1| = x – 1 CONEXÕES COM A MATEMÁTICA x y = h(x) = x – 1 (x, y) 1 y = h(1) = 1 – 1 (1, 0) 2 y = h(2) = 2 – 1 (2, 1) ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 10 x

Exercício resolvido R 5. Estudar o sinal da função h(x) = | x – 1| e verificar em que intervalos ela é crescente e em quais ela é decrescente. Resolução Para estudar o sinal da função, vamos construir seu gráfico. Observando que a expressão se anula para = 1, faremos §duas tabelas: Para x < 1, h(x) = | x – 1| = – x + 1 x y = h(x) = –x + 1 (x, y) 0 y = h(0) = – 0 + 1 (0, 1) – 1 y = h(– 1) = –(– 1) + 1 CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular (– 1, 2) 5. 10 x

Exercício resolvido R 5. Estudar o sinal da função h(x) = | x – 1| e verificar em que intervalos ela é crescente e em quais ela é decrescente. Resolução Analisando o gráfico, concluímos que a função h: § é positiva para ℝ – {1}; § não tem valores negativos; § é nula para x = 1; § é decrescente em ]–∞, 1]; § é crescente em [1, +∞[. CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 10

Equações e inequações modulares Equações modulares Uma equação é chamada de equação modular quando a incógnita aparece em módulo. Exemplo Para a equação modular | x – 9| = 3 ser válida, devemos ter: x – 9 = 3 ou x – 9 = – 3 Assim: |x – 9| = 3 Logo, o conjunto solução da equação é: CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 11 S = {6, 12}

Equações e inequações modulares Inequações modulares Uma inequação é chamada de inequação modular quando a incógnita aparece em módulo. Exemplos a) |x| ≥ 28 d) 8| x 2 | > – x b) – | x| + 1 ≤ 5 e) |4 x – 3| ≥ 2 c) |x| + 1 < 25 f) |– 5 x 2 – 0, 2|< 0 CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 12

Resolução de inequações modulares Exemplos a) Vamos determinar os valores reais de x que satisfazem a inequação | x – 1|< 3. (II) |x – 1| < 3 – 3 < x – 1 < 3 (I) – 3 < x – 1 – 3 + 1 < x x > – 2 Portanto: S 1 = (II) x – 1 < 3 x < 3 + 1 x < 4 Portanto: S 2 = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 13

Resolução de inequações modulares Exemplos a) A solução final será a intersecção das soluções Logo, o conjunto solução da inequação | x – 1| < 3 é S = ou S =]– 2, 4[ CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 13 S 1 e S 2 :

Resolução de inequações modulares Exemplos a) Podemos representar geometricamente essa inequação. Considerando f(x) = | x – 1| e g(x) = 3, temos: CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 13

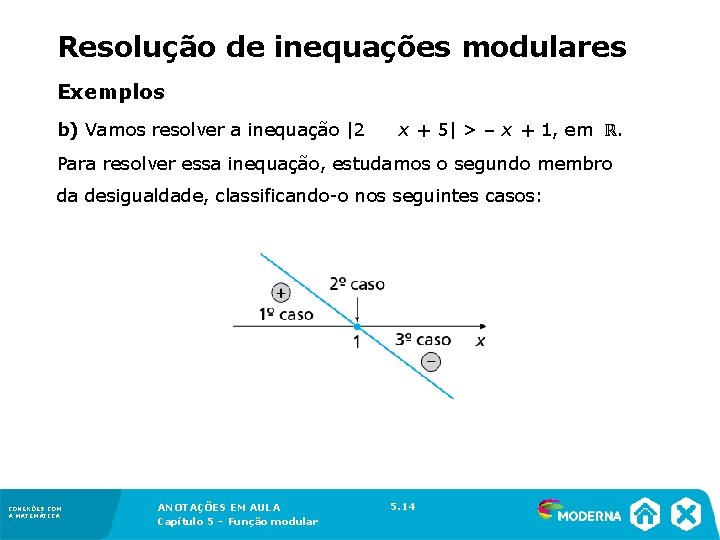
Resolução de inequações modulares Exemplos b) Vamos resolver a inequação |2 x + 5| > – x + 1, em ℝ. Para resolver essa inequação, estudamos o segundo membro da desigualdade, classificando-o nos seguintes casos: CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 14

Resolução de inequações modulares Exemplos b) A solução da inequação será a união das soluções obtidas em cada caso. 1 o caso: o segundo membro é negativo, ou seja: – x + 1 < 0 x > 1 |2 x + 5| sempre será maior que um número negativo. Assim, o conjunto solução para esse caso é: S 1 = 2 o caso: o segundo membro é nulo, ou seja: – x + 1 = 0 x = 1 Teremos uma desigualdade verdadeira, pois: |2 x + 5| > – 1 + 1 |7| > 0 7 > 0 (verdadeiro) Assim, o conjunto solução para esse caso é: S 2 = {1} CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 14

Resolução de inequações modulares Exemplos b) 3 o caso: o segundo membro é positivo, ou seja: –x + 1 > 0 x < 1. Teremos: |2 x + 5| > – x + 1 2 x + 5 < –(– x + 1) ou 2 x + 5 > – x + 1 Resolvendo as duas inequações: (I) 2 x + 5 < –(– x + 1) 2 x + 5 < x – 1 2 x – x < – 1 – 5 x < – 6 (II) 2 x + 5 > – x + 1 2 x + x > 1 – 5 3 x > – 4 x > CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 14

Resolução de inequações modulares Exemplos b) Como a inequação modular gerou duas possibilidades, a inequação (I) ou a inequação (II), a solução para esse caso é a união das soluções parciais: CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 14

Resolução de inequações modulares Exemplos b) Lembrando que essa solução é válida apenas para temos: x < 1, S 3 = Para finalizar, vamos unir as soluções encontradas em cada caso: Logo, o conjunto solução da inequação |2 S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 14 x + 5| > – x + 1 é:

Resolução de inequações modulares Exemplos c) Agora vamos determinar os valores reais de satisfazem a inequação | x que x 2 | < 1. (II) |x 2 | < 1 – 1 < x 2 < 1 (I) x 2 > – 1 Esta inequação é válida para todo x real. Portanto: S 1 = ℝ (II) x 2 < 1 x 2 – 1 < 0 Portanto: S 2 = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 15

Resolução de inequações Exemplos c) A solução final será a intersecção das soluções Logo: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 15 S 1 e S 2 :

Identificação do domínio de uma função por meio de inequações Exemplos a) Vamos identificar o domínio da função dada pela lei . (I) (II) Para , temos: ≠ 0 e > 0. (I) 0 (II) x – 1 > 0 x > 1 x e x CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 16

Identificação do domínio de uma função por meio de inequações Exemplos a) Como as condições (I) e (II) devem ocorrer juntas, fazemos a intersecção das soluções parciais para obter o domínio, ou seja, D = (I) ⋂ (II). Logo: D = { x ϵ ℝ�� x > 1 e x } CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 16

Identificação do domínio de uma função por meio de inequações Exemplos b) Agora vamos identificar o domínio da função . Para , temos: (II) ≥ 0 – 3 (I) – 3 ≤ x + 2 x ≥ – 5 CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular (II) x + 2 ≤ 3 x ≤ 1 5. 17

Identificação do domínio de uma função por meio de inequações Exemplos b) Para obter o domínio da função, devemos intersecção das soluções parciais, ou seja, D = (I) Logo: D = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 17 fazer a ⋂ (II):

Exercício resolvido R 6. Resolver a equação modular |3 Resolução |3 x – 9| = | x + 5| Resolvendo as equações, temos: 3 x – 9 = x + 5 3 x – 9 = – x – 5 3 x – x = 5 + 9 3 x + x = – 5 + 9 2 x = 14 4 x = 4 x = 7 x = 1 Portanto: S = {1, 7} CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 18 x – 9| = | x + 5|.

Exercício resolvido R 7. Determinar o conjunto solução da equação modular |4 x – 1| = x + 4. Resolução A condição inicial para encontrar a solução dessa equação é admitir: x + 4 ≥ 0 ⇒ x ≥ – 4 Em seguida, procedemos como nos exercícios anteriores. |4 x – 1| = x + 4 CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 19

Exercício resolvido R 7. Determinar o conjunto solução da equação modular |4 x – 1| = x + 4. Resolução 4 x – 1 = x + 4 4 x – 1 = – x – 4 4 x – x = 4 + 1 4 x + x = – 4 + 1 3 x = 5 5 x = – 3 x = Como e satisfazem a condição inicial e (x ≥ – 4), concluímos que: CONEXÕES COM A MATEMÁTICA S = 5. 19 ANOTAÇÕES EM AULA Capítulo 5 – Função modular

Exercício resolvido R 8. Determinar a solução da equação modular |2 x 2 – 7 x + 3| = 0. Resolução |2 x 2 – 7 x + 3| = 0 2 x 2 – 7 x + 3 = 0 = (– 7) 2 – 4 ∙ 2 ∙ 3 = 49 – 24 = 25 Portanto: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 20

Exercício resolvido R 9. Determinar a solução da equação modular 4| x| 2 + 11| x| – 3 = 0. Resolução Fazendo | x| = y, obtemos: 4 y 2 + 11 y – 3 = 0 = (11) 2 – 4 ∙ (– 3) = 121 + 48 = 169 CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 21

Exercício resolvido R 9. Determinar a solução da equação modular 4| x| 2 + 11| x| – 3 = 0. Resolução Como | x| = y, então y = – 3 não será possível. Logo: | x| = x = ou x = Portanto: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 21

Exercício resolvido R 10. Obter, em ℝ, o conjunto solução das inequações modulares. a) |2 x + 1| > 5 c) |5 x + 1| ≤ 3 b) |3 x + 1| < – 4 d) |7 x + 1| > – 9 Resolução a) |2 x + 1| > 5 2 x + 1 < – 5 ou 2 x + 1 > 5 2 x < – 6 ou 2 x > 4 x < – 3 ou x > 2 Portanto: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 22

Exercício resolvido R 10. Obter, em ℝ, o conjunto solução das inequações modulares. a) |2 x + 1| > 5 c) |5 x + 1| ≤ 3 b) |3 x + 1| < – 4 d) |7 x + 1| > – 9 Resolução b) Como |3 x + 1| é positivo ou nulo para todo sentença |3 x + 1| < – 4 é falsa. Portanto: S = ∅ CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 22 x real, a

Exercício resolvido R 10. Obter, em ℝ, o conjunto solução das inequações modulares. a) |2 x + 1| > 5 c) |5 x + 1| ≤ 3 b) |3 x + 1| < – 4 d) |7 x + 1| > – 9 Resolução c) |5 x + 1| ≤ 3 – 3 ≤ 5 x + 1 ≤ 3 – 4 ≤ 5 x ≤ 2 Portanto: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 22

Exercício resolvido R 10. Obter, em ℝ, o conjunto solução das inequações modulares. a) |2 x + 1| > 5 c) |5 x + 1| ≤ 3 b) |3 x + 1| < – 4 d) |7 x + 1| > – 9 Resolução d) Como |7 x + 1| é positivo ou nulo para todo x real, a sentença |7 x + 1| > – 9 é verdadeira, qualquer que seja x real. Portanto: S = ℝ CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 22

Exercício resolvido R 11. Determine, em ℝ, o conjunto solução das inequações modulares. a) |x 2 – 5 x| > 6 b) |x 2 – x – 4| < 2 Resolução a) |x 2 – 5 x| > 6 x 2 – 5 x < – 6 ou x 2 – 5 x > 6 (I) CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular (II) 5. 23

Exercício resolvido R 11. Determine, em ℝ, o conjunto solução das inequações modulares. a) |x 2 – 5 x| > 6 b) |x 2 – x – 4| < 2 Resolução a) (I) x 2 – 5 x < – 6 (II) x 2 – 5 x > 6 x 2 – 5 x + 6 < x 2 – 5 x – 6 > 0 0 S 2 = S 1 = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 23

Exercício resolvido R 11. Determine, em ℝ, o conjunto solução das inequações modulares. a) |x 2 – 5 x| > 6 b) |x 2 – x – 4| < 2 Resolução a) A solução final será a união das soluções Portanto: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 23 S 1 e S 2.

Exercício resolvido R 11. Determine, em ℝ, o conjunto solução das inequações modulares. a) |x 2 – 5 x| > 6 b) |x 2 – x – 4| < 2 Resolução b) |x 2 – x – 4| < 2 ⇔ – 2 < x 2 – x – 4 < 2 x 2 – x – 4 > – 2 e x 2 – x – 4 < 2 (I) CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular (II) 5. 23

Exercício resolvido R 11. Determine, em ℝ, o conjunto solução das inequações modulares. a) |x 2 – 5 x| > 6 b) |x 2 – x – 4| < 2 Resolução (I) x 2 – x – 4 > – (II) x 2 – x – 4 < 2 2 x 2 – x – 6 > 0 x 2 – x – 2 > 0 S 1 = CONEXÕES COM A MATEMÁTICA S 2 = ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 23

Exercício resolvido R 11. Determine, em ℝ, o conjunto solução das inequações modulares. a) |x 2 – 5 x| > 6 b) |x 2 – x – 4| < 2 Resolução b) Nesse caso, a solução final será a intersecção das soluções S 1 e S 2. Portanto: S = CONEXÕES COM A MATEMÁTICA ANOTAÇÕES EM AULA Capítulo 5 – Função modular 5. 23

ANOTAÇÕES EM AULA Coordenação editorial: Juliane Matsubara Barroso Edição de texto: Ana Paula Souza Nani, Adriano Rosa Lopes, Enrico Briese Casentini, Everton José Luciano, Juliana Ikeda, Marilu Maranho Tassetto, Willian Raphael Silva Assistência editorial: Pedro Almeida do Amaral Cortez Preparação de texto: Renato da Rocha Carlos Coordenação de produção: Maria José Tanbellini Iconografia: Daniela Chahin Barauna, Erika Freitas, Fernanda Siwiec, Monica de Souza e Yan Comunicação Ilustração dos gráficos: Adilson Secco EDITORA MODERNA Diretoria de Tecnologia Educacional Editora executiva: Kelly Mayumi Ishida Coordenadora editorial: Ivonete Lucirio Editores: Andre Jun, Felipe Jordani e Natália Coltri Fernandes Assistentes editoriais: Ciça Japiassu Reis e Renata Michelin Editor de arte: Fabio Ventura Editor assistente de arte: Eduardo Bertolini Assistentes de arte: Ana Maria Totaro, Camila Castro e Valdeí Prazeres Revisores: Antonio Carlos Marques, Diego Rezende e Ramiro Morais Torres © Reprodução proibida. Art. 184 do Código Penal e Lei 9. 610 de 19 de fevereiro de 1998. Todos os direitos reservados. EDITORA MODERNA Rua Padre Adelino, 758 – Belenzinho São Paulo – SP – Brasil – CEP: 03303 -904 Vendas e atendimento: Tel. (0__11) 2602 -5510 Fax (0__11) 2790 -1501 www. moderna. com. br 2012 CONEXÕES COM A MATEMÁTICA