Funciones o Seales Singulares Las secuencias discretas impulso












- Slides: 19

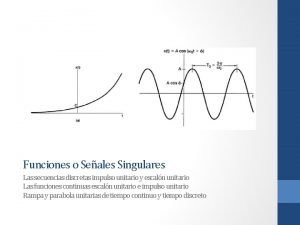
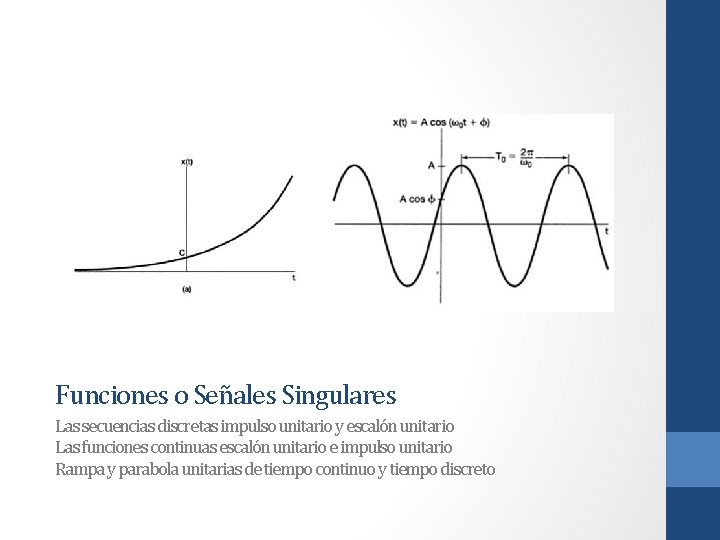
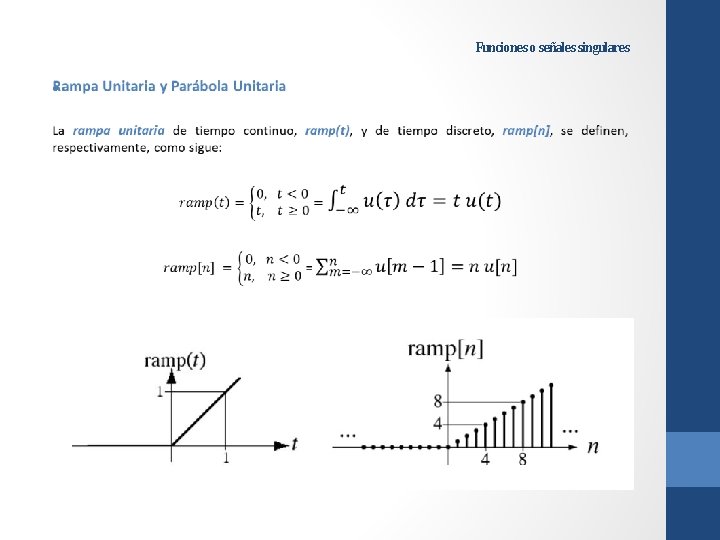
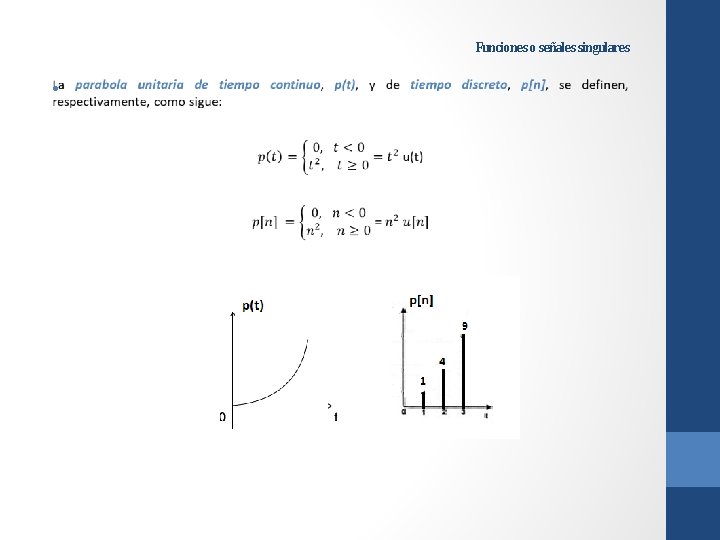
Funciones o Señales Singulares Las secuencias discretas impulso unitario y escalón unitario Las funciones continuas escalón unitario e impulso unitario Rampa y parabola unitarias de tiempo continuo y tiempo discreto

Funciones o señales singulares Las Funciones Impulso Unitario y Escalón Unitario En esta clase se presentan otras señales básicas, conocidas también como funciones singulares – específicamente, las funciones impulso unitario, escalón unitario, rampa unitaria y parábola unitaria, tanto continuas como discretas- que son de importancia considerable en el análisis de señales y sistemas. En clases posteriores, se verá cómo se pueden usar las señales impulso unitario como bloques fundamentales básicos para Ia construcción y representación de otras señales. Las secuencias discretas impulso unitario y escalón unitario Una de las señales discretas más simples es el impulso unitario (o muestra unitaria), la cual se define como y está representada en la figura 1. 28. En adelante, se referirá a δ[n] indistintamenle como impulso unitario o muestra unitaria.

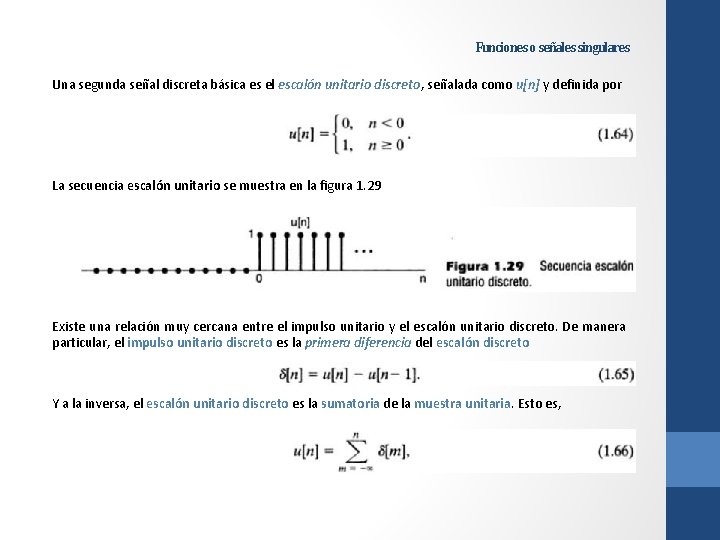
Funciones o señales singulares Una segunda señal discreta básica es el escalón unitario discreto, señalada como u[n] y definida por La secuencia escalón unitario se muestra en la figura 1. 29 Existe una relación muy cercana entre el impulso unitario y el escalón unitario discreto. De manera particular, el impulso unitario discreto es la primera diferencia del escalón discreto Y a la inversa, el escalón unitario discreto es la sumatoria de la muestra unitaria. Esto es,

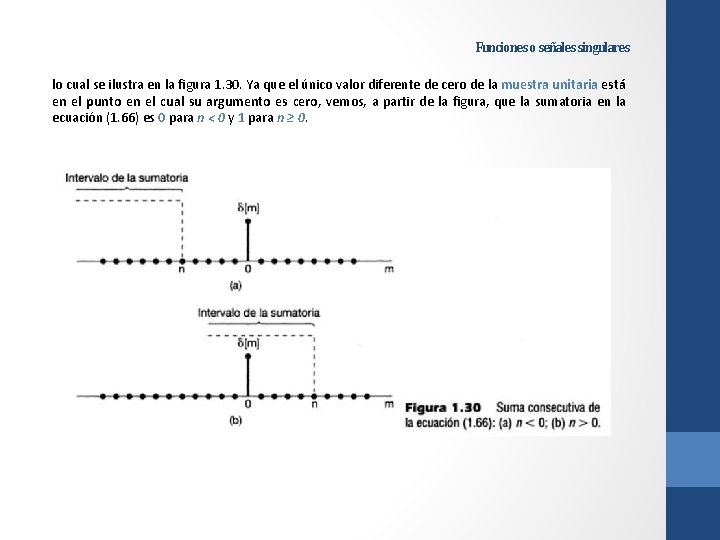
Funciones o señales singulares lo cual se ilustra en la figura 1. 30. Ya que el único valor diferente de cero de la muestra unitaria está en el punto en el cual su argumento es cero, vemos, a partir de la figura, que la sumatoria en la ecuación (1. 66) es 0 para n < 0 y 1 para n ≥ 0.

Funciones o señales singulares Además, cambiando la variable de Ia sumatoria de m a k = n - m en In ecuación (1. 66), encontramos que el escalón unitario discreto también se puede escribir en términos de la muestra unitaria como o de manera equivalente, La ecuación (1. 67) se ilustra en la figura 1. 31. En este caso el valor diferente de cero de δ[n - k] se encuentra en el valor de k igual a n, por lo cual nuevamente vemos que la sumatoria en la ecuación (1. 67) es 0 para n < 0 y 1 para n ≥ 0.

Funciones o señales singulares •

Funciones o señales singulares Las señales continuas impulso unitario y escalón unitario La función escalón unitario u(t) continua se define de manera similar a su contraparte discreta. Específicamente como se muestra en la figura 1. 32. Obsérvese que el escalón unitario es discontinuo en t = 0. La función impulso unitario δ(t) continua está relacionada con el escalón unitario de manera análoga a la relación que existe entre las funciones discretas impulso unitario y escalón unitario.

Funciones o señales singulares •

Funciones o señales singulares •

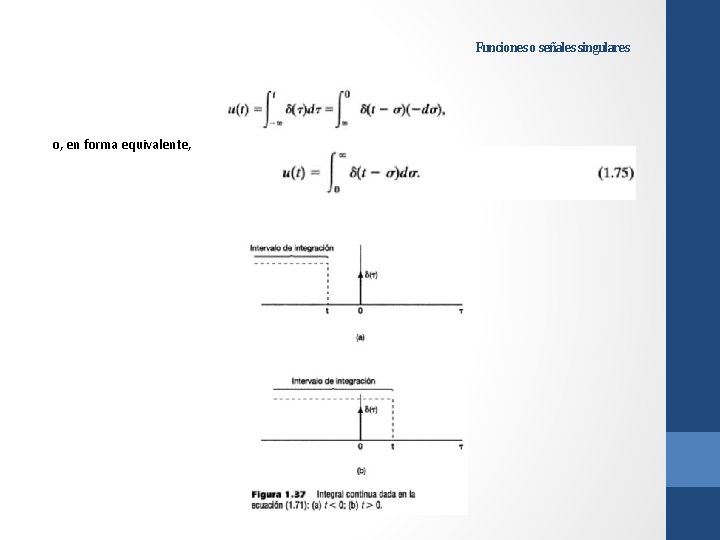
Funciones o señales singulares La figura 1. 36 muestra un impulso escalado con área k, donde se buscó que la altura de la flecha utilizada para representar el impulso escalado fuera proporcional al área del impulso. Al igual que en tiempo discreto, podemos proporcionar una interpretación gráfica sencilla de la integral continua de la ecuación (1. 71); esto se muestra en la figura 1. 37. Ya que el área del impulso unitario continuo δ(t) está concentrada en t = 0, vemos que la integral continua es 0 para t < 0 y 1 para t > 0. También observamos que la relación en la ecuación (1. 71) entre el escalón y el impulso unitario continuos puede rescribirse en forma diferente, análoga a la forma discreta de la ecuación (1. 67), cambiando la variable de integración de τ a σ = t - τ.

Funciones o señales singulares o, en forma equivalente,

Funciones o señales singulares La interpretación gráfica de esta forma de relación entre u(t) y δ(t) se muestra en la figura 1. 38. Puesto que en este caso el área de δ(t - σ) está concentrada en el punto σ = t, de nuevo vemos que la integral en la ecuación (1. 75) es 0 para t < 0 y 1 para t > 0.

Funciones o señales singulares •

Funciones o señales singulares •

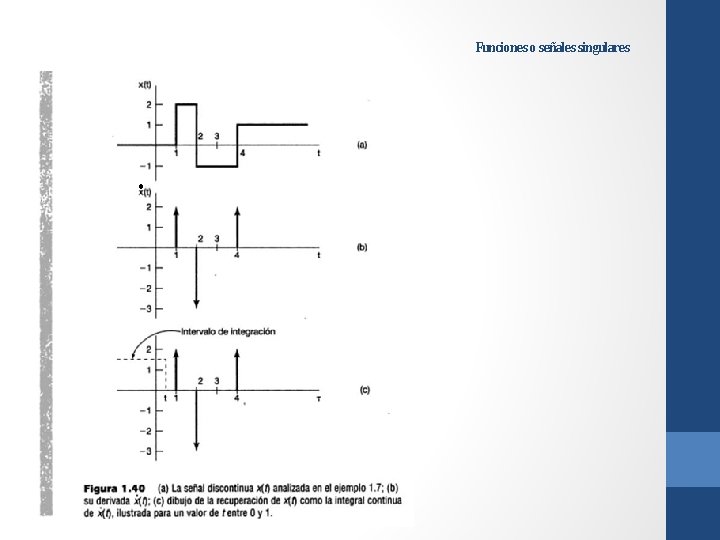
Funciones o señales singulares Cualquier sistema físico real tiene algo de inercia asociada con él y entonces no responde instantáneamente a las entradas. En consecuencia, si un pulso de duración lo suficientemente corta se aplica a esos sistemas, la respuesta del sistema no será influenciada de forma perceptible por la duración del pulso o por los detalles de la forma del pulso. En cambio, la principal característica del pulso que realmente importará es el efecto neto integrado del pulso, es decir, su área. Para sistemas que responden mucho más rápido que otros, el pulso tendrá que ser de duración mucho más corta antes de que los detalles de la forma del pulso o su duración pierdan importancia. No obstante, para cualquier sistema físico, siempre se puede encontrar un pulso que sea "suficientemente corto". Por tanto, el impulso unitario es una idealización de este concepto --el pulso que es bastante corto para cualquier sistema--. Como se verá próximamente, la respuesta de un sistema a este pulso idealizado juega un papel crucial en el análisis de sistemas y señales, y en el proceso de desarrollo y comprensión de este papel, se ofrecerá un conocimiento adicional sobre la señal idealizada.

Funciones o señales singulares

Funciones o señales singulares

Funciones o señales singulares •

Funciones o señales singulares •
 Señal rampa
Señal rampa Variable ordinal
Variable ordinal Variable aleatoria continua normal
Variable aleatoria continua normal Estadstica
Estadstica Características de la destreza motora
Características de la destreza motora Señales discretas y continuas
Señales discretas y continuas Recorrido posorden
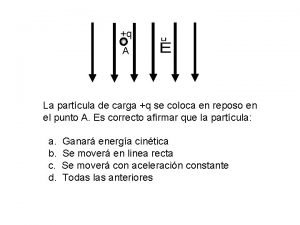
Recorrido posorden Carga puntual
Carga puntual Discretizar
Discretizar Formula de poisson
Formula de poisson Estructuras discretas pucp
Estructuras discretas pucp Textos con secuencias textuales ejemplos
Textos con secuencias textuales ejemplos Funciones de palabras
Funciones de palabras Todos somos singulares
Todos somos singulares Punto ordinario
Punto ordinario Puntos singulares ecuaciones diferenciales
Puntos singulares ecuaciones diferenciales El primer impulso de un corazon regenerado
El primer impulso de un corazon regenerado Partcula
Partcula Nervinio impulso sklidimo kelias
Nervinio impulso sklidimo kelias Momento lineal e impulso
Momento lineal e impulso