CONTENIDOS TASA DE VARIACIN MEDIA TASA DE VARIACIN

CONTENIDOS ØTASA DE VARIACIÓN MEDIA. TASA DE VARIACIÓN INSTANTÁNEA O DERIVADA. ØINTERPRETACIÓN GEOMÉTRICA: RECTA TANGENTE A UNA CURVA EN UN PUNTO. ØFUNCIÓN DERIVADAS SUCESIVAS. ØCONTINUIDAD Y DERIVABILIDAD. ØDERIVACIÓN LOGARÍTMICA. ØDERIVACIÓN IMPLÍCITA. ØDIFERENCIAL DE UNA FUNCIÓN. ØTEOREMA DE ROLLE. ØTEOREMA DEL VALOR MEDIO. ØREGLA DE L’HÔPITAL. ØAPLICACIONES DE LA DERIVADA: MONOTONÍA Y CURVATURA. ØAPLICACIONES DE LA DERIVADA: EXTREMOS RELATIVOS.

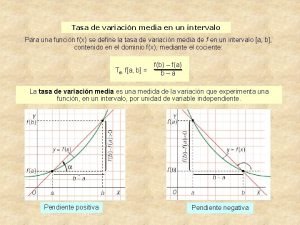
TASA DE VARIACIÓN Dada una función f: A , se llama TASA DE VARIACIÓN de f para el intervalo (a, b) a f(b) – f(a) Ejemplos f(x) = 5 x – 1 en el intervalo (-2, 3) f(3) = 5· 3 – 1 = 14 f(-2) = 5·(-2) – 1 = -11 T. V. = 14 – (-11) = 25 g(x) = tgx en el intervalo (- /4, /4) g( /4) = tg( /4) = 1 g(- /4) = tg(- /4) = -1 T. V. = 1 – (-1) = 2 MÁS EJEMPLOS

TASA DE VARIACIÓN MEDIA Dada una función f: A , se llama TASA DE VARIACIÓN MEDIA de f para el intervalo (a, b) al cociente f(b) – f(a) b–a Ejemplos f(x) = 5 x – 1 en el intervalo (-2, 3) T. V. = 14 – (-11) = 25 T. V. M. = 25/[3 – (-2)] = 25/5 = 5 g(x) = tgx en el intervalo (- /4, /4) T. V. = 1 – (-1) = 2 T. V. M. = 2/[ /4 – (- /4)] = 4/ MÁS EJEMPLOS

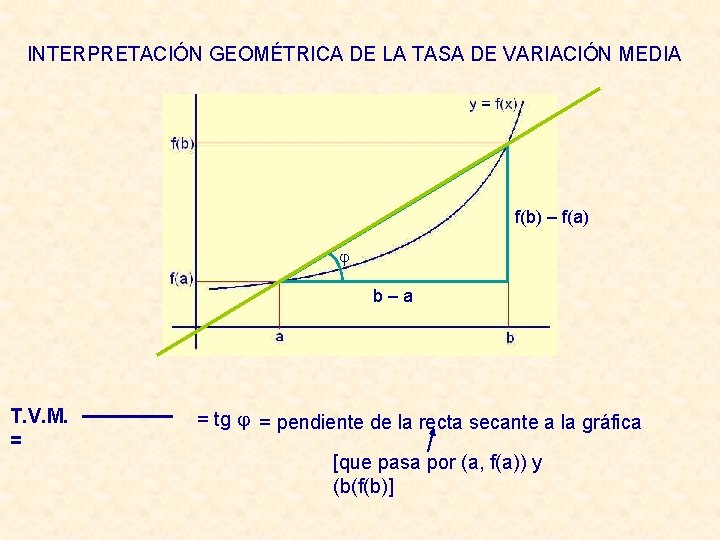
INTERPRETACIÓN GEOMÉTRICA DE LA TASA DE VARIACIÓN MEDIA f(b) – f(a) b–a T. V. M. = = tg = pendiente de la recta secante a la gráfica [que pasa por (a, f(a)) y (b(f(b)]

TASA DE VARIACIÓN INSTANTÁNEA DERIVADA Dada una función f: A , se llama TASA DE VARIACIÓN INSTANTÁNEA de f para x = a, al límite: = lim h 0 f(a + h) – f(a) h La tasa de variación instantánea en x = a, también se llama DERIVADA de la función f en x = a, y se denota f ’(a) Ejemplos Tasa de variación instantánea de f(x) = 5 x – 1 en x = 2 f(2) = 5· 2 – 1 = 9 f(2 + h) – f(2) = 9 + 5 h -9 5 h = =5 h h h f(2 + h) = 5·(2+ h) – 1 = 9 + 5 h Por tanto: f ‘(2) = MÁS EJEMPLOS lim h 0 f(2 + h) – f(2) = h lim 5=5 h 0

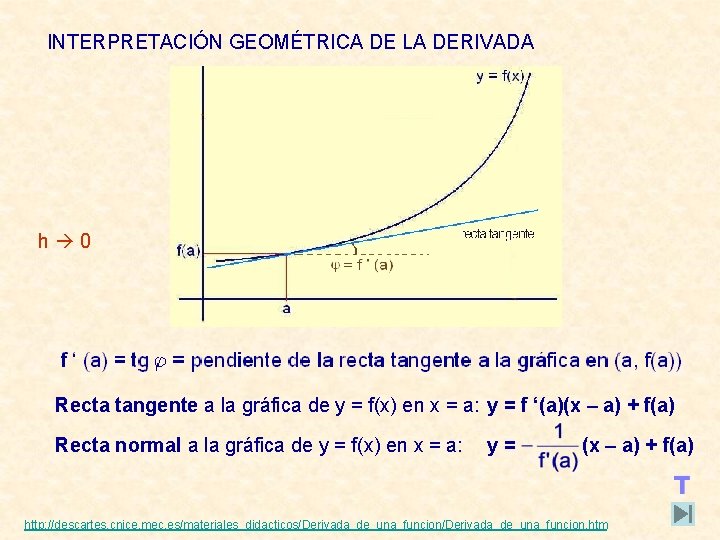
INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA h 0 f(a+h) – f(a) T. V. M. = tg = pendiente de la recta secante a la gráfica h = Recta tangente a la gráfica de y = f(x) en x = a: y = f ‘(a)(x – a) + f(a) Recta normal a la gráfica de y = f(x) en x = a: y= (x – a) + f(a) http: //descartes. cnice. mec. es/materiales_didacticos/Derivada_de_una_funcion. htm

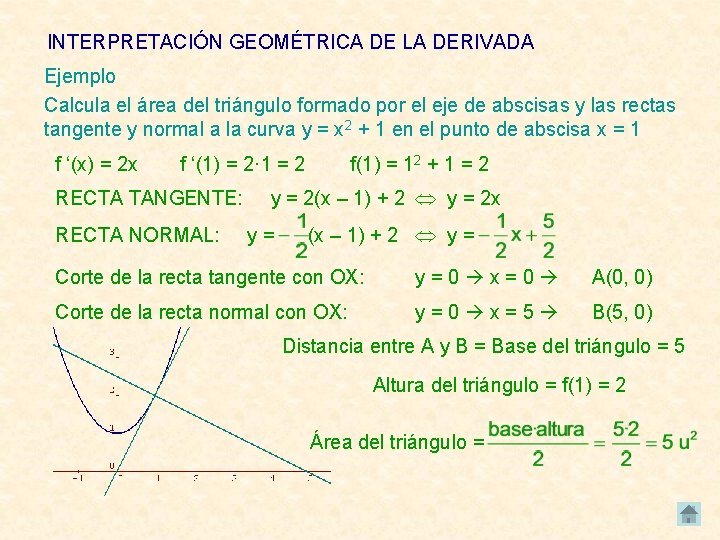
INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA Ejemplo Calcula el área del triángulo formado por el eje de abscisas y las rectas tangente y normal a la curva y = x 2 + 1 en el punto de abscisa x = 1 f ‘(x) = 2 x f ‘(1) = 2· 1 = 2 RECTA TANGENTE: RECTA NORMAL: f(1) = 12 + 1 = 2 y = 2(x – 1) + 2 y = 2 x y= (x – 1) + 2 y = Corte de la recta tangente con OX: y=0 x=0 A(0, 0) Corte de la recta normal con OX: y=0 x=5 B(5, 0) Distancia entre A y B = Base del triángulo = 5 Altura del triángulo = f(1) = 2 Área del triángulo =

FUNCIÓN DERIVADAS SUCESIVAS. La función que a cada x Domf le hace corresponder f ‘(x), si existe, se llama función derivada de f, o simplemente, derivada de f, y se escribe f ‘ Del mismo modo, podemos hablar de la derivada de f ‘, que representamos por f ”(x) y que se llama derivada segunda de f Análogamente podemos hablar de derivada tercera, cuarta, etc. En general nos referiremos a la derivada de orden n o derivada n-sima de f; f(n)(x) DERIVADAS LATERALES Derivada lateral de f(x) en x = a por la izquierda: Derivada lateral de f(x) en x = a por la derecha: Una función f es derivable en x = a si y sólo si existen y son iguales f ‘(a –) y f ‘(a+)

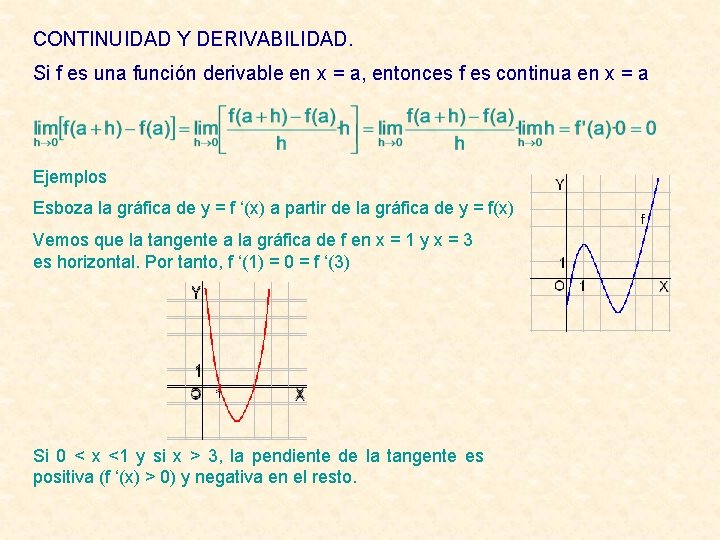
CONTINUIDAD Y DERIVABILIDAD. Si f es una función derivable en x = a, entonces f es continua en x = a Ejemplos Esboza la gráfica de y = f ‘(x) a partir de la gráfica de y = f(x) Vemos que la tangente a la gráfica de f en x = 1 y x = 3 es horizontal. Por tanto, f ‘(1) = 0 = f ‘(3) Si 0 < x <1 y si x > 3, la pendiente de la tangente es positiva (f ‘(x) > 0) y negativa en el resto.

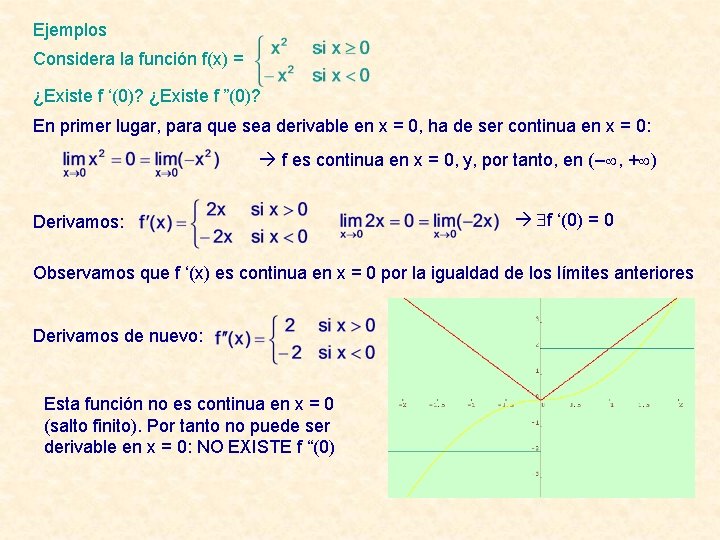
Ejemplos Considera la función f(x) = ¿Existe f ‘(0)? ¿Existe f ”(0)? En primer lugar, para que sea derivable en x = 0, ha de ser continua en x = 0: f es continua en x = 0, y, por tanto, en (– , + ) Derivamos: f ‘(0) = 0 Observamos que f ‘(x) es continua en x = 0 por la igualdad de los límites anteriores Derivamos de nuevo: Esta función no es continua en x = 0 (salto finito). Por tanto no puede ser derivable en x = 0: NO EXISTE f “(0)

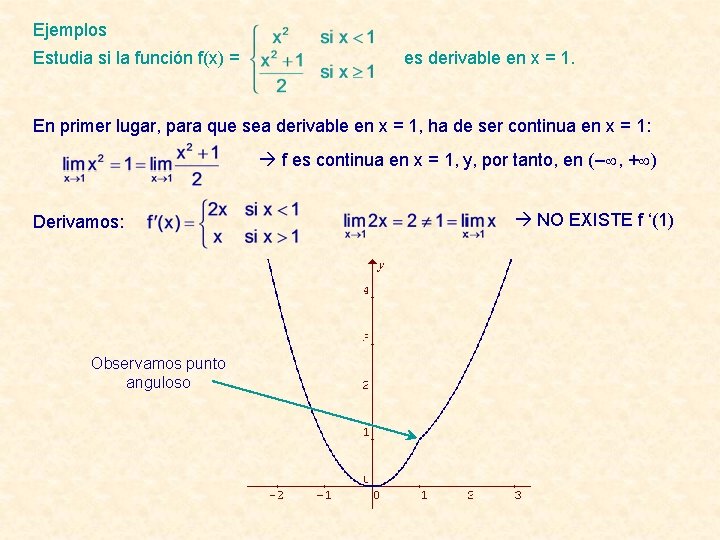
Ejemplos Estudia si la función f(x) = es derivable en x = 1. En primer lugar, para que sea derivable en x = 1, ha de ser continua en x = 1: f es continua en x = 1, y, por tanto, en (– , + ) Derivamos: Observamos punto anguloso NO EXISTE f ‘(1)

Ejemplos Considera la función f: [0, 4] R definida por f(x) = Sabiendo que f es derivable en todo el dominio y que verifica f(0) = f(4), determina los valores de a, b y c. Por ser derivable, ha de ser continua: f es derivable: f ‘(x) = Y de la condición de ser f(0) = f(4): 2 c = 4 + 2 a + b [1] c=4+a [2] 4 c = b [3] Resolviendo el sistema de ecuaciones formado por [1], [2] y [3]: a = – 3, b = 4, c = 1

DERIVACIÓN LOGARÍTMICA Se llama así a la técnica empleada para derivar funciones con cierto grado de complejidad que se simplifica al tomar logaritmos previamente. Ejemplo 1: Se toman logaritmos: Ly = Lxx = x. Lx Se deriva: Despejamos y’: y’ = y(Lx + 1) Sustituimos y: y’ = xx(Lx + 1) Ejemplo 2: Se toman logaritmos: Se deriva: Despejamos y’: Sustituimos y: Ly = L(x 2 + 1)senx = senx·L(x 2+1)

DERIVACIÓN IMPLÍCITA A veces, o bien no se puede, o es complicado despejar en una igualdad la variable dependiente para poder derivar después. En estos casos es útil el método de derivación implícita. Ejemplo 1: Obtén la ecuación de la tangente a la curva xy 5 – y 2 + x 3 = 9 en el punto P(2, 1) Derivamos directamente ambos miembros de la igualdad: 1·y 5 + x· 5 y 4·y’ – 2 y·y’ + 3 x 2 = 0 y 5 + 3 x 2 = (2 y – 5 xy 4)·y’ Calculamos la derivada en el punto P sustituyendo x por 2 e y por 1: La recta tangente es:

DIFERENCIAL DE UNA FUNCIÓN QR = f(x + h) – f(x) = y f(x + h) = f(x) + y ≈ f(x) + dy = f(x) + f ‘(x)dx Por tanto, tenemos una aproximación lineal: f(x + h) ≈ f(x) + f ‘(x)·dx Ejemplo 1: Obtén una aproximación de Tomamos f(x) = Consideramos dx = 32, 3 – 32 = 0, 3 Entonces: Usando la calculadora, obtenemos:

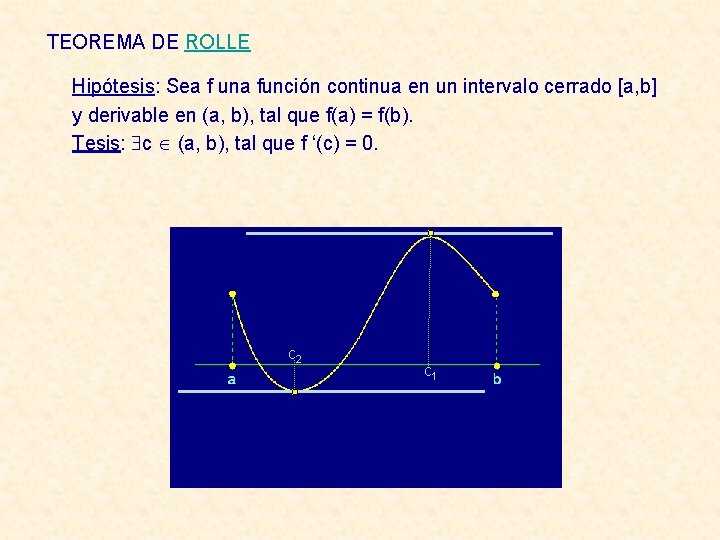
TEOREMA DE ROLLE Hipótesis: Sea f una función continua en un intervalo cerrado [a, b] y derivable en (a, b), tal que f(a) = f(b). Tesis: c (a, b), tal que f ‘(c) = 0. c 2 c c 1

TEOREMA DE ROLLE. Ejemplo Demuestra que la función f(x) = x 2 – xsenx – cosx sólo corta dos veces al eje OX. En primer lugar, utilizaremos el teorema de Bolzano para probar que corta dos veces, al menos, el eje horizontal. f es una función continua en cualquier intervalo cerrado, puesto que resulta de componer polinomios con funciones seno y coseno. Por otra parte: f(– ) = 2 + 1 > 0 f(0) = – 1 f( ) = 2 + 1 > 0 Es posible, entonces, aplicar el teorema de Bolzano en los intervalos [– , 0] y [0, ] y afirmar que la gráfica de f(x) corta al eje de abscisas al menos una vez en (– , 0) y, al menos una vez, en (0, ). Si cortara más de dos veces el eje OX, aplicando el teorema de Rolle, la derivada se anularía en más de un punto. f ‘(x) = 2 x – senx – xcosx + senx = x(2 – cosx) Observamos que f ‘(x) = 0 x = 0. Es decir, la solución es única. Así pues, sólo puede cortar el eje de abscisas dos veces.

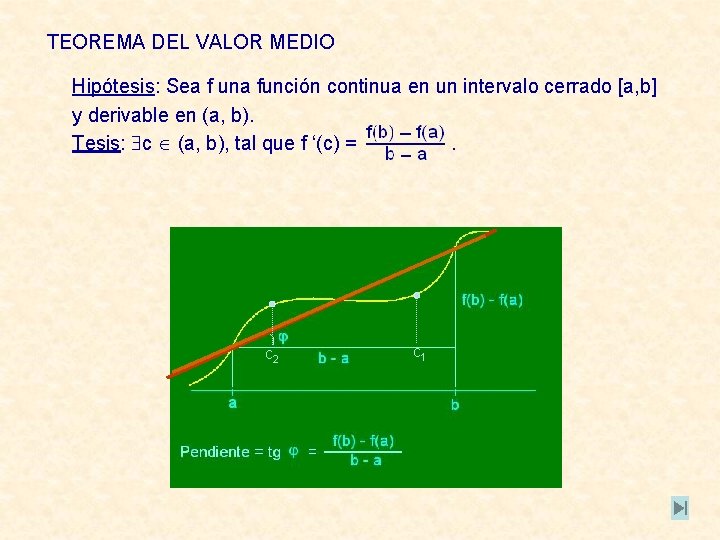
TEOREMA DEL VALOR MEDIO Hipótesis: Sea f una función continua en un intervalo cerrado [a, b] y derivable en (a, b). Tesis: c (a, b), tal que f ‘(c) =. c 2 c c 1

TEOREMA DEL VALOR MEDIO. Ejemplo Sea la función f(x) = Comprueba que f verifica las hipótesis del teorema del valor medio en el intervalo [0, 4] y halla el número c cuya existencia asegura dicho teorema. Primero comprobamos si f(x) es continua en x = 1 y en x = 2 (en el resto lo es por ser polinómica). continua en x = 1 continua en x = 2 Estudiamos la derivabilidad: derivable en x = 1; f ‘(1) = 12 derivable en x = 2; f ‘(2) = 0

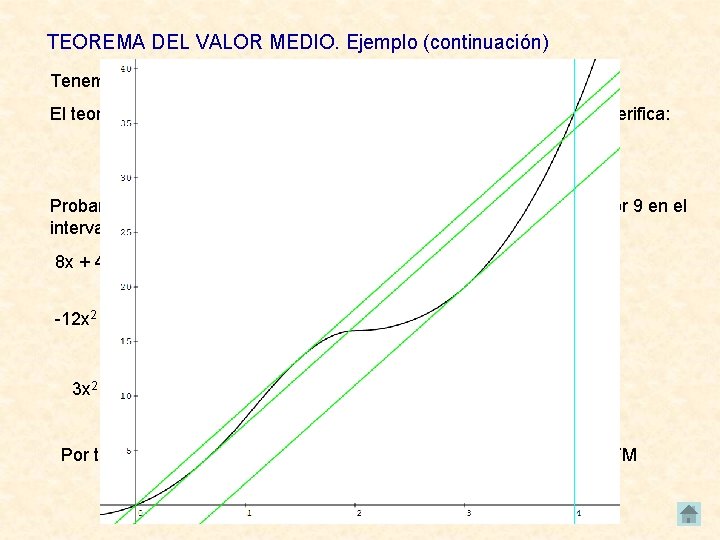
TEOREMA DEL VALOR MEDIO. Ejemplo (continuación) Tenemos, pues, que f(x) es continua en [0, 4], y derivable en (0, 4) El teorema del valor medio afirma que existe un c (0, 4) en el que se verifica: Probaremos cuál de las expresiones de la derivada puede tomar el valor 9 en el intervalo indicado (0, 4) 8 x + 4 = 9 x = 5/8 (0, 4) ( , 1] -12 x 2 3 x 2 + 24 x = 9 – 6 x = 9 12 x 2 3 x 2 – 24 x + 9 = 0 – 6 x – 9 = 0 x 1 = 1/2 ∉ (0, 4) (1, 2) x 2 = 3/2 (0, 4) (1, 2) x 1 = – 1 ∉ (0, 4) (2, + ) x 2 = 3 (0, 4) (2, + ) Por tanto, hay 3 valores del intervalo (0, 4) en los que se cumple el TVM

REGLA DE L’HÔPITAL Sean dos funciones f y g tales que Si existe , entonces existe y Ejemplo 1: Calcula Aplicamos L’Hôpital derivando numerador y denominador: La regla también es aplicable en el caso de las indeterminaciones del tipo Ejemplo 2: Calcula Aplicamos L’Hôpital derivando numerador y denominador: (De nuevo L’Hôpital)

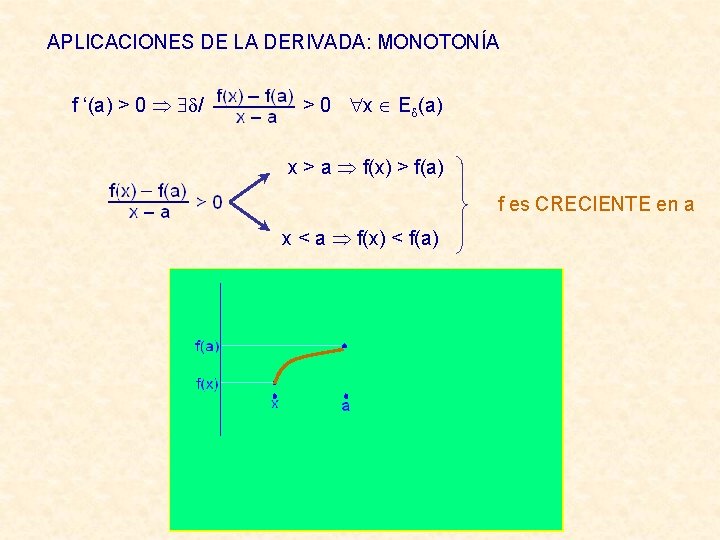
APLICACIONES DE LA DERIVADA: MONOTONÍA f ‘(a) > 0 / > 0 x E (a) x > a f(x) > f(a) f es CRECIENTE en a x < a f(x) < f(a)

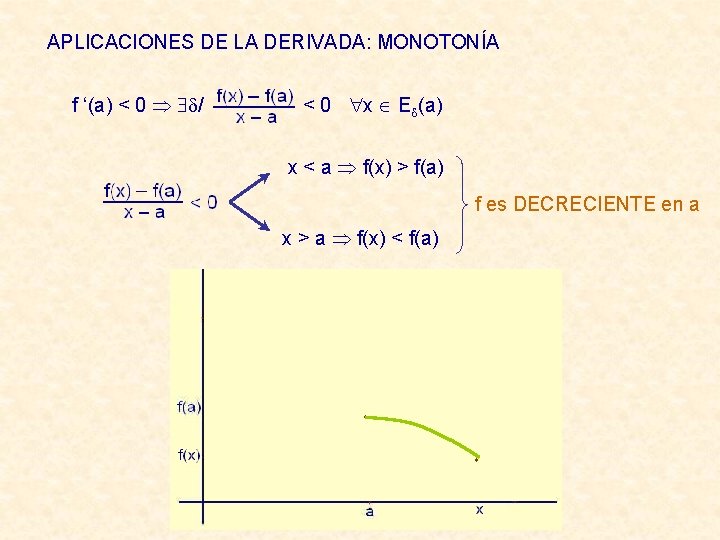
APLICACIONES DE LA DERIVADA: MONOTONÍA f ‘(a) < 0 / < 0 x E (a) x < a f(x) > f(a) f es DECRECIENTE en a x > a f(x) < f(a)

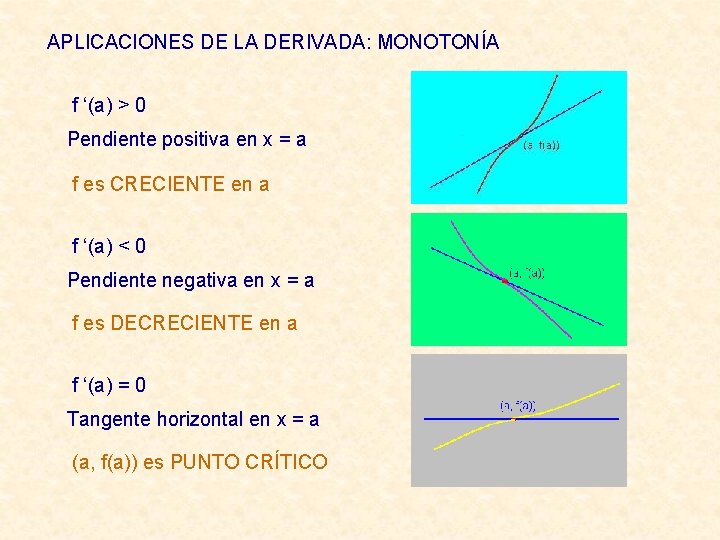
APLICACIONES DE LA DERIVADA: MONOTONÍA f ‘(a) > 0 Pendiente positiva en x = a f es CRECIENTE en a f ‘(a) < 0 Pendiente negativa en x = a f es DECRECIENTE en a f ‘(a) = 0 Tangente horizontal en x = a (a, f(a)) es PUNTO CRÍTICO

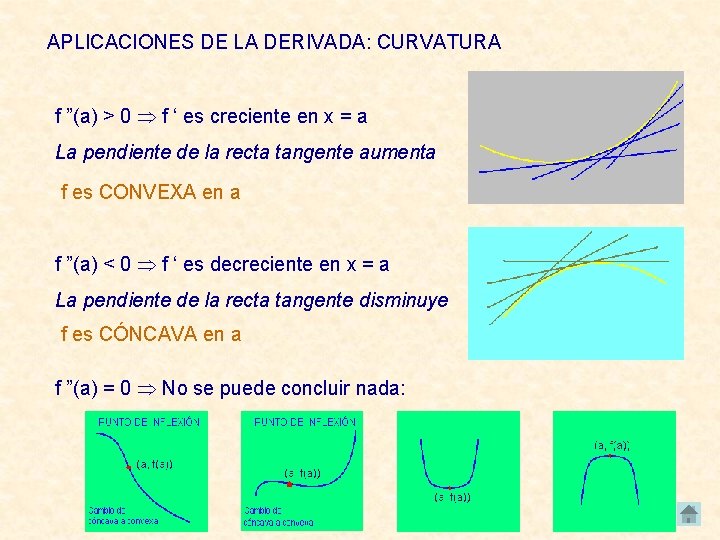
APLICACIONES DE LA DERIVADA: CURVATURA f ”(a) > 0 f ‘ es creciente en x = a La pendiente de la recta tangente aumenta f es CONVEXA en a f ”(a) < 0 f ‘ es decreciente en x = a La pendiente de la recta tangente disminuye f es CÓNCAVA en a f ”(a) = 0 No se puede concluir nada:

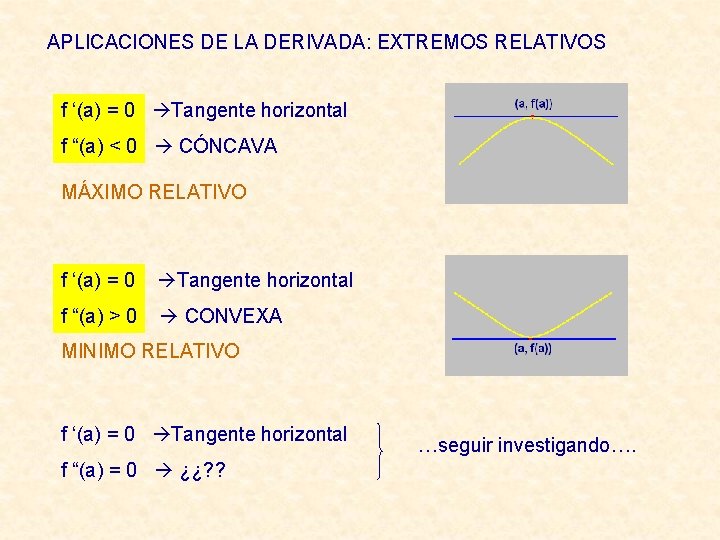
APLICACIONES DE LA DERIVADA: EXTREMOS RELATIVOS f ‘(a) = 0 Tangente horizontal f “(a) < 0 CÓNCAVA MÁXIMO RELATIVO f ‘(a) = 0 Tangente horizontal f “(a) > 0 CONVEXA MINIMO RELATIVO f ‘(a) = 0 Tangente horizontal f “(a) = 0 ¿¿? ? …seguir investigando….

OPTIMIZACIÓN REPRESENTACIÓN GRÁFICA DE FUNCIONES