TASA DE VARIACIN MEDIA Dada una funcin f

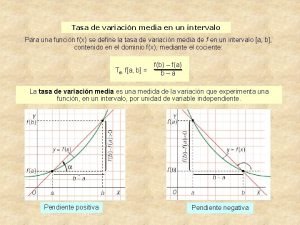
TASA DE VARIACIÓN MEDIA • Dada una función f definida en un intervalo [a, b], se llama TASA DE VARIACIÓN MEDIA de la función f en [ a, b ] al cociente: • • • f (b) - f(a) TVM = --------b-a • Como se observa en el valor de la TVM no influye el comportamiento de la función a lo largo del intervalo. Pueden existir diversas funciones que tengan la misma TVM en el mismo intervalo. • b–a • f(b) – f(a) es la variación o incremento de x, Δx. es la variación o incremento de f(x), Δf(x) o Δy. • TVM = Δy / Δx = m , pendiente del segmento que une los extremos de la función, o sea (a, f(a)) con (b, f(b)).

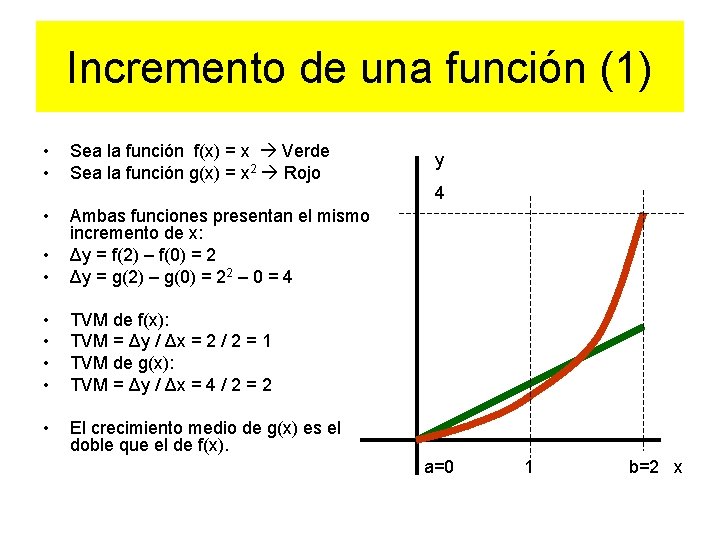
Incremento de una función (1) • • Sea la función f(x) = x Verde Sea la función g(x) = x 2 Rojo • • • Ambas funciones presentan el mismo incremento de x: Δy = f(2) – f(0) = 2 Δy = g(2) – g(0) = 22 – 0 = 4 • • TVM de f(x): TVM = Δy / Δx = 2 / 2 = 1 TVM de g(x): TVM = Δy / Δx = 4 / 2 = 2 • El crecimiento medio de g(x) es el doble que el de f(x). y 4 a=0 1 b=2 x

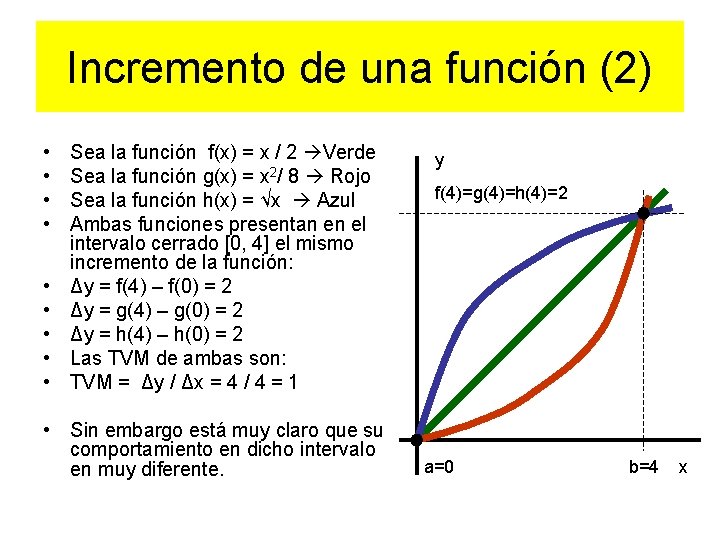
Incremento de una función (2) • • • Sea la función f(x) = x / 2 Verde Sea la función g(x) = x 2/ 8 Rojo Sea la función h(x) = √x Azul Ambas funciones presentan en el intervalo cerrado [0, 4] el mismo incremento de la función: Δy = f(4) – f(0) = 2 Δy = g(4) – g(0) = 2 Δy = h(4) – h(0) = 2 Las TVM de ambas son: TVM = Δy / Δx = 4 / 4 = 1 • Sin embargo está muy claro que su comportamiento en dicho intervalo en muy diferente. y f(4)=g(4)=h(4)=2 a=0 b=4 x

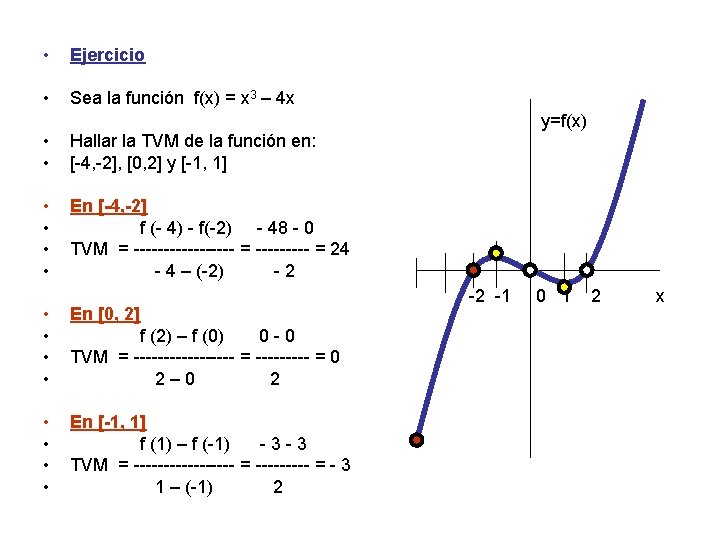
• Ejercicio • Sea la función f(x) = x 3 – 4 x y=f(x) • • Hallar la TVM de la función en: [-4, -2], [0, 2] y [-1, 1] • • En [-4, -2] f (- 4) - f(-2) - 48 - 0 TVM = --------- = 24 - 4 – (-2) -2 • • En [0, 2] f (2) – f (0) 0 -0 TVM = --------- = 0 2– 0 2 • • En [-1, 1] f (1) – f (-1) -3 -3 TVM = --------- = - 3 1 – (-1) 2 -2 -1 0 1 2 x

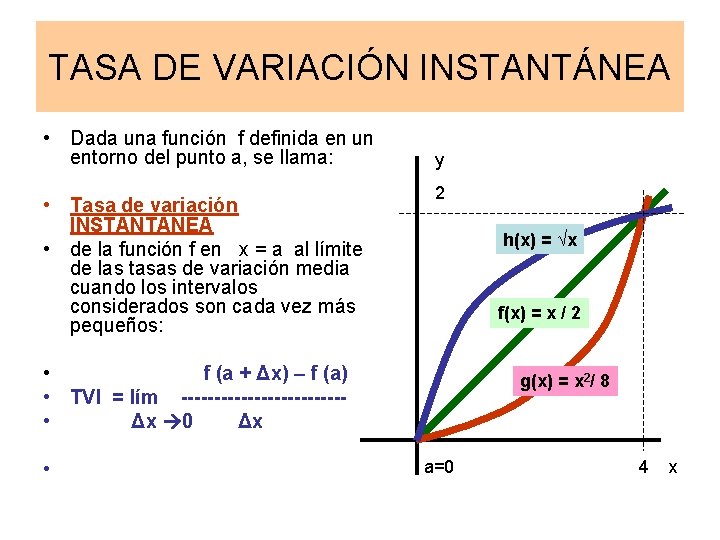
TASA DE VARIACIÓN INSTANTÁNEA • Dada una función f definida en un entorno del punto a, se llama: • Tasa de variación INSTANTÁNEA • de la función f en x = a al límite de las tasas de variación media cuando los intervalos considerados son cada vez más pequeños: y 2 h(x) = √x f(x) = x / 2 • f (a + Δx) – f (a) • TVI = lím ------------ • Δx 0 Δx • g(x) = x 2/ 8 a=0 4 x

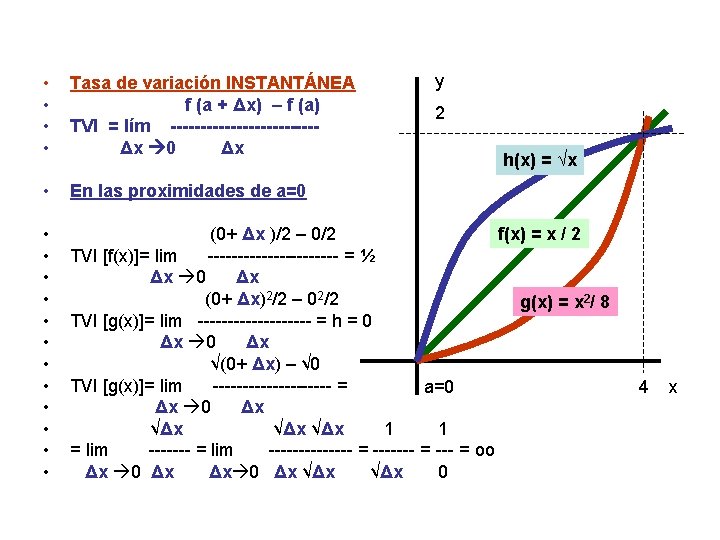
y • • Tasa de variación INSTANTÁNEA f (a + Δx) – f (a) TVI = lím ------------Δx 0 Δx • En las proximidades de a=0 • • • f(x) = x / 2 (0+ Δx )/2 – 0/2 TVI [f(x)]= lim ----------- = ½ Δx 0 Δx (0+ Δx)2/2 – 02/2 g(x) = x 2/ 8 TVI [g(x)]= lim ---------- = h = 0 Δx √(0+ Δx) – √ 0 TVI [g(x)]= lim ---------- = a=0 Δx √Δx √Δx 1 1 = lim -------------- = oo Δx 0 Δx √Δx 0 2 h(x) = √x 4 x

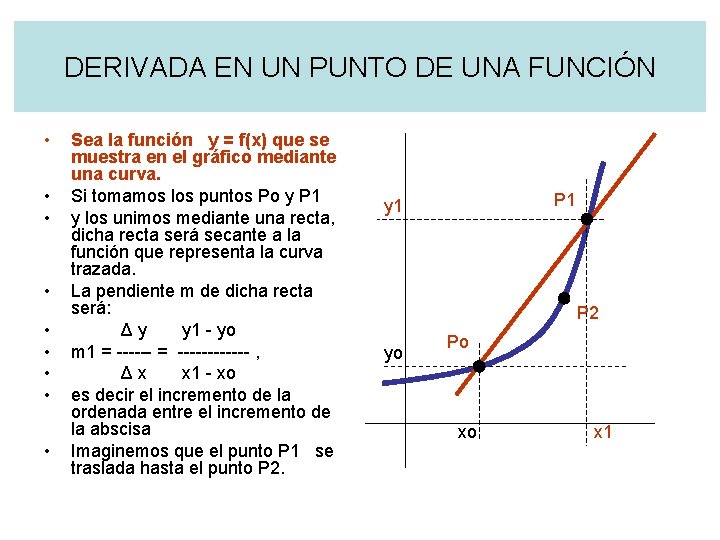
DERIVADA EN UN PUNTO DE UNA FUNCIÓN • • • Sea la función y = f(x) que se muestra en el gráfico mediante una curva. Si tomamos los puntos Po y P 1 y los unimos mediante una recta, dicha recta será secante a la función que representa la curva trazada. La pendiente m de dicha recta será: Δy y 1 - yo m 1 = ------------ , Δx x 1 - xo es decir el incremento de la ordenada entre el incremento de la abscisa Imaginemos que el punto P 1 se traslada hasta el punto P 2. P 1 y 1 P 2 yo Po xo x 1

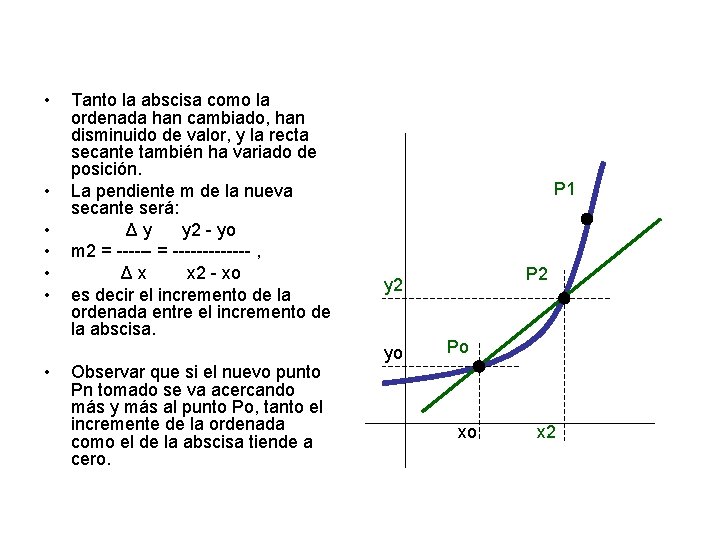
• • Tanto la abscisa como la ordenada han cambiado, han disminuido de valor, y la recta secante también ha variado de posición. La pendiente m de la nueva secante será: Δy y 2 - yo m 2 = ------------- , Δx x 2 - xo es decir el incremento de la ordenada entre el incremento de la abscisa. Observar que si el nuevo punto Pn tomado se va acercando más y más al punto Po, tanto el incremente de la ordenada como el de la abscisa tiende a cero. P 1 P 2 yo Po xo x 2

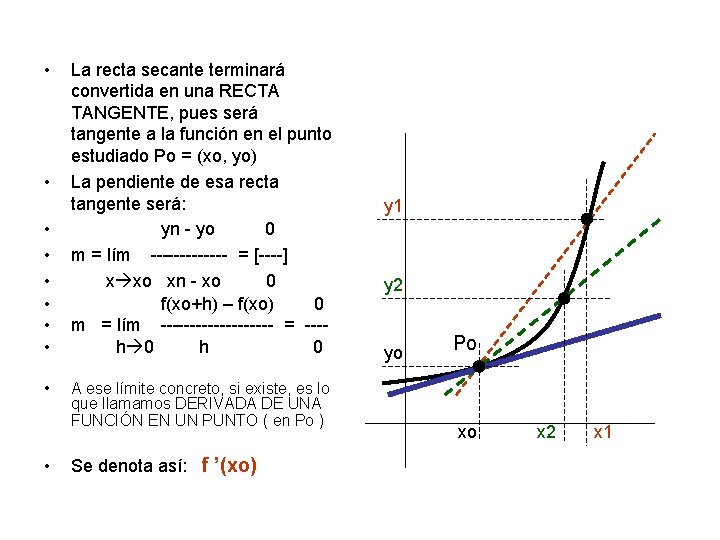
• • • La recta secante terminará convertida en una RECTA TANGENTE, pues será tangente a la función en el punto estudiado Po = (xo, yo) La pendiente de esa recta tangente será: yn - yo 0 m = lím ------- = [----] x xo xn - xo 0 f(xo+h) – f(xo) 0 m = lím ---------- = ---h 0 A ese límite concreto, si existe, es lo que llamamos DERIVADA DE UNA FUNCIÓN EN UN PUNTO ( en Po ) Se denota así: f ’(xo) y 1 y 2 yo Po xo x 2 x 1

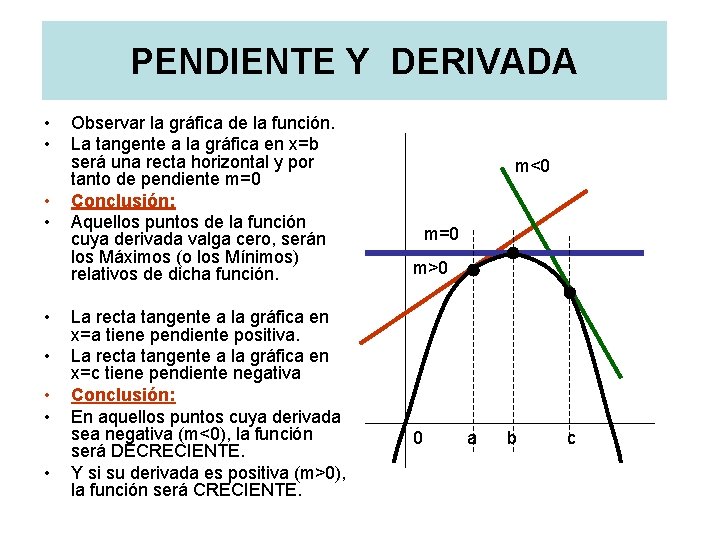
PENDIENTE Y DERIVADA • • • Observar la gráfica de la función. La tangente a la gráfica en x=b será una recta horizontal y por tanto de pendiente m=0 Conclusión: Aquellos puntos de la función cuya derivada valga cero, serán los Máximos (o los Mínimos) relativos de dicha función. La recta tangente a la gráfica en x=a tiene pendiente positiva. La recta tangente a la gráfica en x=c tiene pendiente negativa Conclusión: En aquellos puntos cuya derivada sea negativa (m<0), la función será DECRECIENTE. Y si su derivada es positiva (m>0), la función será CRECIENTE. m<0 m=0 m>0 0 a b c

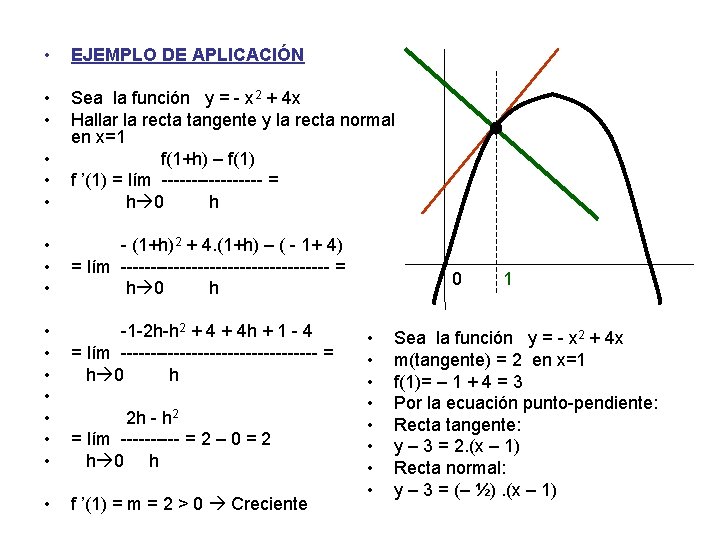
• EJEMPLO DE APLICACIÓN • • • Sea la función y = - x 2 + 4 x Hallar la recta tangente y la recta normal en x=1 f(1+h) – f(1) f ’(1) = lím --------- = h 0 h • • • - (1+h)2 + 4. (1+h) – ( - 1+ 4) = lím ------------------ = h 0 h • • -1 -2 h-h 2 + 4 h + 1 - 4 = lím ----------------- = h 0 h • f ’(1) = m = 2 > 0 Creciente 2 h - h 2 = lím ----- = 2 – 0 = 2 h 0 • • 1 Sea la función y = - x 2 + 4 x m(tangente) = 2 en x=1 f(1)= – 1 + 4 = 3 Por la ecuación punto-pendiente: Recta tangente: y – 3 = 2. (x – 1) Recta normal: y – 3 = (– ½). (x – 1)

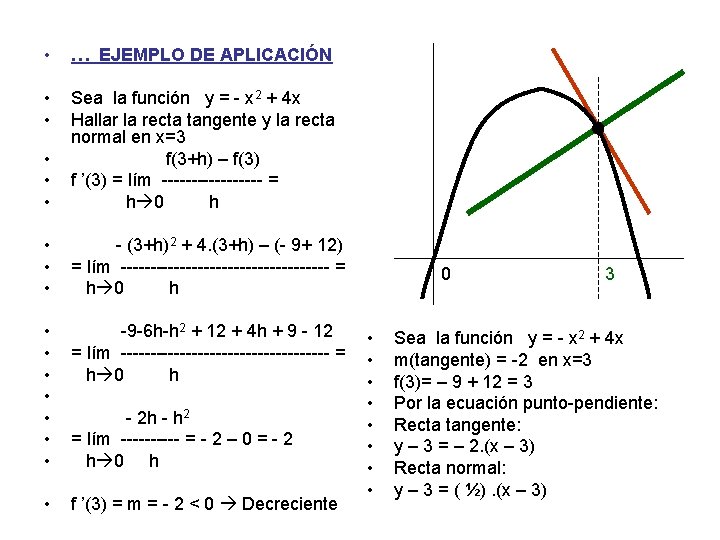
• … EJEMPLO DE APLICACIÓN • • • Sea la función y = - x 2 + 4 x Hallar la recta tangente y la recta normal en x=3 f(3+h) – f(3) f ’(3) = lím --------- = h 0 h • • • - (3+h)2 + 4. (3+h) – (- 9+ 12) = lím ------------------ = h 0 h • • -9 -6 h-h 2 + 12 + 4 h + 9 - 12 = lím ------------------ = h 0 h • f ’(3) = m = - 2 < 0 Decreciente - 2 h - h 2 = lím ----- = - 2 – 0 = - 2 h 0 • • 3 Sea la función y = - x 2 + 4 x m(tangente) = -2 en x=3 f(3)= – 9 + 12 = 3 Por la ecuación punto-pendiente: Recta tangente: y – 3 = – 2. (x – 3) Recta normal: y – 3 = ( ½). (x – 3)

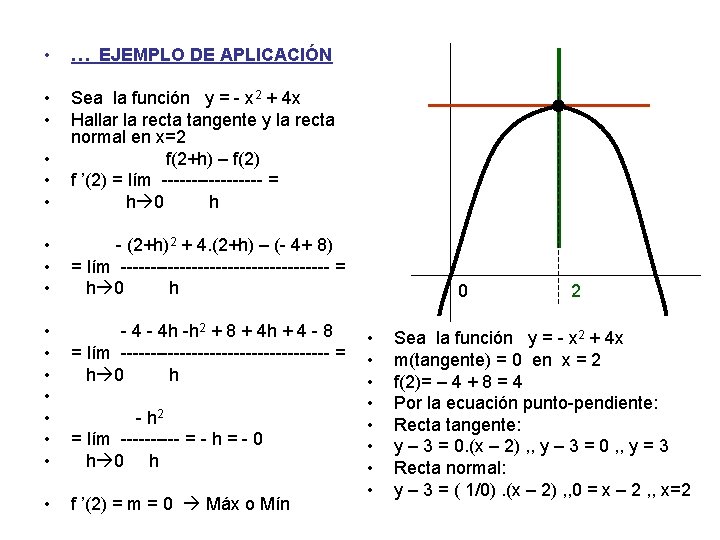
• … EJEMPLO DE APLICACIÓN • • • Sea la función y = - x 2 + 4 x Hallar la recta tangente y la recta normal en x=2 f(2+h) – f(2) f ’(2) = lím --------- = h 0 h • • • - (2+h)2 + 4. (2+h) – (- 4+ 8) = lím ------------------ = h 0 h • • - 4 h -h 2 + 8 + 4 h + 4 - 8 = lím ------------------ = h 0 h • f ’(2) = m = 0 Máx o Mín - h 2 = lím ----- = - h = - 0 h 0 • • 2 Sea la función y = - x 2 + 4 x m(tangente) = 0 en x = 2 f(2)= – 4 + 8 = 4 Por la ecuación punto-pendiente: Recta tangente: y – 3 = 0. (x – 2) , , y – 3 = 0 , , y = 3 Recta normal: y – 3 = ( 1/0). (x – 2) , , 0 = x – 2 , , x=2