A LINGUAGEM DOS NMEROS Os conjuntos numricos q

A LINGUAGEM DOS NÚMEROS

Os conjuntos numéricos q Como surgiram os números? Eles foram sendo criados pouco a pouco. A cada nova dificuldade ou necessidade, o homem e a ciência foram juntando novos tipos de números aos já existentes. q Com o tempo, por questões práticas, foi preciso agrupá-los, formando estruturas com características e propriedades comuns.

Conjuntos – Conceitos iniciais q Ficaram definidos, assim, os conjuntos numéricos ü ℕ, dos números naturais; ü ℤ, dos números inteiros; ü ℚ, dos números racionais; ü ℝ, dos números reais; ü ℂ, dos números complexos.

Conjunto dos números naturais (ℕ) q A necessidade de contar surgiu com o início da civilização dos povos. Povos primitivos contavam apenas um, dois e muitos. Esses três conceitos, sozinhos, já resolviam seus problemas. Depois outras quantidades (três, quatro, etc. ) foram sendo incorporadas. A idéia do zero só surgiu mais tarde. q Números utilizados para contar formam o conjunto ℕ dos números naturais, definido assim: ℕ = {0, 1, 2, 3, 4, 5, . . . }

Conjunto dos números inteiros (ℤ) q A soma e o produto de dois naturais são sempre naturais. Mas a diferença de dois naturais nem sempre é natural. Por exemplo, (5 – 2) ℕ, mas (2 – 5) ℕ q Subtrações como essa última só são definidas com a introdução dos números inteiros negativos (– 1, – 2, – 3, – 4, . . . ). q A união dos naturais com os inteiros negativos forma o conjunto ℤ dos números inteiros. ℤ = {. . . , – 3, – 2, – 1, 0, 1, 2, 3, . . . }

Conjunto dos números inteiros (ℤ) q Podemos separar os inteiros em três categorias: ü Os positivos: 1, 2, 3, 4, . . . ü O zero: 0 ü Os negativos: – 1, – 2, – 3, – 4, . . . Ø De maneira geral, se k é um número inteiro, o número –k também é inteiro. Ø Dizemos que k e –k são simétricos ou opostos.

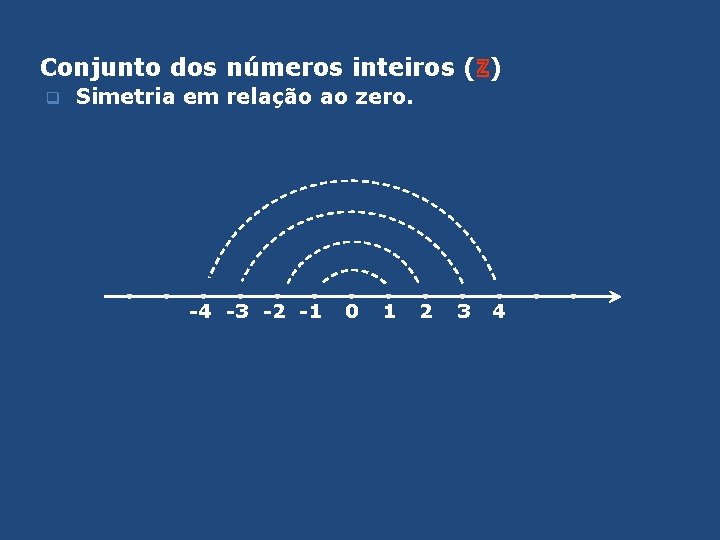
Conjunto dos números inteiros (ℤ) q Simetria em relação ao zero. -4 -3 -2 -1 0 1 2 3 4

Exemplo De dois inteiros simétricos k e –k, não-nulos, qual é o positivo? Qual o negativo? Dois inteiros simétricos podem ser iguais? A soma, a diferença, o produto e o quociente de dois inteiros são sempre inteiros?

Conjunto dos números inteiros (ℤ) q Definem-se, em ℤ, as relações de igualdade e de ordem (desigualdade). q Se p e q são dois inteiros, eles satisfazem uma, e somente uma, das seguintes relações: ü p = q (p é igual a q); → 3– 5=2 ü p < q (p é menor que q); → – 5 < – 1 < 0 < 3 ü p > q (p é maior que q). → 7 > 2 > 0 > – 4

Observação q Certos subconjuntos de ℕ e ℤ são definidos por meio de desigualdades. No caso, devemos estar atentos ao universo indicado. q Exemplos Ø A = {x ℕ / x < 4} → A = {0, 1, 2, 3}. Ø B = {x ℤ / – 3 ≤ x < 2} → B = {– 3, – 2, – 1, 0, 1}. Ø C = {x ℤ / x ≥ – 2} → C = {– 2, – 1, 0, 1, . . . }.

Observação q Os conjuntos numéricos podem vir acompanhados de certos símbolos, que têm a função de excluir, dele, determinados números. Veja: Ø O símbolo asterisco (*) exclui o zero; Ø O símbolo mais (+) exclui os negativos; Ø O símbolo menos (–) exclui os positivos.

Observação q Quando colocamos os inteiros em ordem crescente, valem os conceitos de antecessor e sucessor. O antecessor de 8 é o 7 e o sucessor de 8 é o 9. Identifique, entre as sentenças a seguir, as que são verdadeiras. ü O antecessor de – 6 é – 5 ( ). ü Se p é inteiro, seu sucessor é (p + 1) e seu antecessor (p – 1) ( ). ü Se p, é par e q ímpar, então (p + 1). q é impar ( ). ü Se p é par e q é ímpar, então (p + q). (q + 1) é par ( ). ü No conjunto dos naturais, 0 não tem antecessor ( ).

Conjunto dos números racionais (ℚ) q A necessidade de operar com grandezas que nem sempre podem ser representadas por números inteiros e, consequentemente exigem subdivisões levou à criação dos números fracionários: 3 5 , 8 7 , 1 10 , etc. Ø Divisões como essas são definidas com a introdução do conceito de número racional.

Conjunto dos números racionais (ℚ) q Todo quociente p/q da divisão de um inteiro p por um inteiro q (q ≠ 0) é chamado de número racional. q Veja a definição do conjunto ℚ dos números racionais. ℚ = {x/x = p/q; p, q ℤ, q ≠ 0}

Exemplo São racionais os seguintes números 8 2 =4 3 ü (fracionário de termos inteiros) 7 – 3 8 5 9 ü (inteiro) = – 0, 375 ü (decimal exato) = 0, 555. . . ü (dízima periódica)

Conjunto dos números racionais (ℚ) q Em resumo, são números racionais ü Os números inteiros; ü Os números fracionários; ü Os decimais exatos; ü As dízimas periódicas.

Transformando decimais exatos em frações q Um número decimal exato é sempre igual a uma fração, cujo denominador é uma potência de base 10 e expoente natural. q Exemplos 7 35 35 = 0, 35 = = 2 20 10 100 – 1, 8 = – 9 – 18 = = 5 101 10

Transformando decimais periódicos em frações q Numa dízima periódica, o grupo de algarismos que se repete é chamado período da dízima. Por exemplo na dízima 23, 4727272. . . , o período é 72. q A fração que dá origem a uma dízima é a sua geratriz.

Exemplos Achar a fração geratriz da dízima periódica 0, 424242. . . Suponhamos x = 0, 424242. . . (1) ⇒ 100. x = 100. 0, 424242. . . ⇒ 100 x = 42, 4242. . . (2) subtraindo (2) – (1), membro a membro 100 x = 42, 4242. . . – x= 0, 424242. . . 99 x = 42 14 42 = ⇒ x= 33 99

Exemplos Encontrar a 4, 73333. . . Suponhamos fração geratriz x = 4, 73333. . . da dízima periódica (1) ⇒ 10. x = 10. 4, 73333. . . ⇒ 10 x = 47, 3333. . . (2) subtraindo (2) – (1), membro a membro 10 x = 47, 33333. . . – x= 4, 73333. . . 9 x = 42, 6 ⇒ 90 x = 426 ⇒ x= 426 90 = 71 15

Conjunto dos números racionais (ℚ) q Podemos representar os números racionais por pontos pertencentes a uma reta orientada, bastando para isso fazer subdivisões convenientes no eixo dos inteiros. – 5/3 – 6/5 -3 -2 -1 0, 333. . . 0 1, 5 1 0, 6 2 3

Conjunto dos números reais (ℝ) q Vimos anteriormente, que os únicos números decimais racionais são os exatos e as dízimas periódicas. q Existirão números decimais que não sejam exatos nem dízimas? Ou seja, números decimais nãoracionais?

Conjunto dos números reais (ℝ) q Veja a figura a seguir. Ela mostra um triângulo retângulo cujos catetos medem 1 unidade. Veja o cálculo de sua hipotenusa. x 1 x 2 = 1 2 + 1 2 x 2 = 2 x = √ 2 1 ü Extraindo a raiz quadrada de 2 nos levará ao número 1, 41421356237. . . que não é racional.

Conjunto dos números reais (ℝ) q Números com √ 2 são chamados de números irracionais. Sua representação decimal não é exata e nem periódica. q De modo geral, número irracional é todo número que, escrito na forma decimal, é infinito e nãoperiódico. Veja alguns exemplos: ü √ 3 = 1, 73205080. . . ü 3 √ 5 = 1, 70099759. . . ü = 3, 141592653. . . ü 0, 202202220. . .

Você sabia? que é aproximadamente 3, 141592653589793238462643383279502884197169 399375105820974944592307816406286208998628 034825342117067982148086513282306647093844 609550582231725359408128481117450284102701 938521105559644622948954930381964428810975 665933446128475648233786783165271201909145 648566923460348610454326648213393607260249 1412737245870066…? �

Conjunto dos números reais (ℝ) q A reunião dos racionais com os irracionais resulta no conjunto dos números reais. Ele é a partir de agora, o nosso universo numérico. ℝ = {x/x é racional ou irracional}

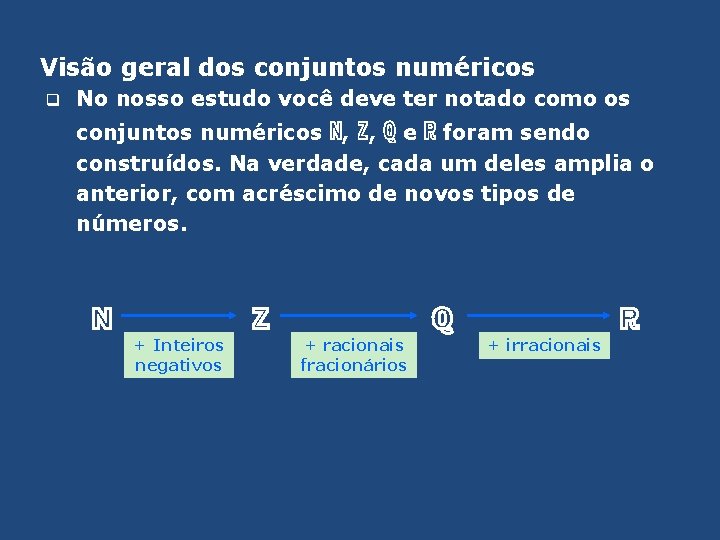
Visão geral dos conjuntos numéricos q No nosso estudo você deve ter notado como os conjuntos numéricos ℕ, ℤ, ℚ e ℝ foram sendo construídos. Na verdade, cada um deles amplia o anterior, com acréscimo de novos tipos de números. ℕ ℤ + Inteiros negativos ℚ + racionais fracionários ℝ + irracionais

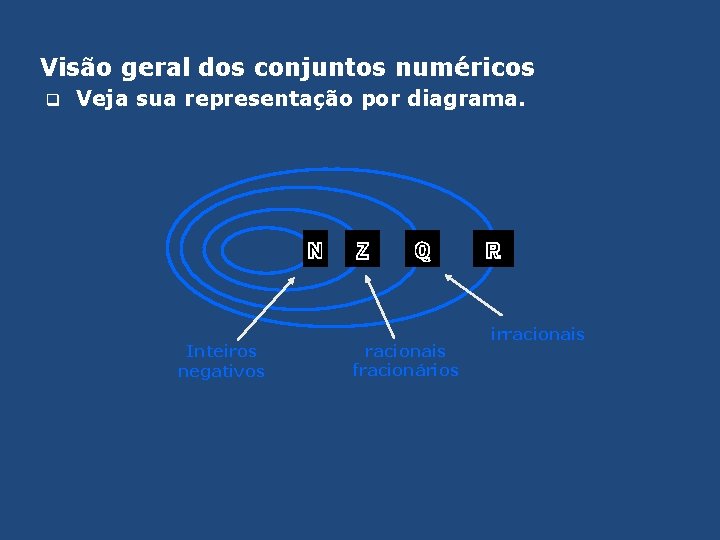
Visão geral dos conjuntos numéricos q Veja sua representação por diagrama. ℕ Inteiros negativos ℤ ℚ racionais fracionários ℝ irracionais

Números reais como pontos da reta q O conjunto ℝ dos números reais pode ser colocado em correspondência com o conjunto dos pontos de uma reta. Para isso definimos ü Um sentido positivo, indicado pela seta; ü Um ponto O, chamado origem, associado ao zero; ü uma unidade de medida arbitrária. O 1 u ü A esta reta, damos o nome de reta real ou eixo real;

Números reais como pontos da reta q Na reta da figura marcamos os pontos O(0), A(1), B(– 3, 5), C(4) e D(– 2). B – 3, 5 D O A C – 2 0 1 4 ü Na representação: A(1), 1 é a abscissa ou a coordenada do ponto A; ü Em geral: Escrevemos P(x) para indicar que o ponto P está associado ao número x.

Números reais como pontos da reta q A reta estabelece uma ordenação para os números reais, expressas por relações de desigualdade. Sendo a e b dois reais distintos, temos: ü a < b (a é menor que b) significa que, na reta real, a está à esquerda de b. ü a > b (a é maior que b) significa que, na reta real, a está à direita de b.

Números reais como pontos da reta q Na reta real da figura a seguir, estão representados os números reais 0, p e q. O p 0 q Podemos escrever, por exemplo: üp<0 (p é negativo) üq>0 (q é positivo) üp<0<q (0 está entre p e q)

Observação q A relação a ≤ b significa que (a < b ou a = b) e a relação a ≥ b indica que (a > b ou a = b). ü a ≤ b (a é menor que ou igual a b) ü a ≥ b (a é maior que ou igual a b) q Exemplos ü 5≥ 3 (5 é maior ou igual a 3) ü – 2 ≤ 1 (– 2 é menor ou igual a 1)

Exemplos q A figura mostra a reta real, em que O é a origem. São dados os pontos A(a) e B(b) e sabe-se que OA = OC. A O C B a b a) Quais são as abscissas de dos pontos O e C. 0 e –a b) Complete os pontilhados desigualdade > ou <. com os sinais de < 0 a. . > 0 –a. . > 0 a + b. . > 0 a 2. . > 0 b. . < 0 –b. . < 0 ab. . < a –b. .

INTERVALOS REAIS

Intervalos reais q Considere os conjuntos A = {x ℤ /– 3 ≤ x < 2} e B = {x ℝ /– 3 ≤ x < 2}. É verdade que A = B? ü O conjunto A tem apenas os elementos – 3, – 2, – 1, 0 e 1, enquanto o conjunto B tem infinitos elementos, dentre os quais estão os elementos de A. ü O conjunto A pode ter seus elementos representados na reta real, delimitando-se uma parte dessa reta. veja – 3 2

Intervalos reais q Muitas vezes trabalhamos com determinados subconjuntos de ℝ (partes da reta), denominados intervalos reais. Em geral eles são definidos por desigualdades. ü Suponhamos dois números reais a e b tais que a < b. Os subconjuntos de ℝ definidos a seguir são chamados de intervalos reais de extremos a e b.

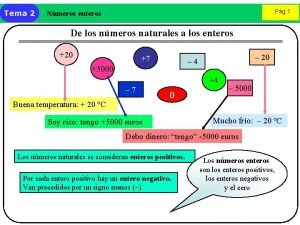
Intervalos reais – limitados q Intervalo fechado a, b. ü Representações: [a, b] = {x Na reta real: a ℝ /a ≤ x ≤ b} b q Intervalo aberto a, b. ü Representações: Na reta real: ]a, b[ = {x a ℝ /a < x < b} b

Intervalos reais – limitados q Intervalo fechado em a e aberto em b. ü Representações: Na reta real: [a, b[ = {x ℝ /a ≤ x < b} a b q Intervalo aberto em a e fechado em b. ü Representações: Na reta real: ]a, b] = {x a ℝ /a < x ≤ b} b

Observação q Observe que cada intervalo inclui todos os reais entre a e b; para os extremos a e b, temos: ü inclusão do extremo fechado bolinha cheia ( • ) colchetes normais [ ]. ü exclusão do extremo aberto bolinha vazia (o) colchetes invertidos ] [.

Intervalos reais – ilimitados q Intervalo de a fechado até +. ü Representações: Na reta real: [a, + [ = {x ℝ / x ≥ a} a q Intervalo de a aberto até +. ü Representações: Na reta real: ]a, + [ = {x a ℝ /x > a}

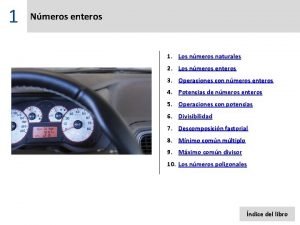
Intervalos reais – ilimitados q Intervalo de – até a fechado. ü Representações: ]– , a] = {x Na reta real: ℝ / x ≤ a} a q Intervalo de – até a aberto. ü Representações: Na reta real: ]– , a[ = {x ℝ /x < a} a

Exemplos q Vamos analisar, em detalhes, o intervalo real A = [– 3, 5[. ü Temos um intervalo fechado em – 3 e aberto em 5; ü Representa todos os reais entre – 3 e 5; ü Inclui o extremo – 3 e exclui o extremo 5. A = {x ℝ / – 3 ≤ x < 5} – 3 5 Note que: – 3 A; 4, 99 A; 5 A

Exemplos q Vamos analisar, agora, o intervalo B, representado na reta real. 2 ü temos um intervalo aberto de 2 a + ; ü estão indicados todos os reais maiores que 2; ü o extremo 2 está excluído; B = {x ℝ / x > 2} Note que: 0 B; 2, 001 B; 1035 B

OPERAÇÕES COM INTERVALOS REAIS

Operando com intervalos reais q Podemos efetuar, com intervalos, as operações usuais com conjuntos. ü A B A interseção B: conjunto dos elementos comuns a A e B; ü A B A união B: conjunto dos elementos que pertencem a pelo menos um dos conjuntos A ou B; ü A – B A menos B: conjunto dos elementos que pertencem a A e não pertencem a B. Ø Na prática, operações que envolvem intervalos são efetuadas a partir da representação na reta real.

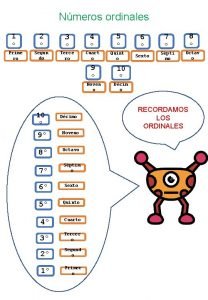
Exemplo q Dado os intervalos A = ]– 2, 5] e B = ]3, + [, obter A B, A B e A – B. ü Cálculo de A B. 5 – 2 B = ]3, + [ 3 3 A = ]– 2, 5] 5 A ⋂ B = ]3, 5]

Exemplo q Dado os intervalos A = ]– 2, 5] e B = ]3, + [, obter A B, A B e A – B. ü Cálculo de A B. 5 – 2 3 – 2 A = ]– 2, 5] B = ]3, + [ A B = ]– 2, + [

Exemplo q Dado os intervalos A = ]– 2, 5] e B = ]3, + [, obter A B, A B e A – B. ü Cálculo de A – B. 5 – 2 3 A = ]– 2, 5] B = ]3, + [ A ⋂ B = ]– 2, 3]

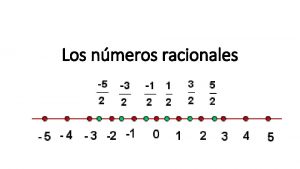
Exemplos q Complete o quadro abaixo. intervalo Representação na reta ]– , 5] ]– 5, 2] 5 – 5 ]– 1, + [ [– 7, 4[ [3, + [ – 2 {x ℝ; x ≤ 5} {x ℝ; – 5 < x ≤ 2} 2 {x ℝ; x > – 1} – 1 [– 2, ½] Subconjunto de ℝ {x ℝ; – 2 ≤ x ≤ ½} ½ – 7 4 3 {x ℝ; – 7 ≤ x < 4} {x ℝ; x ≥ 3}

Exemplos q Chama-se amplitude de um intervalo real limitado e fechado a medida de seu comprimento na reta real, ou ainda, a distância entre seus extremos. a) Qual é a amplitude dos intervalos [2, 5] e [– 3, 4]? 3 e 7 b) Sendo a e b reais, com a < b, qual é a amplitude dobintervalo [a, b]? –a c) Escreva todos os intervalos fechados amplitude sendo [– 5, – 1] e 4, [– 1, 3] – 1 um de seus extremos. de

Exemplos q Escreva dois intervalos A e B, limitados, aos quais pertença o real e não pertençam os reais 3 e 4. Escreva, também, um intervalo limitado C, de amplitude 1, 5 e ao qual pertençam dois números primos. A = ]3, ] C = [2; 3, 5] e B = [ , 4[