NMEROS REAIS PROFESSOR CLBER BORGES NMEROS IRRACIONAIS Os

NÚMEROS REAIS PROFESSOR CLÉBER BORGES

NÚMEROS IRRACIONAIS Os Números Irracionais são números decimais, infinitos e não-periódicos e não podem ser representados por meio de frações irredutíveis. Interessante notar que a descoberta dos números irracionais foi considerada um marco nos estudos da geometria. Isso porque preencheu lacunas, como por exemplo, a medida da diagonal de um quadrado de lado igual a 1.

NÚMEROS IRRACIONAIS Como a diagonal divide o quadrado em dois triângulos retângulos, podemos calcular essa medida usando o Teorema de Pitágoras

NÚMEROS IRRACIONAIS Com vimos, a medida da diagonal desse quadrado será √ 2. O problema é que o resultado desta raiz é um número decimal infinito e não periódico. Por mais que tentemos encontrar um valor exato, só conseguimos aproximações deste valor. Considerando 12 casas decimais essa raiz pode ser escrita como: √ 2 = 1, 414213562373. . Alguns exemplos de irracionais: √ 3 = 1, 732050807568. . √ 5 = 2, 236067977499. . . √ 7 = 2, 645751311064. . .

NÚMEROS IRRACIONAIS E DÍZIMAS PERIÓDICAS

CLASSIFICAÇÃO DOS NÚMEROS IRRACIONAIS Os números irracionais podem ser algébricos ou transcendentes. Será algébrico quando satisfaz uma equação algébrica de coeficientes inteiros, se não for algébrico, então será transcendente. Por exemplo, a raiz quadrada de 2 (√ 2) pode ser escrita como sendo x 2 - 2 = 0, então é irracional algébrico. O número pi (π) é o mais famoso dos números irracionais transcendentes. Seu valor é π = 3, 14159265358979323846… e representa a proporção da medida da circunferência e do seu diâmetro. Um outro exemplo de irracional transcendente é o número de Neper, representado por e, sendo aproximadamente igual a 2, 718281. Podemos ainda citar o número de ouro, representado por Phi (ϕ). Seu valor é ϕ = 1, 618033. . . O número de ouro é encontrado a partir da razão áurea ou divina proporção, sendo encontrada em muitos elementos da natureza. Além disso, esta razão está presente em diversas pinturas, esculturas e construções.

VÍDEO Veja na animação abaixo e entenda como o número de ouro está presente em nosso cotidiano.

CONJUNTOS NUMÉRICOS O conjunto dos números irracionais é representado por I. Da união deste conjunto com o conjunto dos números racionais (Q) temos o conjunto dos números reais (R). O conjunto dos números irracionais possui infinitos elementos, sendo que existem mais irracionais do que racionais.

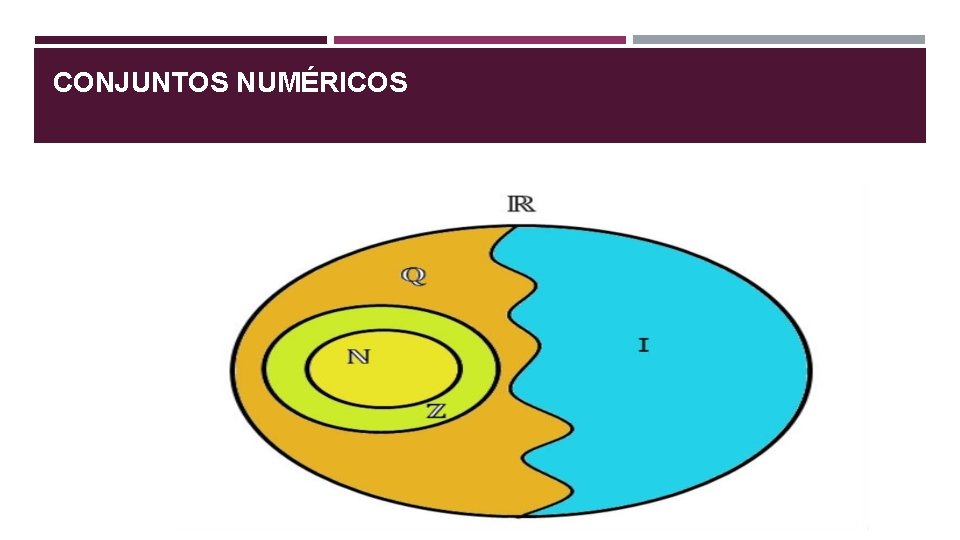
CONJUNTOS NUMÉRICOS

EXERCÍCIOS RESOLVIDOS 1) UEL - 2003 Observe os seguintes números. I. 2, 212121. . . II. 3, 212223. . . III. π/5 IV. 3, 1416 V. √- 4 Assinale a alternativa que identifica os números irracionais. a) I e II b) I e IV c) II e III d) II e V e) III e V

EXERCÍCIOS RESOLVIDOS 2) Fuvest - 2014 O número real x, que satisfaz 3 < x < 4, tem uma expansão decimal na qual os 999 primeiros dígitos à direita da vírgula são iguais a 3. Os 1. 000. 001 dígitos seguintes são iguais a 2 e os restantes são iguais a zero. Considere as seguintes afirmações: I. x é irracional. II. x ≥ 10/3 III. x. 102 000 é um inteiro par. Então: a) nenhuma das três afirmações é verdadeira. b) apenas as afirmações I e II são verdadeiras. c) apenas a afirmação I é verdadeira. d) apenas a afirmação II é verdadeira. e) apenas a afirmação III é verdadeira.

EXERCÍCIOS RESOLVIDOS 3) UFSM - 2003 Assinale verdadeira (V) ou falsa (F) em cada uma das afirmações a seguir. ( ) A letra grega π representa o número racional que vale 3, 14159265. ( ) O conjunto dos números racionais e o conjunto dos números irracionais são subconjuntos dos números reais e possuem apenas um ponto em comum. ( ) Toda dízima periódica provém da divisão de dois números inteiros, portanto é um número racional. A sequência correta é a) F - V b) V - F c) V - F - V d) F - V e) F - V - F