Para um melhor entendimento da matemtica e das

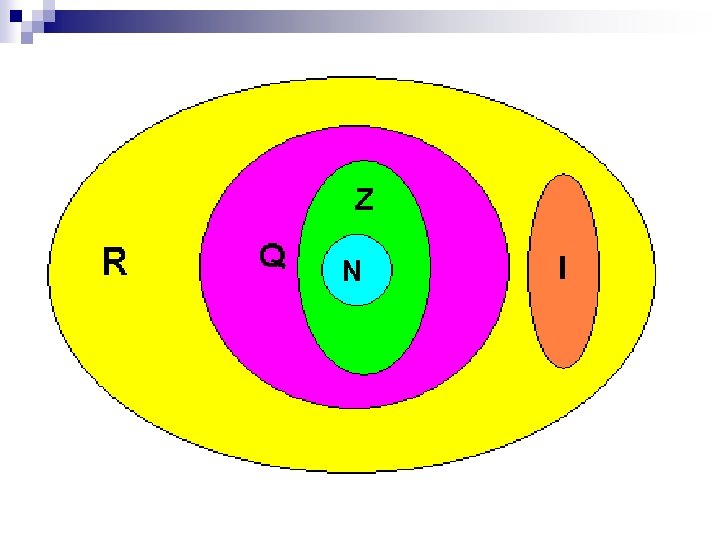
Para um melhor entendimento da matemática e das propriedades que a envolve, os números foram agrupados em alguns conjuntos, e cada conjunto tem certas propriedades. . . Conheça-os:

É AQUELE QUE CONTÉM OS NÚMEROS QUE VOCÊ APRENDEU A CONTAR NATURALMENTE; n É REPRESENTADO PELA LETRA N. ; n É INFINITO. n

CADA NÚMERO SITUADO À DIREITA O ZERO ÉO DO OUTRO REPRESENTA UMA QUANTIDADE MAIOR, ÚNICO NÚMERO n ESSE NÚMERO É CHAMADO NATURAL QUE SUCESSOR, NÃO É SUCESSOR n CADA NÚMERO SITUADO À ESQUERDA DE NENHUM DO OUTRO REPRESENTA UMA OUTRO QUANTIDADE MENOR, n ESSE NÚMERO É CHAMADO ANTECESSOR, n

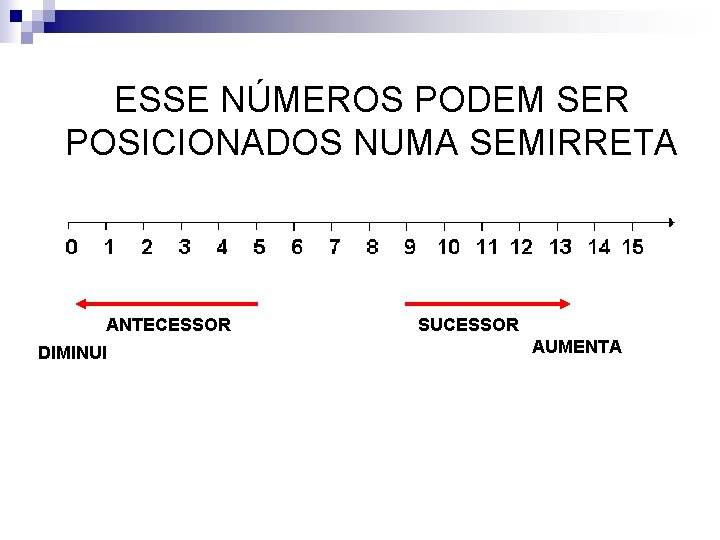
ESSE NÚMEROS PODEM SER POSICIONADOS NUMA SEMIRRETA ANTECESSOR DIMINUI SUCESSOR AUMENTA

CITAMOS COMO SUBCONJUNTOS DE N: n N*= {1, 2, 3, 4, 5, 6, . . . } n PARES = {0, 2, 4, 6, 8, 10, 12, . . . } n ÍMPARES= {1, 3, 5, 7, 9, 11, 13, 15, . . . } Apresentação de expressões numéricas

ENVOLVE OS NÚMEROS POSITIVOS E NEGATIVOS; n COMO O PRÓPRIO NOME DIZ, SEUS NÚMEROS SÃO INTEIROS; n É REPRESENTADO PELA LETRA Z. n

n ELE É INFINITO; O NÚMERO SITUADO À DIREITA É MAIOR QUE O DA ESQUERDA n O NÚMERO SITUADO À ESQUERDA É MENOR QUE O DA DIREITA n n HÁ UMA SIMETRIA EM RELAÇÃO AO ZERO. O OPOSTO OU SIMÉTRICO DE 3 É -3, VALENDO 3+ (-3) =0

ESSE NÚMEROS PODEM SER POSICIONADOS NUMA RETA NEGATIVOS DIMINUI POSITIVOS PERCEBA QUE OS NÚMEROS POSITIVOS SÃO OS NÚMEROS NATURAIS AUMENTA

CITAMOS COMO SUBCONJUNTOS DE Z: Z*= {. . . , -3, -2, -1, 1, 2, 3, 4, 5, 6, . . . } n Z+ = {0, 1, 2, 3, 4, 5, 6, . . . } n Z- = {. . . , -6, -5, -4, -3, -2, -1, 0} n O ZERO É NEUTRO, UMA VEZ QUE SOMADO À ALGUM NÚMERO OU SUBTRAIDO, ESSE NÚMERO NÃO SE ALTERA PERCEBA QUE Z+ = N Apresentação de expressões numéricas

AO ACRESCENTARMOS AS FRAÇÕES NÃO APARENTES POSITIVAS E NEGATIVAS AO CONJUNTO DOS NÚMEROS INTEIROS TEMOS O CONJUNTO DOS NÚMEROS RACIONAIS. É REPRESENTADO PELA LETRA Q (QUOCIENTE DA DIVISÃO).

FRAÇÃO APARENTE É AQUELA QUE INDICA UM NÚMERO INTEIRO TODO NÚMERO INTEIRO PODE SER ESCRITO NA FORMA SÃO RACIONAIS:

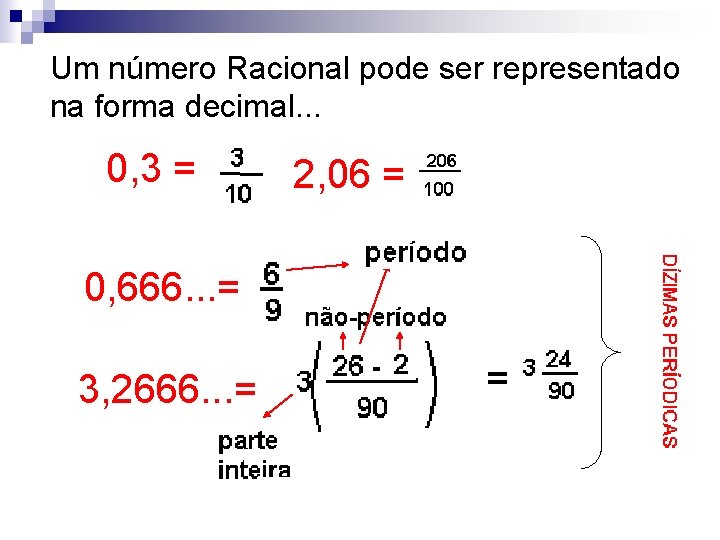
Um número Racional pode ser representado na forma decimal. . . 0, 3 = 2, 06 = 0, 666. . . = 3, 2666. . . = =

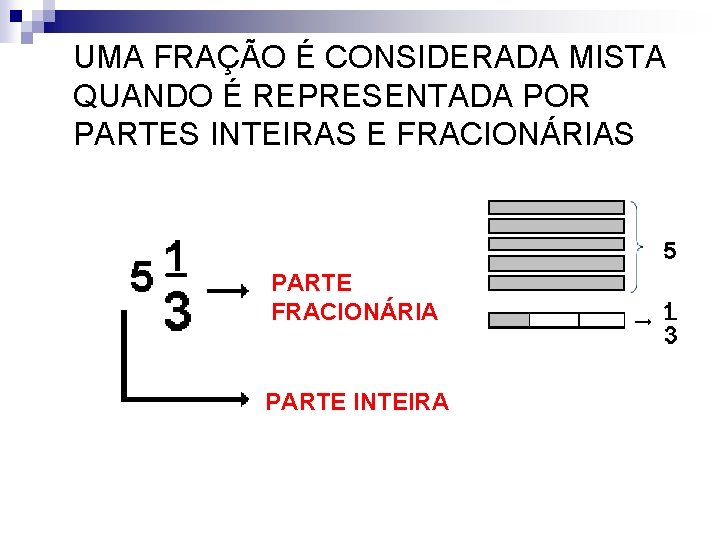
UMA FRAÇÃO É CONSIDERADA MISTA QUANDO É REPRESENTADA POR PARTES INTEIRAS E FRACIONÁRIAS PARTE FRACIONÁRIA PARTE INTEIRA

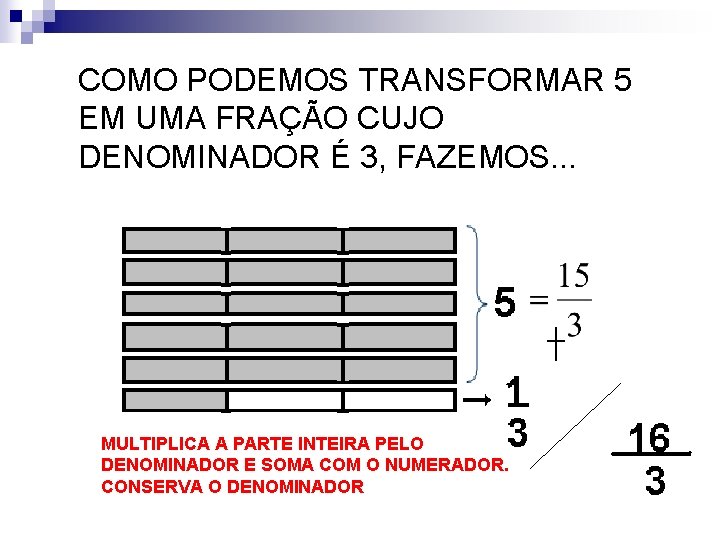
COMO PODEMOS TRANSFORMAR 5 EM UMA FRAÇÃO CUJO DENOMINADOR É 3, FAZEMOS. . . MULTIPLICA A PARTE INTEIRA PELO DENOMINADOR E SOMA COM O NUMERADOR. CONSERVA O DENOMINADOR

OBSERVAÇÕES: n ENTRE DOIS NÚMEROS INTEIROS NEM SEMPRE EXISTE UM NÚMERO INTEIRO n. ENTRE DOIS NÚMEROS RACIONAIS SEMPRE EXISTE OUTRO NÚMERO RACIONAL

UM NÚMERO CUJA REPRESENTAÇÃO DECIMAL NÃO É PERIÓDICA É CHAMADO NÚMERO. . . E SEU CONJUNTO É REPRESENTADO PELA LETRA I. PREFÍXO I = NÃO É. . . , exemplos: impossível, inimigo, . . .

SÃO NÚMEROS DECIMAIS QUE NÃO ADMITEM A REPRESENTAÇÃO FRACIONÁRIA. SÃO OS DECIMAIS INFINITOS E NÃOPERIÓDICOS VEJA EXEMPLOS:

EXISTEM NÚMEROS IRRACIONAIS NEGATIVOS: LEMBRANDO QUE NÃO EXISTEM RAÍZ QUADRADA DE UM NÚMERO NEGATIVO:

VEJA COMO LOCALIZAR UM NÚMERO IRRACIONAL NUMA RETA NUMÉRICA: TOMA-SE UMA RETA NUMÉRICA E UM QUADRADO DE LADO 1 UNIDADE TRAÇA-SE SUA DIAGONAL. A DIAGONAL DESSE QUADRADO É IGUAL A PARA MARCAR NA RETA A RAIZ QUADRADA DE 2, TRANSPORTE A MEDIDA DA DIAGONAL COM AUXÍLIO DE UM COMPASSO, FIXANDO O VÉRTICE QUE COINCIDE COM A ORIGEM DA RETA NUMERADA, GIRANDO -O NO SENTIDO HORÁRIO ATÉ QUE O GRAFITE INTERCEPTE A RETA.

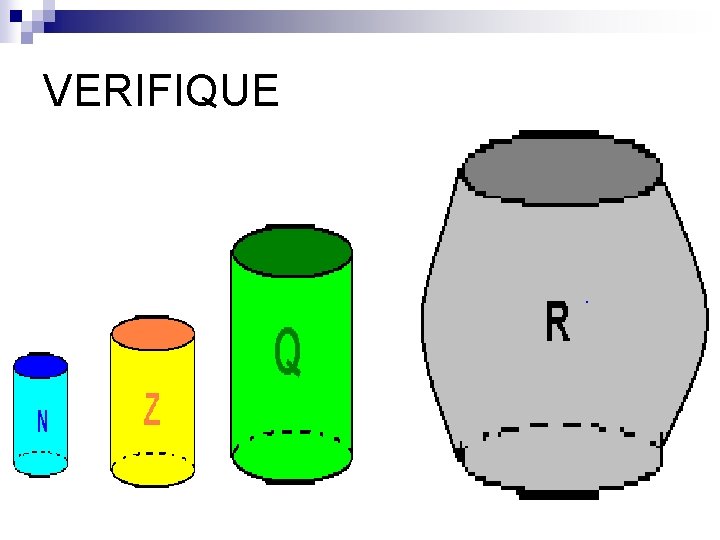
DA REUNIÃO DOS NÚMEROS RACIONAIS E IRRACIONAIS SURGEM OS NÚMEROS REAIS

VERIFIQUE

SÃO REAIS OS NÚMEROS NATURAIS n OS NÚMEROS INTEIROS n OS NÚMEROS RACIONAIS n OS NÚMEROS IRRACIONAIS n POR ISSO É IMPOSSÍVEL ESCREVER OS NÚMEROS REAIS. PARA REPRESENTÁ-LOS USAMOS INTERVALOS, QUE REPRESENTAM SEUS CONJUNTOS Hiperlink para equações

INTERVALOS: INTERVALO É UMA FORMA DE REPRESENTAR SUBCONJUNTOS DOS NÚMEROS REAIS: INTERVALO ABERTO ]a, b[= {x Є R| a < x < b} ou ]a, b[ Bolinhas vazias indicam que os extremos não pertencem ao conjunto

INTERVALO FECHADO [a, b]= {x Є R| a ≤ x ≤ b} [a, b] ou Bolinhas cheias indicam que os extremos pertencem ao conjunto

Um intervalo é chamado misto quando em um extremidade a bolinha é fechada e na outra é aberta, ou vice-versa. . . ]a, b]= {x Є R| a < x ≤ b} [a, b[= {x Є R| a ≤ x < b} EXCLUI-SE O NÚMERO DA BOLINHA ABERTA E INCLUI-SE O DA BOLINHA FECHADA

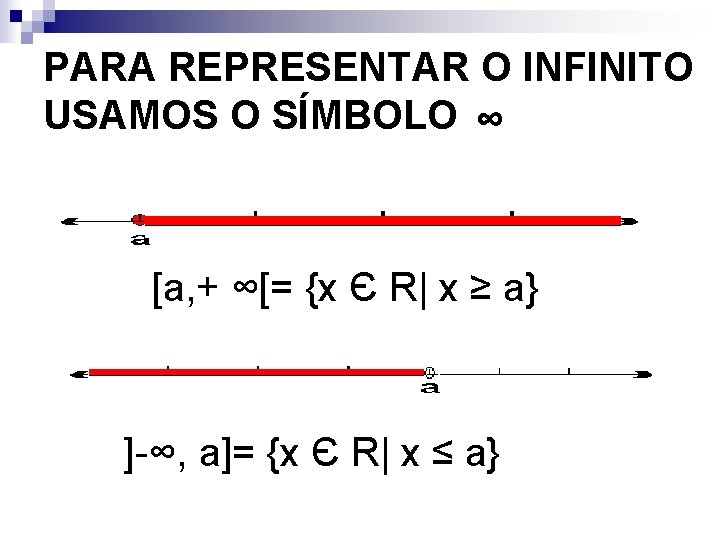
PARA REPRESENTAR O INFINITO USAMOS O SÍMBOLO ∞ [a, + ∞[= {x Є R| x ≥ a} ]-∞, a]= {x Є R| x ≤ a}

jogos

Sites para auxilio no aprendizado: http: //blogmatematic. blogspot. com/2007/10/conjuntos-numricos. html jogos http: //matematicaoitava. blogspot. com/2006/04/conjuntosnumricos. html http: //antigo. revistaescola. abril. com. br/multimidia http: //www. mathema. com. br Procure na página, jogos http: //www. noas. com. br/ensino-fundamental-2/matematica/numeros-nareta/PROJETO

Ficha técnica: CONTEÚDO : CONJUNTOS EIXO: NÚMEROS, OPERAÇÕES E FUNÇÕES HABILIDADES E COMPETÊNCIAS: v. IDENTIFICAR OS DIFERENTES CONJUNTOS NUMÉRICOS E SEUS ELEMENTOS v. SABER RECONHECER SIMBOLOS DE PERTINENCIA E INCLUSÃO NOS CONJUNTOS NUMÉRICOS v. PERCEBER AS PROPRIEDADES DE CADA CONJUNTO NUMÉRICO BEM COMO DE SEUS ELEMENTOS ELABORADO POR CLECIO GERALDO ZANETTI Clecio_zanetti@yahoo. com