Lgica e teoria dos conjuntos Condies e conjuntos

Lógica e teoria dos conjuntos Condições e conjuntos Teste 2

Sempre que tiver dúvidas, consulte o Essencial e recorra ao site http: //www. wolframalpha. com/ para testar as suas hipóteses.

Questão 1 Considere as seguintes condições: a(x): x é um número racional b(x): x é múltiplo de 3 c(x): x é inferior a 25 d(x): x 2 é múltiplo de 4 Indique o valor lógico das proposições: 1. 1 1. 2 1. 3 1. 4 Ver resposta.

Resolução 1. 1 Como π é um número irracional, a(π) é uma proposição falsa. 1. 2 8124 é múltiplo de 3, uma vez que 8 + 1 + 2 + 4 = 15 é múltiplo de 3. Logo, b(8124) é uma proposição verdadeira. Como 122 = 144 = 4 × 36, 122 é múltiplo de 4. Logo, d(12) é uma proposição verdadeira. Como a conjunção de proposições verdadeiras é uma proposição verdadeira, conclui-se que é uma proposição verdadeira.

Resolução 1. 3 Como é um número inferior a 25, é uma proposição verdadeira. Como 3 + 7 + 3 = 13 não é múltiplo de 3, 373 não é múltiplo de 3 e, portanto, b(373) é uma proposição falsa. Sabendo que a equivalência entre duas proposições é verdadeira se, e só se, ambas tiverem o mesmo valor lógico, conclui-se que é uma proposição falsa.

Resolução 1. 4 é verdadeira porque é um número racional. Logo, como a disjunção de proposições é falsa se, e só se, ambas forem falsas, é verdadeira. é falsa, uma vez que 25 não é inferior a 25. Logo, é verdadeira. Portanto, é verdadeira.

Questão 2 Para cada uma das condições seguintes indique se é universal, possível ou impossível nos universos indicados: 2. 1 2. 2 2. 3 2. 4 Ver respostas. em IR

Resolução 2. 1 . Logo, é uma condição possível em IR. 2. 2 . Logo, em IN, pois tem soluções naturais: é uma condição possível. 2. 3 Logo, é uma condição impossível em IR. 2. 4 Logo, é uma condição universal em IR.

Questão 3 Utilizando quantificadores, traduza, em linguagem simbólica, cada uma das expressões, indicando o seu valor lógico: 3. 1 Qualquer número inteiro é real. 3. 2 Existe pelo menos um número racional cujo quadrado é igual ao seu dobro. 3. 3 Existe pelo menos um número inteiro que não é positivo nem negativo. 3. 4 Nenhum número real é solução da equação x 2 + 1 = 0. Ver respostas.

Resolução 3. 1 ou . 3. 2 3. 3 3. 4 ou São todas verdadeiras. .

Questão 4 Considere os seguintes conjuntos: Verifique se: Ver resposta. .

Resolução 4. Consideremos os seguintes conjuntos: Verificar se é equivalente a verificar se A = B. Observe-se que: Logo, como A = B, conclui-se que .

Questão 5 Escreva, em linguagem simbólica, a negação das seguintes proposições sem usar o símbolo ~, e indique o seu valor lógico: 5. 1 5. 2 5. 3 Ver respostas.

Resolução 5. 1 A negação de é dada por O seu valor lógico é falso (por exemplo, 3 + 3 < 5 é falso). 5. 2 A negação de é dada por. O seu valor lógico é falso. 5. 3 A negação de é dada por. O seu valor lógico é falso (por exemplo, é falso).

Questão 6 Considere os seguintes conjuntos: Defina em extensão os conjuntos: 6. 1 A. Ver respostas. 6. 2 B. 6. 3 C. 6. 4 CA. 6. 5 A B C. Ver respostas.

Resolução 6. 1 6. 2 6. 3

Resolução 6. 4 6. 5

Questão 7 Indique se, para qualquer concretização das variáveis no conjunto U, se obtêm, das seguintes condições, implicações verdadeiras, e escreva as respetivas contrarrecíprocas. 7. 1 7. 2 x é múltiplo de 8 Ver respostas. x é par 7. 3 Se um quadrilátero tem diagonais perpendiculares, então, é um quadrado (U é o conjunto dos quadriláteros do plano). 7. 4 Ver respostas.

Resolução 7. 1 A implicação é verdadeira para qualquer concretização da variável em IR, porque . O contrarrecíproco é dado por. 7. 2 x é múltiplo de 8 x é par . A implicação é verdadeira para qualquer concretização da variável em IN porque se x for múltiplo de 8, então, x = 8 k, para algum número natural k. Logo, x é par porque x = 2(4 k). O contrarrecíproco é dado por: x é ímpar x não é múltiplo de 8.

7. 3 Se um quadrilátero tem diagonais perpendiculares, então, é um quadrado (U é o conjunto dos quadriláteros do plano). A implicação é falsa porque, por exemplo, um losango é um quadrilátero do plano com diagonais perpendiculares e não é um quadrado. O contrarrecíproco é: se um quadrilátero não é um quadrado, então, não tem diagonais perpendiculares. 7. 4 A implicação não é verdadeira para a concretização da variável O contrarrecíproco é: . .

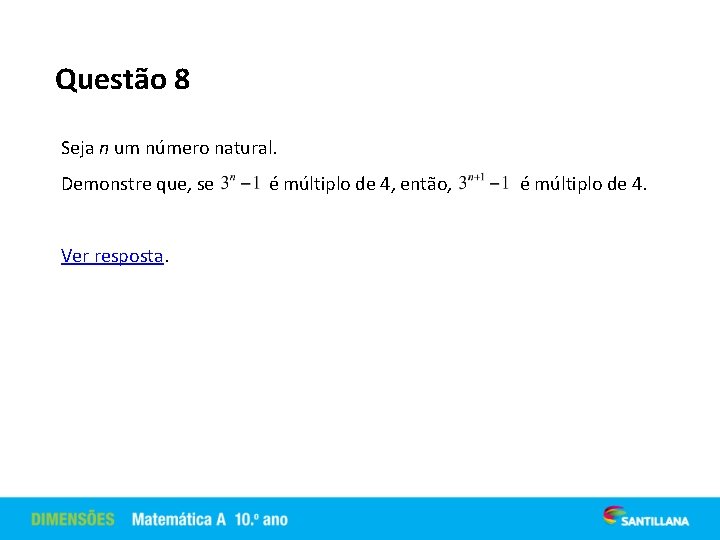
Questão 8 Seja n um número natural. Demonstre que, se Ver resposta. é múltiplo de 4, então, é múltiplo de 4.

Resolução 8. Seja n um número natural, tal que 3 n é múltiplo de 4. Então, existe um número natural k, tal que 3 n = 4 k. Então, 3 n + 1 = 3 n × 3 = 4 k × 3 = 4 × (3 k). Então, considerando k’ = 3 k, existe um número natural k’, tal que 3 n + 1 = 4 × k’, ou seja, 3 n + 1 é múltiplo de 4. c. q. d.

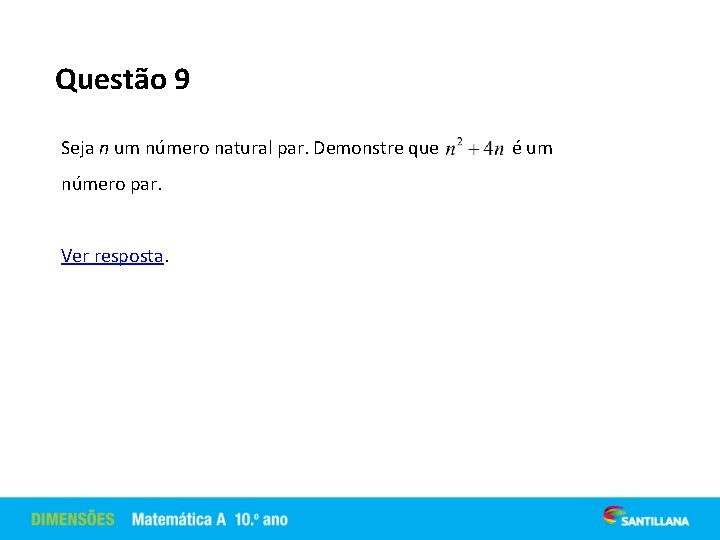
Questão 9 Seja n um número natural par. Demonstre que número par. Ver resposta. é um

Resolução 9. Seja n um número natural. Se n for par, então, n + 4 é par. Como o produto de dois números é ímpar se, e só se, os dois forem ímpares, conclui-se que é par.

Questão 10 Demonstre, por contrarrecíproco, que se um número natural n não é divisível por 5, então, não é divisível por 20. Ver resposta.

Resolução 10. Demonstrar que; se um número natural n não é divisível por 5, então, não é divisível por 20 por contrarrecíproco; é demonstrar que se um número natural n é divisível por 20, então, é divisível por 5. Consideremos, assim, um número natural n divisível por 20. Então, existe um número natural k, tal que n = 20 k, ou seja, n = 5(4 k). Então, existe um número natural k’ = 4 k, tal que n = 5 k’, ou seja, n é divisível por 5. Assim, demonstrou-se, por contrarrecíproco, que se um número natural n não é divisível por 5, então, não é divisível por 20. c. q. d.