Teoria dos Conjuntos Prof Jorge Conjuntos Conceitos iniciais

Teoria dos Conjuntos Prof. Jorge

Conjuntos – Conceitos iniciais q Na teoria dos conjuntos, consideramos como primitivos os conceitos de elemento, pertinência e conjunto. Exemplos - Conjunto I. O conjunto dos alunos do 1º ano do Colégio Nóbrega. II. O conjunto de todos os números inteiros. III. O conjunto de todos os números reais que é solução da equação x 2 – 16 = 0. Ø Em geral, utilizamos letras latinas maiúsculas para representar conjuntos. A, B, C, . . . , Z. Prof. Jorge

Conjuntos – Conceitos iniciais q Na teoria dos conjuntos, consideramos como primitivos os conceitos de elemento, pertinência e conjunto. Exemplos – Elemento I. Pedro é um elemento do conjunto dos alunos do 1º ano do Colégio Nóbrega. II. 7 é um elemento do conjunto dos números inteiros. III. +4 é um elemento do conjunto dos números reais que satisfaz à equação x 2 – 16 = 0. Ø Em geral, utilizamos letras latinas minúsculas para representar elementos. a, b, c, . . . , z. Prof. Jorge

Conjuntos – Conceitos iniciais q Na teoria dos conjuntos, consideramos como primitivos os conceitos de elemento, pertinência e conjunto. Exemplos – Pertinência I. Pedro pertence ao conjunto dos alunos do 1º ano do Colégio Nóbrega. II. 7 pertence ao conjunto dos números inteiros. III. +4 pertence ao conjunto dos números reais que satisfaz à equação x 2 – 16 = 0. Ø Utilizamos o símbolo “pertence” e “não pertence” para relacionar elemento e conjunto. Prof. Jorge

Notações de Conjuntos q Um conjunto pode ser representado: Ø Enumerando seus elementos entre chaves, separados por vírgulas; Ø Indicando, entre chaves, uma propriedade que caracterize cada um de seus elementos; Ø Por meio de uma figura fechada, dentro da qual podem-se escrever seus elementos. “Diagrama de Venn-Euler”. Prof. Jorge

Exemplo n Representar o conjunto V das vogais. ü V = {a, e, i, o, u} ü V = {x; x é vogal} V ü como no diagrama ao lado a i u ü No caso a V, mas m V. Prof. Jorge o e

Observação q Há conjuntos com apenas: Ø Um único elemento, chamados conjuntos unitários; Ø Nenhum elemento, chamados conjunto vazio; Ø Infinitos elementos, chamados conjuntos infinitos. ü O conjunto vazio pode ser representado pelos símbolos { } e Ø. Prof. Jorge

Exemplos n A = {x; x é inteiro positivo, par e primo} A = {2} n B = {x; x é inteiro, ímpar e divisível por 2} B={}=Ø n C = {a; a é número natural ímpar e primo} C = {3, 5, 7, 11, 13, 17, 19, . . . } Prof. Jorge

Observação q Se dois conjuntos possuem exatamente os mesmos elementos (não importando a ordem em que eles aparecem), dizemos que eles são conjuntos iguais. Ø A = {x; x é inteiro positivo e x < 4} Ø B = {2, 3, 1} A = {1, 2, 3} = B. Se x A ⇒ x B Se x B ⇒ x A A=B ⇔ Prof. Jorge

Exemplo n A = Conjunto das letras da palavra TRATOR n B = Conjunto das letras da palavra ATOR A = {t, r, a, o} B = {a, t, o, r} A=B Prof. Jorge

Subconjuntos q Se todo elemento de um conjunto A é também elemento de um conjunto B, dizemos que: ü A está contido em B (símbolo: A ⊂ B); ü B contém A (símbolo: B ⊃ A); ü A é subconjunto de B; ü A é parte de B. Prof. Jorge B A

Exemplo n A = {x ℕ; x < 4} n B = {x ℝ; x(x – 1) = 0} A = {0, 1, 2, 3} e B = {0, 1} Podemos afirmar que B é um subconjunto de A (B ⊂ A). A B 0 2 3 Prof. Jorge 1

Observação – subconjuntos q q q Se um conjunto A é igual a um conjunto B (A = B), então A ⊂ B e B ⊂ A. Se A ≠ B, A ≠ Ø e A ⊂ B, dizemos que A é subconjunto próprio de B. O conjunto vazio está contido em qualquer conjunto (Ø ⊂ A, para todo A) Ø O vazio é subconjunto de qualquer conjunto; Ø Todo conjunto é subconjunto de si mesmo. Prof. Jorge

Exemplo n Encontrar todos os subconjuntos de A = {1, 2, 3}. ü Com 0 elemento → Ø ü Com 1 elemento → {1}, {2}, {3} ü Com 2 elementos → {1, 2}, {1, 3}, {2, 3} ü Com 3 elementos → {1, 2, 3} Ø Dizemos que Ø e A = {1, 2, 3} são subconjuntos triviais de A. Os outros são os subconjuntos próprios de A. Prof. Jorge

Observação – subconjuntos q Chamamos de conjunto das partes do conjunto A e representamos por P(A), o conjunto de todos os subconjuntos do conjunto A. Exemplo Ø A = {1, 2, 3} Ø Subconjuntos de A: Ø, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} P(A) = {Ø, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} n(P(A)) = 2 n(A) Prof. Jorge

Exemplo n Se um conjunto A tem n elementos e 128 subconjuntos, quantos elementos possui o conjunto A? 2 n = 128 ⇒ 2 n = 2 7 ⇒ Logo, o conjunto A tem 7 elementos. Prof. Jorge n=7

Operações com Conjuntos Prof. Jorge

Operações com Conjuntos q A partir de dois conjuntos conhecidos, A e B, podemos obter outros conjuntos, operando com os conjuntos dados. Definimos as operações a seguir: I. União; II. Interseção; III. Diferença; Prof. Jorge

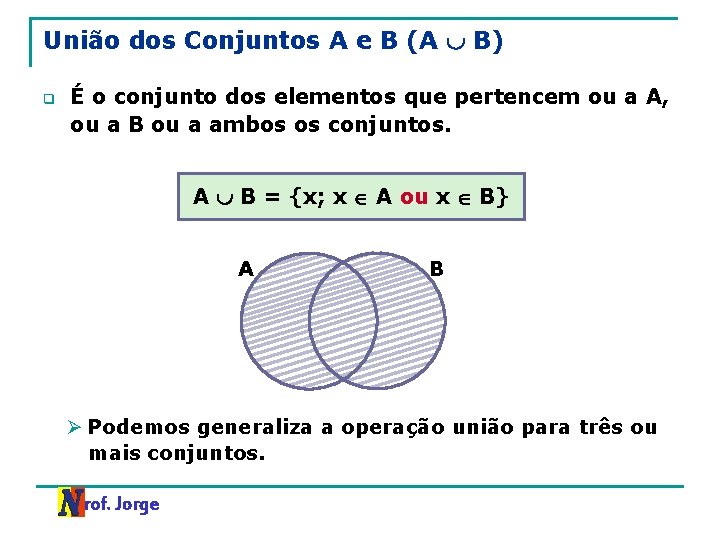
União dos Conjuntos A e B (A B) q É o conjunto dos elementos que pertencem ou a A, ou a B ou a ambos os conjuntos. A B = {x; x A ou x B} A B Ø Podemos generaliza a operação união para três ou mais conjuntos. Prof. Jorge

Exemplo n Dados os conjuntos A = {0, 1, 2, 3, 4}, B = {1, 3, 5, 7} e C = {5, 6, 7, 8, 9}, vamos obter: a) A B. b) A B C. ü a) A B = {0, 1, 2, 3, 4, 5, 7} ü b) A B C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Ø No caso de três ou mais conjuntos, podemos escrever A B C = (A B) C = A (B C). Prof. Jorge

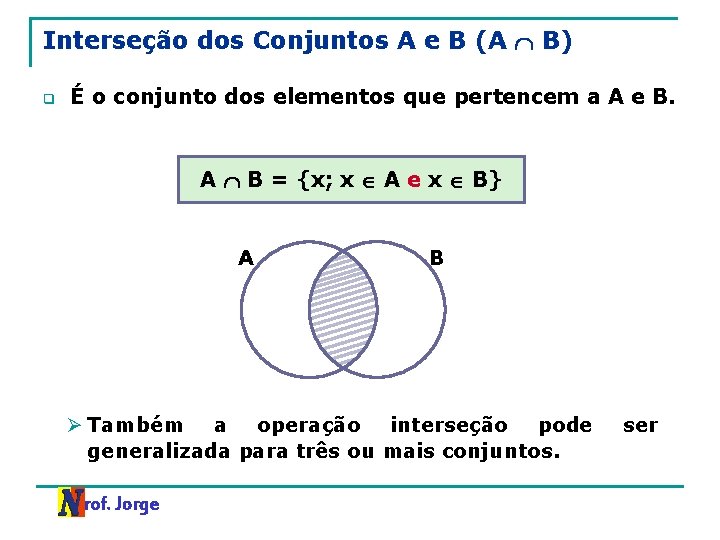
Interseção dos Conjuntos A e B (A B) q É o conjunto dos elementos que pertencem a A e B. A B = {x; x A e x B} A B Ø Também a operação interseção pode generalizada para três ou mais conjuntos. Prof. Jorge ser

Exemplo n Dados os conjuntos A = {0, 1, 5}, B = {0, 2, 5, 7}, C = {4, 6, 7, 9} e D = {0, 1, 6}, vamos obter: a) A B. b) A C. c) A B D. ü a) A B = {0, 5} ü b) A C = Ø ü c) A B D = {0} Prof. Jorge Logo, A e C são disjuntos

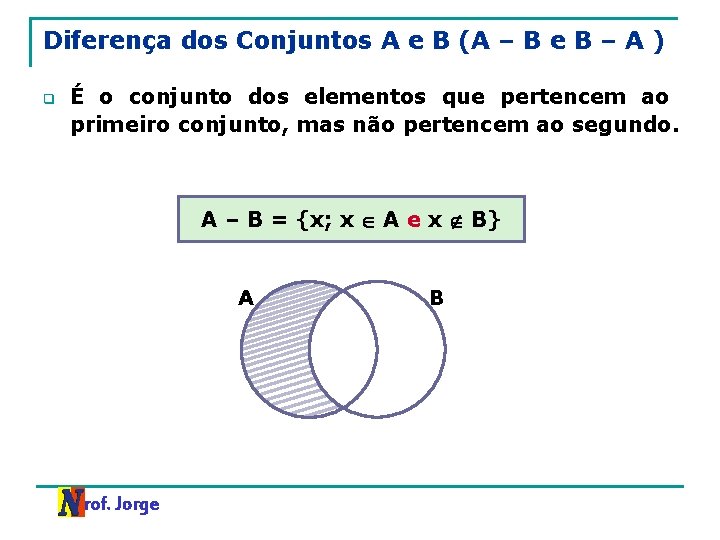
Diferença dos Conjuntos A e B (A – B e B – A ) q É o conjunto dos elementos que pertencem ao primeiro conjunto, mas não pertencem ao segundo. A – B = {x; x A e x B} A Prof. Jorge B

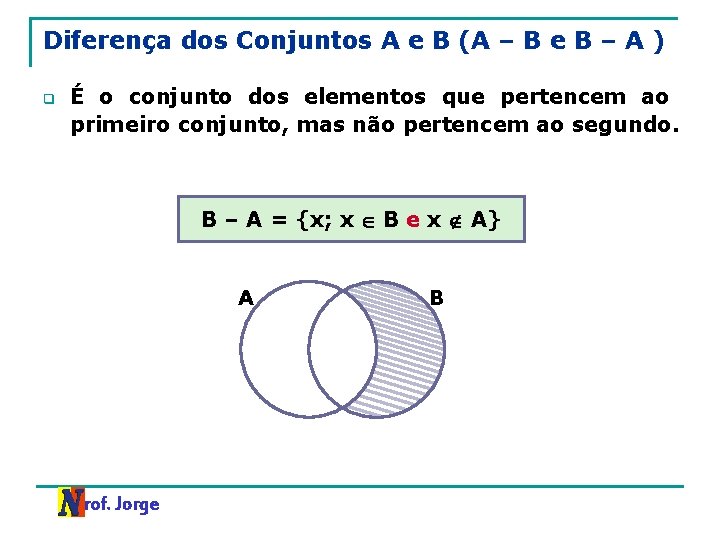
Diferença dos Conjuntos A e B (A – B e B – A ) q É o conjunto dos elementos que pertencem ao primeiro conjunto, mas não pertencem ao segundo. B – A = {x; x B e x A} A Prof. Jorge B

Exemplos n Dados os conjuntos A = {1, 2, 3, 4, 5}, B = {2, 4, 6}, vamos obter: a) A – B. b) B – A. ü a) A – B = {1, 2, 3, 4, 5} – {2, 4, 6} = {1, 3, 5} ü b) B – A = {2, 4, 6} – {1, 2, 3, 4, 5} = {6} Ø Em geral A – B ≠ B – A. Prof. Jorge

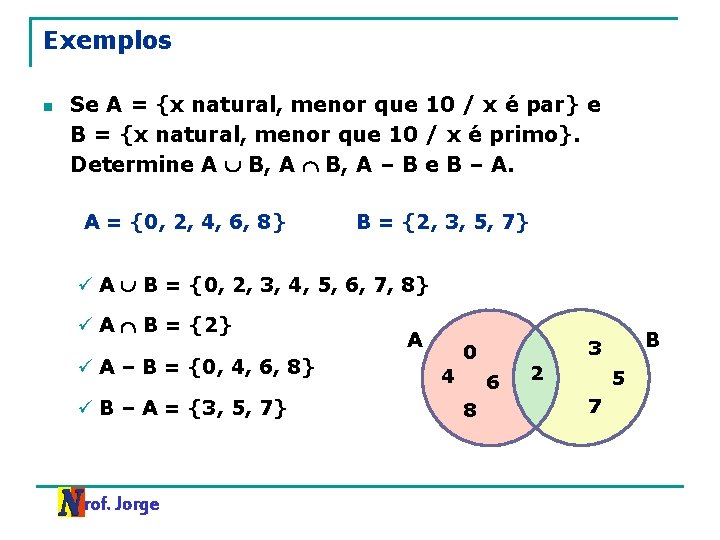
Exemplos n Se A = {x natural, menor que 10 / x é par} e B = {x natural, menor que 10 / x é primo}. Determine A B, A – B e B – A. A = {0, 2, 4, 6, 8} B = {2, 3, 5, 7} ü A B = {0, 2, 3, 4, 5, 6, 7, 8} ü A B = {2} ü A – B = {0, 4, 6, 8} ü B – A = {3, 5, 7} Prof. Jorge A 4 6 8 B 3 0 2 5 7

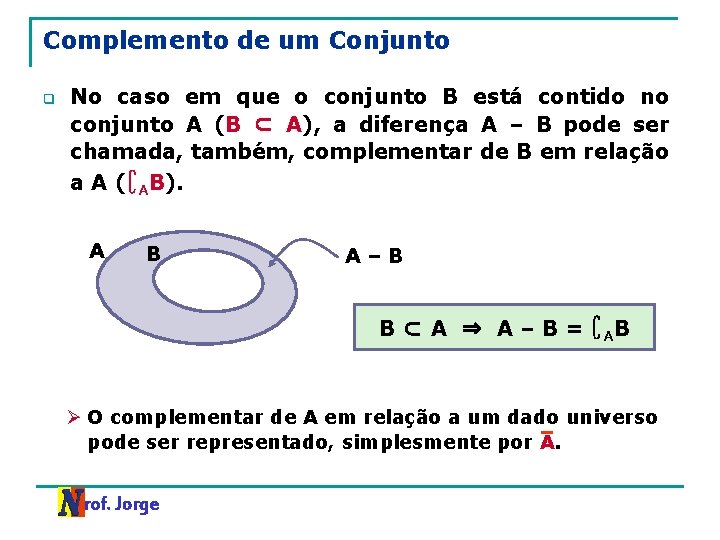
Complemento de um Conjunto q No caso em que o conjunto B está contido no conjunto A (B ⊂ A), a diferença A – B pode ser chamada, também, complementar de B em relação a A (∁AB). A B A–B B ⊂ A ⇒ A – B = ∁AB Ø O complementar de A em relação a um dado universo pode ser representado, simplesmente por A. Prof. Jorge

Exemplos n Dados os conjuntos X = {1, 2, 4}, Y = {1, 2, 3, 4, 5}, X ⊂ Y. Obter ∁YX = Y – X = {1, 2, 3, 4, 5} – {1, 2, 4} = {3, 5} n Se A = {x ℝ; x > 2}, A está contido no universo ℝ. Obter ∁A. ∁A = {x ℝ; x ≤ 2} Prof. Jorge

Exemplos n Se A = {a, b, c, d, e} e B = {d, e, f, g} estão contidos no universo U = {a, b, c, d, e, f, g, h}, determinar o conjunto ∁A B. ∁A = U – A = {f, g, h} ∁A B = {f, g, h} {d, e, f, g} = {f, g} Prof. Jorge

Número de elementos da união de conjuntos Prof. Jorge

Número de elementos da união de conjuntos q Existe uma relação importante que envolve a quantidade de elementos dos seguintes conjuntos finitos: A, B, A B e A B. Observe: n(A B) = n(A) + n(B) – n(A B) ü n(A) = número de elementos do conjunto A ü n(B) = número de elementos do conjunto B ü n(A B) = número de elementos da interseção ü n(A B) = número de elementos da união Prof. Jorge

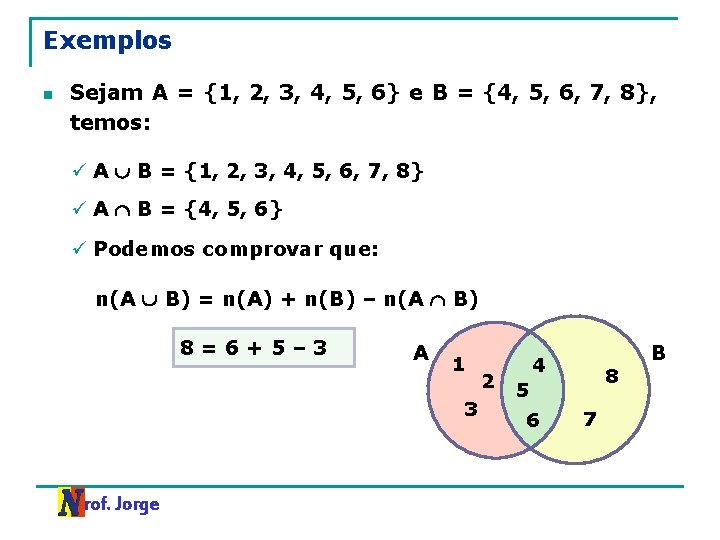
Exemplos n Sejam A = {1, 2, 3, 4, 5, 6} e B = {4, 5, 6, 7, 8}, temos: ü A B = {1, 2, 3, 4, 5, 6, 7, 8} ü A B = {4, 5, 6} ü Podemos comprovar que: n(A B) = n(A) + n(B) – n(A B) 8=6+5– 3 A 1 3 Prof. Jorge 2 B 4 8 5 6 7

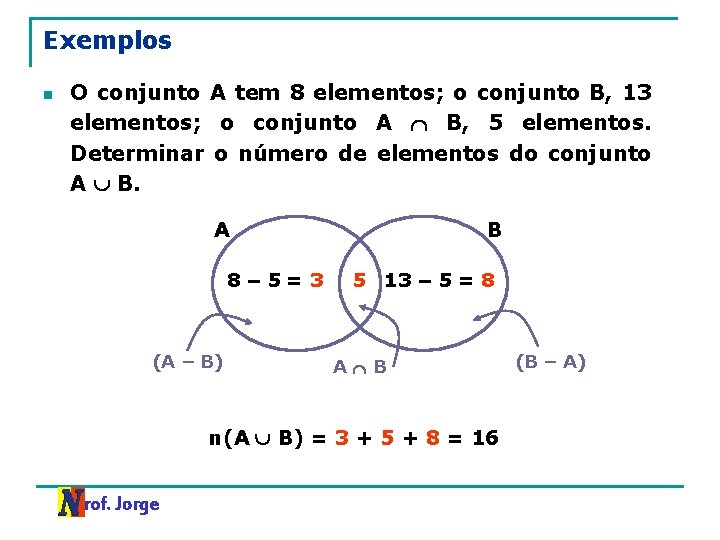
Exemplos n O conjunto A tem 8 elementos; o conjunto B, 13 elementos; o conjunto A B, 5 elementos. Determinar o número de elementos do conjunto A B. A 8– 5=3 (A – B) B 5 13 – 5 = 8 A B n(A B) = 3 + 5 + 8 = 16 Prof. Jorge (B – A)

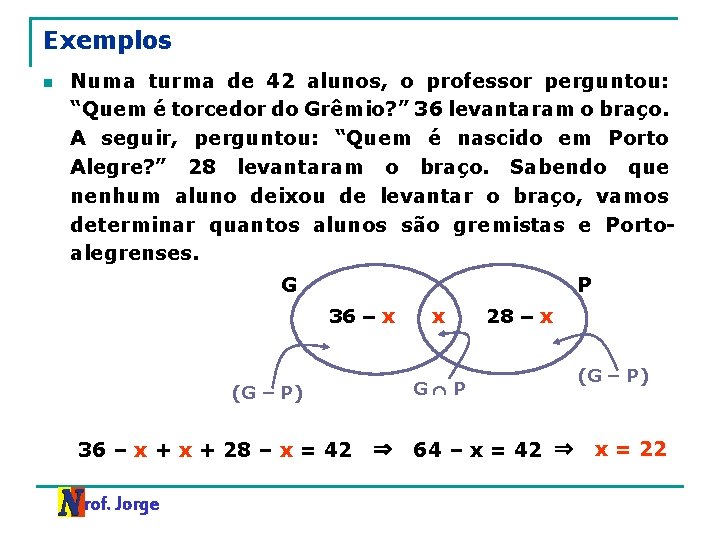
Exemplos n Numa turma de 42 alunos, o professor perguntou: “Quem é torcedor do Grêmio? ” 36 levantaram o braço. A seguir, perguntou: “Quem é nascido em Porto Alegre? ” 28 levantaram o braço. Sabendo que nenhum aluno deixou de levantar o braço, vamos determinar quantos alunos são gremistas e Portoalegrenses. G P 36 – x Prof. Jorge 28 – x G P (G – P) 36 – x + 28 – x = 42 x ⇒ 64 – x = 42 ⇒ (G – P) x = 22