Teoria dos conjuntos Conjunto coleo classe grupo ou

Teoria dos conjuntos Conjunto – coleção, classe , grupo ou lista de elementos Designados por letras maiúsculas e um conjunto vazio é designado por Um conjunto fica definido se forem indicados todos os seus elementos, uns após os outros, separados por vírgula e entre chaves.

Se a é um elemento de S, isto é, se a pertence a S, tem-se: Se b não é um elemento de S, isto é, se b não pertence a S tem-se: Exemplos

Relações entre conjuntos Conjuntos iguais – se ambos contém exatamente os mesmos elementos A=B Exemplos Tem-se A = C, A D e. C D

Subconjunto Se todo elemento de A é também elemento de S, A é um subconjunto de S e pode-se escrever A S • Todo conjunto é subconjunto de si próprio • Todo conjunto tem como subconjunto o conjunto vazio Tem-se

Operações com conjuntos União A união de dois conjuntos A e B é um conjunto cujos elementos são os elementos que pertencem a A, a B ou a ambos. Exemplo

Interseção A interseção de dois conjuntos A e B é um conjunto dos elementos que pertencem tanto ao conjunto A como ao conjunto B, isto é, dos elementos comuns aos dois conjuntos Exemplo

Conjuntos disjuntos Não possuem elementos comuns Exemplo

Complemento Se A é um subconjunto de S, o conjunto dos elementos que pertencem a S e não pertencem a A é denominado complemento de A em relação a S e é indicado por

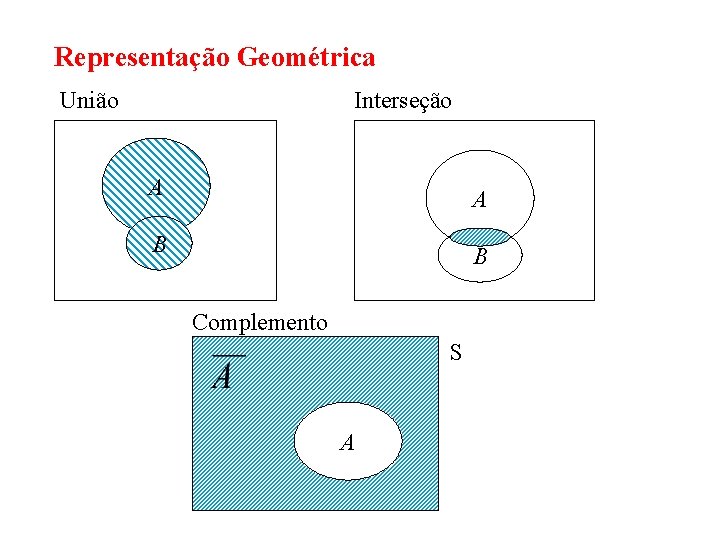
Representação Geométrica União Interseção A A B B Complemento S A

Propriedades A união e a interseção de conjuntos são propriedades comutativas a+b = b+a ab = ba A união e a interseção de conjuntos são propriedades associativas (a+b)+c = a+(b+c) (ab)c = a(bc)

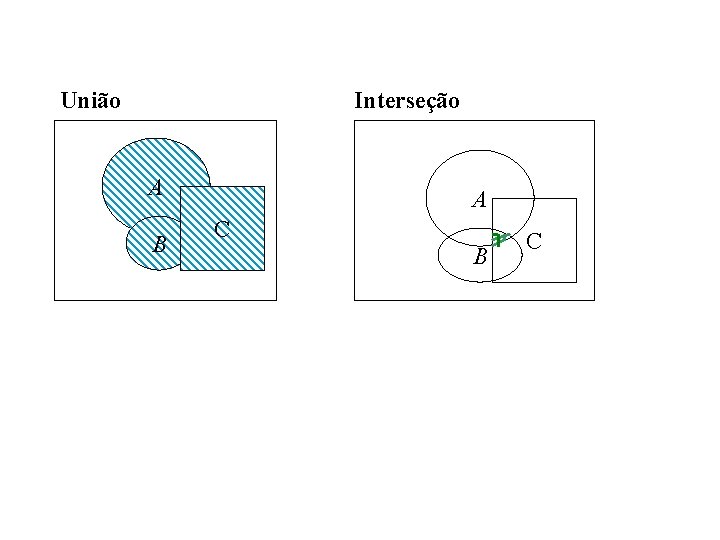
União Interseção A B A C B C

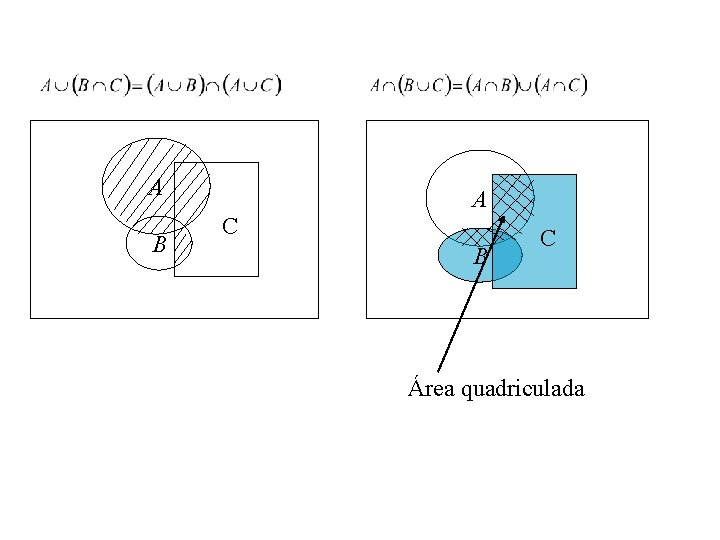
Combinação de operações de união e interseção Propriedade distributiva a(b+c) = ab+ac Propriedade distributiva da multiplicação em relação à soma

A B A C B C Área quadriculada

Probabilidade Experimento: Todo fenômeno ou ação que geralmente pode ser repetido e cujo resultado é casual ou aleatório. Ex: jogar um dado Espaço amostral: conjunto de todos os resultados possíveis de um experimento. Evento: todo subconjunto do espaço amostral. Evento simples ou elementar: todo subconjunto unitário do espaço amostral.

O espaço amostral relativo a um experimento pode ser representado de várias formas: 1) Lançamento de um dado E = {1, 2, 3, 4, 5, 6} 2) Lançamento de duas moedas E = {KK, KC, CK, CC} 3) Número de caras obtidas no lançamento de duas moedas E = {0, 1, 2} 4) Lançamento de uma moeda uma única vez E = {K, C}

Probabilidade 1 - Definição clássica: se um espaço amostral é constituído por n eventos mutuamente exclusivos e igualmente prováveis e se n. A desses eventos têm o atributo A, então a probabilidade de A é: P(A) = n. A/n Ex: Lançamento de um dado – a probabilidade associada a cada um dos eventos é 1/6. Crítica: ao se exigir que os n eventos possíveis sejam igualmente prováveis, utiliza-se o conceito que se pretende definir.

2 - Probabilidade como limite de freqüência relativa Freqüência relativa do evento A é o quociente entre o número de vezes que o evento ocorreu (n. A) e o número total de eventos observados (n).

Ex. : Sejam K e C os eventos cara e coroa relativos ao lançamento de uma moeda uma única vez. Se a moeda é feita de material homogêneo tem-se P(K) = P(C) = 0, 5. Entretanto, se a moeda não for feita de material homogêneo para obter P(K) é necessário lançar uma moeda um número suficientemente grande de vezes e calcular: onde n. K é o número de vezes que saiu cara em n lançamentos da moeda.

Criticas: 1. Se limita a casos em que o número de eventos observados pode crescer indefinidamente. 2. Não é possível uma interpretação rigorosa sem usar o próprio conceito de probabilidade. É um conceito útil na prática – companhias de seguros usam o conceito.

3 - O conceito moderno de probabilidade Seja E um espaço amostral e seja A qualquer evento de E, isto é, A é um subconjunto de E. Então, por definição, a probabilidade de ocorrer A é dada pela medida de A, nas seguintes condições: 1) A medida do universo é 1: P(E) = 1 2) A medida é não negativa: P(A) > 0 3) Se A e B são dois eventos disjuntos, P(A B) = P(A) + P(B) Desses postulados segue-se que: 0 P(A) 1

O caso mais simples para se determinar a probabilidade é aquele em que o universo é constituído por n eventos elementares e, por razão de simetria, os eventos são igualmente prováveis; nesse caso, a probabilidade de cada evento elementar é 1/n. Assim, a probabilidade de sair 5 em um lançamento de um dado não chumbado é 1/6.

A probabilidade do complemento e o teorema da soma Teorema: Seja E o espaço amostral. Então, a probabilidade de que A não ocorra é: Teorema da soma: Se A e B são dois eventos do espaço amostral E, então a probabilidade de que ocorra A ou B é: Se A e B são disjuntos

Exemplos: lançamento de um dado A: sair resultado par, isto é, A = {2, 4, 6} B: sair resultado inferior a 3, isto é, B = {1, 2} A é a união de três elementos, cada um com probabilidade 1/6. B é a união de dois elementos, cada um com probabilidade 1/6 Probabilidade de ocorrer A ou B? Tem-se, de acordo com o teorema da soma que: P(A) = 3/6 = 1/2 P(B) = 2/6 = 1/3 P( A ) = 1 - 1/2 ={1, 2, 4, 6} O problema também poderia ser resolvido assim:

Probabilidade condicional e o teorema do produto A: sair resultado par, isto é, A={2, 4, 6} B: sair resultado inferior a 3, isto é, B={1, 2} Segue-se que Foi visto que

Considere a seguinte situação: Um dado foi lançado fora do alcance de nossas vistas e fomos informados que saiu valor par, ou seja, que ocorreu A. Nessas condições, qual é probabilidade de que tenha ocorrido o evento B? A: sair resultado par, isto é, A ={2, 4, 6} B: sair resultado inferior a 3, isto é, B ={1, 2}

Probabilidade condicional A ={2, 4, 6} B ={1, 2} Se fomos informados que ocorreu A, o espaço amostral passou a ser A. Então: Se dividirmos o numerador e o denominador por 6, que é o número total de eventos do universo original tem-se: Teorema do produto Se A e B são dois eventos do espaço amostral E, a probabilidade da ocorrência simultânea de A e B é dada por:

Considere agora a seguinte situação: Um dado foi lançado fora do alcance de nossas vistas e fomos informados que saiu valor inferior a 3, ou seja, que ocorreu B. Nessas condições, qual é probabilidade de que tenha ocorrido o evento A? A: sair resultado par, isto é, A ={2, 4, 6} B: sair resultado inferior a 3, isto é, B ={1, 2}

Probabilidade condicional Se fomos informados que ocorreu B, o espaço amostral passou a ser B. Então: Se dividirmos o numerador e o denominador por 6, que é o número total de eventos do universo original tem-se: Teorema do produto Se A e B são dois eventos do espaço amostral E, a probabilidade da ocorrência simultânea de A e B é dada por:

Eventos Independentes Um evento A é estatisticamente independente do evento B se O fato de A ser independente de B implica em B ser independente de A O teorema do produto para eventos independentes

Combinações e permutações Dado m diferentes elementos, o número de combinações de n elementos que se pode fazer é: Dado m diferentes elementos, o número de permutações que se pode fazer é igual a m!

Teorema de BAYES Dado um experimento em dois estágios e conhecidas as probabilidades a priori e as probabilidades condicionais, o teorema de BAYES permite calcular as probabilidades a posteriori, isto é, as probabilidades associadas aos resultados do primeiro estágio dado o resultado do segundo estágio. Exemplo Plantas doentes (e 1) Plantas não doentes (e 2) Folhas murchas (f 1) Folhas não murchas (f 2) Probabilidade das plantas adoecerem Probabilidade das plantas não adoecerem P(e 1) = 0, 5 P(e 2) = 0, 5

Probabilidades a priori Probabilidade das folhas murcharem dado que a planta está doente P(f 1/e 1) = 0, 80 Probabilidade das folhas não murcharem dado que a planta está doente P(f 2/e 1) = 0, 20 Probabilidade das folhas murcharem dado que a planta não está doente P(f 1/e 2) = 0, 30 Probabilidade das folhas não murcharem dado que a planta não está doente P(f 2/e 2) = 0, 70

Cálculo das probabilidades a posteriori Probabilidade da planta estar doente dado que a folha está murcha P(e 1/f 1) = ? Probabilidade da planta estar doente dado que a folha não está murcha P(e 1/ f 2) = ? Probabilidade da planta não estar doente dado que a folha está murcha P(e 2/ f 1) = ? Probabilidade da não planta não estar doente dado que a folha não está murcha P(e 2/f 2) = ?

Lembrando Generalizando

Probabilidade da planta estar doente dado que as folhas estão murchas

Exercícios 1. Sendo defeituosos 10% dos rádios produzidos por uma indústria, se forem examinados, ao acaso, três rádios por ela produzidos, qual é a probabilidade de nenhum ter defeito? 2. Uma urna contém quatro bolas brancas e duas pretas. Outra urna contém três bolas brancas e cinco pretas. Se for retirada uma bola de cada urna, qual é a probabilide de: a) uma das bolas ser branca e a outra ser preta b) ambas as bolas serem pretas c) ambas as bolas serem brancas

1) 9/10 x 9/10 = 0, 729 2) a) 4/6 x 5/8 + 2/6 x 3/8 = 13/24 b) 2/6 x 5/8 = 5/24 c) 4/6 x 3/8 = 1/4

3. Uma urna contém 5 bolas pretas, 3 brancas e 2 vermelhas. Três bolas são retiradas da urna, uma após a outra. Determine a probabilidade de as bolas retiradas serem da mesma cor, admitindo-se que: - as bolas foram repostas após cada retirada - não houve reposição 4. Jogando-se um dado duas vezes, qual é a probabilidade de a soma dos pontos ser igual a 3? 5. Sabe-se que um casal tem dois filhos. Sabe-se que um deles é do Sexo masculino. Qual é a probabilidade de o outro filho ser do sexo feminino?

3. a) 5/10 x 5/10 + 3/10 x 3/10 + 2/10 x 2/10 = 0, 16 b) 5/10 x 4/9 x 3/8 + 3/10 x 2/9 x 1/8 = 11/120 4. 2/36 5. 2/3 masc fem masc

6. Dois dados são lançados simultaneamente. Defini-se os eventos: A: sair valor par em ambos B: sair valor ímpar em ambos C: sair soma igual a seis A e B são mutuamente exclusivos? A e C são mutuamente exclusivos? C e B são mutuamente exclusivos? A e B são independentes? A e C são independentes? B e C são independentes? Quanto valem P(A/C), P(C/A), P(A/B), P(B/C) e P(C/B)

P(A) = 3/6 x 3/6 = 9/36 = ¼ P(B) = 3/6 x 3/6 = 9/36 = ¼ P (C) = 5/36 P(A/C) = 2/5 P(C/A) = 2/9 P(A/B) = 0 P(B/C) = 3/5 P(A/C) = 3/9 São mutuamente exclusivos Não

São independentes? P(A/B) = 0, diferente de P(A) = 1/4 P(A/C) = 2/5, diferente de P(A) = 1/4 P(B/C) = 3/5, diferente de P(B) = 1/4 Portanto, não são independentes.

Resolver: Em uma fábrica quatro máquinas produzem o mesmo produto. A máquina A produz 10% do total produzido. A máquina B produz 20%, a C produz 30% e a D produz 40%. A proporção de produtos defeituosos de cada máquina é a seguinte: máquina A = 0, 001; máquina B = 0, 0005; máquina C = 0, 005 e máquina D = 0, 002. Um item é selecionado ao acaso e verifica-se que ele tem defeito. Qual é a probabilidade de que esse item tenha sido produzido pela máquina A.