CONJUNTOS NUMRICOS e TEORIA DOS NMEROS NMEROS NATURAIS




























- Slides: 31

CONJUNTOS NUMÉRICOS e TEORIA DOS NÚMEROS

NÚMEROS NATURAIS 1 “São os números que 2 usamos quando precisamos 3 contar coisas. ” 4

São todos os números inteiros nãonegativos. N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, . . . } N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, . . . }

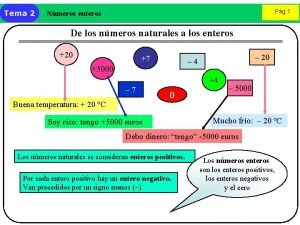
NÚMEROS INTEIROS Como efetuar a subtração de 3 – 4? Pelos Naturais é impossível!

“São todos os números que pertencem aos Naturais acrescido dos seus respectivos opostos. ” Z = {. . . -4, -3, -2, -1, 0, 1, 2, 3, 4, . . . }

SUBCONJUNTOS DOS INTEIROS 1. Inteiros não Negativos (Z+): Z+ = {0, 1, 2, 3, 4, 5, 6, . . . } 2. Inteiros não Positivos (Z-): Z- = {. . . , -6, -5, -4, -3, -2, -1, 0}

SUBCONJUNTOS DOS INTEIROS 3. Inteiros não negativos e não nulos (Z*+): Z*+ = { 1, 2, 3, 4, 5, 6, . . . } 4. Inteiros não positivos e não nulos (Z*-): Z*- = {. . . , -6, -5, -4, -3, -2, -1}

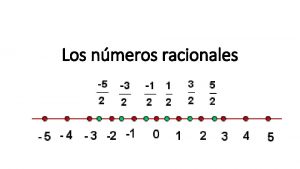
NÚMEROS RACIONAIS Como dividir um osso para dois cachorros? Os Inteiros não permitem a resolver este problema!

“Para resolver isso foram criados os números fracionários. ” Q = Z { números fracionários } Q = {a/b | a, b Z e b 0}

SUBCONJUNTOS DOS RACIONAIS 1. Racionais não Negativos e não nulos (Q*+): Q*+ = {Z*+} {Todos os números fracionários não negativos} 2. Racionais não Positivos e não nulos (Q*-): Q*- = {Z*-} {Todos os números fracionários não Positivos}

SUBCONJUNTOS DOS RACIONAIS 3. Racionais não Negativos (R+): Q+ = {Z+} {Todos os números fracionários não negativos} 4. Racionais não Positivos (Q-): Q- = {Z-} {Todos os números fracionários não Positivos}

2, 252 Número Racional. Finitos algarismos após a vírgula. 2, 252525. . . Número Racional. Infinitos algarismos periódicos após a vírgula (dízima periódica). 3, 1415926. . . Não é um número Racional. Infinitos algarismos aleatórios após a vírgula

NÚMEROS IRRACIONAIS Como descrever números que não são inteiros nem fracionários?

O "IRRACIONAIS“ é formado por todos os números que NÃO podem ser representados por uma fração de números inteiros. I = {Todos os números que Q não consegue descrever}

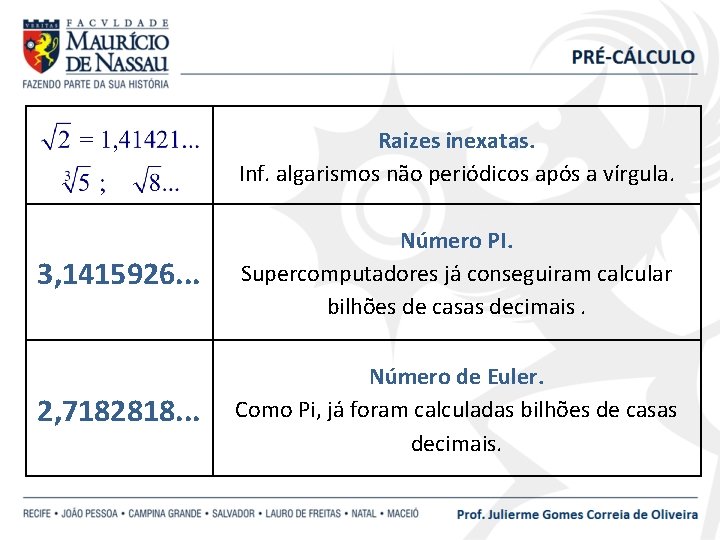
Raizes inexatas. Inf. algarismos não periódicos após a vírgula. 3, 1415926. . . Número PI. Supercomputadores já conseguiram calcular bilhões de casas decimais. 2, 7182818. . . Número de Euler. Como Pi, já foram calculadas bilhões de casas decimais.

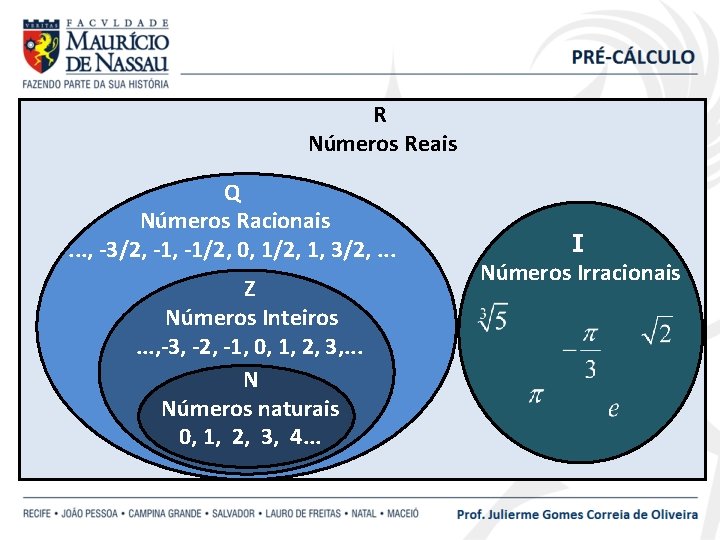
NÚMEROS REAIS “Descreve todo o conjunto dos números racionais e irracionais” R={Q} {I}

R Números Reais Q Números Racionais. . . , -3/2, -1/2, 0, 1/2, 1, 3/2, . . . Z Números Inteiros. . . , -3, -2, -1, 0, 1, 2, 3, . . . N Números naturais 0, 1, 2, 3, 4. . . I Números Irracionais

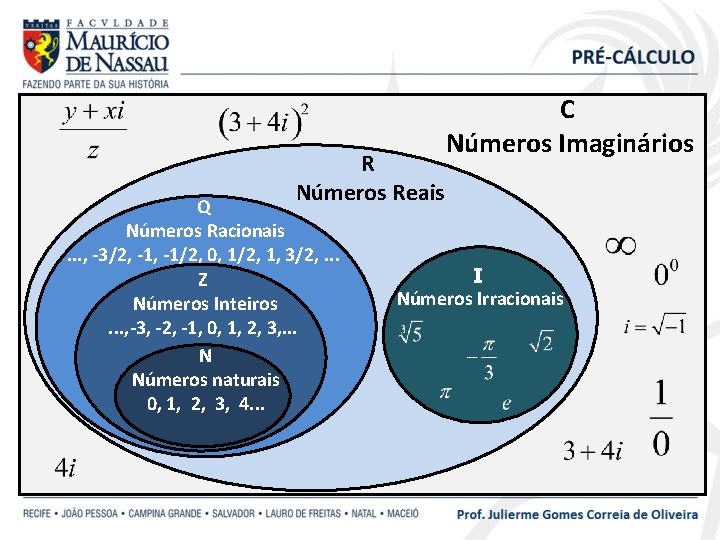
NÚMEROS IMAGINÁRIOS “Descreve todo o conjunto dos números reais e números complexos”

R Números Reais Q Números Racionais. . . , -3/2, -1/2, 0, 1/2, 1, 3/2, . . . Z Números Inteiros. . . , -3, -2, -1, 0, 1, 2, 3, . . . N Números naturais 0, 1, 2, 3, 4. . . C Números Imaginários I Números Irracionais

Axiomas “Um axioma é uma sentença ou proposição que não é provada ou demonstrada, é considerada como óbvia, um consenso inicial necessário para a construção ou aceitação de uma teoria!”

Axiomas para os números Reais 1. Toda e qualquer subtração, na verdade, é uma soma, ou seja: a – b = a + (– b) 2. Toda e qualquer divisão, na verdade, é uma multiplicação, ou seja: ( ) 1 a b = a ÷ b = a· b

Axiomas para os números Reais 3. Lei de Fechamento: A soma a+b e o produto a·b de dois números reais são únicos. 4. Lei Comutativa: a) a + b = b + a b) a·b = b·a “A ordem na adição e na multiplicação é irrelevante!”

Axiomas para os números Reais 5. Lei Comutativa: a) a + (b + c) = (a + b) + c = (a + c ) + b = a + b +c b) (a·b)·c = a·(b·c) = b·(a·c) = a·b·c “A ordem em adições e multiplicações sucessivas é irrelevante!”

Axiomas para os números Reais 6. Lei Distributiva: a) a·(b + c) = a·b + a·c b) b·(a + c) = b·a + b·c c) c·(a + b) = c·a + c·b “A multiplicação é distributiva em relação a adição!”

Axiomas para os números Reais 7. Lei de Identidade: a) Existe apenas um número real na qual a soma dele com outro número qualquer X é igual a X, ou seja: X+0 = 0+X = X b) Existe apenas um número real na qual a multiplicação dele com outro número qualquer x é igual a x, ou seja: 1·X = X· 1 = X

Axiomas para os números Reais 8. Lei de Inverso: a) Para qualquer número Real X existe um Real – X, tal que: X + (–X) = (–X) + X = 0 b) Para qualquer número Real X ≠ 0, existe um número real X 1 tal que: X·(X-1) = (X-1)·X = 1

Axiomas para os números Reais 9. Lei do fator zero: a) Para qualquer número Real X: X· 0 = 0 b) Se X e Y são dois números reais tal que X·Y = 0, então obrigatoriamente X = 0 ou Y = 0.

Axiomas para os números Reais 10. Lei do número negativo: a) (– 1)·a = – a b) (– 1)·(–a) = – (–a) = a c) (–a)·(–b) = a·b d) –ab = (–a)·b = a·(–b) = – (–a)·(–b)

Axiomas para os números Reais 11. Lei dos Quocientes:

Axiomas para os números Reais 12. Lei do número absoluto: Qualquer número Real tem um número absoluto correspondente, tal que: Se a < 0, ou seja, o negativo de a, | – a | = a Se a > 0, ou seja, o positivo de a, | a | = a |–a|=|a|=a

Axiomas para os números Reais 13. Lei da ordem das operações: “Em uma expressão, uma soma ou uma subtração só deve ser realizada após todas as operações de multiplicação e divisão já terem sido efetuadas, ao menos que elas apareçam isoladas por ( ), [ ] ou { }”.
 Cadeias industriais e os recursos naturais
Cadeias industriais e os recursos naturais Sean a y b conjuntos no vacios
Sean a y b conjuntos no vacios Cardinalidade dos conjuntos
Cardinalidade dos conjuntos Soma dos conjuntos
Soma dos conjuntos Conjuntos numéricos símbolos
Conjuntos numéricos símbolos Correspondencia multiple para niños
Correspondencia multiple para niños Producto cartesiano de dos conjuntos
Producto cartesiano de dos conjuntos Numero romano ivx
Numero romano ivx Nmeros reales
Nmeros reales Nmeros primos
Nmeros primos Ejercicios de números romanos para imprimir
Ejercicios de números romanos para imprimir Nmeros reales
Nmeros reales Nmeros romanos
Nmeros romanos Nmeros enteros
Nmeros enteros Nmeros enteros
Nmeros enteros Nmeros naturales
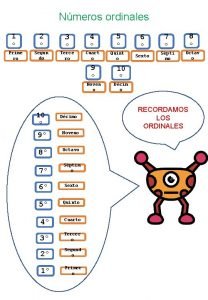
Nmeros naturales Nmeros ordinales
Nmeros ordinales Nmeros enteros
Nmeros enteros Nmeros
Nmeros Nmeros ordinales
Nmeros ordinales Quadrada de 7
Quadrada de 7 Nmeros ordinales
Nmeros ordinales Numeros pentagonales
Numeros pentagonales Nmeros ordinales
Nmeros ordinales Los números romanos
Los números romanos Nmeros naturales
Nmeros naturales Primero tercero cuarto quinto
Primero tercero cuarto quinto Yu chi ho
Yu chi ho Number line
Number line Rios europeus
Rios europeus Piramide asiatica
Piramide asiatica Atributos morais e naturais de deus
Atributos morais e naturais de deus